基于功率损失指数的配电网无功补偿装置两阶段多目标优化配置方法研究∗

郭 挺 陈中豪 徐良德 杨 帆

(1.广东电网有限责任公司广州供电局 广州 510600；2.广州电力设计院有限公司 广州 510610)

1 引言

随着我国电网建设速度的加快与规模的逐步扩大，配电网网络损耗、电压水平、功率因数等问题越来越多地引起运行人员的关注[1-6]，很多学者开展了相应治理措施的研究，主要治理方法涉及利用分布式电源、网络重构和无功补偿装置配置等[7-11]。在馈线上安装以电容器为代表的无功补偿装置既可以提高功率因数，还可以改善电压分布和减少功率损失。考虑到装置成本和维护费用，目前的重点是开展配电网无功补偿装置的优化配置方法研究。

无功补偿装置配置优化问题所考虑的重点是目标函数的构建和优化求解方法的设计。文献[12]采用了改进粒子群算法，对考虑系统电压偏移总量与有功损耗最小的无功优化问题进行求解，但未考虑装置的成本。文献[13]基于和声搜索算法实现配网电容器的多目标优化配置，从而在降低网损的同时最小化无功补偿费用。文献[14]引入反向学习对鸡群算法进行改进，从而提升了配电网无功优化模型的整体性能，但该方法耗时较长。文献[15]采用粒子群算法求解城市配电网无功优化配置问题，模型目标函数为运行成本的期望值最小，但未开展安装节点的选取，同时求解耗时较长。文献[16]提出了鲸鱼优化算法对以有功损耗最小为目标的无功配置优化问题进行求解，但目标函数较为单一，易于陷入局部最优。此外未综合考虑关键节点的优先选择。文献[17]将布谷鸟算法中的飞行和淘汰机制引入粒子群算法，对以有功损耗最小为目标的无功优化配置问题进行求解，但目标函数过于单一，所得结果不完全符合配电网实际运行。文献[18]考虑含分布式电源的接入，提出了基于模糊聚类下的混沌优化人工鱼群算法，对以网损最小为目标的无功优化配置问题进行建模求解。文献[19]利用改进教与学算法，实现以有功网损和电压偏离度最小为综合目标的无功优化配置。

上述优化方法可实现无功补偿装置位置与容量的优化配置，但总体而言设计的目标函数较为单一，对关键节点的优选考虑不足，优化求解方法易陷入局部最优。为此，本文提出了计及功率损失指数的配电网两阶段无功补偿多目标优化配置方法。首先利用功率损失指数进行无功补偿装置安装节点的优先选取；其次以有功损耗相应的损失、装置购买费用、安装费用以及运行费用最小化为综合目标函数，引入罚函数并建立了计及功率损失指数的无功补偿装置多目标优化配置模型，应用䲟鱼优化算法进行模型求解，得到不同负荷条件且已有分布式电源接入的配电网无功补偿装置的最佳安装位置和容量，通过在IEEE-34 及PG-69 节点系统中的算例验证了所提方法的有效性和性能优势。

2 基于功率损失指数的候选节点选取

采用图1 所示网络模型进行配电网功率损耗的计算。

图1 含无功装置配电网损耗计算模型

节点i与下游节点j之间线路的有功损耗∆Pij和无功损耗∆Qij的计算方法为

式中，为节点j电压矢量；Rij、Xij分别为节点i与j之间线路的电阻和电抗；Pi、Qi分别为上游馈线注入节点i的有功、无功功率。

在节点j接入无功补偿装置后，线路有功损耗将减少。本文提出基于功率损失指数来初选无功补偿装置的安装位置。该方法对每个母线节点(首端母线节点除外)注入无功功率，并进行潮流计算，对比有功功率损耗的变化，最后选取具有较大功率损失指数的母线节点作为无功补偿装置的优先配置位置。功率损失指数定义为

式中，Pl(j)为母线节点j处安装无功补偿装置引起的有功损耗减少值；Plmin=min{Pl(j)} ，Plmax=max{Pl(j)},j=2,…,n，其中n为配电网节点总数，首节点编号为1。

3 无功补偿装置优化配置模型

3.1 目标函数

无功补偿装置优化配置模型的目标为最小化总成本费用，包括有功损耗相应的电价损失f1、安装费用f2、购置费用f3以及运行费用f4，同时加入对节点电压、总有功损耗越限的罚函数，如式(3)所示

式中，α为电价(元/kW·h)；PLoss为总有功损耗；T=8 760 h；β为折旧系数；CI为无功补偿装置的安装费用(元/台)；k为装置总安装台数。Ca为电容器的购买费用(元/kVar)；QCi为注入的无功功率值(kVar)；χ为运行成本(元/台)；λ1为电压越限惩罚系数；ΔUi为节点电越限值；Uimin、Uimax分别为节点电压最小值、最大值；λ2为总有功损耗越限惩罚系数；ΔP为总有功损耗越限值。

PLoss计算方法为

式中，Rd、Xd为支路d的电阻、电抗；L为支路总数；Ui、Uj分别为母线i、j的电压。

节点电压越限值的计算方法为

总有功损耗越限值的计算方法为

3.2 约束条件

(1) 无功补偿容量约束。节点安装的无功补偿装置容量应满足

式中，QCmin、QCmax分别为无功补偿装置容量的最小值、最大值。

(2) 潮流约束。系统有功和无功功率需要满足如下平衡约束

式中，PS、QS分别为系统有功功率、无功功率；PLineloss(i)、QLineloss(i)分别为支路i的有功损耗、无功损耗；PLoad(e)、QLoad(e)分别为节点e负荷的有功功率、无功功率；QC(r)为第r台无功补偿装置的容量。

(3) 无功功率约束。总无功补偿装置容量不超过无功负荷的75%

(4) 功率因数约束。电网的功率因数必须满足以下约束

式中，PF(i)为节点i的功率因数值；PFmin、PFmax分别为该节点功率因数的最小值、最大值。

(5) 线路最大容量约束。线路的容量应低于其限值

式中，SLine(i)、SLineR分别为线路i的容量及额定容量。

3.3 䲟鱼优化算法建模分析

本文采用䲟鱼优化算法求解所建立的无功补偿装置多目标优化配置模型，无功补偿优化配置的位置与容量的求解可以看作䲟鱼在海里捕食的过程。该算法模拟䲟鱼在海洋中的生物特性，具备搜索速度快、可获得全局最优解等优点[20]。图2 展示了䲟鱼算法的融合框架，通过在两种宿主之间切换，创建了一种新的算法融合，该融合框架包含探索和开发两种运动模式，模式之间的切换通过自创的“逐步试”实现。在探索阶段提出的“䲟鱼因子”，能够实现提高优化精度，使算法有效收敛。

图2 䲟鱼算法的融合框架模型

3.3.1 初始化

假设候选解为䲟鱼，其在搜索空间中的位置O是问题变量。䲟鱼的当前位置记为Ox=(Ox1，Ox2，…，Oxm)，其中x为䲟鱼的数量，m为其搜索空间的维数，另外，OB=(O1*，O2*，…，Om*)代 表 其 食 物(目标)，也是算法中的最优解。在该算法中，每个候选解应该有对应的适应度函数。通常适应度函数表示为y(Ox)=y(Ox1，Ox2，…，Oxm)，而y(OB)=y(O1*，O2*，…，)表示最优䲟鱼位置对应的最佳适应度值。

3.3.2 全局勘探

当䲟鱼附着在旗鱼上，基于旗鱼优化算法的精英思想，䲟鱼的改进位置更新如式(12)所示

式中，为在迭代次数t时䲟鱼的最佳位置；为在迭代次数t时䲟鱼的随机位置。

式(12)既保证了最优个体引导更新，同时又增加䲟鱼的随机选择，保证了搜索空间的探索性。

为了确定䲟鱼更换宿主与否，其必须在宿主附近不断尝试小幅度移动，建模公式如下

式中，为迭代次数t-1 时的位置；为迭代次数t时试探性步骤的位置；randn为䲟鱼随机的全局小步长。

在该步骤之后，还需要进一步判断两个位置的适应度值的大小来决定是否更换宿主。

3.3.3 局部开发

当䲟鱼附着在鲸鱼上时，基于鲸鱼优化算法推导了䲟鱼的位置更新公式如下

式中，G为猎人与猎物之间的距离(当前最优解)；δ为[-1，1]的随机数；w在[-2，-1]之间线性下降；T为最大迭代次数。

由于鱼群的聚集性不是时时都很强，所以䲟鱼会在宿主嘴边捡漏，当䲟鱼在宿主旁游行，其数学公式如下

式中，E为与䲟鱼空间维数相关的移动步长；V为䲟鱼因子，表示䲟鱼占据宿主体积的大小，其取值范围一般在[0，0.3]。图3 为V=0.1 条件下的宿主取食模型。

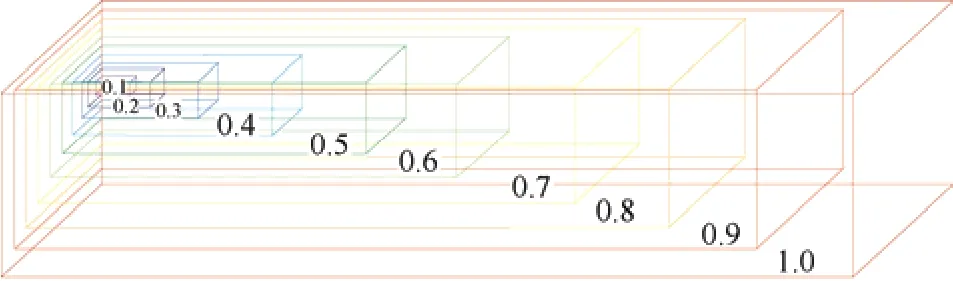
图3 宿主取食模型

4 基于䲟鱼优化算法优化模型求解

本文设计的计及功率损失指数的电网两阶段无功补偿多目标优化配置方法，流程如图4 所示。具体步骤如下所示。

图4 电网两阶段无功补偿装置多目标优化流程

步骤1：进行电网基本资料收资，并搭建电网基本模型。

步骤2：针对电网的初始状态进行潮流计算，并根据式(2)计算功率损失指数，确认无功补偿装置的关键母线节点。

步骤3：将步骤2 中的关键母线节点作为无功补偿位置默认值输入到优化代码中，并确定䲟鱼优化算法的最大迭代次数和数量等参数。

步骤4：设定每个䲟鱼在其允许范围内为优化算法中的变量向量X=[位置，容量]，在约束条件下由每个䲟鱼(一组优化变量)代入式(3)来计算目标函数的总成本费用。

步骤5：根据式(13)、式(14)更新䲟鱼的数量。

步骤6：对更新后的数量执行潮流计算，并更新目标函数的计算。若该步骤的目标函数值小于步骤4，则将更新后的目标函数计算值替换原来的计算值。

步骤7：若满足收敛条件则执行下一步，输出费用最低的最优变量，否则返回继续执行步骤5。

5 算例分析

本文选用IEEE-34 和PG-69 配电网为目标系统开展所提方法性能的验证，两个配电网的拓扑如图5 所示。IEEE-34 系统的基准电压为11 kV，总负荷4.636 5(MW)+j2.873 5(MVar)。PG-69 系统的基准电压为12.66 kV，总负荷3.802 19(MW)+j2.694 6(MVar)。表1 给出了无功优化装置的基本信息。

表1 无功补偿装置基本参数

图5 配电网拓扑结构

5.1 基础仿真分析

以IEEE-34 和PG-69 配电网未进行任何无功补偿时的状态为基础，相应的潮流计算可知两者有功网速分别为221.72 kW 和226.47 kW，节点电压分布如图6 所示。由图6a 可知，IEEE-34 节点系统最小电压为节点27 的0.941 6 p.u.，由图6b 可知PG-69节点系统的最小电压为节点54 的0.908 9 p.u.。

图6 配电网节点电压分布

对两个配电网的功率损失指数进行计算，结果如图7 所示。由图7a 可知，IEEE-34 节点系统中无功配置优选位置为节点26、25、24、23、22、21和20；由图7b 可知，IEEE-69 节点系统无功配置优选位置为节点54、53、52、51、50、49 和48。

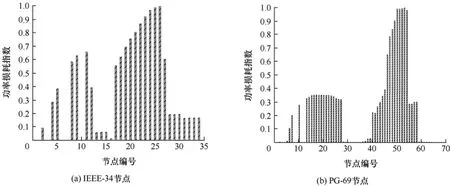
图7 配电网功率损失指数

5.2 算法性能分析

对IEEE-34 和PG-69 节点系统无补偿、仅采用䲟鱼优化算法的无功优化配置和计及功率损失指数+䲟鱼优化算法的无功优化配置结果进行对比(算法中种群数为50，最大迭代次数为500)，结果如表2 所示，迭代过程及节点电压分布对比如图8 和图9 所示。

表2 三种情况下无功优化配置结果对比

图8 计及功率损失指数的优化迭代曲线

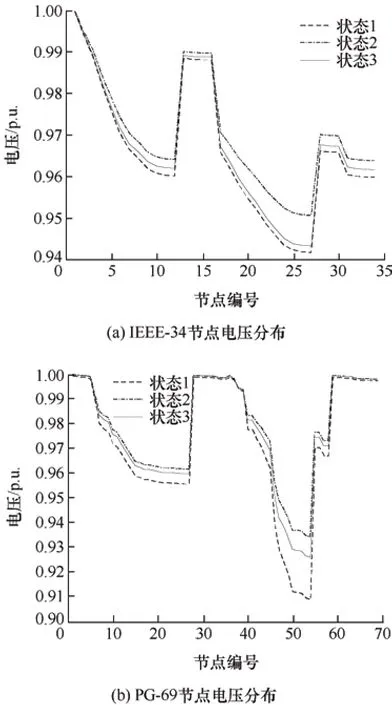
图9 计及功率损失指数的节点电压分布对比

由表2 可知，对于IEEE-34 节点系统，与未考虑功率损失指数和不进行无功补偿相比，采用本文方法时系统有功损耗分别减小了2.52%和23.54%，最小电压值分别提升了0.25%和0.95%，优化配置成本费用节省了0.07%和14.9%。考虑功率损失指数后，优化求解时间可减少29.05%，但优化结果的电容器费用增加了3.78%。

对于PG-69 节点系统，与未考虑功率损失指数和不进行无功补偿相比，采用本文方法时网络有功损耗分别减小了1.95%和32.19%，最小电压值提升了0.44%和2.51%，优化配置成本费用节省了0.22%和25.56%；考虑功率损失指数后，优化求解时间可减少17.08%，电容器费用增加0.13%。

分析图8 可知，IEEE-34/PG-69 节点系统采用本文无功优化配置方法时，迭代过程算法适应度在迭代次数为 20 次/19 次时收敛，获得最优解82 620.69 元/73 839.15 元，比仅利用䲟鱼优化算法的求解过程快。图9 表明，本文无功优化配置方法可获得整体最佳的节点电压分布，相较于仅利用䲟鱼优化算法更能均衡提升各节点电压。

为进一步体现本文优化算法的优势，将䲟鱼优化算法(以下简称方法1)与粒子群优化算法(以下简称方法2)和鲸鱼优化算法(以下简称方法3)进行性能指标的对比，结果如表3 所示，三种方法下迭代曲线及节点电压分布的对比如图10 和图11 所示。

表3 不同优化算法下的无功优化配置结果对比

图10 不同优化方法下的迭代曲线

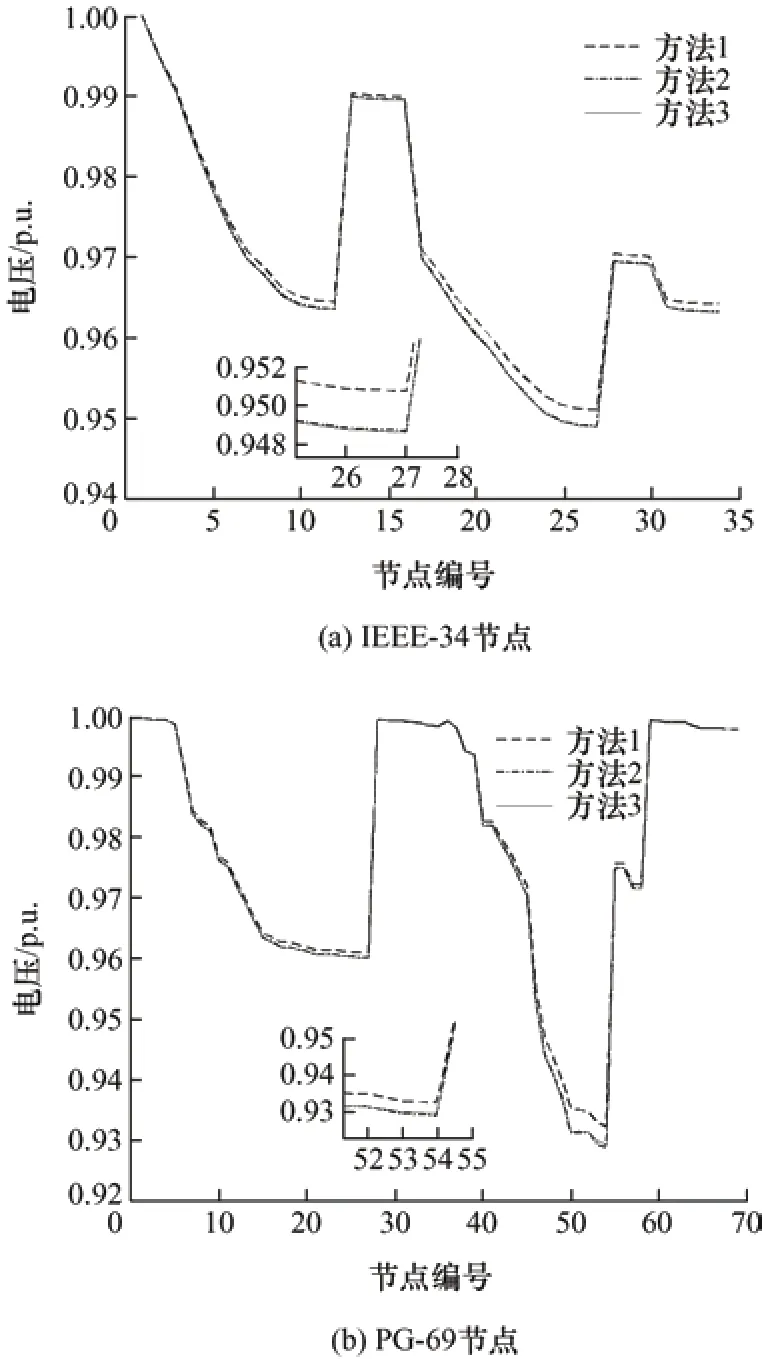
图11 不同优化方法下节点电压分布

由表3 可知，对IEEE-34/PG-69 节点系统，方法1 所得有功损耗较(方法2、方法3)分别减小了(0.34%、1.15%)/(0.72%、0.55%)，最小电压值提升了(0.22%、0.22%)/(0.39%、0.32%)。

对两个配电网，方法1 下的优化配置成本费用较(方法2、方法3)节省了(1.09%、0.12%)/(0.61%、0.27%)。而电容器相关费用则是方法3 最小，相较于(方法1、方法2)减少(3.97%、15.58%)/(1.98%、2.03%)；对比三种方法的优化均值可知，方法1 的性能优于方法2 及方法3，比后两者分别小了(1.07%、0.13%)/(0.69%、0.35%)。

由图10 可知，对IEEE-34/PG-69 节点系统，方法1 求解适应度值在迭代次数为20 次/19 次时即收敛，得到最优值82 620.69 元/73 839.15元；方法3 适应度值在迭代次数为41 次/40 次时得到最优值82 723.8 元/74 038.84 元，而方法2 的适应度值在迭代次数为10 次/15 次时获得最优值83 523.92 元/74 293.27 元。就优化求解时间而言则是方法2 最好，相较于(方法1、方法 3)减少了(34.92%、38.01%)/(23.63%、27.41%)。图11 表明，基于䲟鱼优化算法的无功优化配置整体节点电压分布最佳，而粒子群优化算法与鲸鱼优化算法提升的效果几乎相当。

因此，通过计及功率损失指数并采用䲟鱼优化算法求解多目标无功补偿装置优化配置问题将具有最佳综合性能。

5.3 负荷水平的影响分析

为进一步研究不同负荷条件下本文算法性能，将IEEE-34 和PG-69 节点系统的有功负荷乘以相应系数以模拟不同负荷条件。图12 给出了不同负荷条件下Pl(j)的最大值。

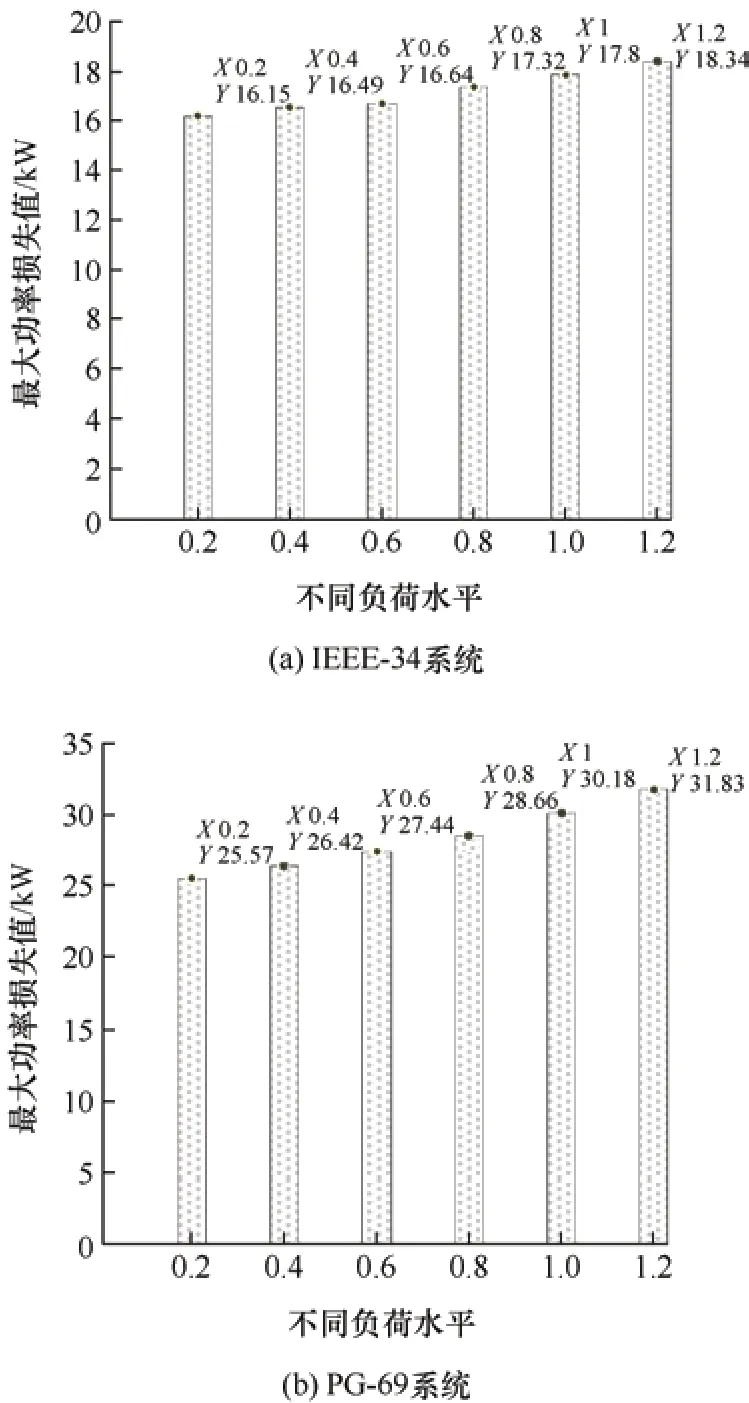
图12 不同负荷水平下最大功率损失值

由图12 可知，对两个不同的配电网，负荷水平越高所得Pl(j)的最大值越大，两者呈正相关，即高负荷水平下配电网更需要开展无功补偿。对IEEE-34 和PG-69 节点系统均设置3 种不同负荷水平，结果如表4 所示。

表4 不同负荷条件下的无功优化配置结果

由表4 可知，对不同规模配电网，不同负荷水平对无功补偿装置的选址均将产生影响。负荷水平降低时，有功损耗会减少、功补偿配置容量、成本费用、电容器费用、优化求解时间均减少，而系统最小电压提高。其中，IEEE34/PG-69 节点系统在负荷系数(0.6、0.8)下比负荷系数1 下的有功损耗减少了(34.37%、71.95%)/(34.59%、60.65%)，成本费用减少了(31.07%、65.66%)/(32.59%、57.04%)，最小电压值提升了(0.92%、2.79%)/(2.10%、2.39%)，电容器费用减少了(4.80%、5.54%)/(1.96%、12.36%)，优化时间减少了(4.15%、8.87%)/(3.28%、4.27%)，系统负载水平的增加一定程度上将导致无功补偿容量及其相应成本的增加。

5.4 DG 接入的影响分析

设定IEEE-34 和PG-69 节点系统分别接入1 个和2 个DG，接入位置及容量如表5 所示。DG 接入下的系统功率损失指数如图13 所示，无功优化配置结果对比如表6 所示，相应迭代曲线及节点电压分布的对比如图14 和图15 所示。

表5 DG 接入信息

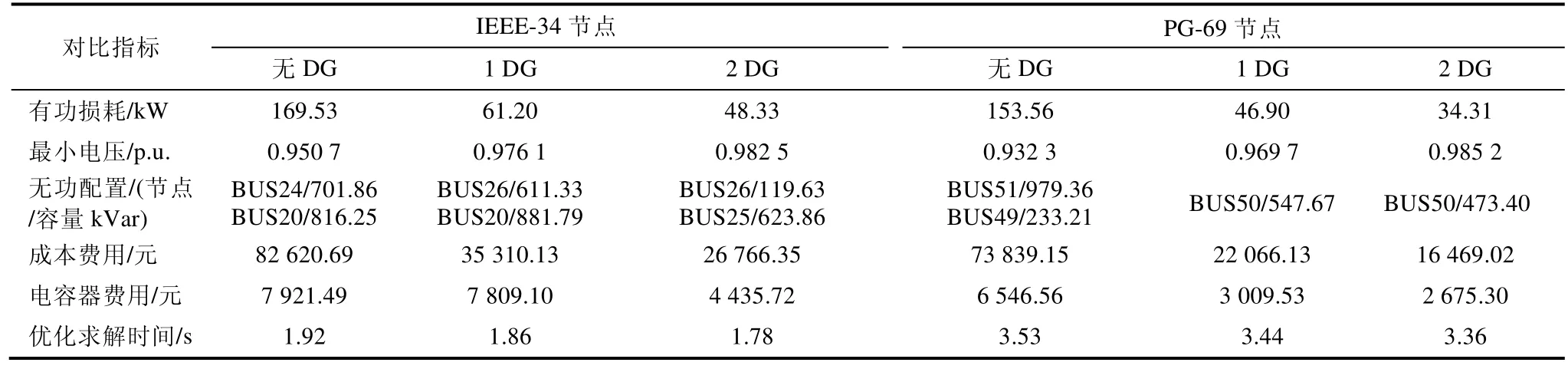
表6 DG 接入后的无功优化配置对比

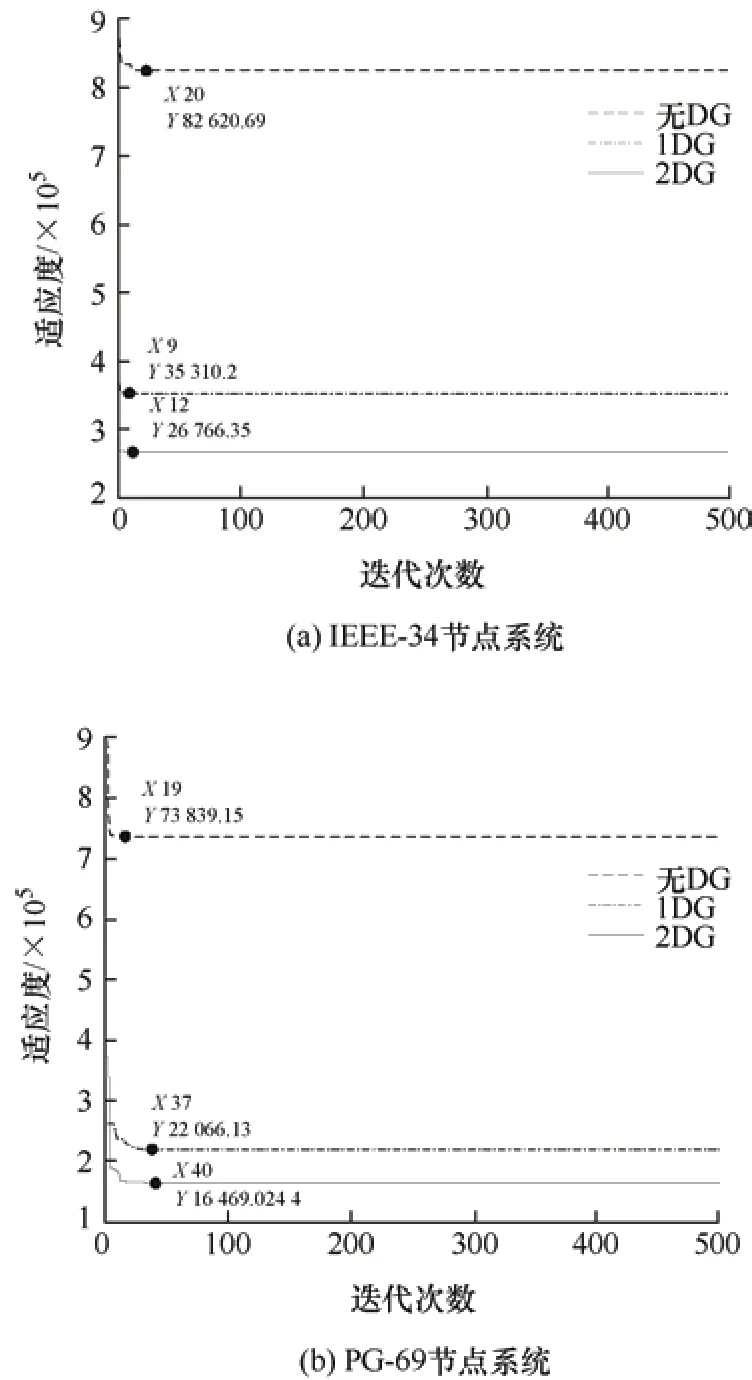
图14 DG 接入下的优化迭代曲线对比

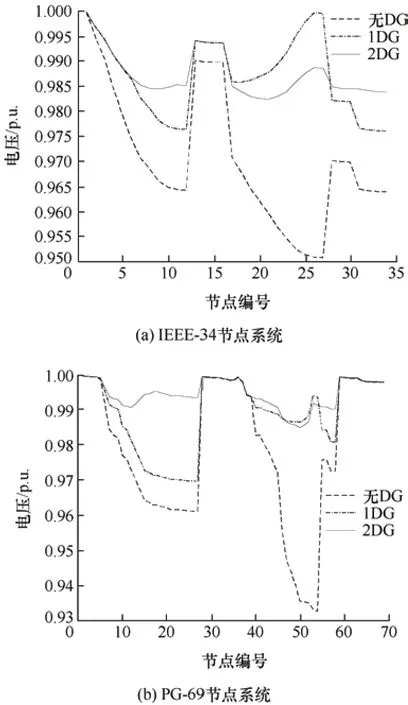
图15 DG 接入下的节点电压分布对比

由图13 可知，DG 的接入将对配电网系统的功率损失指数产生一定影响，2 个DG 接入下的功率损失指数略小于1 个DG 接入下的情况，但关键节点保持不变：对IEEE-34 节点系统为26、25、24、23、22、21、20，对PG-69 节点系统为54、53、52、51、50、49、48。

如表6 所示，在已有DG 接入时IEEE-34/PG-69节点系统所需无功配置容量均减少，且DG 接入越多无功配置容量可降低更多，最大可达51.02%/60.95%；接入(1 个、2 个)DG 时，两个配电网有功损耗值减少达(63.90%、71.49%)/(69.45%、77.65%)，相应成本费用减少(57.62%、67.60%)/ (70.11%、77.69%)，最小电压分别从0.950 7 p.u./ 0.932 3 p.u.升至(0.976 1 p.u.、0.982 5 p.u.)/ (0.969 7 p.u.、0.985 2 p.u.)。

由图14 可知，IEEE-34/PG-69 系统接入1 个DG 时，算法适应度值在迭代次数为9 次/37 次时可获得最优值35 310.13 元/22 066.13 元，而2 个DG接入时的适应度值在迭代次数为12 次/40 次时可获得最优值26 766.35 元/16 469.02 元。图15 表明，2个DG 接入后的系统无功优化配置整体节点电压分布最优。因此，充分利用DG 的接入开展无功补偿装置的优化配置可进一步提升配电网运行性能，同时节省安装无功补偿装置的成本费用。

6 结论

本文提出了计及功率损失指数的电网两阶段无功补偿多目标优化配置方法，并通过基于IEEE-34及PG-69 节点的算例进行了仿真验证，算例结果表明如下结论。

(1) 计及功率损失指数的方法可优先对候选出的关键节点进行补偿，减少了搜索空间规模，优化配置效果整体优于未考虑功率损失指数的情况。

(2) 计及功率损失指数的䲟鱼优化算法可以更好均衡优化配置的多个目标，相比常规粒子群算法及鲸鱼优化算法，可更好获取多目标优化问题的全局最优解，解决了传统优化算法易陷入局部最优的问题，提高了无功补偿多目标优化配置的准确性及适用性。

(3) 所提方法能够适应负荷水平的变化和分布式电源的接入。充分利用DG 的接入开展无功补偿装置的优化配置可进一步提升配电网运行性能，同时节省所需无功补偿装置的相关费用。