基于新型滑模控制和STSM-MRAS观测器的SPMSM转速估计研究
段乾超,李玉东,2,孟娟娟
(1.河南理工大学 a.电气工程与自动化学院 b.继续教育学院,河南 焦作 454003;2.河南省煤矿装备智能检测与控制重点实验室,河南 焦作 454003)
0 引言
永 磁 同 步 电 机( Permanent Magnet Synchronous Motor, PMSM )由于响应速度快、体积小、效率高以及功率密度高等优点,在航空航天、工业、船舶电力推动器等领域应用广泛[1-2]。PMSM 作为一个强耦合、非线性、多变量的系统,在受到内部以及扰动因素影响时,传统PI 速度控制无法满足PMSM 高性能控制要求。因此,国内外学者提出了许多控制策略,例如,模糊滑模速度控制[3]、滑模速度控制[4]、滑模自抗扰速度控制[5]等。其中,滑模速度控制具有强鲁棒性,响应迅速,对参数变化及扰动不敏感等优点,但是其在稳态运行时存在抖振问题[6-7]。为了削弱抖振现象,文献[8]提出了模糊滑模速度控制,该方法对于系统被控对象不敏感,但很大程度上依赖于专家控制的经验。文献[9]引入了非奇异快速终端滑模速度控制,缓解了滑模速度控制的抖振问题,但是当系统偏离平衡点时,存在收敛速度较慢的问题。
在实际工程中,PMSM 高性能控制策略的实现依赖于对转子位置和转速的精确测量。随着电机在不同工作环境中的应用,位置传感器的使用会降低系统的可靠性,导致无法精确测量电机的转速和转子位置[10-11]。因此,无位置传感器技术具有重要的研究意义。目前,无位置传感器控制策略包括:(1)滑模观测器法[12-13],这种策略具有高鲁棒性和高动态性,但是其固有的滑模抖振问题会降低估计精度。文献[14]提出了改进滑模观测器,利用新型函数构建趋近律,减小了传统滑模观测器的抖振现象。(2)扩展卡尔曼滤波法[15-16],该方法减小了噪声对观测器的不利影响,但是其计算过程较为复杂。文献[17]提出了降阶的扩展卡尔曼滤波器法,减小了运算量,提高了运算速度。(3)模型参考自适应算法[18-19],该方法估计精度高,控制算法简单,在中高速运行时性能较好,应用较为广泛。文献[20]利用MRAS 观测器对同步磁阻电机进行无位置传感器控制,传统MRAS 观测器的自适应机构可以看作PI 控制器,其鲁棒性不强,动态性能较差,当发生负载扰动时,其估算精度将会降低。
针对滑模速度控制策略和传统MRAS 估计策略的不足,本文提出了一种基于全局快速终端滑模控制器(Global Fast Terminal Sliding Mode Controller,GFTSMC) 和 超 螺旋滑模MRAS(Super-Twisting Sliding Mode MRAS,STSM-MRAS)观测器的SPMSM 转速估计策略。首先,结合线性滑动模态和快速滑动模态构建新型滑模面,设计全局快速终端滑模控制器,使系统状态误差能在有限时间内快速收敛到零。其次,在传统MRAS 观测器的基础上引入超螺旋滑模算法,构建超螺旋滑模MRAS 观测器模型,通过高阶符号函数获取电机的转速和转子位置,缓解了滑模控制固有的抖振问题,提高了系统的鲁棒性。最后,经过仿真实验对比,验证了本文所提估计策略的可行性与有效性。
1 SPMSM数学模型
在d-q 轴坐标系下,忽略系统阻尼的影响,SPMSM 的数学模型为:
式中,id、iq和ud、uq为d 轴、q 轴的定子电流和电压;R、Ls为定子电阻和电感;ω为电机转速;φf为永磁体磁链;p为极对数;TL为负载转矩;J为转动惯量。
2 控制器设计
2.1 传统滑模观测器
定义PMSM 的状态变量:
式中, 为电机给定转速。
结合SPMSM 的数学模型,对式(2)求导可得,
选取滑模面函数为:
式中,c>0 为待设计参数。
对式(5)求导,可得:
根据指数趋近律法,可得滑模控制器表达式为:
式中,ε>0,q>0。
从而可得q 轴参考电流为
根据滑模到达条件 <0,可验证系统在滑模控制下是渐近稳定的。
2.2 GFTSMC控制器
传统滑模控制通常采用线性滑模面,系统状态误差渐近收敛至零,但收敛时间却趋于无穷。为此,国内外学者提出了快速终端滑模控制策略,使状态误差能够在有限时间内收敛至零,但是其收敛速度比线性滑模的收敛速度慢。
为保证系统状态误差能够在有限时间内快速收敛到零,结合线性和快速滑动模态,设计了全局快速终端滑动模态。其滑模面函数为[21]:
式中,α>0,β>0,b>a>0 且为奇数。
当系统状态x1偏离平衡点时,收敛时间由决定,反之,则由决定。
全局快速终端滑模控制器表达式为:
其中,α>0,β>0 ,ρ>0,µ>0,a、b、c、d(a>b及c>d)为正奇数。由于GFTSMC控制律是连续的,不含切换项,因此可有效削弱抖振现象。
由式(4)和式(10)可得q 轴参考电流:
由式(11)可得,在全局快速终端滑模控制下,电机转速误差能够沿着滑模面到达系统稳定点。
为 证 明GFTSMC 的 稳 定 性, 构 建Lyapunov 函数
对式(12)求导,整理可得
式(13)中,ρ>0,µ>0,且c、d为正奇数,则 。因此,该控制器满足Lyapunov 稳定性定理[22]的条件,符合滑模存在和全局到达条件。
3 观测器设计
3.1 传统MRAS观测器
传统MRAS 的辨识原理如图1 所示,包含参考模型、可调模型和自适应律模型。
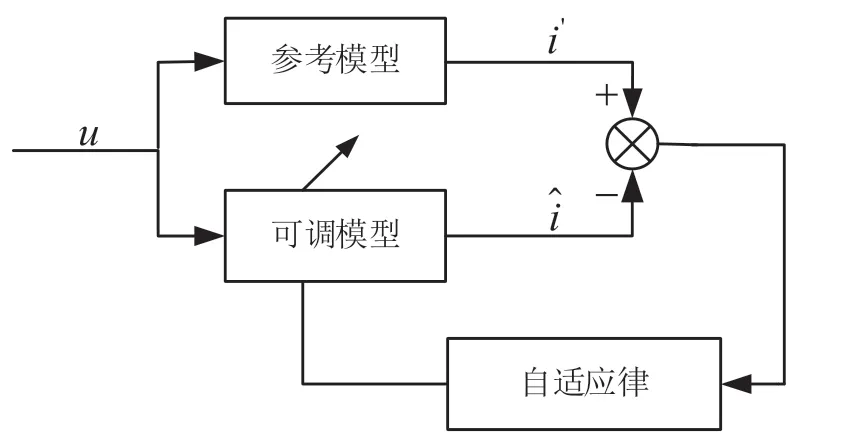
图1 MRAS辨识原理图
从式(1)中分析可知,SPMSM 的数学模型中包含待辨识的转速信息参数,因此可构建可调模型。
将式(1)变换,可得:
式中:
将电流估计值 和转速估计值 代入式(14),可得可调模型:
整理上式,可得误差状态方程为:
将上式用状态空间方程表示,可得:
式中:
进一步整理,可得:
其中,c为单位矩阵。
式(16)描述的系统是一个非线性时变系统,适用于Popov 超稳定性原理。根据Popov 超稳定性原理,非线性时变系统稳定的充要条件为[23]:
对于条件(1),根据正实引理[24]可证明该条件成立。
对于条件(2),需满足:
对式(19)进行逆向求解可得转速估计的自适应律:
结合式(14)和式(20),可得估算转速表达式为:
由式(20)可知,MRAS 的自适应律可以看作PI 控制器。结合图1 可知,当参考模型的输出电流与可调模型的输出电流误差收敛到零时,此时电机的估计转速将达到电机的实际转速。
3.2 超螺旋滑模MRAS观测器
为解决PI 自适应模型鲁棒性差以及滑模控制固有的抖振问题,本文引入超螺旋滑模控制策略替代传统MRAS 观测器的PI 自适应律[25]。其表达式如下:
式中,x1和x2是状态变量;x˙1 和x˙2 是对应状态变量的导数;k1和k2为滑模增益;sign()为符号函数。
由式(22)可以看出,sign()是非连续函数,这将会引起滑模控制的抖振问题。超螺旋滑模算法是二阶滑模控制,在sign()前引入连续项并将sign()放到高阶导数中,有效缓解了传统滑模的抖振问题。结合式(21),构造滑模面:
利用式(1)和式(15),对式(23)求导,整理可得:
由式(23)和(24)可知,当s=s˙=0 时,参考模型的输出电流id和iq与可调模型的输出电流 和 的误差收敛到零,同时,由观测器得到的估计转速也收敛于电机的实际转速。
根据选取的滑模面s和式(24),基于STSM-MRAS 的估算速度表达式为:
估算转子位置为:
式中, 为转子位置估计值。
3.3 稳定性分析
由Lyapunov 稳定性定理可知,状态矢量为:
其中,ζ1和ζ2是状态变量。由式(27)中可知,当状态变量ζ1和ζ2在有限时间内收敛到零时,那么状态变量x1和x2在有限时间内也能够收敛到零。结合式(22),可得在有限时间内系统状态可以到达滑模面且状态误差收敛到零。
对式(27)进行求导,将式(22)代入,整理可得:
进一步选取Lyapunov 函数为:
对式(18)求导为:
结合式(27),进一步变换,整理可得:
可得:
当滑模增益k1、k2>0 时,可知矩阵A 和B 是正定矩阵,矩阵 为负定矩阵。因此,当满足滑模增益k1、k2>0 时,系统在平衡点ζ1=ζ2=0 是渐近稳定的。
4 仿真实验
为验证基于GFTSMC 和STSM-MRAS 的转速估计策略的可行性与有效性。采用id=0的矢量控制方法,忽略系统阻尼的影响,利用Matlab/Simulink 仿真平台构建SPMSM 无位置传感器控制系统,系统的框图如图2 所示。仿真电机参数如表1 所示。
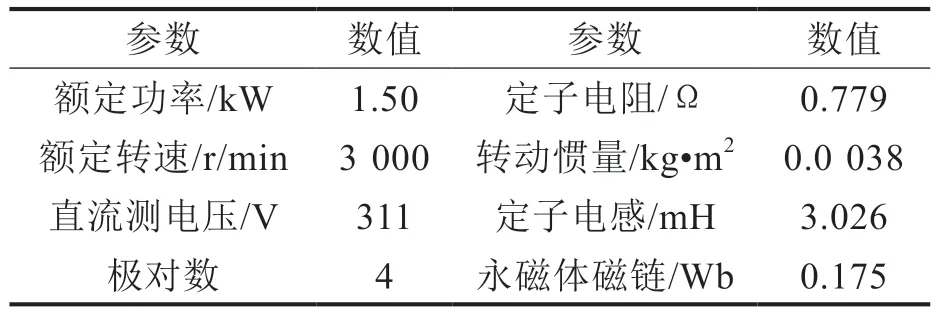
表1 仿真电机参数
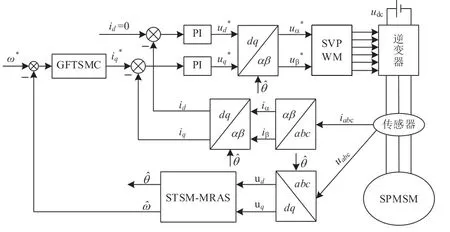
图2 基于GFTSMC和STSM-MRAS的SPMSM无位置传感器控制系统框图
在空载条件下启动,设定电机的初始转速为1 000 r/min,在0.2 s 时,转速突变到2 500 r/min。基于GFTSMC 和STSM-MRAS的转速转速估计策略与基于传统SMC 和MRAS的转速估计策略的仿真结果如图3 所示。

图3 给定转速突变时两种控制策略的实际转速和估计转速的仿真对比图
从图3 中可见,当转速到达1 000 r/min 时,基于传统SMC 和MRAS 的转速估计策略具有较大的超调,最大转速误差为10 r/min,而基于本文所提估计策略能够消除超调,最大转速误差为4 r/min,且达到稳定运行状态的时间比基于传统SMC 和MRAS 的估计策略达到稳定运行状态的时间缩短了0.02 s。当转速突变到2 500 r/min 时,基于传统SMC 和MRAS 的估计策略的转速误差波动较大,收敛到零的时间较长,而本文所提估计策略的转速误差波动较小,经过0.1 s 后逐渐收敛到零。
为验证本文所提估计策略的抗干扰性能。设定电机的初始转速为1 000 r/min,在0.2 s时加入10 N·m 负载。两种转速估计策略的仿真结果如图4 所示。
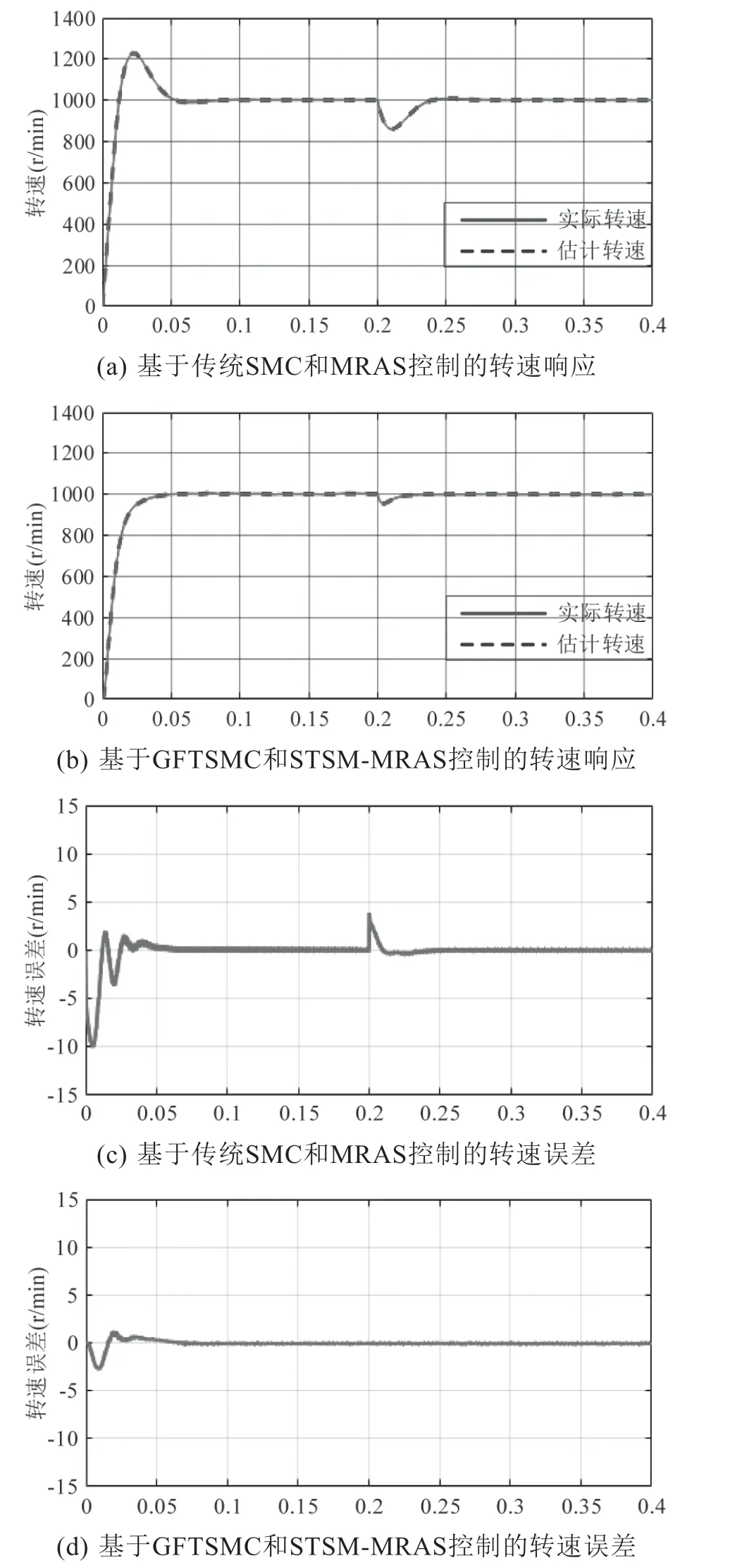
图4 负载扰动时两种控制策略的实际转速和估计转速的仿真对比图
从图4 的仿真结果来看,在前0.2 s 时,基于传统SMC 和MRAS 观测器的转速估计策略的转速波动较大,最大转速误差为10 r/min,达到稳定运行状态的时间为0.07 s,而基于本文所提转速估计策略的转速波动较小,最大转速误差为3 r/min,达到稳定运行状态的时间为0.055 s。当0.2 s 加入10 N·m 负载时,基于传统SMC 和MRAS 的转速估计策略的最大转速误差为4 r/min,达到稳定运行状态的时间为0.045 s,而基于本文所提转速估计策略的转速误差小于4 r/min,达到稳定运行状态的时间为0.025 s。
从上述两组仿真结果来看,相比于基于传统SMC 和MRAS 观测器的转速估计策略,本文所提基于GFTSMC 和STSM-MRAS 的转速估计策略能快速准确地收敛到实际值,转速误差更小,具有更好的动静态性能和抗干扰性。
为验证STSM-MRAS 观测器的估算转子位置性能。设定电机初始转速为1 000 r/min,在0.2 s 时加入10 N·m 的负载,仿真时间0.4 s。两种估计策略的转子位置估计结果如图5(a)和(b)所示,仿真图选取的时间0.15 s ~0.25 s 内的转子位置。两种估计策略的转子位置误差如图5(c)和(d)所示,选取的时间为0 s ~0.4 s。

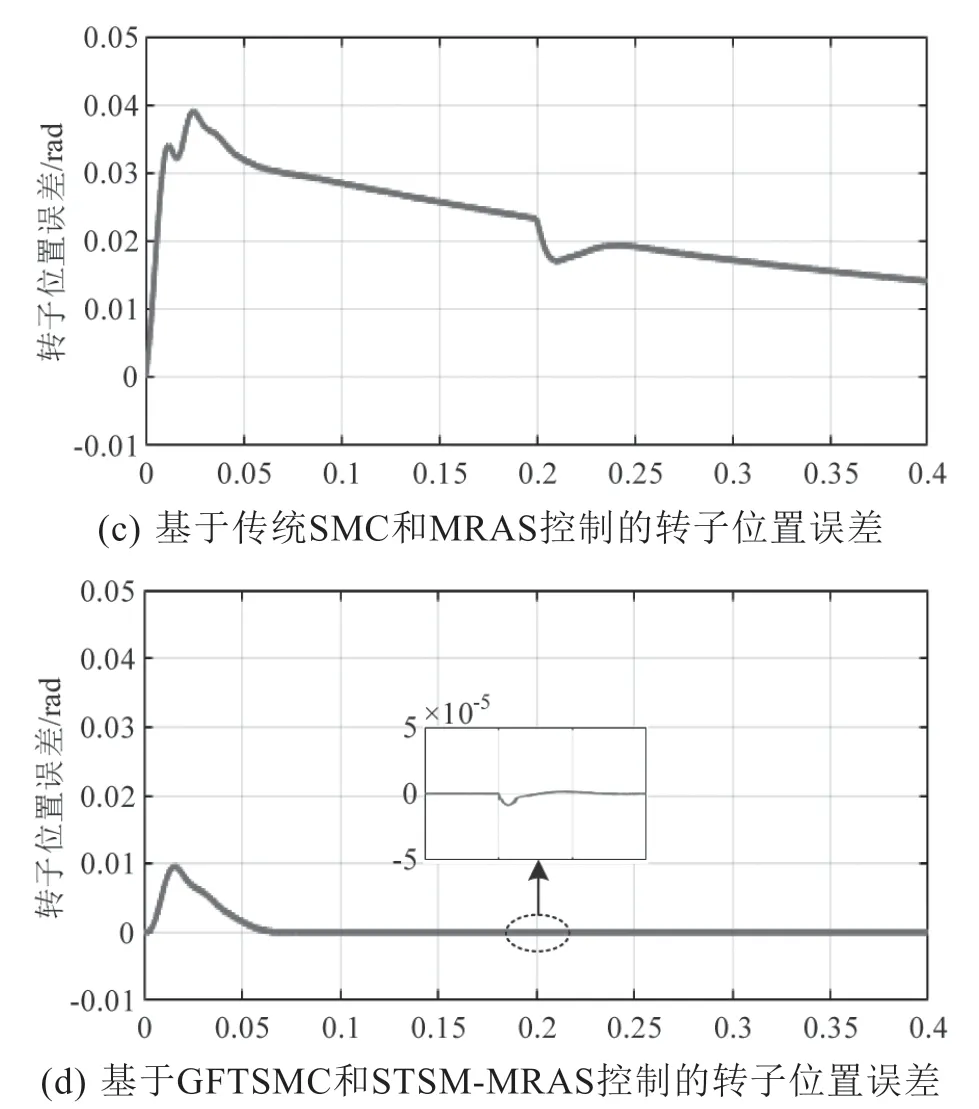
图5 负载扰动时两种控制策略下的转子位置估计情况
从图5 中可见,基于传统SMC 和MRAS的转速估计策略的最大转子位置误差为0.04 rad,而本文所提转速估计策略的最大转子位置误差为0.01 rad,收敛到零的时间为0.07 s。当0.2 s 时加入负载扰动时,本文所提转速估计策略仍能准确跟踪转子位置,转子位置误差较小。
5 结语
本文提出基于GFTSMC 控制器和超螺旋滑模MRAS 观测器的SPMSM 转速估计策略。控制器结合线性滑动模态和快速滑动模态构建新型滑模面,提高了滑模收敛速度,使状态误差能够在有限时间内收敛到零,有效地缓解了传统SMC 的相位延迟以及抖振问题。STSMMRAS 观测器引入了超螺旋滑模算法,削弱了滑模固有的抖振问题,提高了观测器的动态性能和鲁棒性,在负载扰动或转速变化的影响下,相比于基于传统SMC 和MRAS 观测器的转速估计策略,本文所提基于GFTSMC 和STSMMRAS 观测器的转速估计策略能够快速准确地估算电机的转速和转子位置,收敛速度快,估算精度高。通过对比仿真实验,验证了本文所提转速估计策略的可行性和有效性。

