基于数据可视化的电力数据融合及优化研究

徐国锋,钟晓红

(国网杭州市萧山区供电公司,浙江 杭州 311201)

随着计算机数据储存能力的提升,电力数据的储存量也快速增加。数据分类和整理的可视化预处理工作变得至关重要,给电力数据的可视化分析带来了挑战[1]。

可视化技术有着强大的数据计算能力和数据处理能力,方便人们从海量的数据中提取有价值的信息[2]。刘冬兰等[3]采用深度受限玻尔兹曼机将不同格式的异构数据映射到统一的嵌入式向量空间,实现了异构数据的融合。吴文宣等[4]提出一种多系统融合的移动电力巡检系统,实现关联系统之间的实时数据交互。胡健雄等[5]针对电力系统 4 种典型数据-物理融合模型分析了其相对应的应用场景,对比分析了并联模式与单一物理模型和单一数据模型的泛化误差。JI等[6]开发了基于数据融合的输电塔监测系统,并通过测试运行,验证了该系统能够安全稳定运行,能够获得准确可靠的测量数据,从而实现了塔架倾斜在线监测的功能。当前,关于基于智能数据可视化的数据融合研究较少。智能数据在最后的场景展示前,需要先对数据进行预处理,对数据进行分类融合,再进行筛选,为可视化工作减轻压力。神经网络具有函数逼近能力,具有一定的数据处理优势,例如具有较好的容错率和强大高效的数据分析功能,且数据处理效率较高,还具有自主学习能力[7]。充分利用神经网络的功能特征和结构特征,对数据进行融合,通过不断修正神经网络权值,可达到网络性能和软件服务的最佳优化程度[8]。

为提高电力数据融合性能,增强系统软件服务功能,在原有数据融合基础上,引入BP(back propagation)神经网络技术,形成基于BP神经网络的电力数据可视化融合软件系统,以某风电场电力数据为研究对象,对基于BP神经网络的电力数据可视化融合软件系统进行性能测试和分析。

1 理论概述与方法研究

1.1 数据可视化理论

可视化是利用计算机感知能力对数据进行可视化表达。利用计算机的图形分析功能,将抽象化的数据转换为详细、清晰的图形,使数据意义更直观[9]。数据可视化技术使用图形描述复杂数据信息,将数字数据转换成视觉模式,筛选和去除多余数据,最终以视图方式呈现[10]。通过将数据信息转换为计算机可处理的格式,并以视觉方式展示,以便挖掘数据背后的深层含义。

1.2 电力数据融合

电力数据融合技术是将多个电源和无组织的电网信息结合起来,准确、全面地感知电网场景的一种技术[11]。数据融合的理论最初是起源于多种传感器的综合应用。参与融合的数据由于来源多样化和数据格式多样化,因而具有多源异构性特点[12]。电力融合数据也具有自己独特的优点,比如容错性、全面性、准确性、有效利用性以及低成本性[13]。电力数据融合包括数据级、特征级和决策级3个级别[14]:数据级融合是对最初数据的融合,保留原始信息,减少数据损失,精度较高;特征级融合可以处理异构数据源,通过特征提取和关联分析,融合数据量减小,得到重要的特征向量;决策级数据融合是最高层次的融合,通过识别、特征提取和关联,合并判决结论,计算量最小。

1.3 关键技术

1.3.1 神经网络模式识别

模式识别是利用理论和方法,采用技术实现模式的解决与分类。人工神经网络模式识别具有智能性,在数据处理方面比其他算法更强大,具有较强的计算和自适应学习能力,能提取和分类识别特征[15]。模式识别包括数据获取、预处理、特征提取、数据训练和学习判定等部分。数据获取包括未经识别的训练样本或未知对象,分类决策在识别过程中起重要作用,对数据进行分类决策后得出结果,数据训练通过神经网络学习后输出权值。

1.3.2 神经网络模型

神经网络模型当前研究的热点包括不准确融合决策、统计的融合决策等。BP神经网络是比较常用的反向传播网络模型,分为输入层、隐含层和输出层[16]。在BP网络拓扑结构中,设输入层X=(x1,x2,…,xN),输出层Y=(Y1,Y2,…,YM),以Sigmoid函数作为隐含层的激活函数[17]:

(1)

式中:x为输入的数据;e为自然常数。

神经元的输入值X为:

(2)

式中:H为隐藏层层数;W为权值;i为神经元;j为神经网络的层数;n为信息量。

神经元的输出值Y为:

(3)

式中:f为激活函数。

在误差逆向回传时,Yj为预期输出,j∈[1,N],则误差e为:

(4)

BP网络的均方误差E为:

(5)

式中:R为层与层之间的距离;Yq为输出需要计算的层数。

由式(5)可得权值调整式:

(6)

式中:η为学习率;t为当前层的输出。

当输出值与期望值不相符时,可根据式(4)计算误差。对网络的误差值在网络各层之间进行反向传递,当误差梯度发生改变时,各层权值也随之发生改变。

1.4 基于BP神经网络的电力数据可视化融合软件系统架构

数据融合体系结构包括数据层、数据融合层、数据选择层和可视化层。数据层汇集了多种类型的数据,包括半结构化、非结构化和结构化数据,融合多源异质数据变得更加困难。数据融合层使用BP神经网络模型对数据进行初步分类,并挖掘隐藏的数据特征[18]。数据选择层进一步处理融合后的数据,筛选需要展示的部分,并通过减少数据量降低可视化的工作量。最后是可视化层,在这一层实现不同种类和形式数据的融合展示,分析数据之间的内在联系,并对系统性能进行测试和验证。

1.5 实验方法

1.5.1 实验测试及误差标准分析

为验证所提方法,对风电机组多状态电力系统调度中的应用性能进行实验测试。实验针对风电场发电的功率预测采用均方根误差RMSE和平均绝对百分误差MAPE作为最终结果的分析标准:

(7)

(8)

式中:M为输出层神经元的数量;N为输入层神经元的数量;Xpi为预测值;XMi为实际值。RMSE值和MAPE值越小,预测越精确,预测效果越好。

1.5.2 测试运行环境

测试数据来自2020年7月某风力发电场的历史监测数据,数据量总大小为100GB,利用BP神经网络算法对电力系统风电场功率数据进行迭代训练,将设计算法与其他方法进行对比分析,对风电场功率进行预测。系统运行环境包括系统硬件配置和软件配置,具体如表1所示。

表1 系统配置表

2 功能测试与结果分析

2.1 BP神经网络算法精度分析

BP神经网络算法下的权值元素迭代法和矩阵迭代法训练的精确度对比如图1～图2所示。

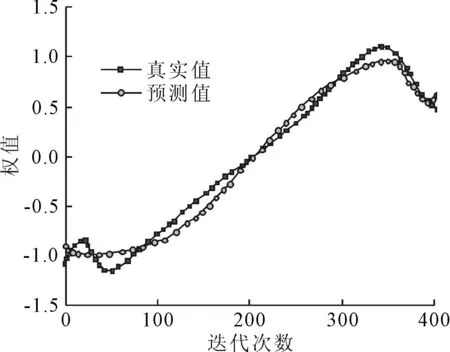
图1 权值元素迭代法训练下的权值准确度

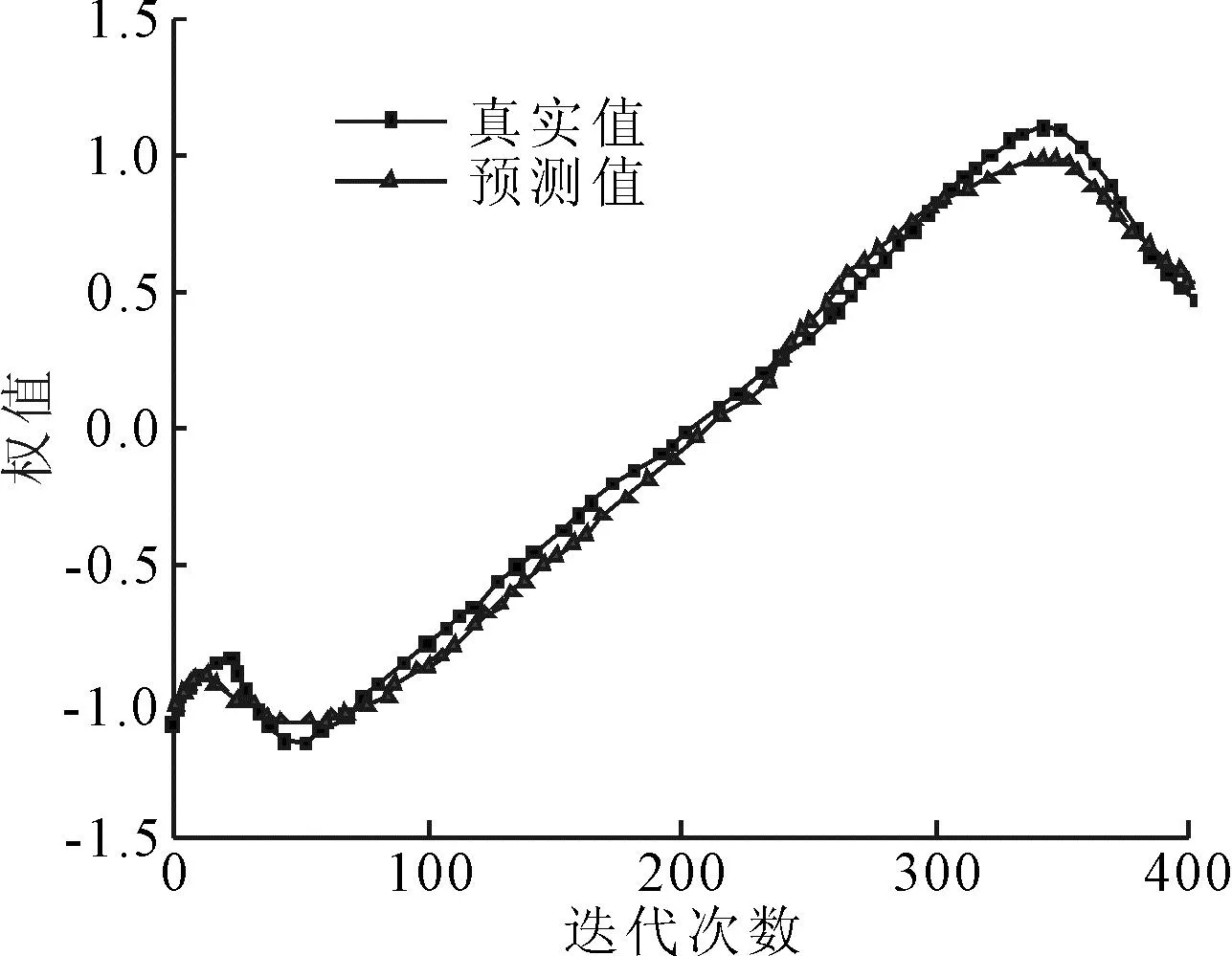
图2 矩阵迭代法训练下的权值准确度

由图1可知,BP神经网络算法下的权值元素迭代法得出的数据预测值与真实值对比,经过400次的迭代训练,权值大小趋于接近状态。在前期的迭代训练中,权值精度存在一定的差距,尤其是当迭代次数在50和350时,真实值与预测值偏差更为明显。由图2可知,矩阵迭代法得出的数据预测值更接近真实值,偏差较小,能够进一步确定权值。经过400次迭代后预测值接近真实值。BP神经网络算法下基于矩阵迭代法训练神经网络达到了更好的收敛效果,更能逼近真实值,其性能优于基于元素迭代法训练的神经网络。

2.2 不同算法下的风电场功率预测准确度分析

将设计算法与贝叶斯推理法、聚类分析法进行对比,将不同算法下的预测曲线与实际功率曲线作比较,结果如图3所示。

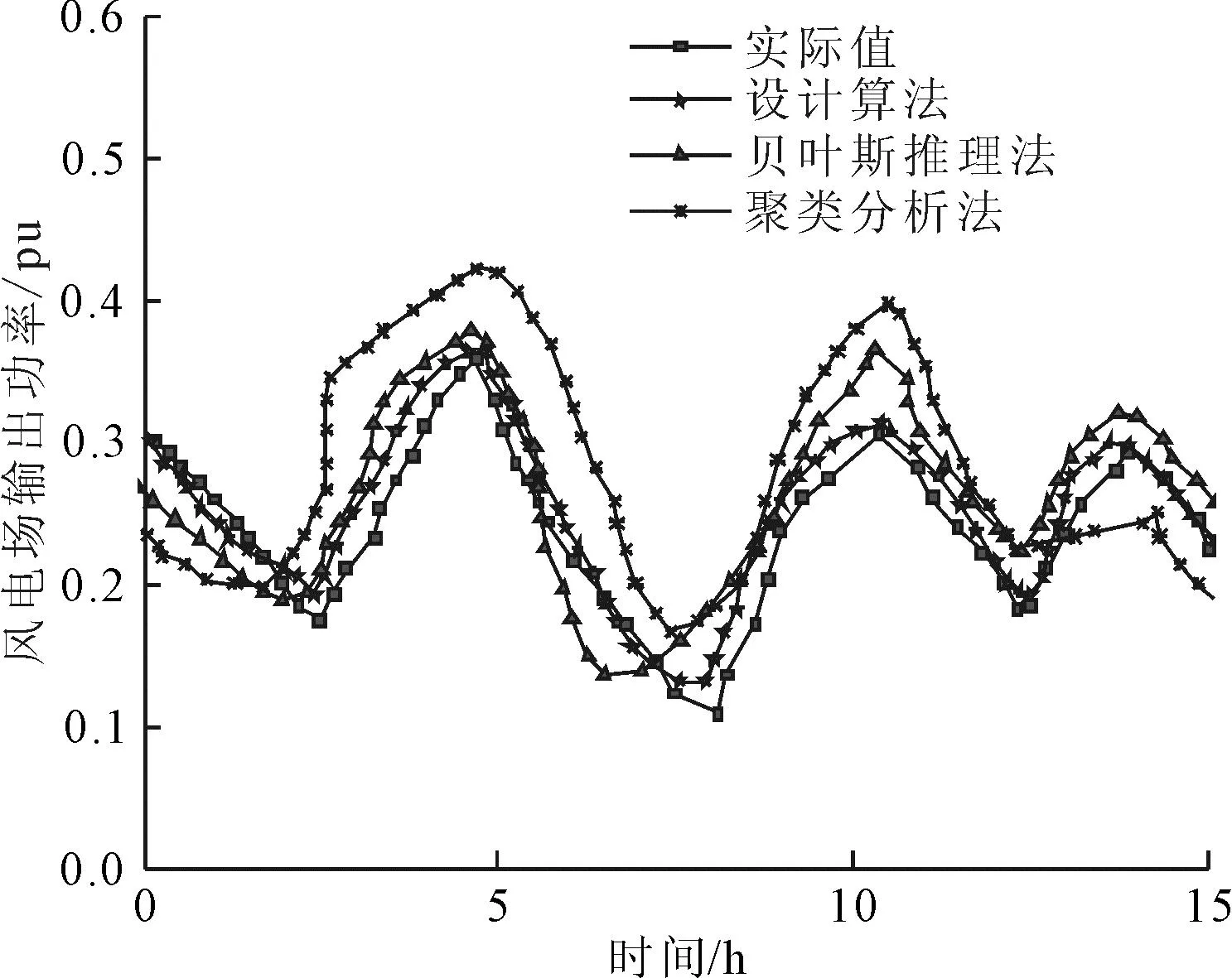
图3 不同算法下的功率预测对比

由图3可知,设计算法的输出功率预测最接近实际值,其次是贝叶斯推理法,最后是聚类分析法。设计算法输出功率相比其他算法更接近于真实值。由此可知,设计算法对风电场功率预测具有较高的准确度。

2.3 不同算法下的误差分析

对数据结果进行均方根误差(RMSE)和平均绝对百分误差(MAPE)分析,对比不同算法下的误差结果,结果如图4～图5所示。

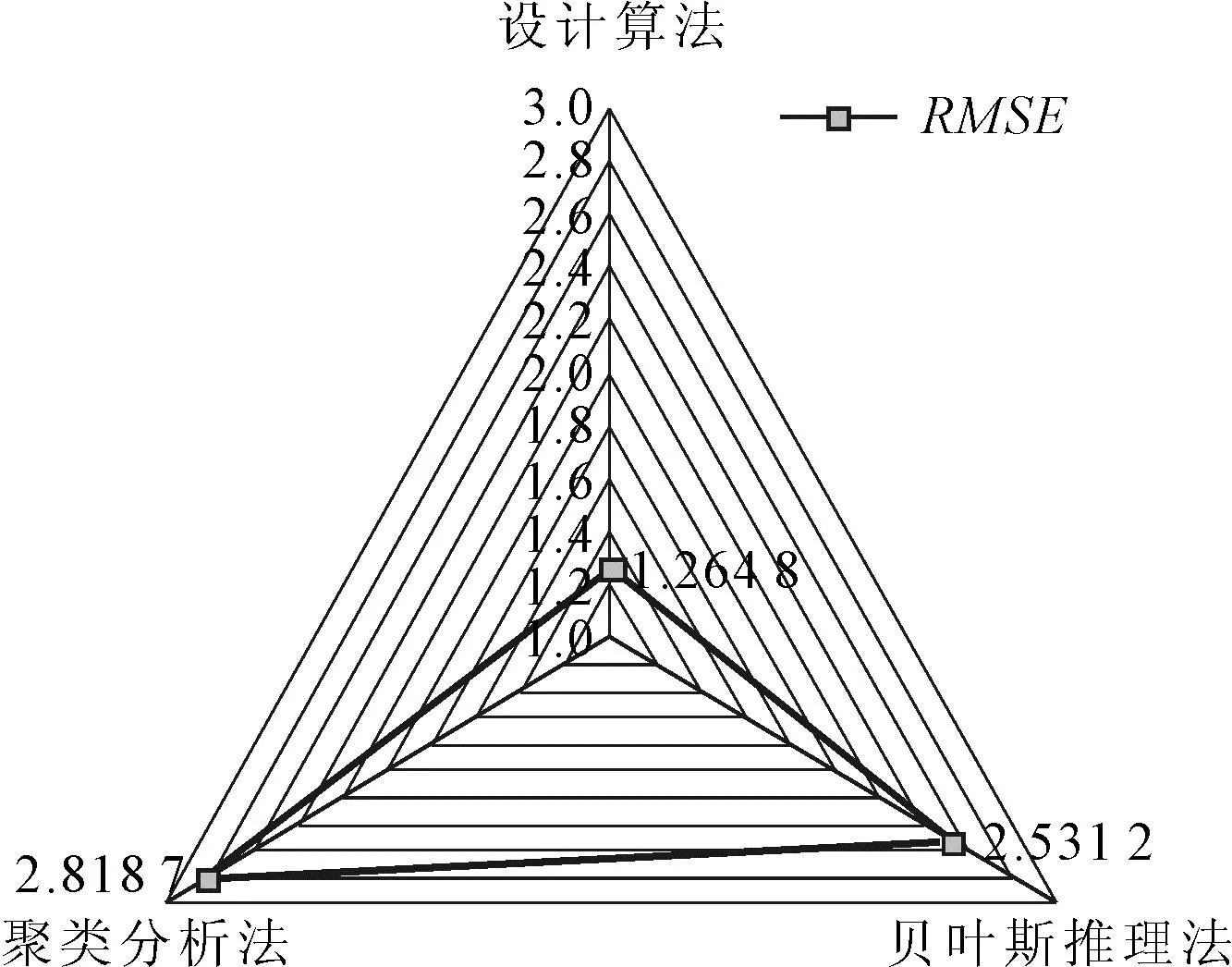
图4 不同融合算法的RMSE对比

图5 不同融合算法的MAPE对比

由图4可知,设计算法、贝叶斯推理法、聚类分析法的均方根误差分别为1.264 8、2.531 2和2.818 7,设计算法的均方根误差最小。由图5可知,设计算法的平均绝对百分误差值波动范围较小,而贝叶斯推理法误差值波动较大,聚类分析法误差值波动最大。总体上设计算法的误差值相对于其他算法均有所下降,误差更小。

2.4 不同算法下的处理时间分析

利用不同的算法计算数据量,分析不同算法对不同数据量的处理时间,结果如图6所示。

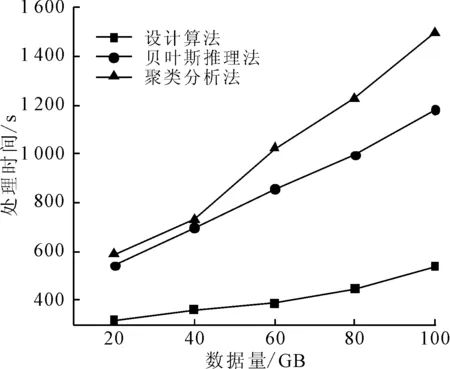
图6 不同算法下的数据处理时间比较

由图6可知,当数据量相同时,贝叶斯推理法、聚类分析法的数据处理时间均大于设计算法的数据处理时间,随着数据量不断增加,数据处理时间逐渐加大,设计算法的处理时间幅度变化较小,而贝叶斯推理法、聚类分析法的数据处理时间增长幅度较大。尤其是当数据量超过40 GB以后,时间差距逐渐增大。整体上设计算法数据处理时间增加趋势较为减缓,当数据量达到100 GB时设计算法处理时间不到600 s,而其他算法处理时间均超过1 100 s。

3 结论

人工神经网络具有自学习和自组织能力,可以充分利用其功能和结构特征对数据进行融合,提高数据可视化能力。研究在原有数据融合基础上,引入BP神经网络技术,形成基于BP神经网络的电力数据可视化融合系统。通过实验测试,分析不同训练方法下的BP神经网络算法精度,风电场功率预测准确度,不同算法下的均方根误差和平均绝对百分误差,最后对数据处理时间进行对比分析。结果表明:经矩阵迭代法训练的神经网络在风电场功率预测方面表现出更好的收敛性。经过400次迭代训练后,BP神经网络算法的预测值更接近真实值,数据训练效果更优。与贝叶斯推理法和聚类分析法相比,设计算法具有更高的准确度。该算法在均方根误差和平均绝对百分误差上的误差范围更小,且达到最小误差值。此外,设计算法能够高效处理大数据,在100 GB数据量下的处理时间不到600 s,远快于其他算法超过1 100 s的处理时间。在智能数据可视化和电力数据融合方面,设计算法表现出较好的性能和效率。未来还将扩大数据量,为处理更大规模的数据提供实验依据,并研究非结构化数据的融合和处理策略。