基于随机平均法的框架-摇摆墙结构随机激励响应分析

王冠达,张远进,许伊键

(1.武汉理工大学 中国应急管理研究中心,湖北 武汉430070;2.武汉理工大学 安全科学与应急管理学院,湖北 武汉 430070;3.合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

地震会给人们带来巨大的灾难,阻碍城市发展。人们通过不断发展新理论、改善建筑结构,以将地震带来的损失降到最低[1]。在当今建筑结构中,应用较为广泛的是钢筋混凝土框架结构,但此类结构在地震中容易产生不可修复的损伤[2]。结构在地震作用下会产生一定的变形,同时经历能量耗散过程,产生不同程度的损伤,当损伤发展到一定程度后,结构将失效或倒塌[3]。框架结构的损伤破坏往往发生于少数楼层变形而形成的层屈服机制[4]。

国内外学者提出“可恢复功能”的抗震结构体系,为了减少地震中不可修复的损伤、提高结构的抗震性能,摇摆墙被引入到框架结构中,形成了框架-摇摆墙结构[5]。该结构由框架与摇摆墙两部分组成,两者之间通过刚性链杆连接,以摇摆墙结构缓解框架的受力情况,减轻或者避免产生层屈服机制。AJRAB等[6]对框架-摇摆墙结构进行非线性时程分析,发现在地震作用下,框架-摇摆墙结构的层间位移分布比传统框剪结构更均匀。HU等[7]使用时程分析法,将纯框架结构与附加自复位墙的框架结构进行动力响应分析比较,发现附加自复位墙后,结构的动力响应明显减小,基本无残余位移产生。杨树标等[8]设计了一种新型框架-摇摆填充墙结构,并进行静力非线性分析,结果表明摇摆填充墙能够改善建筑结构层间位移分布,使结构层间位移趋于均匀,将结构破坏机制改变为整体破坏机制,明显改善了框架结构的延展性。田会文等[9]针对自复位墙在矩形脉冲作用下的动力响应进行分析,发现自复位墙倾覆谱附加安全区域SN的位置和面积与墙体高宽比、预应力筋初张力和刚度均有关。

随机平均法是分析非线性随机系统响应的有效方法之一。20世纪60年代,STRATONOVICH[10]首次提出随机平均法,迄今为止,许多学者在随机激励下的非线性系统响应分析中运用随机平均法。SANTOS等[11]利用基于Hilbert变换的随机平均法,给出了一种半解析方法,用于确定随机激励非线性振子的生存概率和首次穿越时间概率密度函数。SPANOS等[12]使用随机平均法导出了振荡器非平稳边缘、过渡和联合响应振幅PDF的近似封闭形式表达式,并最终导出了随时间变化的振荡器生存概率。KOUGIOUMTZOGLOU等[13]依靠统计线性化和随机平均的组合产生具有时变刚度和阻尼元件的等效线性系统(ELS)。VANVINCKENROYE等[14]依靠响应能量包络的马尔可夫近似和随机平均处理,得到一个控制振荡器可靠性函数随时间演变的后向Kolmogorov方程。CHAI等[15]基于能量包络随机平均法和路径积分法研究了随机横浪中非线性横摇运动的随机响应,使用随机平均法对原系统进行降维,降低了计算随机响应的难度。解娜娜等[16]研究了含有惯性非线性的梁振动方程在高斯白噪声激励下的随机平均法。

笔者针对单自由度框架-摇摆墙结构在随机地震激励下,摇摆墙体发生偏转抬升,并进行往复摇摆运动这一现象,建立动力响应方程并进行分析,将系统的运动方程进行一定的简化后,运用随机平均法求解系统的等价刚度与阻尼。

1 框架-摇摆墙动力学方程

框架与摇摆墙之间采用刚性链杆L进行连接,位于框架右顶点与摇摆墙左顶点之间。设结构转动时,链杆L与水平线夹角为Φ,矩形摇摆墙高度为2h,宽度为2b,框架质点与地面的相对位移为Us,摇摆墙左顶点与地面相对位移为Ut。假设忽略主体框架与摇摆墙体的竖向变形,摇摆墙为刚体,且质量集中在墙形心。摇摆墙角O点与O′点各设置有一个金属阻尼器。当单自由度框架-摇摆墙向正方向运动时,即墙体转动角θ>0,当结构向负方向运动时,即θ<0,如图1所示。

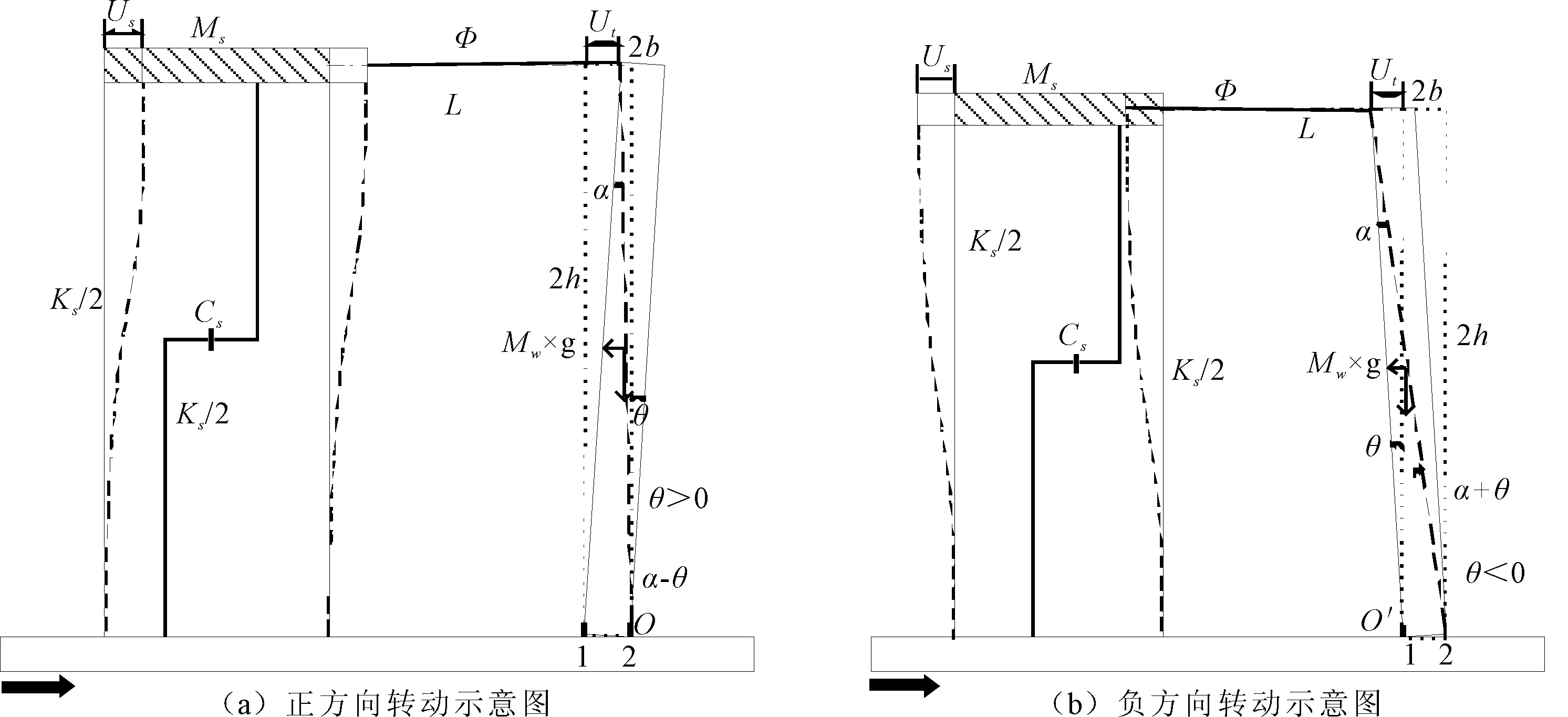
图1 结构转动示意图

当θ>0时,根据达朗贝尔原理,对O点列力矩平衡方程:

(1)

Ug表示地面位移,Us表示框架质点与地面的相对位移,U表示框架质点的绝对位移,则U(t)=Ug(t)+Us(t)。当单自由度框架-摇摆墙运动时,框架质点与地面的相对位移Us为:

Us=Ut=±2R[sinα-sin(α∓θ)]

(2)

当θ>0时,±处取正号,∓处取负号;当θ<0时,±处取负号,∓处取正号。

在随机地震激励作用下,框架的动力学方程可表示为:

(3)

将式(2)代入式(1)可得:

(4)

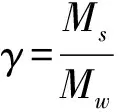
当θ<0时,根据达朗贝尔原理,对O′点列力矩平衡方程:

(5)

式中:f2为右侧金属阻尼器的恢复力。将式(2)代入式(5)可得:

(6)

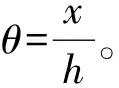
(7)

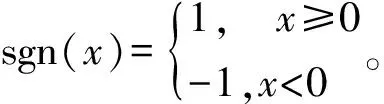
2 随机平均法

根据参考文献[17],由式(7)可知:

(8)

(9)

(10)

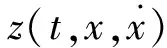
(11)

(12)

(13)

(14)

(15)

式中:A为响应位移的时间相关幅度;φ为相位,是与时间t相关的函数。A和φ都具有随时间缓慢变化的特性,因此可在一个周期内认为其近似恒定。

将式(7)代入式(12)～式(15)可知:

(16)

(17)

对式(12)、式(13)的右侧求期望可以得到近似等效的时间相关阻尼因子和频率:

(18)

(19)

式中:c(t)为非平稳随机响应的方差。

此时,在模拟地震随机激励下的单自由度框架-摇摆墙结构的动力响应方程可以表示为:

(20)

式中:p(A,t)表示响应过程x的幅值A的概率密度函数,如式(21)所示;c(t)为随机响应过程x与时间相关的方差,可由微分方程描述,如式(22)所示。

(21)

(22)

根据式(22)求得随机激励下单自由度框架-摇摆墙位移响应的方差,将其与MCS的结果进行对比,可以验证随机平均法模拟结果的可靠性。

3 数值算例

3.1 模型参数

采用单自由度框架-摇摆墙结构模型,摇摆墙尺寸为4 m×1 m×0.1 m,γ=2 000,Ks=7.2×107N/g,Ms=2×106N/g,ξs=0.05,Mw=1 000 N/g,fd=7×104N。

3.2 随机激励模型

在模拟地震随机激励时采取非平稳地震动模型,地震动加速度可以表示为:

(23)

式中:a0(t)为平稳白噪声过程,其功率谱密度函数为S0;ψ(t)为Amin 和Ang型调制函数[18],其表达式如式(24)所示。

(24)

调制函数各参数按照文献[19]中取值,即A0=0.412 3,a=0.85,t1=1.47 s,t2=6.47 s。将式(23)代入式(10)可得:

(25)

随机激励的功率谱密度函数为:

(26)

3.3 数值分析

采用MCS法(样本数为4 000条)验证随机平均法计算结果的HJ可靠性,对比分析不同激励强度S0(0.8 m2/s3、0.9 m2/s3、1.7 m2/s3)时的结构响应,可以得到所提模型在非平稳随机激励下位移响应的方差,结果如图2所示。由图2可知,单自由度框架-摇摆墙模型在调制白噪声激励下,不同激励强度仅对结构位移响应的方差大小产生影响,随机平均法与MCS法的结果较为接近。

图2 随机平均法与MCS的位移方差

为验证随机平均法求得位移响应方差分布的准确性,绘制其概率密度函数图像,根据Amin 和 Ang 型分段调制函数,在其上升、平稳、衰减阶段分别任意取一个时间点,t=1 s,t=2 s,t=7.5 s。为研究在非平稳随机激励的作用下激励强度对结构响应的影响,对比分析不同激励强度S0(0.8 m2/s3、0.9 m2/s3、1.7 m2/s3)时结构响应位移方差的概率密度函数,如图3所示。由图3可知,单自由度框架-摇摆墙模型在不同强度的调制白噪声激励下,随机平均法求解得的位移响应方差的概率密度函数与MCS模拟结果的峰值与分布均比较相似,拟合准确性较高。

图3 不同激励强度结构相应位移方差的概率密度函数

4 结论

(1)为探讨单自由度框架-摇摆墙结构模型在模拟地震的随机激励下的动力响应,建立该结构向正、负两个方向转动的运动方程,将与角度相关的运动方程转化为与位移相关的运动方程,具有较高的分析精度和合理性。

(2)采用随机平均法求出单自由度框架-摇摆墙结构的等效线性运动方程,其位移响应的方差与MCS法的结果接近,验证了随机平均法在应用于该结构地震响应分析的适用性。

(3)以所求得的等效线性运动方程进行结构响应的数值模拟,在不同激励强度下方差的概率密度函数与MCS求得方差的概率密度函数拟合度较高,由此可知本文方法准确性较高,可靠性较强,进一步验证了方法的合理性和可靠性。