网络舆情影响下考虑心理参照点变化的多阶段群决策方法

王治莹,王韦棋

(安徽工业大学 管理科学与工程学院,安徽 马鞍山 243032)

据中国互联网络中心公布的报告显示,截至2022年,中国网民规模达到10.67亿,互联网普及率高达75.6%。同时,近年来频繁爆发的突发公共事件借助网络媒体迅速传播,常常引发舆情危机,其破坏力在网络舆情的推动下被无限放大,增加了突发公共事件的处理难度。一旦网络舆情中的某些虚假信息得不到有效管控,极有可能衍生出次生事件,进而对居民生活和社会治安造成巨大的负面影响。因此,在应对突发公共事件时应充分考虑网络舆情的影响,并通过适当引导网络舆情走向来减少突发公共事件对社会的危害。

目前,网络舆情影响下的多阶段群决策问题研究主要集中在网络舆情管控和突发公共事件应急决策两个方面。首先,针对网络舆情管控问题,国内外学者从网络舆情传播机理分析和网络舆情演化态势预测开展了研究。在网络舆情传播机理分析方面,聂琦等[1]认为网络舆情的传播机理与传染病的扩散机理类似;WANG等[2]构建了网络舆情时空演化分析模型和影响因素分析模型,分析了疫情严重程度、网民数量、媒体报道数量和区域属性等多种因素共同影响下的网络舆情时空演变过程;WANG等[3]采用计量经济模型对舆情信息进行了多维因素分析;ZHANG等[4]对传染病模型(SIRS)进行改进,将舆情网络节点分成高影响层和低影响层,引入层内和层间信息传输机制,构建了分层SIRS信息传输模型;庞庆华等[5]探索了意见领袖影响下微博负面舆情的演化规律,并构建了政府、媒体和网民的三方演化博弈模型。关于网络舆情演化态势预测的研究,主要采用logistic模型[6]、神经网络[7]、灰色模型[8]、系统动力学[9]、马尔科夫模型[10]等方法。鲜有研究采用隐马尔可夫模型对网络舆情态势进行预测,隐马尔科夫模型能够处理具有时序关系的数据和进行序列预测,且可通过观测数据反映实际状态,因此采用隐马尔科夫预测舆情态势与实际情况更符合。其次,针对突发公共事件应急决策的研究,胡彦等[11]引入三支决策和前景理论构建模糊多属性应急决策模型;樊自甫等[12]提出基于区间值模糊熵构建应急群决策模型;童玉珍等[13]提出基于犹豫模糊集的突发公共事件网络舆情应急群决策方法。然而以上研究均未考虑突发公共事件演化过程的多阶段性。王治莹等[14]提出一种考虑决策者情绪对心理参照点影响的多阶段应急决策方法;吴凤平等[15]提出一种多阶段多目标的动态应急决策方法,并使用等差数列对多阶段时间序列权重进行赋值。但上述研究未考虑网络舆情对决策者心理参照点和突发公共事件应急决策的影响。

综上所述,以往研究未考虑网络舆情对决策者心理参照点变化和突发公共事件演化态势的影响,而网络舆情演化态势预测的研究中也鲜有考虑应急方案对舆情演化的影响。此外,如何建立网络舆情影响下的决策者心理参照点更新方法成为突发公共事件多阶段群体决策亟待解决的问题。基于此,笔者提出一种网络舆情影响下考虑决策者心理参照点变化的突发公共事件多阶段群体决策方法。主要创新点:一是基于隐马尔科夫模型预测了考虑应急方案影响的网络舆情演化过程;二是基于事态演化趋势更新决策者心理参照点,同时考虑不同决策者风险偏好异质性,引入决策者损益敏感度因子。

1 理论基础

1.1 隐马尔科夫模型

隐马尔科夫模型[16](HMM)是一种有关时序的概率模型,包含状态集和与状态对应的观测序列。状态间的转移由状态转移概率矩阵表示。观测序列不是状态本身,故根据观测序列得到隐状态的过程称为隐马尔科夫过程。HMM由初始概率分布、状态转移概率分布和观测概率分布决定。

假设所有状态序列的集合为X=(x1,x2,…,xn);所有观测序列的集合为Y=(y1,y2,…,ym);长度为T的状态序列为W={w1,w2,…,wT};相对应的观测序列为Z={z1,z2,…,zT};则初始状态概率矩阵为σ=[σi]1×n,σi=P(w1=xi),1≤i≤n,表示在t=1时状态为xi的概率;状态转移概率矩阵为E=[eij]n×m,eij=P{wt+1=xj|wt=xi},1≤i,j≤n,eij为从t时刻状态xi转移到t+1时刻xj的概率;观测值概率矩阵为F=[fj(k)]n×m,fj(k)=P(zt=yk|wt=xj),1≤j≤n,1≤k≤m,表示t时刻在状态xj的条件下观测值为yk的概率。综上,σ和E决定状态序列,F决定观测序列,三者共同决定模型参数。因此,将HMM模型参数η表示为η=(σ,E,F)。

1.2 累积前景理论

累积前景理论[17](cumulated prospected theory,CPT)是一种关于决策者行为的理论,传统的期望效用理论假设决策者完全理性,这与事实不符,CPT的提出弥补了期望效用理论关于理性假设的不足,在决策时会综合考虑人的风险偏好和心理感知价值等因素。价值函数表示为:

(1)

式中:Δxi为决策结果相对于参照点的损益,Δxi≥0代表决策者收益,Δxi<0代表决策者损失;α和β分别为风险厌恶系数和风险偏好系数;λ为损失规避系数。通常取α=0.89,β=0.92,λ=2.25[18]。决策者对收益和损失的决策权重函数为:

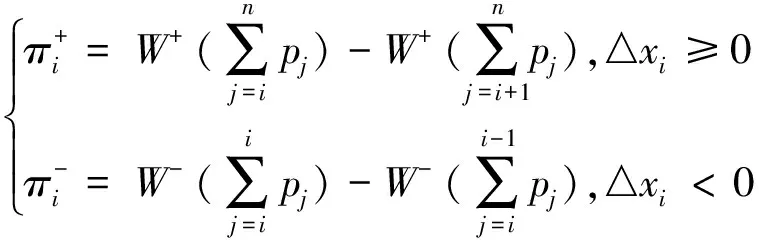
(2)

(3)

式中:W+(·)和W-(·)均为非线性函数;χ和δ分别为决策者对收益和损失的态度,通常取χ=0.61,δ=0.69。

2 问题描述

突发公共事件的演化过程具有多阶段、易变化、不确定等特点,决策者在制定应急决策方案时往往不能一蹴而就,而是依据事态等级动态调整应急方案。同时,由突发公共事件引发的网络舆情也会对突发公共事件的演化过程造成影响,如若不加控制,极易引发舆情危机。反之,突发公共事件的演化及处理过程也会对网络舆情的演化过程造成影响。因此,网络舆情与突发公共事件之间的耦合演化关系增加了网络舆情态势预测及突发公共事件应急决策的难度。

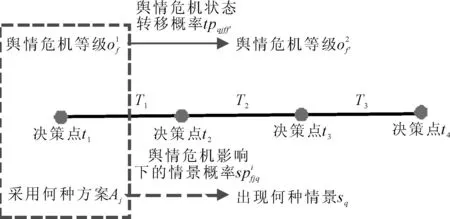
图1 网络舆情影响下的突发公共事件多阶段决策过程

基于突发公共事件演化的多阶段性以及网络舆情与突发公共事件演化的耦合性,设计一套科学的决策方法,通过考虑决策者人员伤亡、财产损失和舆情态势的心理参照点受突发公共事件演化态势影响动态变化,建立决策者心理参照点更新机制,并综合考虑人员伤亡、财产损失、舆情态势及应急决策方案的投入成本、准备时间、可行性、风险指数、舆情传播广度等多种指标,通过累积前景理论计算得到备选应急方案的优劣次序,辅助应急管理部门对突发公共事件进行处理。网络舆情影响下的多阶段群决策方法如图2所示。

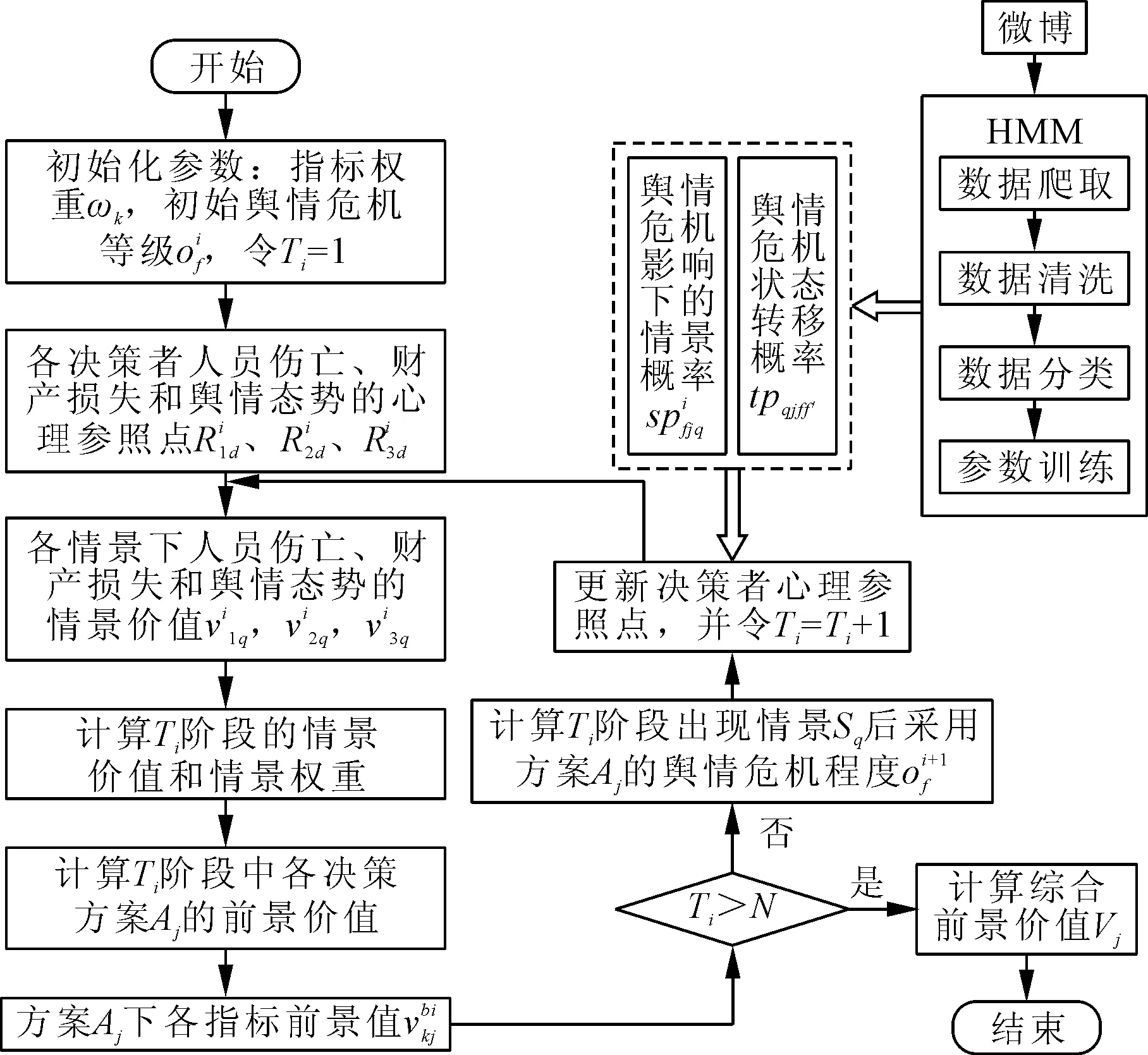
图2 网络舆情影响下的多阶段群决策方法

3 基于HMM的舆情态势预测

突发公共事件的网络舆情危机等级无法直接通过数据显示,但与网民规模、网民活跃度、平台传播趋势、网民情感倾向等可观测数据紧密相关,故将这些指标作为观测序列,将舆情危机等级作为隐状态。

(1)HMM节点状态设定。充分考虑突发公共事件各种情景下网络舆情的定量和定性数据的特点,将各节点状态划分如下:①突发公共事件情景节点状态设定,决策点只能有一种情景发生,将决策点发生的情景的状态表示为T,其他情景状态表示为F;②备选方案节点的状态设定,根据突发事件的演化进程及决策者的研判,最终决策只能选一种方案,被选择的方案状态为T,其他方案为F。③网民规模状态划分,指在一段时间内网民浏览事件信息的次数和点赞量。浏览次数和点赞量越多,网民规模越大,舆情热度越高。因此,将网民规模的状态划分为高(H)、中(M)、低(S)。④网民活跃度状态划分,网民对相关话题发表评论的微博总数量,发表的评论数量越多,网民活跃度越高,对事件的关注度越高,舆情热度越高。将网民活跃度划分为高(H)、中(M)、低(S)。⑤平台传播趋势状态划分,指事件一段时间内在微博等网络平台上传播的效果,将平台传播趋势划分为高(H)、中(M)、低(S)。⑥网民情感倾向状态划分,分别为积极情感(P)、中性情感(M)和消极情感(N)。⑦舆情危机等级划分,分别为红色预警(Ⅰ级)、橙色预警(Ⅱ级)、黄色预警(Ⅲ级)和蓝色预警(Ⅳ级)。

(2)HMM参数学习。在使用HMM预测网络舆情演化态势时,首先需要获得HMM的三元要素η=(σ,E,F)。由于无明确状态序列,属于无监督学习过程,Baum-Welch算法是一种经典的无监督学习算法,故采用Baum-Welch算法训练HMM参数。假设已知数据只包含了m个长度为T维的观测序列{Z1,Z2,…,Zm},没有给出相应的状态序列,为学习HMM的参数η=(σ,E,F),将观测序列数据设为观测数据Z,状态序列数据设为不可观测的隐数据W,故HMM是一个带有隐变量的概率模型,如式(4)所示,参数学习过程参考文献[19],具体如式(5)～式(7)所示。

(4)

(5)

(6)

(7)

4 基于CPT的多阶段应急决策方法

4.1 基于熵权法的评价指标赋权

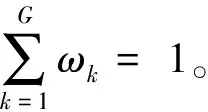
(8)

(9)

(10)

4.2 指标属性值规范化

决策者在做效用评价时,通常有精确值、区间值和自然语言等多种不同数据类型的指标。为了统一比较标准,需对原始数据进行规范化、标准化处理。考虑到实际决策信息往往具有模糊性、不确定性,因此将不同种数据类型转换成直觉模糊数的形式,其表达形式为A=(μA(x),vA(x)),μA(x)表示元素x的隶属度,vA(x)表示元素x的非隶属度,πA(x)=1-μA(x)-vA(x)表示x属于A的犹豫度。

(11)

(12)

(13)

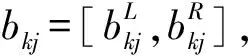
表1 语言变量转化表

(14)

4.3 基于事态演化趋势的心理参照点更新方法

4.4 计算情景价值

4.5 计算情景权重

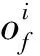
πfj(t)=

(15)

式中:πfj(h)=ω+(pfj(h))、πfj(n)=ω-(pfj(n)),f=1,2,…,L,j=1,2,…,M;ω+(·)、ω-(·)分别表示“收益”和“损失”的权重函数,ω+(p)=pγ/(pγ+(1-p)γ)1/γ,ω-(p)=pδ/(pδ+(1-p)δ)1/δ,γ=0.61,δ=0.69。

4.6 计算方案综合前景值

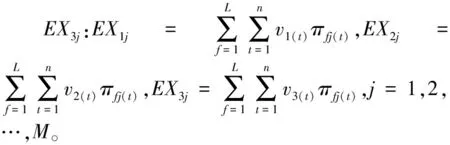
5 算例分析

某地爆发传染病,经过传染病学专家分析疫情将持续3个阶段,每个阶段都可能出现以下4种情景。S1:疫情得到全面控制,可能造成的人员伤亡数为5～10人,经济损失为50～100万元,舆情态势为[0.0,0.3];S2:疫情在少数地区失控,可能造成的人员伤亡数为10～15人,经济损失为100～200万元,舆情态势为[0.3,0.5];S3:疫情在多数地区失控,可能造成的人员伤亡数为20～30人,经济损失为200～500万元,舆情态势为[0.5,0.7];S4:疫情全面失控,可能造成的人员伤亡数为50～100人,经济损失为500～700万元,舆情态势为[0.7,1.0]。为应对该突发疫情事件,决策者制定4个应急方案。各应急决策备选方案的评价指标如表2所示。

表2 应急决策方案的评价指标

各决策者在决策时主要依据8个指标对流行性传染病进行应急响应:B1投入成本,B2准备时间,B3可行性,B4风险指数,B5舆情传播广度,B6人员伤亡,B7财产损失,B8舆情态势。4名决策者给出的不同指标的权重如表3所示。

表3 各决策者对各指标的权重

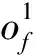
表4 舆情危机状态转移概率矩阵

6 结论

(1)针对突发公共事件演化过程受网络舆情态势影响可能导致决策结果不同的问题,提出了一种网络舆情影响下考虑决策者心理参照点变化的多阶段群决策方法。不仅考虑了突发公共事件的多阶段特征和多决策者对各指标评价不一致的情形,还考虑了网络舆情演化态势对决策者心理参照点的影响进而对应急决策结果产生影响,为多阶段群决策提供了新思路。

(2)采用HMM预测各情景和应急方案下网络舆情演化趋势,并得到各网络舆情态势下情景转移概率;同时,针对决策者不同阶段心理参照点转移,提出基于突发公共事件演化态势的决策者心理参照点更新机制,并考虑了不同决策者风险偏好异质性,引入损益敏感度改进决策者心理参照点更新机制。

(3)舆情信息从孕育、发展,到爆发,具有时滞性。因此,未来可考虑网络舆情信息的时滞性,使用具有时滞效应的灰色模型对网络舆情进行预测,可能会更加贴合网络舆情传播机理,得到更佳的决策结果。