安全多方计算应用的隐私度量方法

熊 维 王海洋 唐祎飞 刘 伟

1(神州融安数字科技(北京)有限公司 北京 100086) 2(北京国际大数据交易有限公司 北京 100020) 3(大数据协同安全技术国家工程研究中心 北京 100071)

传统的计算模型如单机状态的图灵机模型,其计算的输入、输出和运算程序都由一方独自占有.多方计算是指由多个参与者提供数据或计算资源并进行联合计算的情况,其相对于单方计算会引发诸如公平性、数据隐私、计算成本等问题.常见的概念例如安全多方计算、外包计算、分布式计算、多方提供数据的中心式计算等均属于多方计算的范畴.其中,安全多方计算(secure multi-party computation, MPC)的基本思想是Yao等人[1]于20世纪80年代提出的,它是指在无可信第三方的情况下,多个参与者可以安全地计算一个约定函数的系统.安全地计算指在函数计算过程中每个参与者不能获得其他参与者的输入和输出信息.

影响安全多方计算方案隐私信息泄露的因素众多,设计一个既安全又高效的安全多方计算的实现方案很具有挑战性,这促使人们寻求方案可用性和隐私性之间的平衡.目前,安全多方计算研究多集中在如何防止计算过程中隐私信息的泄露,也就是说如何防止1个参与者通过计算过程获得其他参与者输入或输出的信息.然而,1个参与者通过其合法的函数输入和输出推导出其他参与者输入信息或者输出信息的可能性却没有进行充分研究.

本文关注的是理想多方计算情况下目标函数本身对参与者输入提供的保护程度,只有能够衡量各个参与者在这种情况下隐私泄露的程度,才能真正评估各个参与者在实际进行安全多方计算应用过程中的隐私泄露情况.因此,隐私度量的研究对安全多方计算的应用和部署具有理论意义和实践价值.

基于Shannon[2]提出的信息熵理论,本文首先研究并提出理想多方计算模型下目标函数对各方数据隐私保护的度量方法,进而提出实际情况下的安全多方计算的隐私保护强度的概念,最后提出隐私保护成本的计算方法.本文主要贡献如下:1)针对理想多方计算模型,从攻击者的角度定义平均熵和特定熵的概念,提出计算信息收益的方法,从而描述在攻击者的视角下其他参与者特定的输入对攻击者输出分布的影响程度;2)通过计算目标函数的理想隐私损耗和实际安全多方计算应用中的实际隐私损耗,衡量安全多方计算具体方案的隐私保护强度;3)为达到实际安全多方计算方案实用性与隐私性之间的平衡,需要对计算过程中的成本进行量化,本文提出计算目标函数需要付出的额外通信和计算开销来衡量隐私保护成本.

1 相关工作

目前,隐私度量的研究主要集中于特定的隐私计算领域如位置服务、社交网络和数据挖掘等.王彩梅等人[3]提出基于信息熵度量匿名通信系统的隐私度量方法.其他方案主要是为特定协议[4-6]量身定做的简单概率模型的隐私度量方法.另外一些方案[7-9]则是使用形式化的方法提供更高层次的抽象和更严格的匿名分析.

彭长根等人[10]于2016年提出基于Shannon信息论的几种隐私保护信息熵模型.隐私保护基本信息熵模型是将发送方拥有的信息集称为隐私信源,将接收方获取的信息集称为隐私信宿,隐私的泄露渠道假设为通信信道.该方案主要研究在隐私保护机制不泄露隐私信息的前提下攻击者通过隐私通信信道获取隐私信息的隐私度量方法.

上述研究主要针对匿名性和位置隐私保护等信息发布场景的隐私保护度量,这些应用场景只对隐私信源信息进行一次隐私保护处理,且隐私保护处理过程固定.然而,在安全多方计算或者隐私计算[11-12]的应用场景下,各参与者之间进行多次交互所联合实现的任务可以是任意的目标函数.因此,上述模型未充分考虑信源与信宿之间具有多次交互或者计算函数为任意函数的复杂情况.

衡量安全多方计算目标函数对特定参与者的输入信息的隐私保护能力的另一个角度是密码分析.密码分析技术是测试函数安全强度的最有力工具.可将目标函数的隐私度量看作一种密码分析.对于MPC的计算函数z=f(x,y),x由参与者P0输入,y由参与者P1输入,计算结果z由参与者P0获取.计算函数可转换为布尔函数的正规型表示,输入和输出以比特形式表述,可将函数f(x,y)视为加密函数,输入x视为明文消息,输入y视为密钥,输出z视为密文.由多个明文和密文对以及加密函数f()分析密钥信息的过程是典型的“选择明文攻击”.

目前,安全多方计算主要包括使用姚氏混淆电路[1]、秘密分享技术[13]、同态密码技术[14]等进行安全计算一个目标函数的方案.这些方案的设计更关注目标函数计算过程的安全性,却忽略了目标函数的输入及输出本身所带来的隐私信息泄露.Lindell[15]指出确保目标函数不泄露输入信息是隐私计算得以应用的隐含前提条件.

2 理想多方计算隐私度量方法

对函数f(x1,x2,…,xn)=(y1,y2,…,yn),具有n个参与者P1,P2,…,Pn进行联合计算,P1持有输入x1,P2持有输入x2,…,Pn持有输入xn,所有输入的定义域是公开的,除此之外,每个参与者无法获得与其他参与者的输入相关的任何信息;所有参与者都无法获得关于函数计算过程中的任何信息(如由一个可信的中心收集各个参与者的输入,再执行运算,最后将相应的计算结果发送给相应的参与者,可信中心不会与任何参与者共谋);函数计算结束后,每个参与者获得既定的计算结果,P1获得输出y1,P2获得输出y2,…,Pn获得输出yn,每个参与者无法获得关于其他参与者输出的任何信息.

上述情况是多方计算的理想情况,各方均不会从计算过程中获取任何其他的信息,可信中心也不会向任何一方泄露更多信息,在这种情况下,1个参与者想要攻击其他参与者只能通过其自身的输入和输出以及目标函数的性质完成.

对上述函数f(x1,x2,…,xn)=(y1,y2,…,yn),为适应计算设备的运算环境,假设函数的输入和输出均为离散的情况,设参与者输入的定义域分别为s1,s2,…,sn,x1∈s1,x2∈s2,…,xn∈sn, |s1|,|s2|,…,|sn|分别表示定义域中可能的输入值的个数;设参与者输出的值域分别为v1,v2,…,vn,y1∈v1,y2∈v2,…,yn∈vn,|v1|,|v2|,…,|vn|分别表示输出值域中可能的输出值的个数.

为简化模型的复杂程度,以下仅考虑两方计算的情况.多方计算函数可以简化成两方计算函数,对于多方计算函数f(x1,x2,…,xn)=(y1,y2,…,yn),可假定在最恶劣的情况下,其中n-1方参与者共谋以窥探其中1个参与者的输入和输出情况,那么共谋的n-1方参与者会获得彼此之间的输入和输出信息,此时模型则等价于上述两方计算模型,共谋的n-1方作为一个参与者,被攻击的一方作为另一个参与者.

对于只有两方参与的目标函数f(x1,x2)=(y1,y2),定义计算信息收益的概念,揭示在参与者P2的视角下参与者P1的特定输入x1对参与者P2的输出y2分布的影响程度.

2.1 平均熵

设目标函数f(x1,x2)=(y1,y2)的2个参与者分别为P1和P2,在理想的多方计算条件下(计算过程不泄露任何信息),参与者P2(攻击者)试图只通过其输入x2和输出y2分析参与者P1的输入x1或者输出y1.

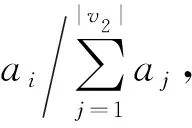
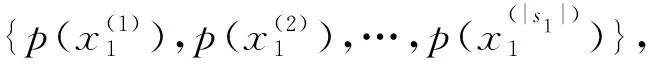
函数输出的平均熵H(f(P2,y2))体现所有输入对P2输出的分布影响.

2.2 特定熵

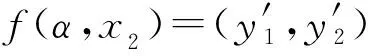
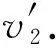
2.3 信息收益

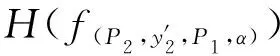
差值越大或者比值越大表明该特定输入对参与者P2的输出分布影响越大,参与者P2越容易从其自身的输出推断出参与者P1的值.

该定义可以理解为参与者P1有一个特定的数据x1=α与参与者P2共同计算函数f(x1,x2),参与者P2通过不断试探的方法,也就是遍历其输入x2获得额外的输出信息,以此推断参与者P1的输入情况.当参与者P2发现其输出熵严重偏离函数的平均情况(差值越大/比值越大)即可判定参与者P1的输入值.

3 安全多方计算的隐私保护强度

3.1 理想隐私损耗

目标函数f(x1,x2)=(y1,y2)的2个参与者分别为P1和P2,在理想的多方计算条件下(计算过程不泄露任何信息),定义“隐私损耗”的概念,揭示参与者P2通过其输入x2和输出y2推断出参与者P1输入x1的可能性.

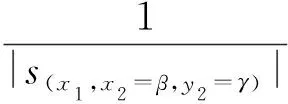
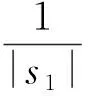
3.2 实际隐私损耗

在理想的多方计算场景下,各参与者仅知道各自的输入和输出,而不知道其他的任何信息,但在实际的安全多方计算实现方案中,如基于同态密码的委托计算、基于秘密分享的安全多方计算等方案中,各方在没有可信第三方的情况下使用基于密码或者信息论的安全措施进行数据的交换,计算结束后各方可以获得与理想情况下的相同的输出,但除此之外各方都会获得大量的中间交互信息.

实际的安全多方计算方案可以模型化为原目标函数经过一系列的等价变换最终获取与理想情况下的目标函数相同结果的过程.所谓等价变换指2种不同的运算过程对相同的输入都得到相同的输出结果.设在理想计算环境下,目标函数f(x1,x2)=(y1,y2) 的2个参与者分别为P1和P2,输入分别为x1和x2,相应的输出分别为y1和y2.设目标函数f(x1,x2)=(y1,y2)安全等价变换为f′(x1,x2)=fm(…f3(f2(f1(x1,x2),…),…),…)=(y1,y2),对相同的输入(x1,x2),安全多方计算函数f′(x1,x2)和理想情况下的目标函数f(x1,x2)输出相同的结果(y1,y2).

安全多方计算函数f′(x1,x2)由m个中间函数f1(),f2(),…,fm()复合而成,每次中间函数运行结束后,各方均会获得相应的输出(y(1,1),y(1,2)),(y(2,1),y(2,2)),…,(y(m,1),y(m,2)),其中y(i,1)为第i个中间函数的参与者P1的输出,y(i,2)为第i个中间函数的参与者P2的输出;并且各方会根据前一个中间函数的输出重新构造对下一步中间函数的输入(x(1,1)=x1,x(1,2)=x2),(x(2,1),x(2,2)),…,(x(m,1),x(m,2)),其中x(i,1)为第i(1≤i≤m)个中间函数的参与者P1的输入,x(i,2)为第i个中间函数的参与者P2的输入.概括来讲,中间输入和输出等价于实际安全多方计算过程中各方通过交互所获得的数据并执行下一次运算的过程.参与者P1在整个安全运算过程输入数据视图变化为x1=x(1,1)→x(2,1)→…→x(m,1),输出数据的视图变化为y(1,1)→y(2,1)→…→y(m,1)=y1;参与者P2的输入数据视图变化为x2=x(1,2)→x(2,2)→…→x(m,2),输出数据的视图变化为y(1,2)→y(2,2)→…→y(m,2)=y2.

参与者P2固定输入x2=β和输出y2=γ时,第i个中间函数fi(…f3(f2(f1(x1,x2),…),…),…),1≤i≤m的隐私损耗为Li=L(x1,x2=β,y(i,2),fi(…f3(f2(f1(x1,x2),…),…),…)),定义其中最大的隐私损耗为安全计算方案f′(x1,x2)=fm(…f3(f2(f1(x1,x2),…),…),…)=(y1,y2)在参与者P2输入x2=β和输出y2=γ时参与者P1的输入x1的实际隐私损耗为L(x1,x2=β,y2=γ,f′(x1,x2))=max{Li|1≤i≤m}.

实际隐私损耗的意义为寻找安全方案执行过程中对隐私泄露最大的步骤,由于整个隐私保护方案f′(x1,x2)与目标函数等价,因此实际隐私损耗至少等于目标函数的理想隐私损耗.

3.3 隐私保护强度

对一个目标函数f(x1,x2)=(y1,y2)和具体实现该目标函数的安全计算方案f′(x1,x2)=fm(…f3(f2(f1(x1,x2),…),…),…)=(y1,y2),定义该安全计算方案在参与者P2输入x2=β和输出y2=γ时的隐私保护强度为目标函数的理想隐私损耗与安全计算方案的实际隐私损耗之间的比值,即L(x1,x2=β,y2=γ,f(x1,x2))-L(x1,x2=β,y2=γ,f′(x1,x2))或者L(x1,x2=β,y2=γ,f(x1,x2))/L(x1,x2=β,y2=γ,f′(x1,x2)).

隐私保护强度体现安全多方计算方案对目标函数在计算过程中所造成的额外隐私泄露情况,相对于在理想运行环境下目标函数自身特性对输入数据隐私的保护,一个安全的隐私计算方案其安全强度越高(越接近1)越接近理想的运行条件,其计算过程所造成的额外隐私泄露越少.

4 安全多方计算的隐私保护成本

隐私保护成本是实现目标函数的安全计算函数比理想运行情况下(存在可信中心的情况)计算目标函数需要付出的额外通信和计算开销,表示为获得隐私保护所需要付出的代价.

对于中心化的多方计算目标函数f(x1,x2,…,xn)=(y1,y2,…,yn),其通信开销至多为2n次,即各方将输入发往可信中心并各自接收可信中心发来的输出.其计算开销即为可信中心在本地执行函数f(x1,x2,…,xn)的所需时间函数T(f(x1,x2,…,xn)).

对实现目标函数f(x1,x2,…,xn)=(y1,y2,…,yn)的安全计算方案f′(x1,x2,…,xn)=fm(…f3(f2(f1(x1,x2,…,xn),…),…),…)=(y1,y2,…,yn),其通信开销至多为2mn2次数据传输,也就是各方在每次执行中间函数的过程中都需要相互之间发送和接收数据.其计算时间开销为T(f′(x1,x2,…,xn))=n·{T(f1(x1,x2,…,xn))+T(f2(…))+…+T(fm(…))},n方参与者均需要在本地执行相关计算.

隐私保护成本如下:额外的通信开销为2mn2-2n次数据传输,额外的计算开销为T(f′(x1,x2,…,xn))-T(f(x1,x2,…,xn)).

因为达到理想情况下的隐私保护强度会引发通信花费大、计算消耗多等问题,所以实际隐私损耗和计算成本都不是越小越好.在实际应用中,需要综合考虑隐私保护成本和隐私度量情况评估安全多方计算方案的实现,达到方案实用性与隐私性之间的平衡.

5 结 语

随着学术界、工业界对安全多方计算越来越重视,实际应用的落地需求越来越强烈.此时,度量目标函数本身、安全多方计算方案组合及工程优化过程中的隐私损耗的重要性日益突出.本文试图针对隐私计算领域提供参与者衡量方案安全性的框架,以此为基础对安全多方计算的实际应用可行性进行了量化评估.