基于NTRU密钥协商协议设计

郑鉴学 张道法 徐松艳 宋苏鸣

(北京遥测技术研究所 北京 100094)

如今,网络通信已经成为人们生活中交流通信的重要渠道.然而,在开放的网络通信环境下信息很容易遭到攻击者的攻击.相较于对称密码,公钥密码可以在不安全的信道上传输加密的信息.然而公钥密码的加解密计算复杂,速度比对称密码加解密慢得多,所以加密大量的数据还需使用对称密码.因此公钥密码用于解决在开放网络通信环境中建立双方通信会话密钥的安全性问题.密钥协商(key agreement, KA)就是在不安全的信道下让2个或多个用户计算共同的会话密钥进行安全通信.

1998年,Hoffstein 等人[1]提出了NTRU格的概念,设计了一个基于多项式环上的公钥密码体制,通常被称为NTRU加密体制.随后几年,这种签名、加密方案不断出现,但一直没有提出可证明安全的方案,直到2008年,Lyubashevsky等人[2]、Gentry等人[3]先后提出了2个可证明安全性的格基数字签名方案.因此,基于格基上的公钥加密和数字签名技术取得了巨大的进步[4],然而基于格的KA(lattice-based KA, LBKA)协议目前仍然没有很好的发展.

由于KA协议在不安全的网络环境中运行,因此,设计出能够抵御各种攻击的认证KA协商协议就显得尤为重要.目前,BR,mBR,CK,eCK,seCK[5-8]都是密钥协商协议常用的安全模型,基于安全模型的密钥协商方案也在不断地发展[9-10].

在文献[11]中,将dA=(fA+prAcB),dB=(fB+prBcA)作为协商双方交互的信息,其中fA,fB分别为Alice和Bob的私钥,属于固定数据.该方案并没有对用户的私钥进行伪随机性保护,这给敌手攻击预留了方便.受此启发,本文对文献[11]进行改进,提出了2个基于NTRU格上的密钥协商协议.方案1中,本文在双方协商交互的过程中增加了2个随机化因子(r1A,r2A)和(r1B,r2B),使得参与密钥协商过程的发起方和响应方每次生成的会话密钥和协商的信息都不相同,保证了在密钥协商中会话密钥与随机序列的不可区分性.方案2中,本文利用NTRU加密方法,把双方随机选取的多项式(r1A,r2A)和(r1B,r2B)进行加密,得到dA=(r2A+pr1AcB)和dB=(r2B+pr1BcA)发送给对方,双方收到dA和dB后再对消息用自己的私钥进行解密.该方案密钥协商的过程中双方交互的消息都不包含各自的秘密信息(私钥),安全性完全依赖于NTRU加密方案的安全性,如果NTRU加密方案是安全的,那么该密钥协商方案在基于格上最短向量计算困难性SVP假设下会话密钥也同样具有不可区分性和不可伪造性.

1 相关知识描述

本节将介绍后续需要用到的关于格和NTRU格的一些基本知识,包括格的基本的定义、NTRU密码体制的基本思想及其困难性.

1.1 NTRU算法描述

NTRU加密系统取决于3个整数参数(N,p,q)和4个阶为N-1的系数是整数的多项式集合Lf,Lg,Lφ,Lm.注意p和q不需要是素数,但是本文假设gcd(p,q=1),并且设q≫p.本文的运算在多项式环R=[x]/(XN-1)上进行.1个元素f∈R可以写成多项式或者向量:

取2个元素f,g∈R,将符号⊕定义为环R上的加法运算符号,加法运算定义为

f⊕g=h,hk=fk+gk,

其中h∈R,hk为多项式h的k阶系数.

将符号⊗定义为环R上的乘法运算符号.乘法运算定义为

f⊗g=h,

其中hk为多项式h的k阶系数.容易验证R在以上定义的加法运算和乘法运算下构成1个环.进行1次模q的乘法运算,这意味着将多项式中的系数约简在模q下.

1.2 格

定义1.NTRU格.令q为大于5的素数,n为2的幂次,多项式f,g∈R(且f模q是可逆的).令h=g/f(modq),则由多项式h和q确定的NTRU格定义为

Λh,q={(u,v)∈R2|u+v×h=0(modq)}.

由定义1可知NTRU格Lh可以通过下面的2N×2N阶矩阵生成:

由生成矩阵可知,NTRU格为满秩格,NTRU格的行列式由素数q和2N维数唯一确定,即

det(Lh)=qN,

Λh,q是2N上的一个满秩格,Λh,q中的元素通过(v,r)Lh的行向量生成,其中r∈R.

2 方案设计和安全性分析

结合文献[12],本文对文献[11]的工作进行修改,提出2个密钥协商方案.

2.1 方案1描述

2.1.1 方案的参数选取

公开参数(N,p,q),其中选取N=251,p=3,q一般为2的幂次,可以取q=128或者q=256;多项式[x]/(xN-1)和[x]/(xN-1),其中:和分别代表有理数环和整数环;商环q[x]/(XN-1)和p[x]/(XN-1),其中模q运算的结果在[-q/2,q/2]内,而模p运算的结果在{-1,0,1}中.L(a,b)代表多项式环[x]/(XN-1)中的特定多项式的全体,这些特定的多项式有a个系数为1,b个系数为-1,其他系数为0.

2.1.2 密钥生成阶段

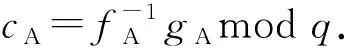
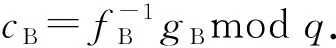
不妨取df=dg=dr=36,p=3.

2.1.3 密钥协商阶段

1) Bob随机选择2个多项式r1B,r2B∈L(dr,dr-1),计算dB=fBr2B+pr1BcA,并把dB发给Alice.

2) Alice随机选择2个多项式r1A,r2A∈L(dr,dr-1),计算dA=fAr2A+pr1AcB,并把dA发给Bob.同时计算

mA=r2AfAdB(modq)(modp),
SK=H(Key,dA,dB,IDA,IDB),

其中Key=r2Ar2BfAdB(modq).

3) Bob收到dA后,计算

mB=r2BfBdA(modq)(modp),
SK=H(Key,dA,dB,IDA,IDB),

SK作为Alice和Bob的协商密钥.

2.1.4 密钥协商的正确性

q取值为256时,p=3,而df和dg皆为36,故q>2p×max{df,dg}.

mA=r2AfAdB(modq)(modp)=
r2AfA(fBr2B+pr1BcA)(modq)(modp)=
(r2AfAfBr2B+pr2Ar1BgA)(modq)(modp)=
(r2AfAfBr2B+pr2Ar1BgA)(modp)=fAfBr2Ar2B,

同理mB=fAfBr2Ar2B,mA=mB=Key.

值得注意的是,由于r2A和r2B分别由用户随机选择,在线路上不传输,故第三方无法获取r2A和r2B,进而第三方也就无法得到mA和mB以及Key,进而提升了密钥协商数据的安全性.

2.1.5 对文献[11]的分析

文献[11]提出的NTRU-AKA协议中以下2点值得注意:

1) 文献[11]的密钥协商过程中:

dA=(fA+prAcB),dB=(fB+prBcA),
Key=mA=fAdB(modq)(modp)=
fBdA(modq)(modp)=mB=Key.

而fA,fB分别为Alice和Bob的私钥,属于固定数据.在双方交互的过程中,Alice和Bob分别发送了dA和dB,而dA和dB这2个消息中,文献[11]并没有对用户的私钥进行伪随机性保护,这给敌手攻击预留了方便,因此文献[11]只具有弱前向安全性,不能达到完美的前向安全性.

本文提出的方案1在密钥协商过程对发送的消息进行改进:

dA=(fAr2A+pr1AcB),dB=(fBr2B+pr1BcA),

其中(r1A,r2A),(r1B,r2B)∈L(dr,dr-1)是Alice和Bob分别选择的随机多项式.因此在每次的密钥协商中dA和dB中都没有直接使用Alice和Bob的私钥固定值.即使双方的长期私钥泄露也不能破解会话密钥.

2) 在文献[11]中并没有对其设计的NTRU密钥协商方案进行详细的安全证明.在2.2节中本文给出了在eCK模型下的安全方案及安全性证明.

2.2 方案1的安全性证明

2.2.1 eCK模型

敌手模型:A是拥有概率多项式计算能力的预言机,它能够全面监控网络,并且能够实现窃听、延迟、重放和篡改信息,同时还能够执行多项式数量界的询问.包括:

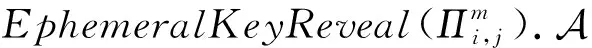
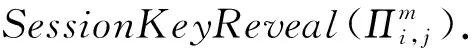
StaticKeyReveal(IDi).敌手获取身份为IDi的参与方i的私钥(fi,gi).

EstablishParty(IDi).敌手能模拟参与者i注册1个合法用户的身份IDi,并且可以获取其长期私钥.

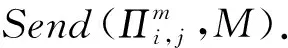
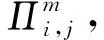
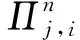
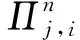
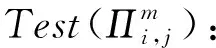
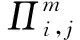
eCK安全性:1个2方认证密钥交换协议是安全的,如果它满足如下条件:

2.2.2 安全性证明

令k表示安全参数,A定义为1个关于k的poly(k)敌手.假设游戏中,A最多能够让nq(N)个不同的诚实参与方进行安全实验(敌手A可进行np(N)次StaticKeyReveal询问),每个参与方最多能参与np(N)个会话(敌手A可进行np(N)次EphemeralKeyReveal和SessionKeyReveal询问),A至多进行n0次H询问.如果A能够以1/2+f(k)的概率优势获得安全实验游戏的胜利,其中f(k)是不可忽略的,则A就有不可忽略的概率获得成功.H询问都被看作随机预言机,执行Test查询(成功概率为1/2).

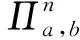
挑战者将利用赢得伪造攻击的敌手A构造求解器CH,以不可忽略的概率成功求解SVP问题.

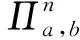
Setup:CH按照以下步骤建立系统公钥和用户长期私钥.

CH随机选择fi∈Lf(df,df-1)和gi∈Lg(df,df-1),设置(fi,gi)为第i个剩余参与方i的私钥i≠b.

Queries:A模拟poly(k)次的除Test查询外的其他询问,并将所有哈希函数看作随机预言机.A只询问1次Test查询.对于A进行的询问,CH对每个询问都有初始空列表,需要进行维护.

StaticKeyReveal(IDi):如果IDi=IDa,CH中止.否则,CH查询Λusers返回(fi,gi)给A.

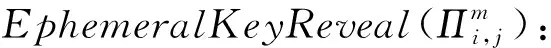
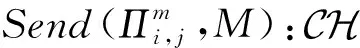
如果M是副本中的第2个消息,简单接受此会话.否则,考虑以下情形:

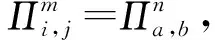
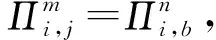
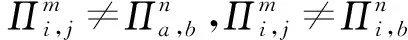
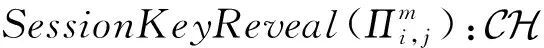
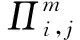
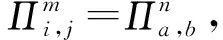
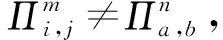
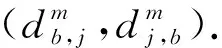
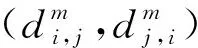
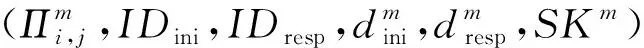
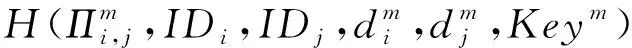
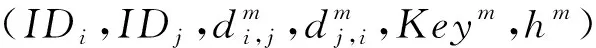
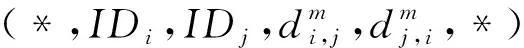
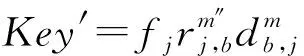
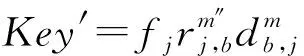
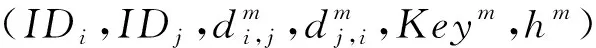
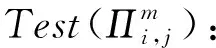
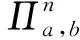
CH解决SVP问题的优势为Pr[CH成功]≥p1(k)/n0nq(N)2np(N),其中p1(k)为事件1发生并且敌手A成功伪造会话密钥的概率,即敌手A的优势.1/n0为n0次H询问发生碰撞的概率,1/nq(N)np(N)是在询问nq(N)np(N)次SessionKeyReveal询问后成功伪造会话密钥概率,1/nq(N)为nq(N)次StaticKeyReveal询问后成功伪造IDb的长期私钥的概率.因此如果敌手的优势p1(k)是不可忽略的,则CH解决SVP问题的优势也是不可忽略的.这与SVP假设矛盾.

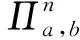
Setup:与事件1的询问类似.

Queries:CH参照事件1的实验回答除SessionKeyReveal以外的查询.关于SessionKeyReveal查询,CH回答如下:

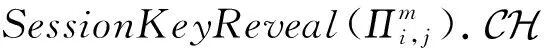
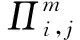
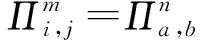
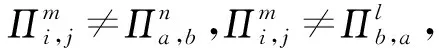
CH解决SVP问题的优势为Pr[CH成功]≥p2(k)/n0nq(N)2np(N)2,其中p2(k)是事件2发生并且敌手A成功伪造会话密钥的概率即为敌手A成功的优势.1/n0为n0次H询问发生碰撞的概率,1/nq(N)np(N)为在询问nq(N)np(N)次SessionKeyReveal询问后成功伪造会话密钥概率,1/nq(N)为在nq(N)次StaticKeyReveal询问后成功伪造IDb的长期私钥的概率,1/np(N)为在针对IDa的SessionKeyReveal询问中,成功伪造出匹配会话的密钥.因此如果p2(k)是不可忽略的,则CH的优势也是不可忽略的.这与SVP假设矛盾.

2.2.3 安全性分析

已知密钥安全:如果之前会话密钥泄露被敌手获取,他利用之前的会话密钥仍然不能解密本次会话密钥的任何信息.安全性实验中通过EphemeralKeyReveal查询,模仿敌手的已知密钥攻击.

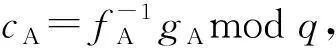
抗密钥泄露模仿攻击:如果敌手获取了用户A的长期私钥,敌手不能冒充A以外的用户与其他参与方进行通信.用户的公钥与其长期私钥息息相关,使得公钥和私钥一一对应,不能冒充.

前向安全性:1个或多个参与方长期私钥的泄露不影响之前建立的会话密钥的安全性.协商的会话密钥由双方的长期私钥和每次会话的临时密钥共同生成,即使双方长期私钥泄露也不能破解会话密钥,因此方案有完美前向安全性.

抗临时秘密密钥泄露:参与方临时私钥泄露并不影响利用此临时私钥进行会话的会话密钥的安全性.在安全证明实验中,利用EphemeralKeyReveal查询,模拟敌手获取参与方临时私钥的能力.

抗临时中间结果泄露:临时中间结果(即临时共享秘密值)的泄露不会影响该会话密钥的安全性(在不知道任何参与方长期私钥的情况下).在安全证明实验中,Send查询模拟了敌手可以截获密钥协商双方交互的信息.

2.3 方案2描述

方案2的密钥系统建立和密钥生成与本文的方案1类似.

2.3.1 密钥协商阶段

1) Bob随机选择2个多项式r1B,r2B∈L(dr,dr-1),计算dB=(r2B+pr1BcA),并把dB发给Alice.

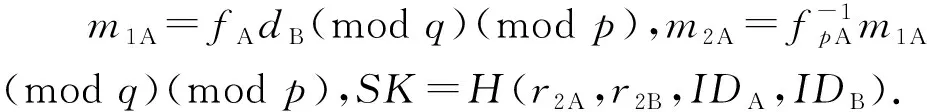
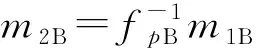
SK作为Alice和Bob的协商密钥.

2.3.2 密钥协商的正确性

q取值为256时,p=3,而df和dg皆为36,故q>2pmax{df,dg}.

m1A=fAdB(modq)(modp)=
fA(r2B+pr1BcA)(modq)(modp)=
(fAr2B+pr1BgA)(modq)(modp)=
(fAr2B+pr1BgA)(modp).

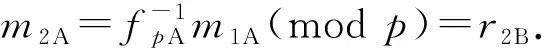
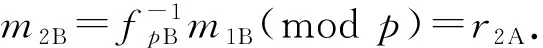
进而密钥协商数据SK可以在Alice和Bob之间保持一致.

分析:方案2的安全性证明和分析与方案1类似.由于r2A和r2B分别由用户随机选择,在线路上不传输,故第三方无法获取r2A和r2B,进而第三方也就无法得到mA和mB以及Key,进而提升了密钥协商数据的安全性.

方案2密钥协商的过程中双方交互的消息都不包含各自的秘密信息(私钥),安全性完全依赖于NTRU加密方案的安全性,如果NTRU加密方案是安全的,那么该密钥协商方案也是基于格上最短向量计算困难性假设(SVP)下会话密钥也同样具有不可区分性和不可伪造性.与文献[11]相比,减少了长期私钥泄露的风险,提高了安全性.

SK也可按如下方式计算:

SK=H(r2A+r2B,IDA+IDB),

这样可以让Alice和Bob处于平等地位.

3 与其他方案的对比分析

本文的2个方案是基于NTRU密码学构建的,相较于DH, ECDH等传统的密钥协商方案, NTRU方案基于多项式环上的运算效率更高,其安全性可以归约到求解格上的困难问题,可以抵御量子攻击.

将本文方案与其他方案进行比较.首先比较方案的计算代价,其中TE表示椭圆曲线密码学加解密的计算耗时,TNE,TND,TNM分别表示NTRU密码学加密、解密和多项式模运算的计算耗时.因为在NTRU加解密算法中多项式系数仅为{-1,0,1},分析文献[13-14]得到的NTRU加解密运算时间与分析文献[12]得到椭圆曲线加解密运算时间相比较,TE≫TNE,TND,TNM.NTRU密码运算效率和计算耗时远远优于椭圆曲线密码运算.其次,本文还分析方案是否具有完美的前向安全性(perfect forward security, PFS)和方案使用的安全模型,比较了各方案的安全性.比较的结果如表1所示:

表1 方案比较

基于NTRU密码学的方案1和方案2与文献[12]相比计算耗时少、效率高.文献[13]是基于BR安全模型设计的,没有分析临时私钥泄露后对方案的安全影响.文献[11]只能满足弱完美的前向安全性,如果临时私钥泄露还会降低用户长期密钥的安全性.本文基于更强安全性的eCK模型对文献[11]进行改进,本文方案1在信息交互中,对用户的私钥进行伪随机性保护,使得方案具有完美的前向安全性,虽然计算耗时增加,但是安全性更强;本文方案2对方案1进行了改进,提高了计算效率,计算耗时与文献[11]相当.

4 结 语

本文对文献[11]的认证密钥协商协议方案进行了改进,提出了一种基于NTRU格的密钥协商协议.在随机预言机模型下给出了详细的游戏模型,并证明了该方案在eCK模型中是可证明安全的.而现阶段,基于LWE和RLWE的加密方案[15]得到飞速发展,如何在安全目标不变的情况下找到计算量更小的LWE和RLWE的密钥协商协议是本文下一步的重点研究方向.