海底沙波对光缆铺设放缆余量计算的影响

周烨琦,王 锐

(1. 中英海底系统有限公司,上海 200240; 2. 上海交通大学船舶工程与建筑工程学院海洋工程国重点实验室,上海 210240)

1986年,全长120km的连接大加那利岛和相邻特内里弗岛的世界上第一条海底商用光缆建成。1988年,连通欧洲和美国全长6700km的海底光缆建成。之后海底光缆通信技术得到了蓬勃的发展[1、 2]。海底光缆的通信容量大、可靠性高、传输质量好,是现代国际通信的主要基础设施,承担世界上绝大部分互联网越洋数据和长途通信业务,在国际通信中起到重要的作用[3]。中国拥有绵长的海岸线长,且岛屿众多,大力开发建设中国沿海地区海底光缆通信系统,对于推动整个国民经济信息化进程、巩固国防具有重要现实意义。

海底光缆铺设时采用的余量不但关乎建设成本,而且决定建设质量。海底光缆按其所在的位置可分为岸端、浅海和深海3个部分。不同位置的水动力条件及受抛锚影响程度不同,铺设时放缆余量应该不同[4]。放缆量控制是光缆深海铺设准确性的重要手段[5]。如果没有足够的放缆量,光缆张力过大,光缆触底后无法紧贴海床轮廓,产生悬跨;如果放缆量过多,光缆太过松弛,触底光缆会出现绳套,光缆维修等产生的张力可能导致绳套出现扭结等故障。因此,须沿路由合理地分布放缆余量,以保证既紧贴海床轮廓不产生悬跨,也不出现绳套现象。从工程经验统计来看,海底光缆路由的平均放缆余量通常为3%～6%[4、 6],且由于海底光缆往往很长,放缆余量的变化范围很大,其具体的取值方法尚缺乏科学支撑。江伟等[6]针对深海光缆分析了海底光缆敷设施工余量控制的原理,将海底光缆余量分为区域余量、底部余量和释放余量,并提出了一种控制软件的操作流程和实施技术。郭俊宇等[7]通过模糊PID实现深海海缆定余量速度控制方法,当海底斜面角度发生大幅度变化时,可对设定余量进行自动修订,计算出符合当前船速、海底斜面角度施工的修订余量。但由于海底光缆的铺设通常应避开存在海底沙波运动的区域[4、 8],余量计算与控制不需要考虑沙波的影响,现有关于深海海缆铺缆余量的计算方法尚未考虑沙波因素。然而,沙波存在的区域往往范围广阔,如果避开它则显著增加光缆工程成本,有时,光缆路又别无选择地通过沙波海域。王伟平等[9]在对亚洲快线海底光缆香港段路由条件的调查中,发现大量沙波地貌,认为沙波移动会造成已铺设光缆的出露、悬空甚至移动等不良地质现象,危及光缆的安全,海缆的埋深和放缆余量需谨慎考虑。为此,本文将重点探讨海底沙波对光缆铺设余量计算影响等相关问题。首先,从海底沙波的成因、沙波床面上光缆受害的机理入手分析,进而得到可靠的光缆放缆余量计算方法。

1 海底沙波的成因及几何特征

1.1 海底沙波的成因

海底地形地貌非常复杂,底床泥沙在波浪或潮汐等水动力作用下会形成大范围的沙波。海底沙波在我国大陆架海域普遍存在,且深水沙波规模和分布范围往往比近岸浅水区的大得多[10],而海缆铺设时不可能完全避开沙波区域。为使海缆铺设时具有合理的放缆余量,保证其安全使用寿命,需要分析海底沙波的成因和几何特征,以得到合理计算放缆余量的方法。

由于海底洋流的存在,达到超临界状态的挟沙水流(弗汝德数Fr>1)会形成深水沙波的床面形态[11]。产生沙波有两个必要条件:

(1) 床面泥沙颗粒在水流的作用下可以产生运动,水体对底床的切应力τb必须大于底床颗粒运动的临界切应力,即:

τb>θcr(γs-γ)d50

(1)

式中,θcr为底床泥沙颗粒粒径d50对应的起动希尔兹数;γs为底床泥沙的容重,N/m3;γ为水的容重,N/m3;d50为底床泥沙中值粒径,即小于该粒径的颗粒占沙样总重量的50%,m。

通常,能起动床面泥沙颗粒的临底水流为紊流。依据普朗特紊流理论,其紊流切应力可以表达为

(2)

式中,τ为切应力,Pa;ρ为水体密度,kg/m3;l为掺混长度,m;u为流速,m/s;z为临底高度,m。

(3)

对于临近海底,假设底床上的切应力为τ0,水体掺混长度l=κz,κ为卡门常数。式(3)积分可得临底的流速分布遵循对数关系:

(4)

假设高出平均床面d50处的流速为0,则

(5)

将(5)代入(4)得:

(6)

因此,床面泥沙颗粒在水体作用下能够运动的条件是

(7)

(2) 底床泥沙颗粒运动必须以推移质运动形式进行,而非悬移质运动形式。参与沙波形态演变的泥沙必须在沙波的背水面淤积下来。如果泥沙起动后直接成为悬移质,则无法淤积在背水面。

1.2 海底沙波尺度

深海沙波的尺度与当地洋流大小及方向、海底坡度以及海底床沙质特性等因素有关,在砂质海床上往往出现不同尺度的沙波。对于均匀流环境,沙波的几何特征如图1所示。海底沙波的高度为Δ,长度是前坡长度lf和背面坡长度ll之和L=lf+ll。平均而言,前坡长度lf是背面坡长度ll长度的3倍[8],即lf=3ll,ll=L/4。

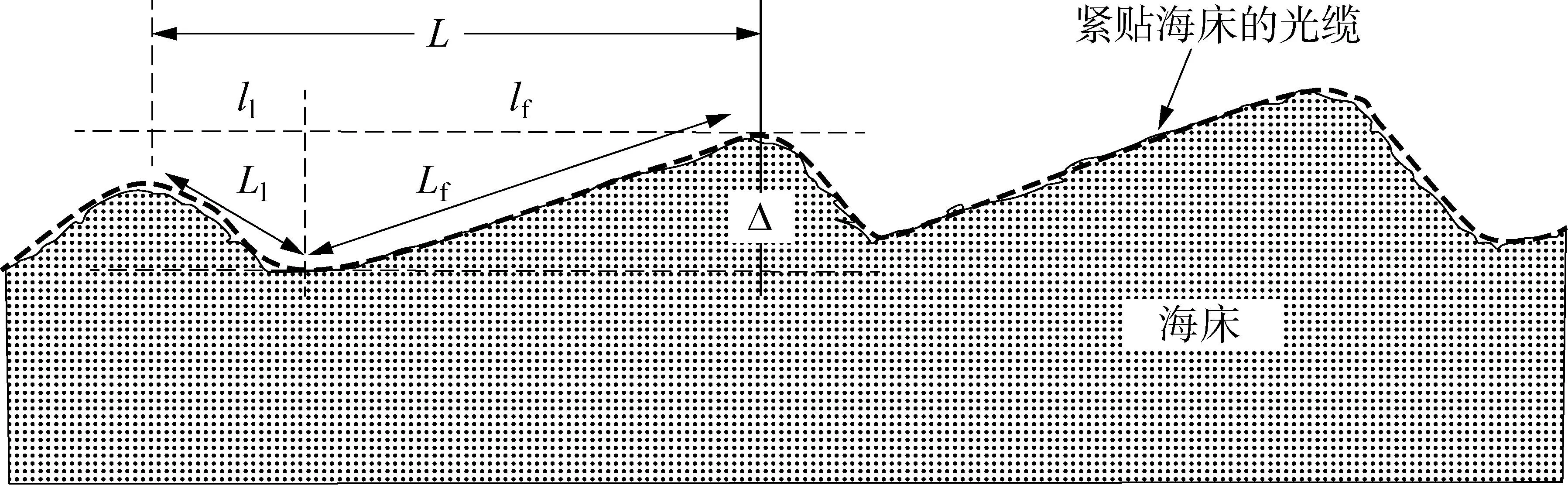
图1 沙波的几何特征

在海洋环境下,Maselli等[12]观察东地中海黎凡特盆地(Levant Basin)海底,发现大范围不对称沙波,如图2所示。一类是新月形的沙波,波高35～50m,波长830～1465m,背流和迎流面的坡度分别为12.2°～23.7°和4.1°～6.4°;另外一类有轻微弯顶部平行分布的沙波,其波高5～30m,波长910～1670m,陡度大于50,背流和迎流面的坡度分别为7.3°～2.6°和3.6°～0.5°。在我国南海和台湾海峡附近均存在大范围的大尺度海底沙波,在东沙群岛和台湾岛水深2100～3000m的海底存在波长为1.3～3.5km、波高为10～77m的沙波[13]。在南中国海的北部发现了东沙西沟、西台湾海峡、南台湾海峡和澎湖西沟4个沙波区域,波长可达2.8～7.2km,波高可达30～60m[14]。当波峰与海沟方向正交或倾斜时,无论是在下坡方向还是随着离海沟距离的增加,泥沙波的尺寸都会逐渐减小。目前,尚缺乏对深海沙波尺度的理论研究,预测深海沙波只能采用明渠均匀流条件下沙波尺度计算公式。

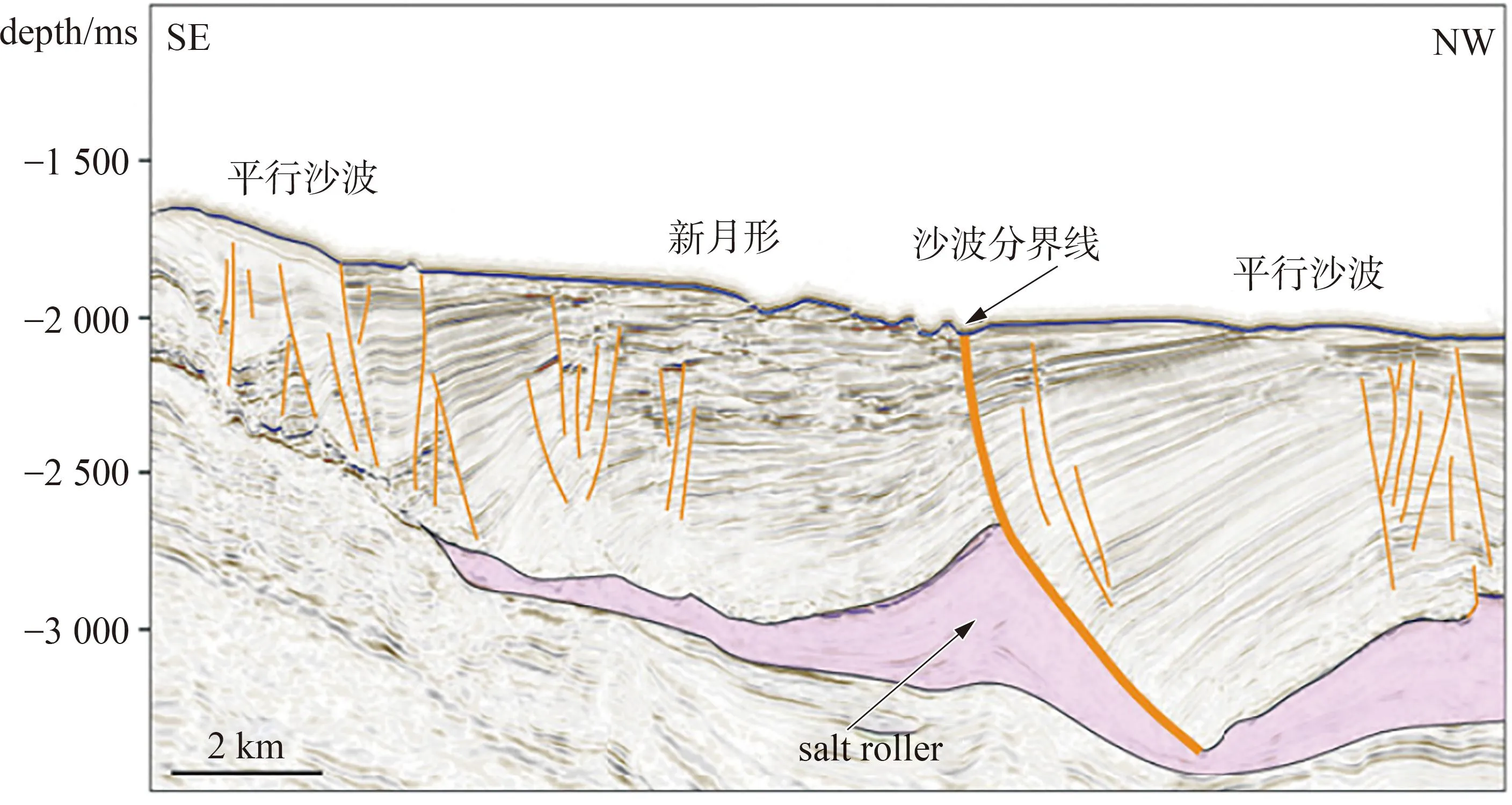
图2 Levant Basin海底的沙波分布

在均匀流条件下沙波尺度计算方面,国外的代表性学者Van Rijn对水深大于0.1m的84组美国水道试验站等完成的实验数据(泥沙粒径0.190～1.35mm)和22组野外数据(泥沙粒径0.35～3.6mm)进行了回归分析,提出沙波高度和长度的计算公式[15]:

(8)

(9)

式中,T为泥沙的状态参数,H为水深,m。

(10)

其中,Δ为波高,m;λ为波长,m;H为水深,m;U′*为沙粒摩阻流速,m/s,U′*=(g0.5/C′)×U,而C′=18log(hb/d90)为谢才系数,U为近底平均流速,m/s;U*cr为泥沙起动的临界摩阻流速,m/s;d90为累计粒度分布数达到90%时所对应的颗粒粒径,m。

在国内,代表性成果为武汉水利水电学院给出的公式[16]:

(11)

值得注意的是,上述公式在推导过程中采用的实验水深较浅,底床的相当光滑度(H/d50)小,沙波尺度的发展受到抑制。而海洋中的水深相对河道而言则大得多,沙波尺度得到更多发展空间。鉴于床面上流速分布是底床切应力的决定要素,以及海洋临底流速和明渠流平均流速分布的相似性,上述公式中的水深应该取海洋近底层的边界层厚度,而非全海水深。动量边界层的计算公式[17]如下:

(12)

其中,η为动量边界层厚度,m;η*为边界层厚度,m;d为底床颗粒泥沙粒径,m。在水槽试验或天然浅水试验中,边界层厚度一般由流动深度决定,η*=H。

2 光缆长度余量分析

2.1 沙波上铺设光缆的放缆余量计算方法

光缆的放缆余量P以百分比表示如下:

(13)

式中,Ib为某一时段内的海底光缆布放长度,m;Is为该时间内的海缆施工船只航行的距离,m。

铺设在深海海底的光缆须完全贴合在海床上。因此,一个完整沙波上铺设光缆的最小长度应为

(14)

式中,c1、c2分别为前坡的形态系数和后坡的形态系数。对于对称正弦波型沙波,c1=c2≈1.3。如果两波峰之间的放缆量小于L1,则在两个相邻波峰之间,海底光缆触底后无法紧贴海床上的沙波坡面而悬空。洋流和内波的不断作用导致悬跨的光缆涡激振动,最终导致材料疲劳而失效。这种往复振动促进光缆底下海床泥沙的流化,增大水流对光缆的淘刷能力。两个波峰间光缆悬空,临底的高浓度悬移质泥沙不断流过光缆,时刻产生磨蚀,缩短光缆安全寿命。因此,沙波对光缆余量的增量应该为

(15)

将lf≅3ll代入上式可得

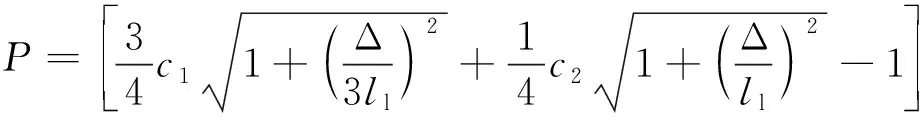
(16)

利用泰勒级数展开:

(17)

(18)

近似地,c1=c2=C。则沙波对光缆放缆余量的增量应为

(19)

(20)

将ll=L/4及C=1.3代入上式,得

(21)

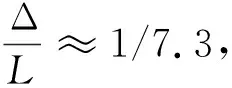
2.2 放缆余量计算方法的应用

不同大洋海底,由于洋流大小、方向不同,海底底质不同,以及海底坡度的变化,沙波的高度与长度会随时空而不断发生变化,放缆余量百分比也将不同。例如,在南中国海的北部发现了东沙西沟、西台湾海峡、南台湾海峡和澎湖西沟4个沙波区域,波长可达2.8～7.2km,波高可达30～60m。为消除沙波段的悬空,平均放缆余量应该增加1.3%。东地中海黎凡特盆地(Levant Basin)的新月形沙波,波高35～50m,波长830～1465m。为消除沙波段的悬空,平均放缆余量应该增加3.7%～4.5%。可见,对于存在新月形沙波的海底,平均的放缆余量宜大于3%。

由上述分析可知,大洋海底的大尺度沙波运动危及海缆的安全,大尺度沙波的陡度是影响光缆铺设放缆余量的重要因素,计算光缆铺设放缆余量必须考虑大尺度沙波的影响。另外,光缆铺设放缆余量计算采用了动量边界层厚度代替水深,提高了计算的精度和降低光缆铺设时经过沙波存在区域时的风险。

3 结 论

本文在海底沙波尺度分析光缆铺设长度的余量影响,通过理论推导得出如下结论:

(1) 为消除沙波隆突而造成的光缆悬空引发的疲劳破坏等问题,光缆铺设时必须增加光缆铺设长度的余量。

(2) 沙波对光缆铺设长度的余量可按公式(21)计算。其中,沙波高度和长度的计算公式(8)、(9)及(11)供参考;在光缆工程设计时,高精度的海底沙波尺度观测与分析非常重要。

(3) 新月形沙波的海底光缆的放缆余量应大于3%,其他类型沙波的海底光缆的放缆余量应大于1.3%。