特征扰动频率辨识的自适应倾斜扰动抑制技术
吴红梅,王 琛,冯 念,文 利,唐 涛*
1 中国科学院光场调控科学技术全国重点实验室,四川 成都 610209;
2 中国科学院光束控制重点实验室,四川 成都 610209;
3 中国科学院光电技术研究所,四川 成都 610209;
4 中国科学院大学,北京 100049;
5 航天系统部装备部军事代表局驻成都地区军事代表室,四川 成都 610000
1 引言
倾斜校正系统广泛应用于高分辨率望远镜、自由空间光通信等精密光学系统中,实现稳像、光束稳定等功能[1-2]。如在望远镜中,倾斜校正系统进行稳像时会受到扰动的影响,其中引起光束抖动的扰动普遍具有未知性和时变性[3]。因而抑制倾斜校正系统中的时变扰动对于提升光学系统视轴稳定精度至关重要。目前,倾斜校正系统中抗扰方法主要集中在比例积分(PI)控制、扰动前馈(DFF)控制和扰动观测器(DOBC)控制[4]。王等人提出基于SBG 的双扰动捷联控制进行抗扰,提升稳定精度。张等人提出一种新型控制方法,该方法既能进行隔振抗扰,又能进行高精度跟踪[5-6]。但是这些方法对扰动的抑制能力有限,难以抑制时变随机扰动。为了抑制倾斜校正系统中的时变扰动,许多自适应控制方法被提出。张等人在光电稳像平台中提出了无迹卡尔曼滤波扰动力矩在线估计方法,结合前馈控制对于扰动力矩进行自适应补偿[7]。在望远镜中,有研究者针对时变扰动提出了基于频谱分离和优化算法的LQG控制,该方法在抚仙天文台的望远镜系统中得到验证,并证明了系统在线识别性能的实时性[8]。但是这两种方法需要精确的建模,这是一个耗时的过程。因此为了进一步提高稳像性能,阮等人提出基于在线功率谱密度估计的自适应Youla 参数化控制,实现对一个或多个变化扰动的实时抑制,并且该方法不依赖精确的模型[9]。在其它高精度控制系统中,有采用基于频率分离的自适应前馈控制和基于状态观测器的自适应滑模控制对时变扰动进行抑制[10-11]。由上述方法可知,自适应控制的核心是参数辨识算法和控制结构。参数辨识是对扰动信号的频率、幅值、相位等特征进行辨识[12-13]。目前辨识算法多数基于频谱分析,如基于DFT、FFT 等的估计方法。这些自适应控制算法是全频域搜索,计算量大、耗时较长[14-15]。另一类自适应算法从时域对特征扰动频率进行估计,对实际采集到的信号基于最小均方(LMS)算法进行降噪,再提取主峰频率估计值[16]。Yuan 等人为抑制波浪扰动的影响,提出基于最小二乘辨识算法对波峰频率进行估计,最后仿真结果表明能对波峰频率进行准确估计[17]。由于LMS 算法计算复杂度不高,近年来有较多基于LMS 算法的自适应陷波频率辨识方法的研究。如文献[18-19]等采用自适应陷波的方法对扰动频率进行估计,较为简单和快速。
如上所述,在倾斜校正系统中进行时变扰动抗扰时,多数自适应控制算法进行的是全频域的搜索方式并且需要精确的建模,参数辨识部分的算法计算量大,调整的控制器参数较多,复杂且耗时。然而基于Youla 参数化控制的自适应算法不依赖精确的模型,可以直接调整控制器的内模,降低了自适应控制器的复杂度,不涉及对控制器进行复杂的重新设计。同时基于Youla 参数化的控制方法是一种优化误差的方法,能保证动态闭环系统的渐进稳定性[20-21]。从辨识算法来说,基于LMS 的时域辨识算法简单、快速,为控制器参数的快速调整提供了保障。因此,本文提出一种基于LMS 的特征扰动辨识与Youla 参数化控制结合的自适应扰动抑制方法,以提高自适应扰动抑制的速度,提升倾斜校正系统的闭环性能。
2 倾斜校正系统自适应控制
在倾斜校正系统中,利用传统的控制方法进行闭环控制后系统中仍然存在两种扰动难以抑制。这两种扰动主要表现为幅值小、频带宽的扰动和大幅度窄带扰动。为此Ruan 等人采用Youla 参数化控制,将控制器F(z)分为低通滤波器和带通滤波器两部分,对低频扰动和大幅窄带扰动进行抑制。此结构简单且易于保持系统稳定性,但是该方法不能应对时变扰动[22]。因此本文基于频率分割将带通滤波器设计为自适应控制器Q(z),以应对时变的大幅、窄带尖峰干扰。同时兼顾了低通滤波器的优势,能对低频扰动和大幅窄带扰动进行抑制。倾斜校正系统是基于图像闭环的控制系统,如图1 所示,由中心控制器、扩展控制器、驱动器、倾斜镜、图像传感器组成。其中图像传感器用于检测目标质心,以提供受控的倾斜误差。在扩展控制器部分本文提出利用自适应算法对特征扰动的主频信号进行在线快速辨识,调节自适应控制器Q(z)的参数,与中心控制器共同衰减倾斜误差。

图1 自适应倾斜校正系统Fig.1 Adaptive tip-tilt correction system
如图2 所示,为本文所提出的自适应Youla 参数化控制结构,该控制方法的自适应部分将Youla 参数化控制与自适应频率辨识相结合。如图1 所示,由于光路中和平台带来的扰动会影响闭环误差,因此频率在线辨识部分对闭环误差e(k)进行估计,用估计所得的参数对控制器Q(z)进行调整。中心控制C(z)是传统的比例积分控制,M(z)为低通滤波器。将控制器Q(z)与低通滤波器M(z)合并为扩展控制器K(z),则该控制结构的扰动抑制函数为
式中:K(z)=Q(z)+M(z),P(z)是等效被控对象特性,z-n是系统延时,z-m为等效延时。原始闭环反馈控制系统的扰动抑制函数D′(z)=。若获得系统模型与系统延时,则有:
此时D′′(z)=[1-K(z)z-m]D′(z),因此若要提高系统扰动抑制能力,即实现 1-K(z)z-m的最小化。在理想情况下,当 1-K(z)z-m=0时,闭环误差可以被完全消除。但只有在中低频条件下才较容易获得系统模型,所以扩展控制器K应为一个低通滤波器,使接近于0。此时该控制系统的闭环传递函数为
其中:
由式(3)可得特征多项式为
式(5)满足小增益定理,可以保证系统的稳定性。
针对倾斜校正系统中高频扰动和低频扰动的抑制,利用频率分割的方法,控制器Q(z)与M(z)并联,K(z)=Q(z)+M(z)。当只有低频扰动时,M(z)为低通滤波器,此时 1-K(z)z-m表现为 1-M(z)z-m,整体呈现高通滤波效果,可以对低频扰动进行有效抑制且满足系统稳定性;对高频扰动进行抑制时,提高扰动抑制能力的主要任务是对自适应控制器Q(z)进行设计,即最小化 1-Q(z)z-m,以抑制时变的窄带尖峰干扰。
3 基于闭环误差的特征频率辨识
自适应倾斜校正系统中,对时变窄带尖峰扰动的中心频率进行快速辨识是自适应控制的关键。在频率辨识的方法中,最直接且准确的方法是进行傅里叶变换。如FFT 算法,但是傅里叶变换运算复杂,并且需要采取一定的数据点,耗时较长。因此,本文从时域出发提出基于闭环误差的特征扰动频率辨识算法,理论上只需获取三个数据点就能得到该时刻的频率辨识值。假设主导扰动为余弦信号S(k),则:
其中:I、ω、φ分别为未知闭环误差信号的幅值、角频率和初始相位。FS为采样频率,f为待辨识的扰动信号频率。对S(k)进行等间隔采样,再利用离散的相邻数据点S(k-2)、S(k-1)、S(k)求出关于扰动信号频率的方程。根据三角恒等变换cosα+cosβ=可得:
然而在实际系统中,待辨识信号混杂了噪声,这对于所取数据点具有很大的影响。直接采用式(7)难以准确获取特征扰动频率。为了最小化估计误差,对时变窄带尖峰扰动的中心频率进行准确辨识,采取如下处理,假设实际信号为V(k),则有:
由式(8)可得:
γ=2cosω,为本文的特征扰动频率辨识参数。
采用LMS 算法,建立如下优化目标函数:
此时目标函数梯度为
根据梯度迭代搜索公式可得 γ的下一时刻更新值:
由于在倾斜校正系统中是对闭环误差信号e(k)进行估计,因此式(13)变为
其中,ζ=2µ为步长因子且ζ>0。结合式(9)、(14)获得 γ,其中步长因子 ζ的选取十分重要。由式(9)知γ=2cosω,则ω=arccos(0.5γ),因此:
当系统采样频率为2000 Hz 时可得:
由式(16)可得出,步长因子 ζ<0.0001,即 0<ζ<0.0001时,扰动中心频率变化小于1 Hz;步长因子 ζ<0.00001,即 0<ζ<0.00001时,扰动中心频率变化小于0.1 Hz。在此范围内ζ 越小,辨识越准确但收敛速度越慢;ζ 越大,辨识速度越快但会导致辨识准确度变差。因此,在工程应用中应考虑辨识精度以及实际系统噪声等因素选择合适的步长[23-24]。
4 自适应控制器Q 的设计
在倾斜校正系统中实现自适应控制包括两个重要部分,分别为参数辨识和自适应控制器的设计。参数辨识部分上一节进行了讨论,接下来是控制器的设计与参数调整。本文进行自适应控制时是以衰减闭环误差为目的。在进行参数辨识时采用式(9)、(14)结合,衰减误差值 δ(k),逼近特征频率相关参数 γ的值。因此在进行自适应控制器设计时也采用与式(9)类似的数字陷波器,二者保持一致性,进而更新辨识部分参数时,也能同步更新自适应控制器的参数,以达到δ(k)与闭环误差衰减的一致性。本文所设计的自适应控制器如图3 所示,在原有低通滤波器M(z)的基础上并联自适应控制器Q(z),下面将对自适应控制器Q(z)进行详细设计。

图3 自适应控制器Fig.3 Adaptive controller
在第二节中提出提高扰动抑制能力主要是实现 1-Q(z)z-m的最小化,即最小化 1-Q(z)。令W(z)=1-Q(z),为抑制窄带尖峰干扰,W(z)应该被设计为一个陷波器,所以自适应控制器Q(z)应该被设计为一个峰值滤波器。本文采用的数字陷波器为
其中:C1=1,C2=2cos(ω0)是本文控制器的设计参数,ρ∈(0,1),为与陷波器的带宽和深度有关的参数。根据式(17)可以得出X(z,ω0)和T(z,ω0)的输出分别为p′(k)和p′′(k),表示如下:
式(9)和式(18)一样,因此在估计误差收敛时,自适应控制器的输出也实现同步收敛。p′′(k)作为本文进行特征扰动辨识时的估计误差观测值,实时反应误差收敛情况。自适应控制器表示为
控制器Q(z)的输出为
其中:b(k)为实际控制器输出信号,式中陷波器的输入为x(k),x(k)=。C2为经本文提出的基于最小均方误差准则的特征扰动频率辨识参数,最后对它进行调节。
本文采用的数字陷波器W(z),其幅频特性为W(ω),相频特性为 φ,则
其中:
如图4 所示,通过仿真可以直观看出该陷波器的频率特性。当参数 ρ越接近1 时陷波器带宽越小,陷波衰减特性越好;但是当陷波深度越深时,带宽较窄,对参数估计误差的容忍度较小。减小 ρ的值,陷波器的带宽会变大且深度还是很深,会影响系统稳定性。因此调节另一个参数C1,使它变为一个接近于1 的数。在C1=1.00001时,陷波器的深度会变浅。而C1=1.00001保持不变,ρ依次为0.985 和0.905 时,ρ为0.905 深度会更深。因此采取一个合适的值,本次实验所用参数C1、ρ分别为1.00001 和0.985。在实际工程应用中,可以根据自身需求去调节相应参数。

图4 不同参数陷波器的幅频特性曲线Fig.4 Amplitude-frequency characteristic curves of notch filters with different parameters
5 实验验证
为验证本文所提出的控制方案,搭建如图5 所示实验平台。TTM1 和TTM2 为音圈驱动的倾斜镜,实验过程中驱动TTM1 用来模拟加载平台振动产生的扰动,TTM2 可以模拟光路中带来的扰动。TTM3 是以压电陶瓷驱动的倾斜镜,该倾斜镜具有X、Y两个活动轴,闭环分辨率为0.05 μrad,角行程为2 mrad,作为被控对象。本实验只对TTM3 的Y轴进行控制,X轴是禁用的,扰动镜也一样。图像传感器PSD 用于获取光斑的位置信息。进行实验时由激光器发出光源,经过以压电陶瓷驱动的TTM3 再反射到TTM2,最后回到图像传感器检测目标位置信息。图像传感器PSD 的采样频率为2000 Hz,分辨率为1 μm,将PSD 采集到的信息传到闭环控制回路,对倾斜误差进行调控。

图5 实验平台图Fig.5 Experimental platform diagram
5.1 并联滤波扰动抑制
为验证本文提出频率分割方法中并联滤波的有效性,对PI 控制以及加入Youla 参数化控制结构时仅使用滤波器M(z),M(z)并联Q(z)的三种频率特性测试进行对比,并绘制了误差抑制曲线C、M、K。实验采用带宽为10 Hz 的二阶低通滤波器M(z),中心频率为20 Hz 的陷波器Q(z)。图6 所示,相比于PI 控制,使用低通滤波器M(z)以提高7 Hz 以下的扰动抑制能力,采用并联滤波后,如黄色曲线所示,系统的误差抑制能力进一步提升,所设计的并联滤波器对低频和高频的扰动抑制的有效性。

图6 三种情况下的扰动抑制能力曲线Fig.6 Disturbance suppression ability curves in three cases
5.2 单频时变扰动的自适应抑制
为验证控制器Q(z)对单频时变尖峰扰动的自适应抑制,进行了如下实验。其中扰动由TTM1 产生,输入倾斜校正系统的模拟扰动频率依次为23 Hz、30 Hz、35 Hz、42 Hz、48 Hz,单次扰动频率发生变化的间隔时间约为17 s。控制系统闭环后,通过在线自适应特征扰动频率辨识可以得到未知扰动的中心频率如图7 所示。图中标出了频率辨识的瞬时值与对每个扰动频率进行辨识的相对误差平均值,可看出相对误差不超过2%。本次实验过程中考虑辨识精度与实际噪声的因素,步长因子ζ 取值为0.0000001。在自适应扰动抑制过程中,辨识算法估计误差的观测值随时间的变化趋势如图8 所示,估计误差发生剧烈变化的时间较短,能快速收敛且趋于稳定。如图9 所示,红色曲线和蓝色曲线分别表示自适应控制方法和PI 控制方法下倾斜误差的变化趋势。且倾斜误差变化趋势与估计误差变化趋势一致,证明辨识的滤波参数与控制器调整并行化设计的有效性,以达到估计误差和实际倾斜误差的同步收敛。从频域图得出自适应Youla 参数化控制较PI 控制时,对扰动的抑制能力提高了2到3 倍。实验结果表明,当扰动频率发生变化时自适应控制器Q(z)可以快速有效地抑制变化的扰动。

图7 频率辨识过程Fig.7 Frequency identification process

图8 扰动连续变化时的估计误差Fig.8 The estimation error when the disturbance changes continuously
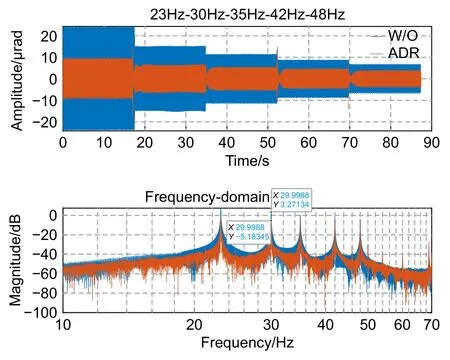
图9 扰动连续变化时倾斜误差的时域、频域图Fig.9 Time domain and frequency domain diagram of tip-tilt error when disturbance changes continuously
为了更直观地对比两种控制方法的抗扰性能,列出了此次两种控制方法的均方根误差如表1 所示。在本次连续发生5 次变频模拟扰动的实验中,自适应Youla 参数化控制算法对扰动的抑制率相比于PI 控制方法至少提升51.6%,平均扰动抑制率提升了58.7%。直观地表现了本文所设计的控制器Q(z)能自适应地对未知时变的尖峰扰动进行快速、有效的抑制,有效提升倾斜校正系统的性能。

表1 均方根误差Table 1 Root-mean-square error
5.3 多频扰动的自适应抑制
低频扰动和高频扰动同时存在或出现多个高频扰动时,倾斜校正系统面临更大的挑战。为了验证本文所提出的自适应Youla 参数化控制算法对主频扰动与低频宽带扰动的抑制能力,进行了两组多频混合扰动的实验,实验中扰动均由TTM1 产生。第一组实验输入频率为2 Hz、24 Hz 和50 Hz 的混合扰动信号。图10(a)为混频扰动信号输入系统时倾斜误差的时域频域变化图。蓝色曲线为PI 控制下的倾斜误差,红色曲线为自适应控制时的倾斜误差。该组实验中,2 Hz的低频扰动得到有效抑制,同时24 Hz 的主频扰动被衰减了8 dB 左右。采用PI 控制时,倾斜误差的均方根误差为15.49 μrad,进行自适应控制时为6.50 μrad。证明了控制器M(z)和自适应控制器Q(z)的有效性。第二组实验输入频率为10 Hz、20 Hz 和60 Hz 的混合扰动信号,如图10(b)所示,在多个尖峰扰动的情况下,主频干扰衰减约13 dB;自适应控制方法较于传统PI 控制方法,倾斜误差的均方根误差从19.29 μrad 衰减至5.12 μrad,证明了本文所提出的基于LMS 的自适应Youla 参数化控制算法能对主频干扰进行有效抑制。

图10 抑制多频扰动的倾斜误差。(a)低频宽带扰动混合尖峰扰动;(b)尖峰扰动Fig.10 Tip-tilt error of suppressing multifrequency disturbances.(a) Low-frequency broadband disturbance mixed spike disturbance;(b) Peak disturbance
6 结论
本文通过理论分析和实验验证,证明基于频率分割的自适应扰动抑制方法能对高频扰动和低频扰动进行有效抑制。所提出的自适应辨识算法采用最小均方误差准则,利用闭环误差进行特征频率辨识,能快速有效的抑制未知时变的尖峰扰动。该辨识算法与Youla 参数化控制相结合,在不影响系统稳定性的基础上,将扰动抑制问题转变为误差衰减的问题。与传统的闭环反馈控制相比,在单频时变扰动或多频扰动下均可有效提升系统的闭环性能。同时本文提出的算法不仅能应用在稳像系统中,也可用于其它高精度控制系统。后续研究中将着重对多个特征扰动频率进行辨识,实现对多个扰动的同时抑制,使倾斜校正系统性能得到进一步的提升。

