基于声学黑洞的水下航行器承压板减振设计及性能研究

马锐磊,白建斌,刘一鸣,田文强,田丰华,刘礼文

(中国船舶集团有限公司 第705 研究所,陕西 西安,710077)

0 引言

水下航行器一般通过位于头部的声学阵列进行探测,实现对目标及环境信息的感知。水下航行器在航行过程中,其后部的动力系统及尾部的螺旋桨会产生巨大的振动噪声(即航行器自噪声),经过壳体振动传递及声振耦合,对头部声学阵列形成很强的噪声干扰[1]。

自噪声直接影响目标信号的信噪比,是水下航行器实现目标探测与识别的主要干扰背景。自噪声分析结果表明,结构振动噪声是自噪声的重要来源之一。结构振动是在航行器壳体及内部组件间固固传递的振动形式,激励源主要包括动力系统、辐射噪声(声振耦合)及组件间相互作用等[2]。

承压板位于水下航行器头段内部,起到连接探测声学阵列和头段壳体的作用。在航行过程中,来自后部动力系统的振动噪声通过壳体及内部组件传递到承压板处,进而传递到声学阵列内,因此对承压板进行有效的减振设计十分必要[3]。目前在承压板设计过程中主要采用吸声、隔振材料来降低传递过来的振动能量。但是,由于吸声、隔阵材料的性能会随频率的降低而变差,虽对中、高频段噪声较为有效,但对低频噪声效果不大,迫切需要应用新的宽带减振技术。

声学黑洞(acoustic black hole,ABH)由于具有高效、轻质及宽频等特性被广泛关注。其基本原理是通过结构阻抗变化,相应改变结构中传播的波相速度和群速度,使能量在局部黑洞区域实现聚集。现阶段ABH 的研究主要聚焦在减振机理及提高ABH 效应等方面: Bowyer 等[4-6]通过实验方法测试了阻尼材料对非完美ABH 效应的补偿效果;Feurtado[7]和Ma 等[8]探究了自由场中ABH结构波数演变与辐射机制;O’Boy[9]和Bowyer[10]等研究了平台长度对ABH 效应的影响;Li[11]和曾鹏云[12]等建立了ABH 动力学模型,分析了ABH的能量聚集特性。ABH 在工程应用方面的研究相对较少: 何璞等[13]针对机翼梁结构设计了一种ABH 盒式结构,实现了对主梁全频带的减振效果;王小东等[14]针对直升机驾驶舱复杂的噪声问题,提出基于ABH 效应的内嵌式和附加式2 种减振降噪设计方案,取得了良好的降噪效果。但以上研究的对象均为“薄板”类结构,针对水下航行器承压板这种“厚板”结构的减振设计问题尚无相关研究。针对此,文中借鉴文献[14]中提出的附加式ABH 结构设计思路,通过优化设计参数,结合承压板结构特点及工程设计要求,设计了一种减振圆板附属结构,并通过试验验证了其减振效果,可为探测声学阵列减振设计提供参考。

1 ABH 基本原理

在薄板楔形结构中,如果结构的厚度以幂函数h(x)=εxm(m≥2)形式减小,弯曲波的波速会随着厚度的减小而逐渐减小。在理想的情况下波速可减小为零,即能实现波的零反射,这种楔形结构就称为ABH 结构,如果将一维厚度幂率曲线沿中心最低点旋转一周嵌入到平板中,就形成了二维ABH 结构。

弯曲波在二维ABH 结构中传播的控制方程为[15]

式中:D(x,y)为板的弯曲刚度,D(x,y)=Eh3(x,y)/(12×(1-µ2)) ;E为弹性模量;µ为 泊松比;ρ为结构材料密度;w为挠度;ω为角频率。

式(1)的解可以写为

式中:A(x,y)为 振幅;φ (x,y)为 相位;kp为波数。将式(2)代入式(1),若使等式成立,则等式左侧的实部和虚部都必须为0。由实部为0 并舍弃关于A(x,y)和φ(x,y)的高阶导数项,可以得到

式中,k(x,y)为与位置有关的波数。

弯曲波的累积相位可以写作由楔形结构的任一点x到楔形边缘的积分

由式(3)和式(4)可以看到,当m≥2时,Φ趋于无穷大,弯曲波将无法传递到达结构边缘,也就不会发生反射,因此弯曲波能量聚集在结构边缘,即产生了ABH 效应。

2 结构设计

2.1 总体方案

承压板是将水下航行器动力系统机械振动传递到声学阵列接收端的重要部件之一。文中以某水下航行器承压板结构为基础,利用ABH 原理对声学装置承压板进行了减振设计: 在承压板后方附加ABH 减振圆板,承压板及圆板材料均为铝合金。减振圆板中间处为直径ϕ50 mm 的圆台,圆台上开有8 个直径ϕ3.2 mm 的通孔,利用8 个M3 螺钉与承压板相应螺纹孔固连,承压板模型如图1 所示,ABH 圆板模型如图2 所示,装配模型如图3 所示。

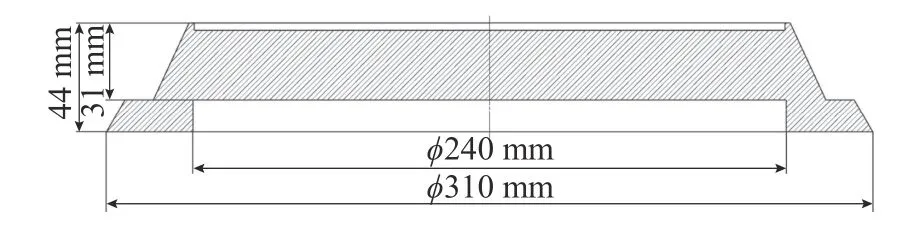
图1 承压板尺寸图Fig.1 Bearing plate size

图2 ABH 圆板尺寸图Fig.2 ABH circular plate size

图3 ABH 圆板装配模型Fig.3 Assembly model of the ABH circular plate

2.2 ABH 圆板优化设计

ABH 圆板由中间圆台向外延伸直至圆板边缘为厚度变化区域(按幂率曲线变化),理论上其最薄处为0,但在实际加工中必然存在一定厚度,即截断厚度。考虑到承压板的实际安装及使用情况,对ABH 圆板的尺寸有一定限制: 其外径不得超过ϕ200 mm,厚度不得超过7 mm。在此基础上,对ABH 圆板的结构参数进行优化设计。

考虑带有截断厚度的ABH 幂率曲线为h(x)=εxm+h(m≥2),其中h为截断厚度。

首先考察参数m取值。m为幂函数的指数且m≥2: 若m>2,则幂函数斜率陡增,即ABH 圆板的厚度增加剧烈,不能满足工程使用需要,因此设定m=2。

其次考察参数 ε取值。表1 列出了参数 ε变化时,ABH 圆板的厚度变化情况。可以看出,当ε=0.000 4 时,圆板厚度过薄,不利于机械加工且容易产生翘曲变形,同时圆板厚度不得超过7 mm,因此取ε=0.000 5～0.001 1。

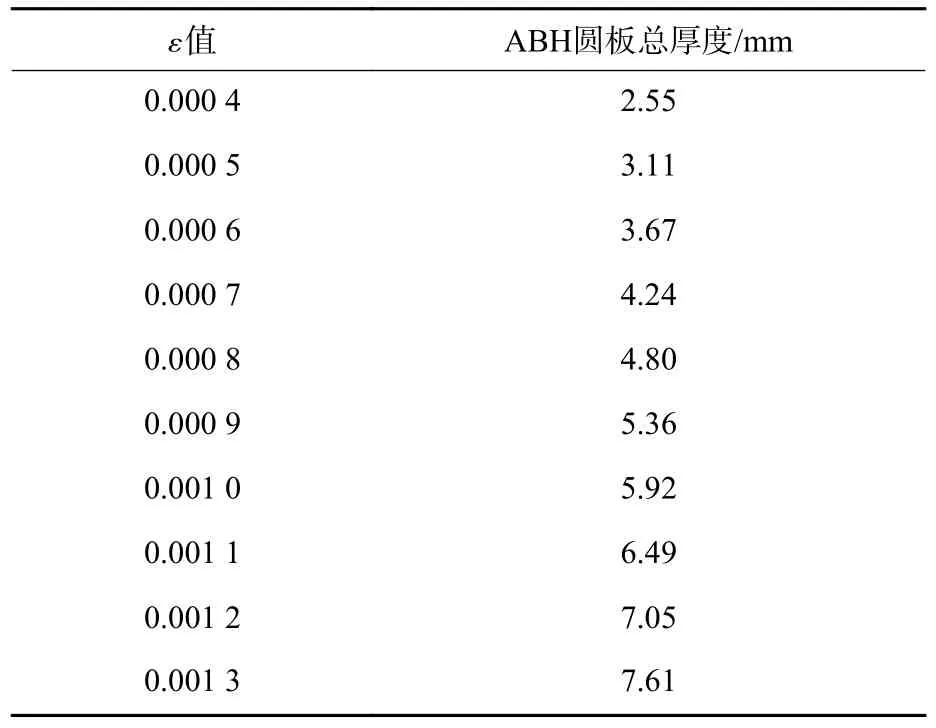
表1 ε 不同时圆板厚度Table 1 Thickness of round plate with different ε

利用有限元软件Abaqus 建立直径ϕ220 mm,厚度为5 mm 的圆板,将ABH 减振圆板安装在其上,材料全部为铝合金,连接方式与图3 一致。采用自由状态下的扫频激励(激励频段50 Hz～10 kHz)仿真分析 ε不同取值时响应点的传递损失函数曲线和总加速度级情况(设定m=2,h=0.3),激励源F位置为圆板边缘,响应点R位置为圆板中心,仿真模型如图4 所示,分析结果见图5 及表2。

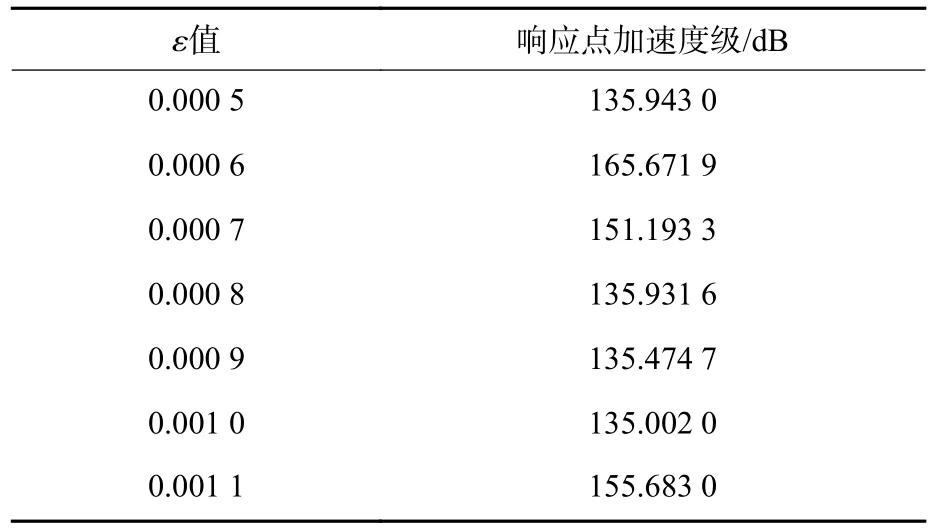
表2 不同ε 时响应点R 加速度级Table 2 Acceleration level of response point R at different ε

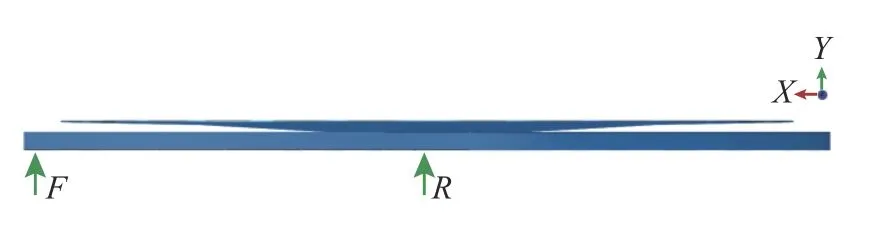
图4 ABU 圆板仿真模型Fig.4 Simulation Modal of ABH circular plate

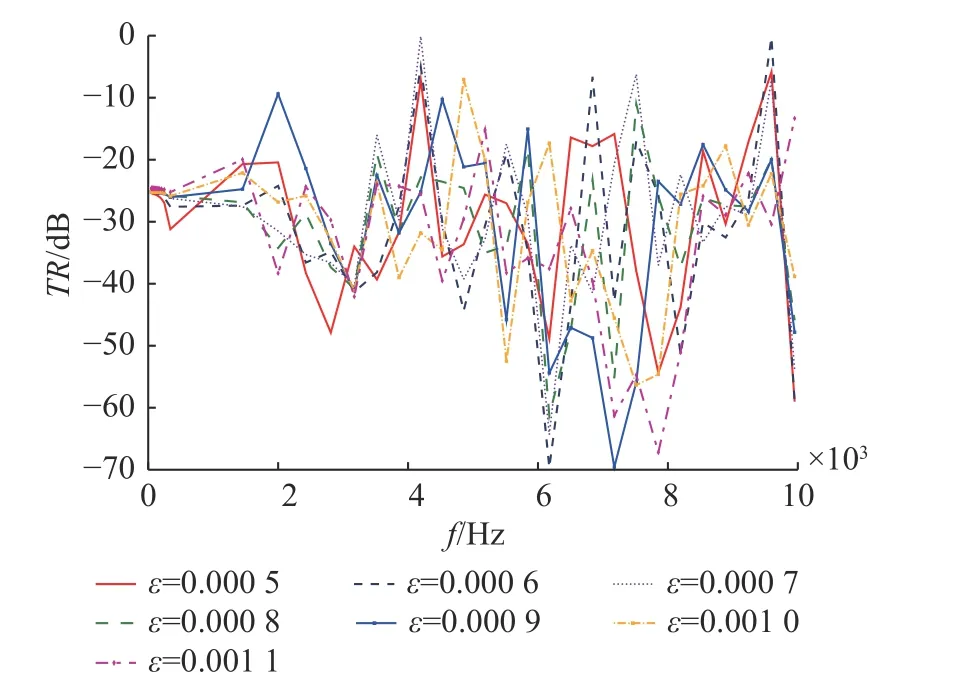
图5 不同ε 时响应点R 传递损失函数曲线Fig.5 Transfer loss function curves of response point R at different ε

传递损失函数定义

式中:TR为传递损失函数;Uout为响应点位移;Uin为激励端位移。

加速度振级计算公式为

式中:La为加速度振级;Ae为加速度有效值,计算时测试数据的均方根值;A0为加速度基准值,A0=1×10-6m/s2。

从图5 中可以看出: 当ε 变化时,响应点的传递损失函数曲线变化趋势基本一致,难以直接判断性能优劣。从表2 可以看出: 当ε=0.001 时,响应点的加速度振级最小。

最后考察参数h取值。仿真分析当h=0.1～1 mm(步长0.1 mm)时,响应点的传递损失函数曲线和加速度级变化情况(设定m=2,ε=0.001)如图6 及表3所示。

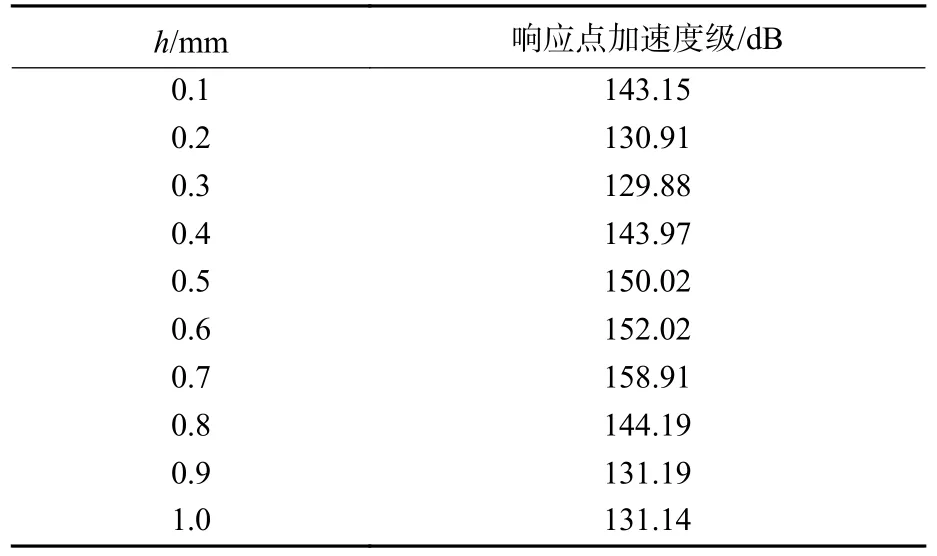
表3 不同h 时响应点R 加速度级Table 3 Acceleration level of response point R at different h

图6 不同 h 时响应点 R 传递损失函数曲线Fig.6 Transfer loss function curves of response point R at different h

从图6 中可以看出: 当h变化时,响应点的传递损失函数曲线变化趋势基本一致,难以直接判断性能优劣。从表3 中可以看出: 当h=0.3 时,响应点的加速度振级最小。

从以上分析可以确定ABH 圆板的结构控制参数为ε=0.001,m=2,h=0.3 mm,以此参数加工承压板试验样机如图7 所示。

图7 加工样机Fig.7 Prototype

3 减振性能测试

3.1 圆板减振性能测试

1) 测试方法

采用悬吊装置对样机进行固定安装,悬吊装置由固定支架和弹性绳组成,其中固定支架具有足够的刚度,能够确保被测样件的安全;弹性绳具有合理的刚度,满足试验测试的要求,减少对被测样机的影响。试验采用激振器激励,激励方向为轴向(承压板轴心方向),在激励点附近和承压板中心位置布置加速度传感器用于采集数据。试验原理如图8 所示。

图8 轴向激励试验原理图Fig.8 Principle of axial excitation test

2) 测试频带划分

测试时采用单频激励和扫频激励2 种方式: 单频激励为100 Hz～10 kHz,其中100 Hz～1 kHz 划分步长为100 Hz,1～10 kHz 划分步长为1 kHz;扫频激励划分为50～500 Hz,500 Hz～1 kHz,1～10 kHz(步长1 kHz)。

3) 数据处理方法

采集到的测试数据通过加速度振级算法得到激励端和采集端的加速度振级,二者求差得到振级落差数据,以此来评估减振效果。

振级落差计算公式为

式中:TL为振级落差;L激励端为激励端振级;L采集端为采集端振级。

4) 测试结果分析

设置2 个对比组: 第1 个是在单频激励下圆板安装1 个ABH 板,对比有无阻尼对减振性能的影响;第2 个是在扫频激励下圆板分别安装1 个ABH 减振圆板、1 个施加VHB(very high bond)阻尼的ABH 板或2 个ABH 减振圆板。试验测试数据如表4～5 及图9～10 所示,表中数值高的一方字体变粗,以便于对比减振效果。

表4 单频激励下振级落差对比Table 4 Comparison of vibration level drop under singlefrequency excitation

表5 扫频激励下振级落差对比Table 5 Comparison of vibration level drop under sweepfrequency excitation

图9 单频激励下振级落差对比曲线Fig.9 Curves of vibration level drop under singlefrequency excitation

图10 扫频激励下振级落差对比曲线Fig.10 Curves of vibration level drop under sweepfrequency excitation

从表4～5 及图9～10 可知: 在ABH 圆板边缘施加阻尼在单频激励下的某些频率点具有更优的减振效果;在扫频激励下的多数频带内其减振效果不如单层ABH 圆板。

3.2 承压板减振性能测试

1) 测试方法

测试方法同3.1 节,增加径向(垂直于承压板轴心方向)激励工况,其试验原理如图11 所示。

图11 径向激励试验原理图Fig.11 Principle of radial excitation test

2) 测试频带划分

测试时在测试设备许用量程范围内尽可能拓宽测试频带,同时考虑工程实际,将测试频带分为以下9 个范围: 首先划分3 个频带最宽的频段,即50～1 000 Hz、50～2 000 Hz 和50～10 000 Hz;其次将50～2 000 Hz 低频段细分为50～500 Hz、500～1 000 Hz、1 000～1 500 Hz 和1 500～2 000 Hz 等4 个频段;最后针对动力系统工作轴频划分100～200 Hz 和200～300 Hz 两频段。频段划分情况如图12 所示。

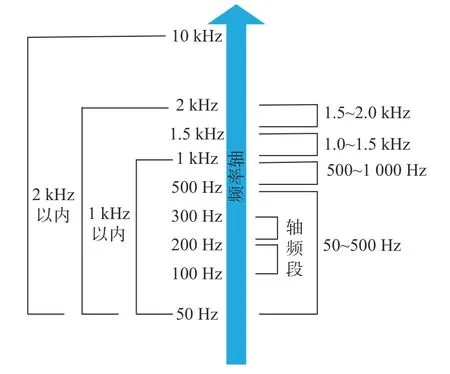
图12 承压板减振性能测试频带划分Fig.12 Frequency band division of bearing plate during vibration reduction performance test

3) 测试结果分析

设置3 种对比组: 一是承压板光板;二是承压板安装单层ABH 减振圆板;三是承压板安装双层ABH 减振圆板。振级落差对比数据如表6 所示,对轴向激励和径向激励数值对比中数值高的一方字体变粗,以便对比减振效果。响应点加速度(a)频谱曲线如图13 和图14 所示,加速度振级落差(TLa)频谱曲线如图15 和16 所示。

表6 振级落差测试结果Table 6 Test results of vibration level drop

图13 轴向激励响应点加速度频谱Fig.13 Response point acceleration spectrum under axial excitation

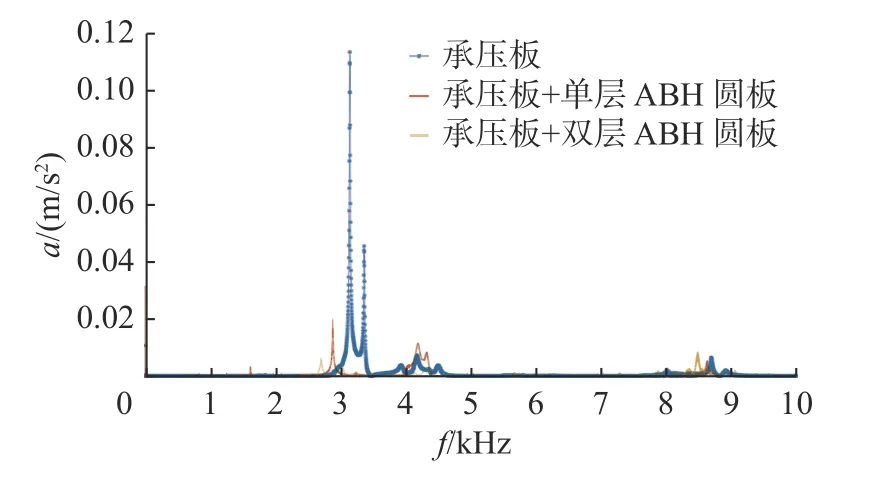
图14 径向激励响应点加速度频谱Fig.14 Response point acceleration spectrum under radial excitation

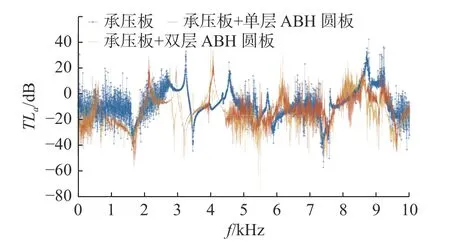
图16 径向激励响应点振级落差频谱Fig.16 Response point vibration level drop spectrum under radial excitation

a.轴向激励结果分析

通过上述图表可以看出: 在所测试的9 个频带内,带有ABH 减振圆板的承压板在低频段(2 kHz以内)和高频段(2～10 kHz)的减振性能均优于承压板光板。特别的,50 Hz～2 kHz 和50 Hz～10 kHz 频段内二者振级落差的差值分别达到5.16 dB 和7.43 dB,减振效果比较明显。含有双层ABH 减振圆板的承压板振级落差在50～500 Hz、50 Hz～10 kHz、100～200 Hz 和200～300 Hz 频段内最大,但是数值差距并不大,某些频带内甚至还有低于承压板光板的数据。综合来看,单层ABH 减振圆板的减振性能突出,双层ABH 减振圆板对减振性能的提升效果不明显。

b.径向激励结果分析

通过图表数据可以看出: 带有ABH 减振圆板的承压板在50～500 Hz、500 Hz～1 kHz、1～1.5 kHz、1.5～2 kHz、50 Hz～1 kHz、50 Hz～2 kHz 和50 Hz～10 kHz 频段内二者振级落差的差值分别达到7.02、7.95、5.24、13.56、11.91、15.07 和8.22 dB,减振效果明显。含有双层ABH 减振圆板的承压板振级落差在50 Hz～10 kHz、100～200 Hz 和200～300 Hz频段内最大。综合来看,单层ABH 减振圆板的减振性能突出,双层ABH 减振圆板对减振性能的提升效果不明显。

综上所述,所设计的基于ABH 原理的减振圆板不仅在低频段有良好的减振效果,在高频段同样有良好的减振效果。同时,试验时用的承压板质量为5 185.3 g,ABH 减振圆板质量为159.6 g,减振圆板质量为承压板重量的3%。因此ABH 减振圆板实现了宽频、轻质及高效的减振功能,具有较高的工程实用价值。

4 结束语

文中针对水下航行器探测声学阵列承压板结构设计了一种基于ABH 原理的减振圆板附属结构,并测试了其减振性能,详细说明了测试方法、激励频段设置、数据采集及处理方法,并对试验结果进行了分析。结果表明,所设计的ABH 减振圆板在低频段和高频段均具有良好的减振效果。下一步将针对实际边界条件下的减振性能进行深入研究。