非线性支承下磁悬浮转子系统μ综合控制的研究

葛萍萍，王念先

（1.武汉科技大学 机械自动化学院，武汉 430081；2.冶金装备及其控制教育部重点实验室，武汉 430081）

磁悬浮轴承是利用可控电磁力将转子稳定悬浮的一种支承装置，与传统轴承相比，具有无接触、无磨损、无需润滑、精度高，刚度和阻尼可调等优点，广泛应用于航空航天、超高速精密加工和机器人等领域［1］。当磁悬浮转子系统的工况复杂时，磁性材料的相对磁导率变化明显，磁悬浮轴承非线性支承特性明显增加，转子不平衡力和负载对系统影响的复杂性增加，因此磁悬浮转子系统需要性能良好的控制器对其进行控制。

由于漏磁、磁饱和的影响，磁悬浮轴承的支承特性表现出明显的非线性：文献［2］基于动态磁路模型，针对磁悬浮轴承中漏磁、磁饱和的影响，提出多目标优化方法并用试验证明其有效性；文献［3］采用新的建模方法精确计算出边缘通量和泄漏系数，并用试验证明此建模方法的准确性较高；文献［4］提出一种非线性磁路方法，建立磁悬浮轴承的承载力解析模型，考虑了边缘磁通、漏磁通、磁饱和，因此该模型精度较高；文献［5-6］发现考虑漏磁、磁饱和等引起的支承非线性后，转子不平衡响应中包含大量的超谐波信号，转子响应更加复杂。

关于非线性转子系统的振动抑制问题，已有许多学者开展了研究：文献［7］采用神经网络PID的电磁执行器实现了裂纹转子系统非线性振动的主动控制；文献［8］考虑了陀螺效应和非线性磁悬浮支承力，采用精确非线性反馈实现了磁悬浮转子系统的有效控制；文献［9］采用时变刚度比例-微分（PD）控制器抑制了磁悬浮轴承支承刚性转子的非线性振动；文献［10］针对开关功率放大器的非线性现象，采用自适应比例控制，避免了非线性现象；文献［11］采用μ综合鲁棒控制使磁悬浮单转子试验台平稳通过一阶临界转速，避免了磁悬浮轴承的电流饱和。

为抑制磁悬浮轴承支承力非线性的影响，本文选取μ综合控制器对非线性支承下含不平衡故障的磁悬浮转子系统进行控制，并针对μ综合控制下系统的磁饱和、漏磁非线性问题，在频域上进行系统不平衡响应的基频和倍频幅值研究。

1 非线性支承磁悬浮转子系统模型

1.1 磁悬浮转子系统结构

磁悬浮转子系统结构如图1所示，转子系统由转轴与圆盘构成，转轴为空心结构，外径为25 mm，内径为15 mm。转子长度为580 mm，从左到右离散为28个单元，共29个节点，磁悬浮轴承支承点位于1#和29#节点，圆盘位于25#节点，离散后的转子单元长度小于单元直径［12］。基于转子的质量和不平衡力，本文采用八磁极结构径向磁悬浮轴承，其主要参数见表1。

表1 径向磁悬浮轴承主要参数Tab.1 Main parameters of radial magnetic bearing

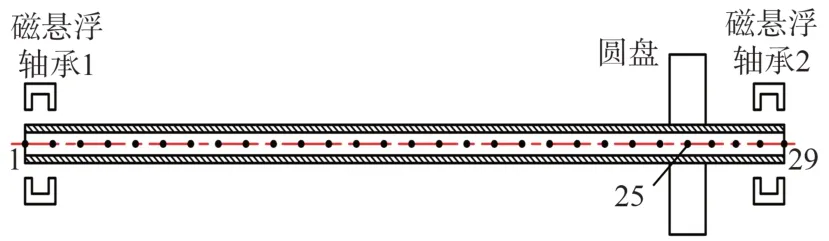
图1 磁悬浮转子系统结构简图Fig.1 Structure diagram of magnetic levitation rotor system

为分析方便，进行以下3 种假设：1）视转子的轴向自由度和径向自由度完全解耦，只分析转子的径向自由度；2）忽略转子和圆盘自身重力对系统的影响；3）圆盘为刚性体，可用集中质量单元块表示。

1.2 非线性支承力模型

采用差动控制的八磁极径向磁悬浮轴承结构，控制原理如图2 所示：x为转子位置，g0为转子气隙长度，Ix为转子系统控制电流，Ib为转子系统偏置电流。

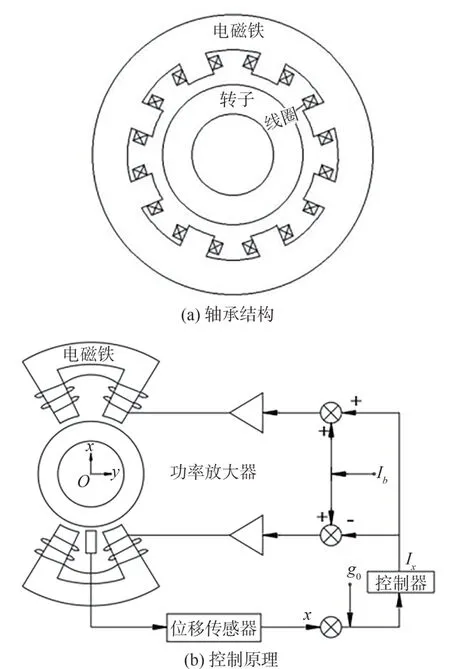
图2 八磁极径向磁悬浮轴承结构及控制原理图Fig.2 Structure and control principle diagram of eight pole radial magnetic bearing

忽略铁磁材料磁滞、涡流和磁场耦合的影响，考虑磁饱和、漏磁建立磁悬浮轴承支承力Fa模型［4］，即

式中：α为磁极对夹角的一半；μ0为真空磁导率；Ap为磁极面积；Φ1，Φ3分别为通过磁路气隙中的磁通；N为线圈匝数；Rg1，Rg2，Rg3，Rg4分别为一个磁极对处左上、右上、左下、右下气隙的磁阻；Rr为转子磁阻；Rk为漏磁磁路模型磁阻；Ry为磁轭磁阻；Rp为磁饱和影响下磁极磁阻。

先计算各磁阻（包含Rg，Rk，Rp，Ry和Rr），再对等效磁路进行分析得到磁通，并由磁通进一步计算出转子系统中磁悬浮轴承的支承力，如图3 所示。线性支承力忽略了系统的漏磁、磁饱和效应，而非线性支承力考虑了系统的漏磁、磁饱和效应。

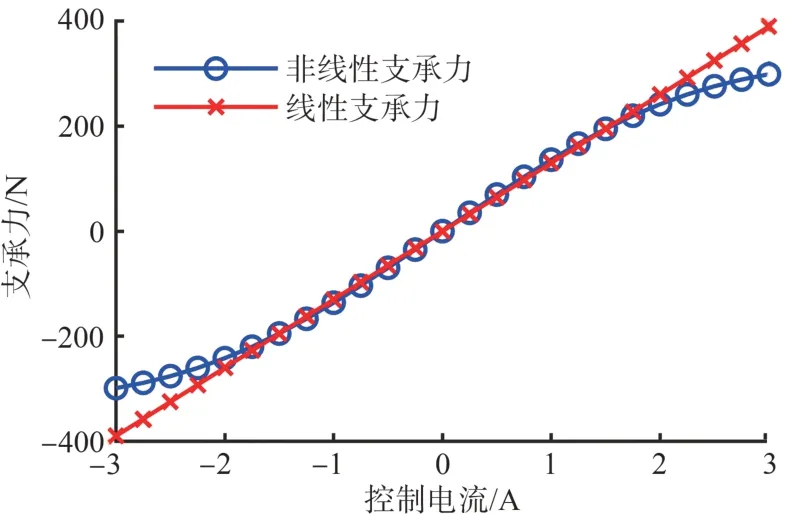
图3 磁悬浮轴承支承力与控制电流关系Fig.3 Relationship between supporting force of magnetic bearing and control current

1.3 磁悬浮转子系统控制模型

采用有限元法对磁悬浮转子系统进行建模，物理坐标下的转子系统动力学方程为

式中：M，D，Ω，J，K分别为磁悬浮转子系统的质量矩阵、阻尼矩阵、转动矩阵、陀螺矩阵、刚度矩阵，J为斜对称矩阵，M，D，Ω，K矩阵是对称且正定的；q为转子位移矢量；B1为非线性支承力分配系数矩阵；B2为系统所受干扰力系数矩阵；Fmag为转子系统非线性支承力；f为系统所受干扰力（主要为不平衡力和负载）；C为传感器轴向分布矩阵；xi，θyi分别为i#节点处x方向的平动和绕y轴的转动；yi，θxi分别为i#节点处y方向的平动和绕x轴的转动。

在i=0，y=0（平衡点）处对（1）式的Fa进行线性化，得到线性化后的Fmag，即

式中：ki为电流刚度，130 N/A；i为控制电流；kx1为位移刚度，2.5×105N/m；x1为控制位移。

由于磁悬浮转子系统的全阶模型状态量过多，难以直接用于控制器的设计，并且转子运行过程中高阶振型很难被激发出来，因此本文采用模态分析法与模态截断法保留转子前2 阶的刚性模态和柔性模态。

将系统状态空间方程转换到模态坐标下，不考虑系统干扰力f的影响，系统的坐标转换为

式中：Φ为模态变换矩阵的前4 阶；η为模态坐标矢量。

模态坐标下的磁悬浮转子系统动力学方程（转子为细长轴且转速较低，故忽略转子陀螺效应）为

式中：Mr，Kr分别为系统模态截断后的质量矩阵、刚度矩阵；y为输出位移。

截断后系统的η有8 个状态变量，由前2 阶的刚性模态和弯曲模态组成。截断后系统模型可表示为状态空间方程形式，即

式中：Ar，Br，Cr，xr，yr分别为系统截断后的状态矩阵、输入矩阵、输出矩阵、状态向量、输出位移；u为输入系统的控制电流。

1.4 功率放大器与位移传感器建模

功率放大器是闭环系统的关键部件，接收控制电压，为磁悬浮轴承线圈产生足够电流。采用系统辨识的方法，对功率放大器进行扫频试验得到频响特性曲线，再通过拟合曲线得到功率放大器的传递函数为

式中：s为一个复数变量，表示系统的频率响应。

将Ga(s)转为状态空间方程，即

式中：Aa，Ba，Ca，xa分别为功率放大器的状态矩阵、输入矩阵、输出矩阵、状态向量；ua为功率放大器输入电压；ya为功率放大器输出电流。

本文采用电涡流位移传感器测量转子径向运动。根据文献［11］的频率响应曲线，位移传感器的传递函数为

将Gs(s)转换为状态空间方程，即

式中：As，Bs，Cs，xs分别为传感器的状态矩阵、输入矩阵、输出矩阵、状态向量；us为传感器输入转子实际位置；ys为传感器输出电流。

2 闭环系统控制器的设计

2.1 系统权函数选取和系统不确定性

将功率放大器、磁悬浮转子系统与位移传感器相连，得到闭环系统控制模型Gsys，Gsys为四输入与四输出结构。基于四块结构设计μ综合控制器，选取目标函数为

式中：We为输入指标权函数；Wr为参考输入权函数；Wd为输入扰动权函数；Wu为作动器控制输入权函数；So，Ti，KSo，GsysSi分别为系统混合灵敏度函数、补灵敏度函数、控制灵敏度函数、动态灵敏度函数。

磁悬浮转子增广系统框图如图4 所示，K为系统的μ综合控制器，P为磁悬浮转子增广系统，d为系统输入扰动，本文为不平衡力和负载；r为系统参考输入，本文设置参考输入电压为0；u为系统控制输入，本文为控制器输出电压；e为系统跟踪误差，本文为参考输入电压与位移误差电压的差值；y为系统位移输出；ze，zu为性能加权输出；Δm为系统的频率参数摄动，Δm={diag(δ1，δ2)；δn∈R}，具有对角结构。本文取一阶弯曲模态频率的摄动范围δ1为- 5%～5%，二阶弯曲模态频率的摄动范围δ2为-2%～2%。

图4 增广μ综合控制系统框图Fig.4 Block diagram of augmented μ-synthesis control system

不确定状态空间An为

式中：fn为n阶弯曲模态频率；ξn为模态阻尼比；σn为n阶弯曲模态频率不确定性。

图4虚线框中的P为

（14）式中多输入多输出系统的权函数通常选取对角矩阵形式，即

根据ISO 14893-3：2006“Mechanical vibration—Vibration of rotating machinery equipped with active magnetic bearings—Part 3：Evaluation of stability margin”选择系统灵敏度函数的奇异值范围，进而得出wr的合理范围为0.2 ～ 1.0。

（15）式中的we为一阶低通滤波器形式，即

式中：e为一阶低通滤波器增益；A为积分常数，代表低频刚度要求；fe为穿越频率。

系统加性不确定性由wu表示，wu为二阶高通滤波器形式，即

式中：a为增益，为了防止电压饱和，应取较小常数；ζ通常为最佳阻尼比，取0.707；为不激发系统高频模态，使控制器的增益在高频处滚降，应添加滚降频率f1和高频极点频率f2。

（15）式中的wd为

式中：b为加权系数；ad为系统干扰的最大幅值，大于干扰信号的频率。

基于权函数的选取经验，并经过调试和对系统灵敏度函数与结构奇异值μ的分析，确定权函数为

2.2 闭环系统μ综合分析

μ综合分析框架如图5 所示：将磁悬浮转子增广系统P与控制器K（s）通过下线性分式变换得到M，即

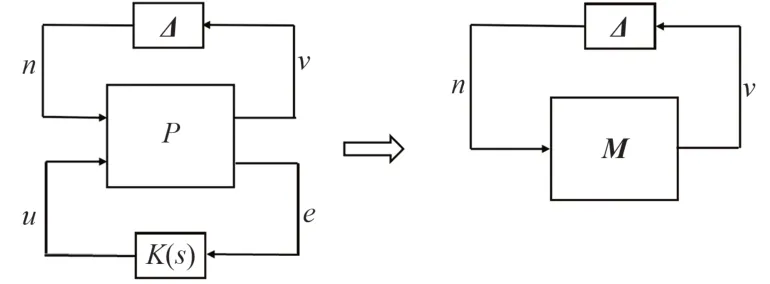
图5 μ综合分析框架图Fig.5 Framework diagram of μ-synthesis analysis

图5中的不确定性用Δ表示，Δ={diag(Δm，Δp)；Δm∈C2×2，Δp∈C4×4}。

系统结构奇异值μ（M）定义为

式中：min(Δ) 为使det(I-MΔ) = 0（即I-MΔ为奇异的）时的最小(Δ)。若无Δ∈Δ*，使I-MΔ为奇异的，则μΔ*(M) = 0。系统的稳定性和鲁棒性可以通过求解矩阵M的结构奇异值μ判定。

对于结构不确定性系统，为保证系统稳定性须满足μΔ[M11(s)]＜1。系统鲁棒性的充要条件为μΔ*[M(s)]＜1。

3 仿真分析

3.1 闭环转子系统仿真模型

忽略磁悬浮转子陀螺效应，四输入和四输出转子模型Gsys在2 个竖直平面解耦为2 个完全相同的二输入二输出转子系统。下文仅展示其中一个平面中转子系统输入输出状态。在Simulink仿真环境下，将μ综合控制器与磁悬浮转子系统相连得到闭环系统仿真模型，如图6 所示，ur为系统参考输入电压信号，x为系统不平衡响应位移输出。PID 控制器的3 个参数分别为：KP=40，KI=100，KD=0.05。综合控制器为状态空间方程形式，即

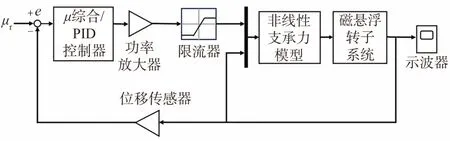
图6 闭环转子系统仿真框图Fig.6 Block diagram of closed-loop rotor system simulation

式中：ue为输入误差电压，ye为输出控制电压。

3.2 闭环转子系统稳定性和鲁棒性分析

根据给定的结构不确定性转子系统与四组加权函数相连，得到不确定性系统增广矩阵。使用μ综合鲁棒控制工具箱中的dksyn进行迭代计算，得到系统的μ综合控制器。闭环转子系统的稳定性和鲁棒性如图7 所示：μΔm(M11)的最大值为0.043 7＜1，μΔ(M)的最大值0.61＜1，因此，μ综合控制器可使闭环系统满足稳定性和鲁棒性的要求。

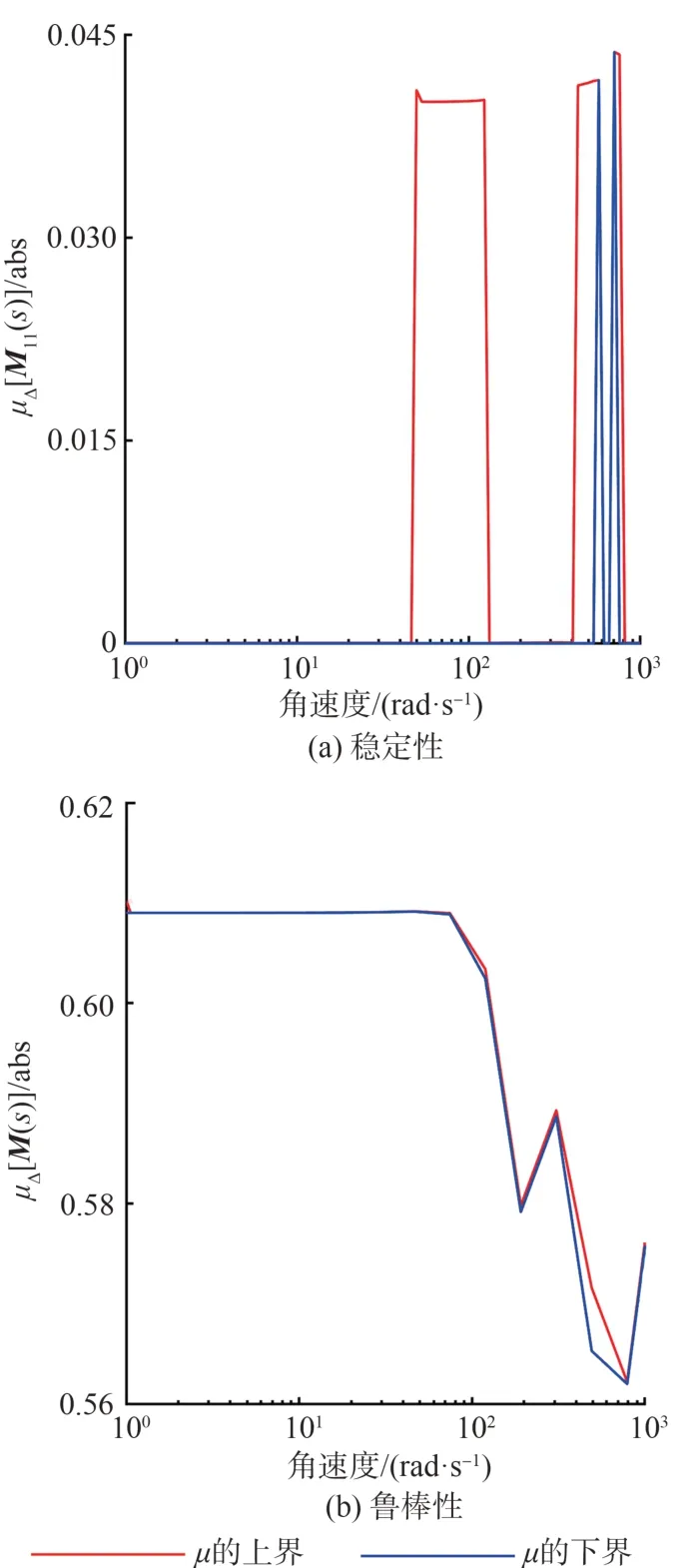
图7 闭环转子系统的稳定性和鲁棒性Fig.7 Stability and robustness of closed-loop rotor system

3.3 闭环转子系统起浮性能和抗干扰性能分析

为模拟转子系统的起浮，本文在参考输入电压ur处输入阶跃信号。转子29#节点x方向的阶跃响应如图8所示：转子在0.03 s处从保护轴承上快速起浮，振幅在0.15 s 处完全衰减，并且存在24.46%的超调量。转子起浮速度比衰减速度快，超调量小，避免了转子在起浮期间与保护轴承的接触，闭环转子系统的起浮性能良好。

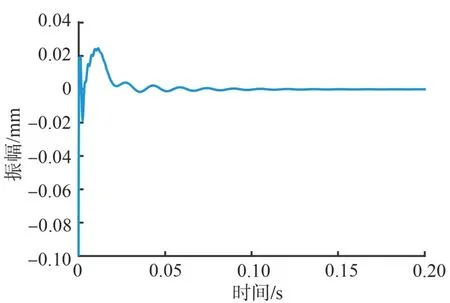
图8 闭环转子系统阶跃响应Fig.8 Step response of closed-loop rotor system

转子29#节点x方向的扰动响应如图9 所示：在0.2 s 处对圆盘施加100 N 干扰力后，转子在0.37 s 重新回到平衡位置0 处并维持在此处。转子重回平衡位置的速度快且可以重新维持稳定运行状态，闭环转子系统抗干扰性能良好。

图9 闭环转子系统扰动响应Fig.9 Disturbance response of closed-loop rotor system

3.4 闭环转子系统不平衡响应分析

为研究闭环转子系统在不同角速度下的不平衡响应控制效果：参考输入电压ur=0；外负载FL=0；25#节点处的不平衡量为2.1×10-4kg · m。在不同角速度下，转子29#节点处x方向的不平衡响应如图10 所示：与PID 控制相比，在给定角速度范围内，μ综合控制下系统的基频fi振幅显著减小；当角速度ω为200 ～ 360 rad/s 时，μ综合控制下的系统不平衡响应振幅与PID 控制下相比显著降低；由于支承非线性的影响，PID控制下的系统响应出现了倍频3fi，而μ综合控制实现了对3fi振幅的显著抑制。在给定的角速度条件下，与PID 控制相比，μ综合控制较好地抑制了非线性对系统的影响。

图10 不同角速度下闭环转子系统不平衡响应频域图Fig.10 Frequency domain diagram of unbalanced response of closed-loop rotor system under different angular velocitys

为研究闭环转子系统在不同负载下不平衡响应的控制效果：参考输入电压ur=0，转子角速度ω=280 rad/s，25#节点处的不平衡量为2.1×10-4kg · m。在圆盘竖直方向施加不同的负载FL，转子29#节点处x方向的不平衡响应如图11 所示：在给定负载范围内，μ综合控制下系统的基频fi振幅明显小于PID 控制；PID 控制下系统的不平衡响应中除其基频fi外，还有倍频（2fi和3fi）被激发出来，而μ综合控制下系统的倍频振幅被明显抑制。说明支承非线性对系统的影响被削弱，且在给定负载范围内，当FL为20 ～ 160 N 时，μ综合控制下的系统不平衡响应振幅相比PID控制下显著降低。

4 结论

考虑磁饱和、漏磁效应建立了非线性支承下的磁悬浮转子系统模型。基于磁悬浮转子系统的参数不确定性和高阶未建模动态，设计了针对非线性支承下磁悬浮转子系统的μ综合控制器。得到以下结论：

1）μ综合控制能实现转子的稳定悬浮，且闭环磁悬浮转子系统具有良好的起浮性能和抗干扰性能。

2）在角速度及负载给定的范围内，与PID 控制相比，μ综合控制能有效减小不平衡响应基频fi和倍频（2fi和3fi）幅值，抑制系统的不平衡扰动和非线性效应。