基于Python聚类分析的聚类数确定方法对比

董芷欣

(格拉斯哥大学, 计算机学院, 格拉斯哥 G128QQ, 英国)

0 引言

机器学习算法为大数据处理在学术界和产业界的广泛使用给予了强大的推动力[1]。在自然语言处理和计算机视觉领域,无监督学习算法应用十分广泛,而无监督学习中适用范围最广的学习任务是聚类。聚类算法的过程旨在实现“类内的相似性和类间的排他性”的目标[2-4]。“簇”的划分是聚类算法实现的核心问题,而聚类簇个数的确定是“簇”的划分的必要条件之一[5-6]。本文根据不同聚类算法的实现过程,将聚类簇个数的划分方式归纳为显式指定和超参数推断2种方法。前者的应用算法为k-means和高斯混合聚类;后者则由层次聚类算法和Louvain算法实现。研究聚类簇个数的划分方式有助于编程者对不同聚类算法的实现,如有效性指标的选择、模型参数的调整、聚类算法的优化等。为更好地论述和比较2种划分方式的实现过程,本文选取数字切片数据进行案例研究,代码使用Jupyter notebook实现。对于不同聚类算法的结果计算Silhouette score判断不同模型的拟合优度、V-measure判断聚类结果与原类别之间的契合度。

1 聚类数确定方法

1.1 显式指定法

k-means算法是最常用的聚类算法,算法随机初始化k个聚类中心点,并计算数据中每个点到k个中心点的距离。将每个数据点与距离最近的中心点关联并聚成一类,利用均值等方法更新该类的中心值并迭代计算直到得到满意结果。高斯混合模型(GMM)也是一种常见的聚类算法,与K均值算法类似,同样使用迭代计算。高斯混合模型假设每个簇的数据都是符合高斯分布的,当前数据呈现的分布就是各个簇的高斯分布叠加在一起的结果。这2种方法运算简单、速度快,但聚类簇个数K值的确定对结果影响巨大。

在实现k-means和GMM聚类算法时,需要通过一些方法来确定聚类簇个数以便在进行聚类运算时显式地指定簇个数。本文分别采用肘部运算法则和网格搜索法获取类簇中心个数。肘部法则通过寻找损失值下降平稳的拐点来确定簇个数。以k-means为例,其以最小化样本与类簇中心的平方误差作为目标函数。畸变程度与簇内成员紧密程度呈负相关,畸变程度随类别增加而降低,在达到临界点后缓慢下降。临界点作为聚类性能较好的点被选作为聚类算法实现时显式指定的聚类个数。GMM聚类算法使用网格搜索法获取类簇中心个数,网格搜索法在部分或全部训练集上对多种参数组合进行交叉验证,以得到每个参数组合的模型训练效果,从而选出规定范围内最优参数。

1.2 超参数推断法

本文采用层次聚类算法和Louvain算法实现超参数推断。层次聚类是一种常用的聚类算法,一般采用由下向上一层一层进行聚类。算法初始将样本集中所有样本点都作为一个独立的类簇,然后依据某种准则(例如距离)合并这些初始的类簇,直到达到聚类数目或者达到事先设定条件。Louvain算法是一种基于图形的社区检测方法(community detection),每个数据点表示为1个节点,用一条边表示2个数据点之间的相似性。算法首先将节点分配给不同的簇中,这些簇在社区内部具有紧密的联系称为模块化,然后对簇进行重复测试直到模块化不再变化。

2 聚类有效性评估

由不同的数据结构决定的聚类方法并不会适用于各种数据模型,因此对聚类结果的有效性评估是非常重要的[7]。本文选取轮廓系数和V-measure作为衡量指标对聚类算法进行评估。

2.1 轮廓系数(silhouette score)

聚类结果的评价可转化为对于簇内和簇间相似度的衡量。簇的凝聚性(cohesion)度量簇内样本密切程度,而分离性(separation)度量簇间相异程度[8]。较小的簇内凝聚度和较大的簇间分离度可以使聚类结果更加理想化。轮廓系数便是类的密集与分散程度的评价指标。由样本个体的轮廓系数可推导出数据集某次聚类的轮廓系数sk:

(1)

其中,ai为样本于其同簇中其他样本的平均距离,bi为样本与其他簇中所有样本的平均距离的最小值,n为数据集中样本个数,k为聚类数。

本文中使用轮廓系数可以直观地比较出不同聚类算法对原数据集的聚类效果。

2.2 V-measure

除了使用轮廓系数对聚类效果进行内部评估外,本文还选择了一种基于外部熵的评价方法V-measure对聚类性能进行外部评估。V-measure可以准确地结合和评估聚类的两个理想方面,即同质性(homogeneity)和完整性(completeness)。同质性度量或完整性度量越大,2个类别划分越接近。V-measure反映了聚类解决方法在将特定类别的所有数据点纳入特定聚类中的成功程度,只对集群的质量进行评估[9]。本文使用该方法对比原类别与聚类所得的类别之间的相似程度。

3 案例研究

本文选用组织切片图像数据集进行案例研究,此数据集包含5000张切片图像(244×244×3),按组织种类可被分为9类:脂肪(ADI)、背景(BACK)、碎屑(DEB)、淋巴细胞(LYM)、黏液(MUC)、肌肉(MUS)、正常黏膜(NORM)、病间质(STR)和病上皮(TUM)。每种组织图像的样本数如表1所示。接着经过InceptionV3分类器的训练,将原始数据转换为5000组2048维向量,准确率为77.9%。最后采用UMAP降维方法继续将维度降为100,得到5000组100维向量作为最终研究数据集。该数据集的结构分布如图1所示。聚类算法包括K均值、GMM、层次聚类(AHC)和Louvain算法,通过计算silhouette score和V-measure评分来评估和比较效果。

图1 降维后的数据集的结构分布图

表1 组织图像种类及对应样本数

3.1 运算过程

依托于Jupyter notebook平台,使用Python代码编程实现基于2种聚类簇个数确定方法的4种聚类模型选择。聚类算法编程的总体思路为在给定的聚类簇个数区间内选择合适的效果评估方法得到最优簇个数值,使用机器学习库中的算法包对数据集进行聚类得出最终每一类中的成员数,最后计算silhouette score和V-measure比较拟合优度和类别契合度。另外,实验过程中对Scikit-learn库中使用的算法包中除聚类簇个数外其他参数进行控制变量。软件流程如图2所示。

图2 软件流程图

3.2 显式指定簇个数

k-means算法和高斯混合模型都是在实现过程中需要显式指定簇个数的聚类模型。 在使用Python的Scikit-learn机器学习库中的算法模型进行聚类学习时,因所使用数据集的真实类别数为9,故在筛选k-means()的参数n_clusters和GaussianMixture()的参数n_components时,取值均从[1,10]范围中选择。

对k-means算法前期使用肘部法则筛选最优参数n_clusters,从图3可以明显地看出,变量k在4之后减小的幅度明显变缓,因此选择最优参数4作为本实验中k-means模型的聚类簇个数,显示指定参数n_clusters = 4。为固定构建的模型,设置随机种子random_state=0, 其他参数均为默认值,结果如表2所示。

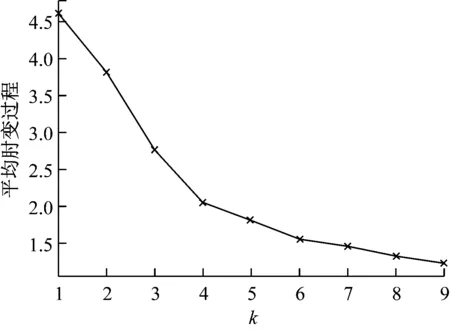
图3 肘部法则确定k值

表2 k-means模型聚类结果

在使用高斯混合模型进行聚类时,前期使用网格搜索GridSearchCV()在[1, 10]范围内得到GaussianMixture()中的参数n_components的最优值为6,因此确定6为本实验中高斯混合模型的聚类簇个数。另外,在GaussianMixture()中设参数covariance_type=’shperical’,意味着每个分量有各自的简单协方差矩阵; random_state=0, 其余参数均为默认值。高斯混合模型的聚类结果如表3所示。

表3 高斯混合模型聚类结果

3.3 超参数推断簇个数

Louvain算法和层次聚类法可以通过对超参数的设置实现聚类。本文分别对Louvain算法的解析度参数(决定社区规模)以及AgglomerativeClustering算法的距离阈值参数进行调参。通过对参数范围内不同取值所得轮廓系数及V-measure数值比较,综合2种评估指标调整参数。

Scikit-learn中,Louvain()的解析度参数resolution可以灵活地控制社区划分数量及规模[10]。 由图4可知, resolution取值为0.9时,silhouette score最高且V-measure相对较高。因此,本文选择0.9作为Louvain算法的解析度,设置超参数resolution =0.9,其余参数均为默认值,聚类结果如表4所示。

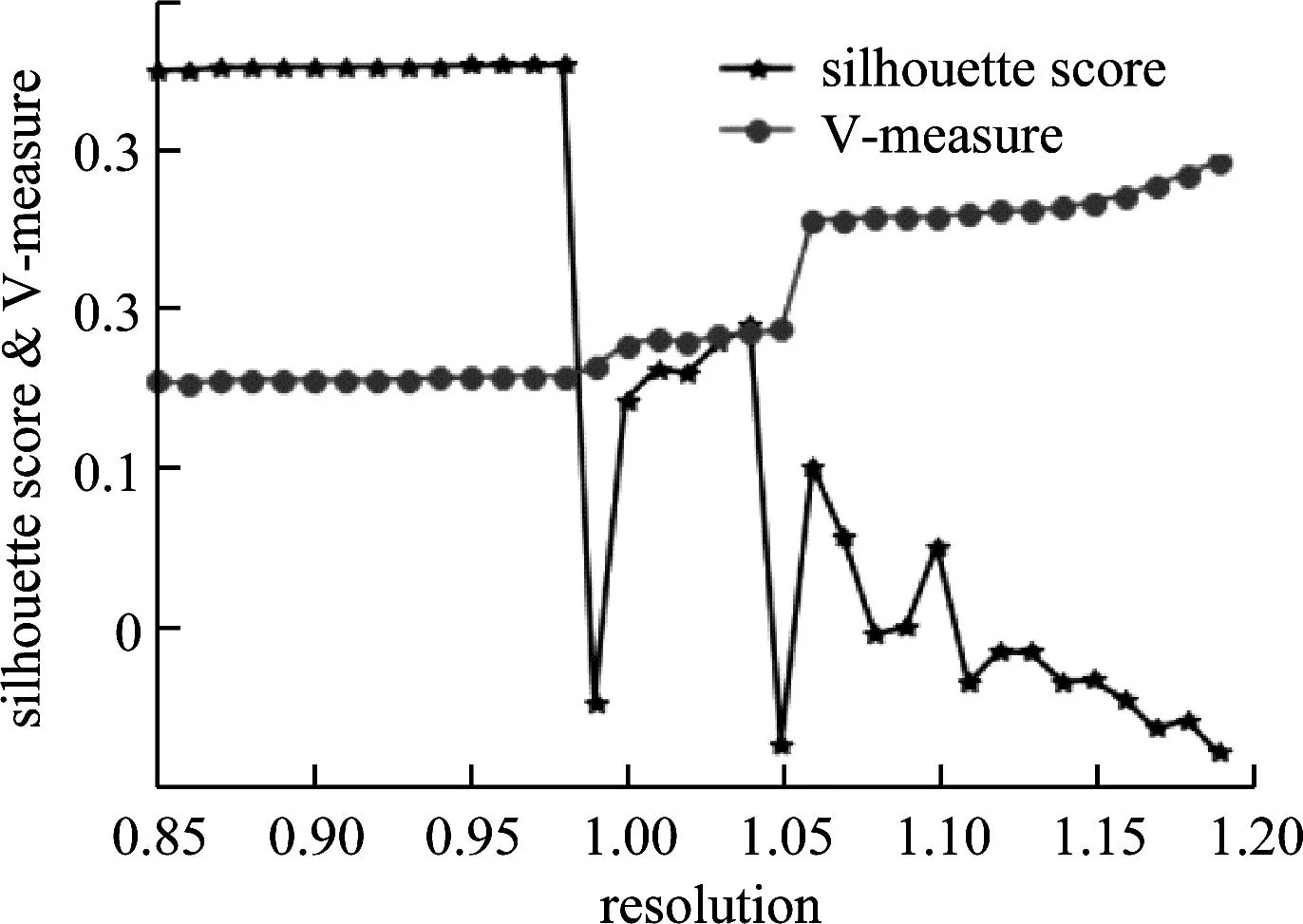
图4 Louvain算法解析度曲线

表4 Louvain模型聚类结果

层次聚类算法中,在范围1～10内对超参数distance_threshold调整,得到的轮廓系数和V-measure图像如图5所示,综合比较后选取4为参数值。用Scikit-learn库中AgglomerativeClustering()做最优层次聚类模型预测,超参数distance_threshold=4。 另外,通过比较不同linkage所得的silhouette score,如图6所示,选择average作为linkage的值,其余参数均为默认值。表5列出了层次聚类结果。

图5 层次聚类算法silhouette score和V-measure曲线

图6 AHC linkage参数比较曲线图

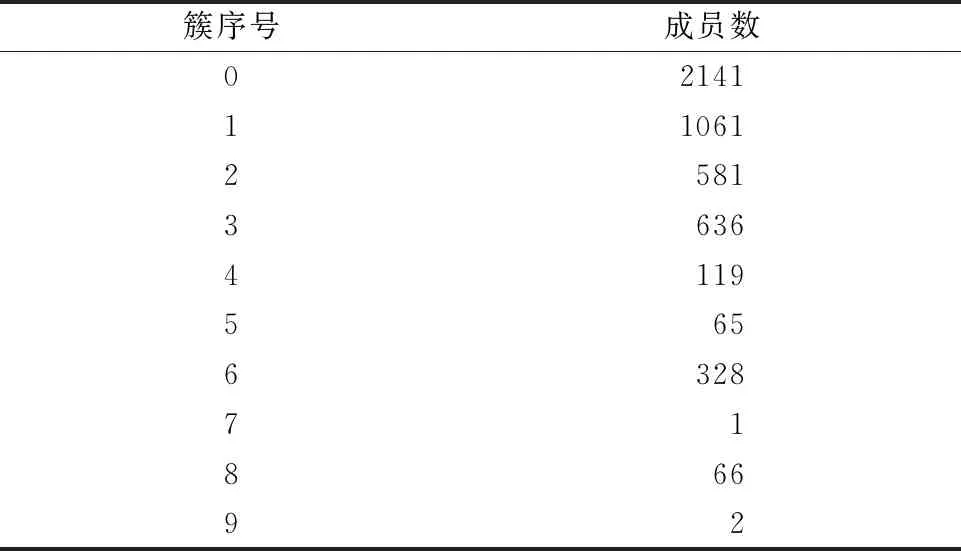
表5 层次聚类模型聚类结果

3.4 结果比较分析

通过比较4类算法的分类结果(见表6)发现,高斯混合模型和层级聚类模型对于silhouette score和V-measure的表现结果较好(均>0.4),而k-means算法和Louvain算法虽然在聚类效果上表现较好,但与原类别的相似程度相差较大。对于显式指定法中簇个数的确定方法,网格搜索结果优于肘部法则。

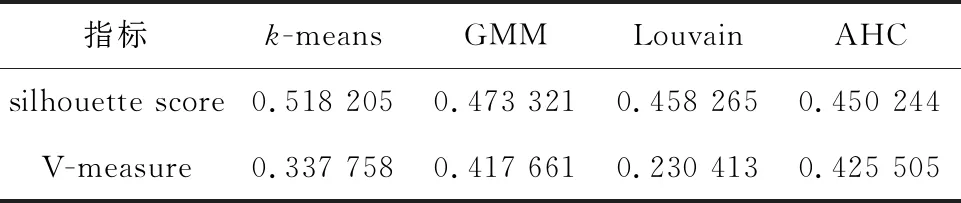
表6 分类结果比较

由图7可知,4类算法均可对BACK类实现较完整地分离。另外,ADI类在k-means、GMM和AHC算法中可以被较完整分离。分离出聚类数最多的算法是GMM,可将ADI、LYM和BACK 3类分离。从数据角度分析,LYM和DEB类别易混淆,在4类算法中聚类效果较差的类别是TUM、STR、Norm和MUC。

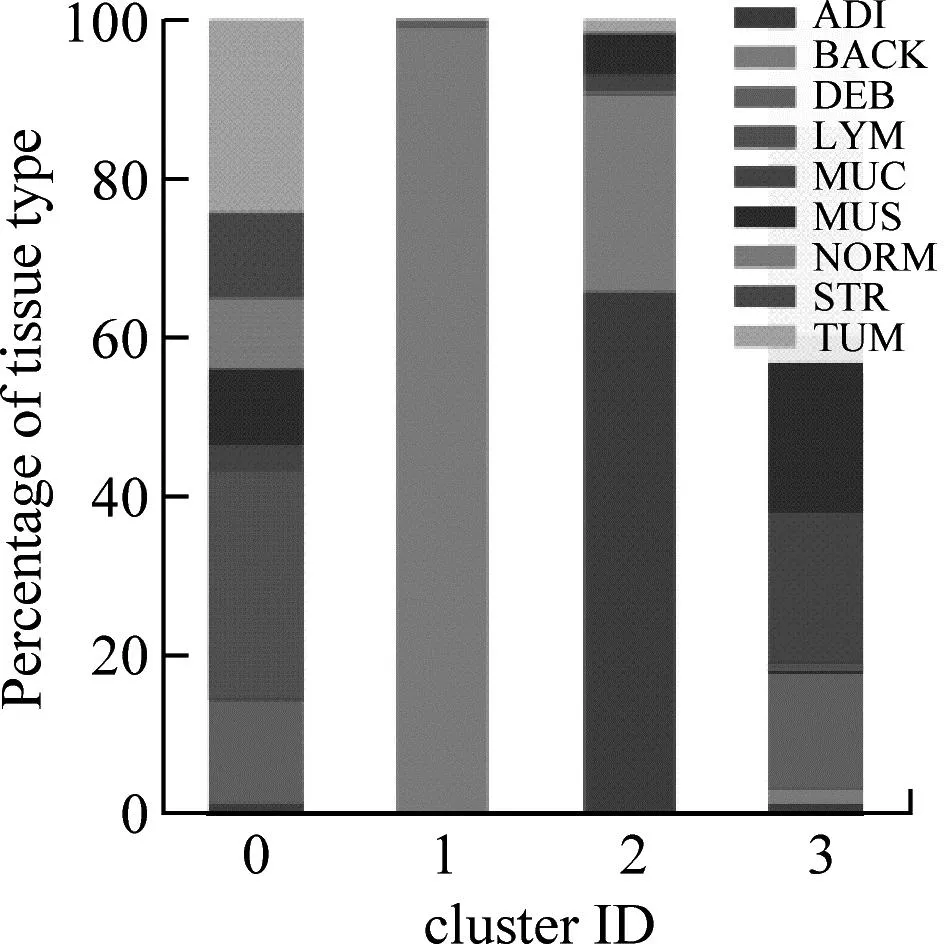
图7 4种算法的组织分类柱状图

4 总结

在确定聚类簇个数的方法中,肘部法则对于拐点的确定较为模糊,对于最终簇个数的确定可能存在争议。由聚类结果柱状图可分析,原始数据可能存在类别不平衡问题,未来可使用downsampling或upsampling方法优化原始数据。在超参数决定簇个数的代码实现中,本文只针对Louvain算法中的resolution参数以及AHC算法中的distance_threshold和linkage参数进行调整,其他参数均使用默认值或统一值,未来可从其他参数上做出调整以提高算法效率和结果表现。另外,k-means和Louvain算法的划分类别与原始类别相似度相差较大,对于这2类算法的同质性和完整性度量应加以研究和优化。