基于多元信息融合的变压器励磁涌流识别研究

韩志

(国网冀北电力有限公司承德供电公司, 河北, 承德 067000)

0 引言

变压器是电力系统最重要、最昂贵的设备之一,变压器的安全稳定运行对于整个电力系统的安全稳定具有至关重要的意义,变压器一旦出现故障,可能会造成整个区域电网发生瘫痪事件[1]。变压器无故障时应保持变压器的正常运行,而变压器发生故障时则因将其及时停运,以防止故障扩大。变压器正常与故障状态诊断的难点主要在于励磁涌流和内部故障电流的准确识别,尤其变压器电流的采集还存在不同程度的电磁等外界噪声干扰[2]。因此,深入研究变压器励磁涌流的识别方法,从而提高变压器励磁涌流识别的准确率,对于电力系统的安全稳定运行具有重要意义。

针对变压器励磁涌流的识别,国内外学者进行了一定的研究工作。文献[3]对变压器励磁涌流的产生机理及波形特征进行了分析,比较了变压器励磁涌流波形与内部故障电流波形的差异性。文献[4]提取出变压器电流的时域和频域特征量,将支持向量机应用于变压器励磁涌流的识别。文献[5]在研究多种神经网络性能的基础上,将广义回归神经网络应用于变压器励磁涌流和内部故障电流的识别。文献[6]利用小波包变换提取变压器电流的时频域特征量,然后利用神经网络来实现特征量与电流类型非线性映射。以上文献在进行变压器励磁涌流识别时,均存在特征量类型单一和识别结果准确率不理想的问题,且未对噪声干扰情况下的变压器励磁涌流识别进行深入研究。

本文提取出时域、频域和时频域组成的多元特征向量,并将改进后的随机森林法应用于励磁涌流识别,通过不同噪声干扰强度及不同类型特征量下的识别对比分析验证了本文方法的优越性。

1 变压器励磁涌流原理分析

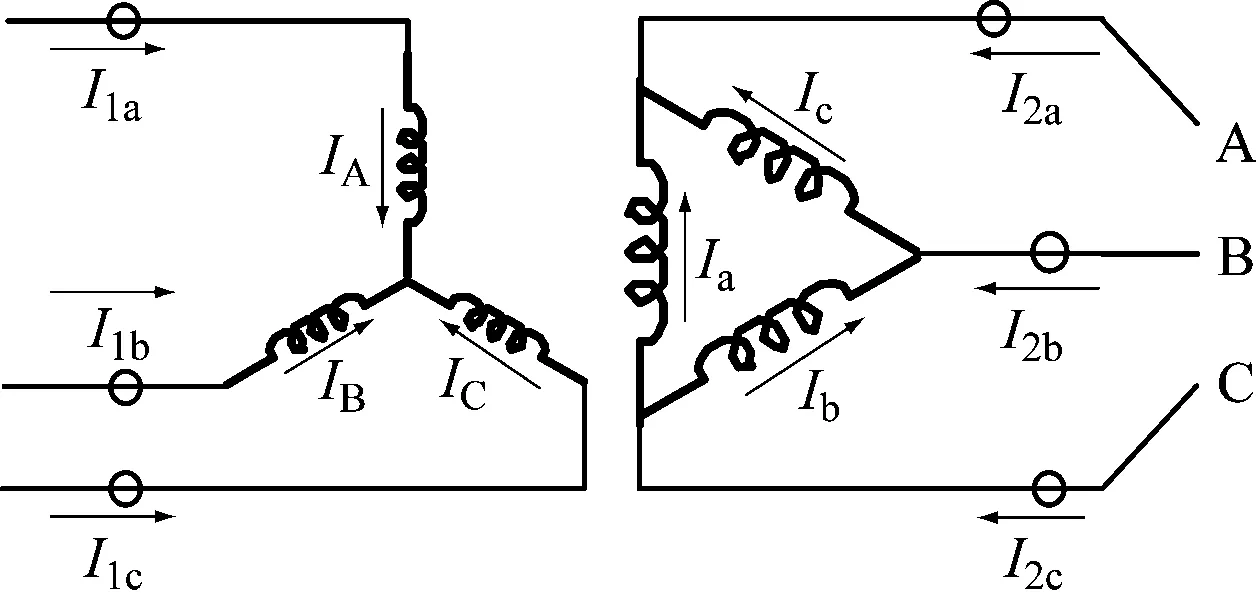
图1 变压器电流分布图

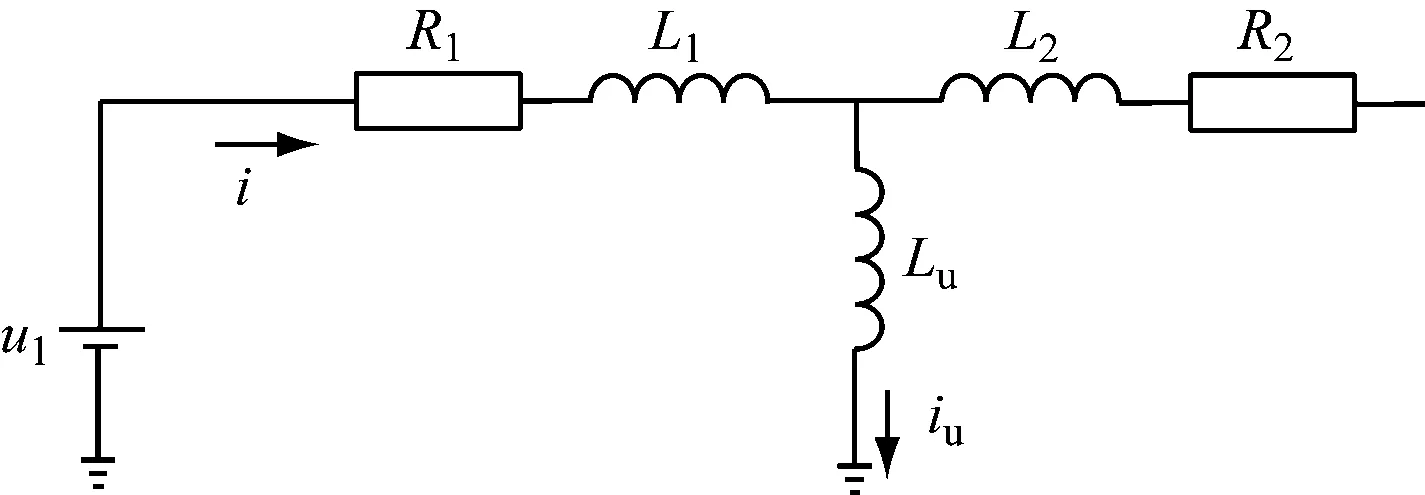
图2 变压器空载合闸等效电路模型

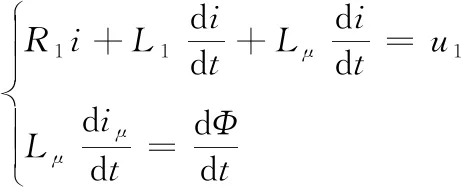
(1)

式中,R1和R2分别表示变压器一次侧和二次侧的电阻值,L1和L2分别表示一次侧和二次侧的漏感值,Lμ表示励磁电感值,u1和i表示一次侧电压和电流,iμ表示励磁电流,t表示时间,Φ表示变压器磁通。

对式(1)做拉普拉斯变换可得ABC三相的变压器磁通Φ分别为

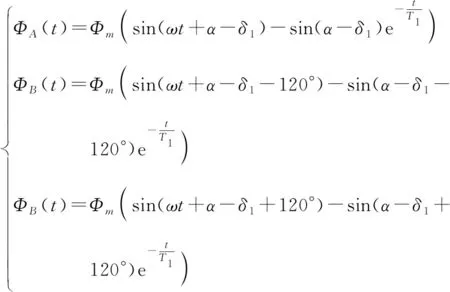
(2)

式中,Φm表示磁通最大值,ω表示角频率,T1表示衰减时间常数,α表示合闸初相角,δ1=tan-1(ωT1)。

当变压器磁通进入饱和区后,变压器的励磁电流将急剧增大,从而产生励磁涌流,磁通Φ和励磁涌流i之间的关系可表示为

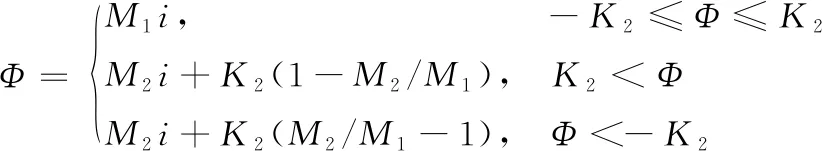
(3)

式中,K2表示磁通饱和点,M1、M2表示磁化曲线的近似折线斜率。

将式(2)代入式(3)中可求得三相励磁涌流的解析表达式,其中A相励磁涌流iA为

(4)

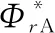
2 励磁涌流多元特征量分析

2.1 励磁涌流时域和频域相关特征量

变压器的励磁涌流与匝间短路、接地故障等故障电流在时域波形上主要区别为具有明显的间断角、偏向时间轴的一侧、发生畸变等,但励磁涌流要受到合闸角度、铁芯磁饱和以及剩磁的影响[8]。

相关性是表征2个信号波形相似性的重要方法。根据变压器励磁涌流和故障电流在波形上的不同,故障电流主要为基频正弦波,当采用正弦拟合法对其基波分量进行拟合后与原采样信号相似程度很高,而励磁涌流拟合后的曲线则相似程度很低[9],因此本文将相关性系数作为识别励磁涌流与故障电流的一个特征量。

对于采样信号x(ti)与拟合曲线y(ti),其互相关函数rxy(ti)的表达式为

(5)

式中,n表示采样总点数。

对式(5)进行归一化处理可得相关系数ρxy(ti):

(6)

当相关系数|ρxy(ti)|=1时;表明2个波形完全相同;当|ρxy(ti)|=0时;表明2个波形完全不相同;当0<|ρxy(ti)|<1时,表明2个波形存在一定程度的相似。

根据研究表明变压器励磁涌流在其峰值和间断处的基波倍频与二次谐波相位差为0°或180°,二次谐波电流I2与基波电流I1相位差θ为

θ=arg(I2)-2arg(I1)

(7)

2.2 基于小波包变换的励磁涌流时频域特征量

小波包变换是在小波变换的基础上改进而来的,它可以对信号进行更加精细的分析,不仅具有小波变换良好的时频局部化性能,而且对多分辨分析没有细分的高频部分能够进行更深层无冗余的分解,从而具有更高的时频分辨率[10]。

信号S的小波包三层分解的树结构如图3所示,其小波包函数W的表达式为

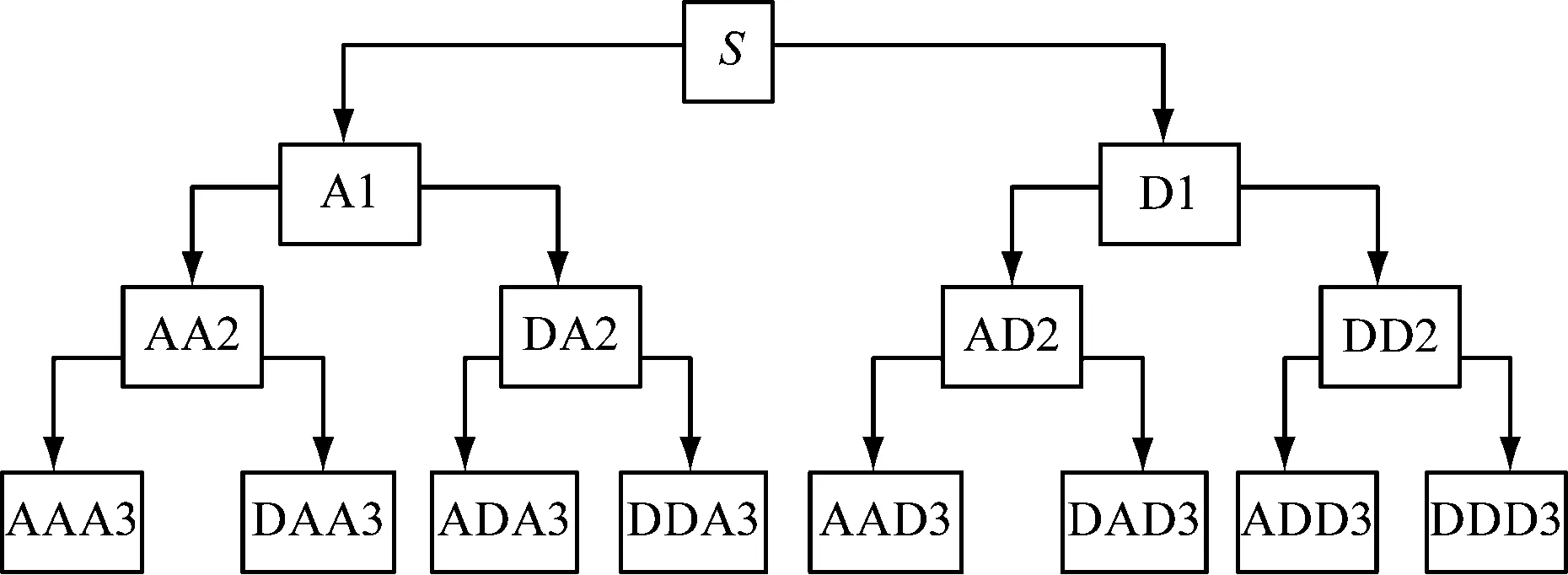
图3 小波包分解结构图

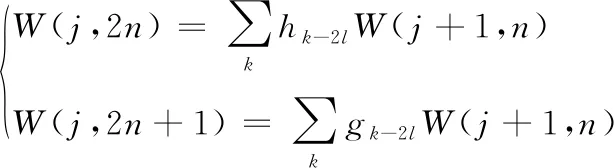
(8)

式中,j和l表示尺度系数和位置系数,n表示频率,h和g表示低通滤波器系数和高通滤波器系数。

对信号S进行i层小波包分解后,能获得2i个子频带,则S可表示为

(9)

式中,Si,j表示第i层上节点(i,j)的重构信号。

对于第3层j子频带S(3,j),其对应的小波包能量E(3,j)的表达式为

(10)

式中,xj, k(j=0,1,2,…,7;k=1,2,…,n)表示重构信号Si,j的离散点幅值,n表示采样点数。

对于第3层,其小波包总能量E表达式为

(11)

本文引入相对小波包能量,即每个子频带占第3层总能量的比例系数Eopj,其表达式为

(12)

本文提取的小波包能量时频特征量为

(13)

3 变压器励磁涌流识别数学模型

3.1 随机森林方法原理分析

随机森林算法是结合“Bootstrap aggregating”和“random subspace method”思想构造的具有多个决策树的分类算法,随机森林决策树之间相互独立,使得随机森林模型泛化性能优良[11],它具有抗干扰能力强、诊断准确率高、时间效率好等优点,已在数据挖掘和故障诊断等领域得到广泛应用,随机森林算法建模主要流程如图4所示。

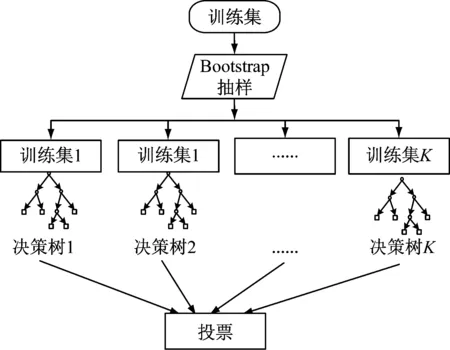
图4 随机森林建模流程图

假设自变量X训练后生成的决策树为{J1(X),J2(X),…,Jh(X)},则输出结果J(X)为

(14)

式中,Ai(x)和N(·)分别表示映射函数和示性函数,Y表示输出变量,h表示训练次数。

随机森林泛化误差与决策树的数量有关,当数量超过一定值时,泛化误差PE*趋于某一上界值[12]:

(15)

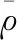
为进一步提升随机森林算法性能,本文对其做出一定的改进。对于随机森林属性特征的重要程度,本文使用信息值进行相应的评估,信息值IV的表达式为

(16)

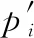
对于随机森林各决策树的投票,本文使用加权投票的形式,对于决策树Ji,其权重系数λ(i)的计算方法为

(17)

式中,ntree表示决策树的数目,OOBCorr表示袋外数据的准确率。

3.2 变压器励磁涌流识别数学模型

通过对变压器电流的分析,提取出可有效反映励磁涌流和故障电流差异性的各类型特征量。其中时域特征量选取间断角,频域特征量选取相关性系数、二次谐波幅值、二次谐波与基波相位差,时频特征量则为小波包变换提取的相对小波包能量。各特征量首先进行归一化处理,以消除特征量幅值数量级差异性对模型的影响;然后由改进的随机森林模型来表达各特征量与电流类型的复杂非线性映射关系,从而诊断出电流类型。本文基于改进随机森林法的变压器励磁涌流识别基本流程如图5所示。

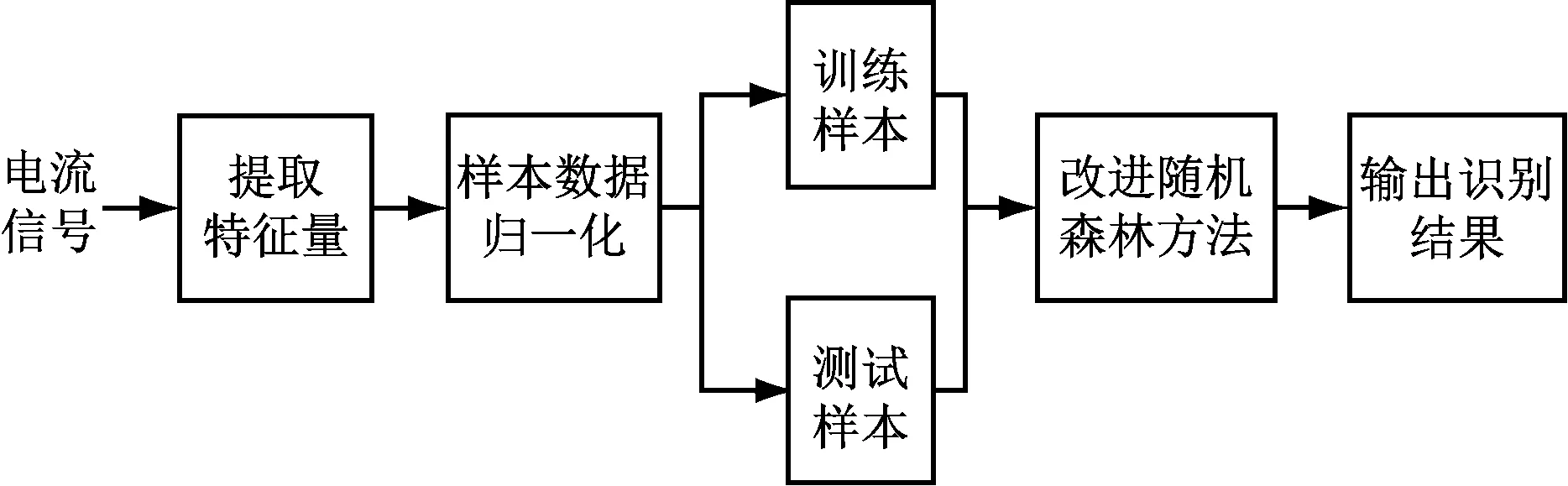
图5 本文励磁涌流识别流程图

4 算例分析

4.1 仿真模型

本文利用MATLAB/Simulink仿真软件对变压器励磁涌流和内部故障电流进行仿真分析[13]。故障电流类型包括匝间短路故障、线圈单相接地、两相短路和三相短路,仿真模型如图6所示。变压器为三相双绕组变压器,连接方式为YNd11,变比为220 kV/35 kV,额定容量为250 MVA,随机森林法决策树的数目ntree为35,最佳分裂变量数为3。励磁涌流仿真时将变压器铁芯设为饱和状态,内部故障仿真时将故障位置设置在次级绕组连接线处,某次仿真时获得的励磁涌流波形图和内部匝间故障的电流波形如图7所示。

图6 变压器仿真模型图

(a) 励磁涌流波形图

励磁涌流和匝间短路、单相接地、两相短路、三相短路的内部故障电流的样本示例如表1所示。

表1 变压器故障特征量样本示例

4.2 识别结果分析

为了验证本文改进随机森林法在变压器励磁涌流识别的有效性和具有的优势以及抗干扰能力,对仿真获得的电流施加不同程度的高斯白噪声,施加高斯白噪声后电流波形样例如图8所示,并选取常用的神经网络法、支持向量机法、未改进的随机森林法进行比较分析。其中,支持向量机惩罚因子C和高斯核函数σ分别取1.2、0.001,BP神经网络的隐含层节点数设为25,附加动量因子取0.93,学习速率取0.06,随机森林的决策树数目为35,最佳分裂决策变量数为3,最小节点尺寸为3。同一强度噪声含量下的励磁涌流和故障电流样本由图6模型仿真获得。其中,励磁涌流样本通过随机改变合闸角、剩磁和系统侧电阻值获取。4种类型故障电流样本则通过对故障位置的随机选择获得。5种类型的电流样本各获取46组,获取的样本共230组,其中200组用于训练,剩下的30组则用于测试。不同噪声含量下各方法的识别结果如表2所示。

表2 变压器励磁涌流识别结果

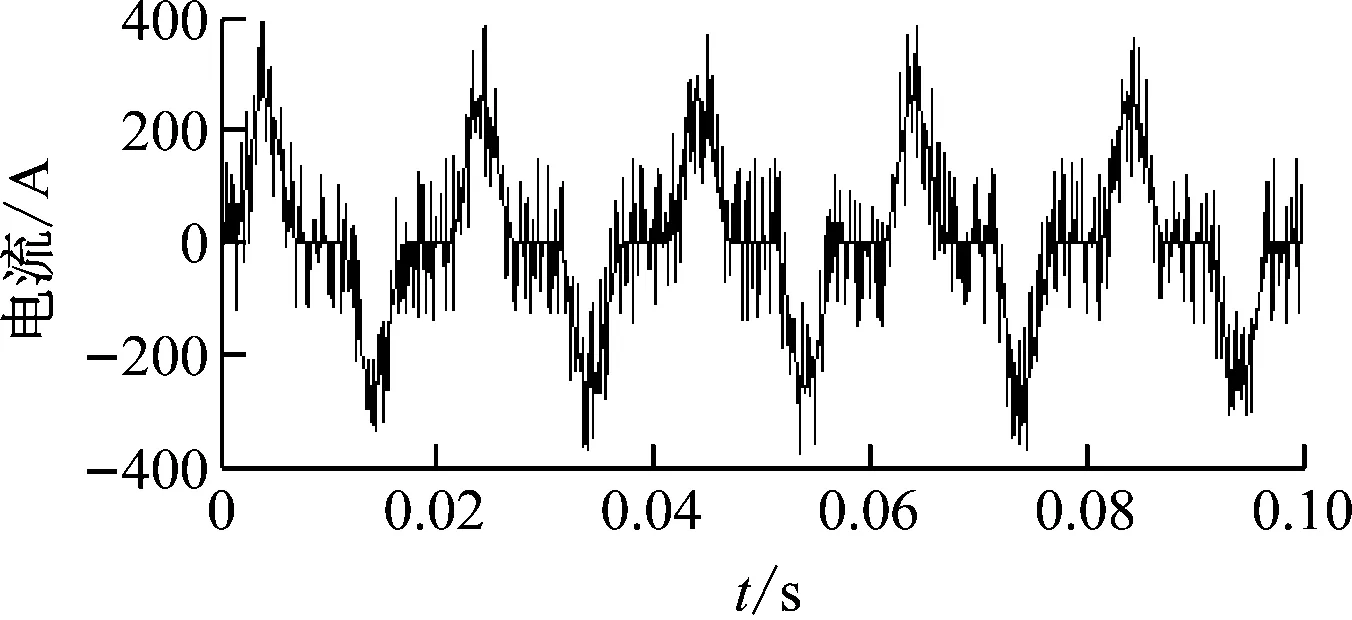
(a) 励磁涌流波形图

由表2可知,本文改进后的随机森林法在变压器励磁涌流识别中具有更好的准确性和抗干扰性,在不同强度噪声干扰下的识别准确率均是最高的,且随着噪声强度的增加,识别准确率下降速度是最慢的。本文方法在10%噪声含量下的准确率依旧有86.67%,远高于其他3种方法。随机森林法的识别能力要高于神经网络法和支持向量机法,而本文对其改进后进一步提升了随机森林法的识别性能。

另外,为进一步验证本文采用多元特征量的优越性,对采用时域、频域、时频域不同组合的特征量进行识别比较分析。时域特征量为间断角,频域特征量为相关性系数、二次谐波幅值、二次谐波与基波相位差,时频特征量为小波包变换提取的相对小波包能量,如时域与频域特征量组合的特征量为间断角、相关性系数、二次谐波幅值、二次谐波与基波相位差5个,不同类型特征量组合下的励磁涌流和故障电流各获取230组样本,200组用于训练,剩下的30组则用于测试,识别方法为本文改进后随机森林法,识别结果如表3所示。

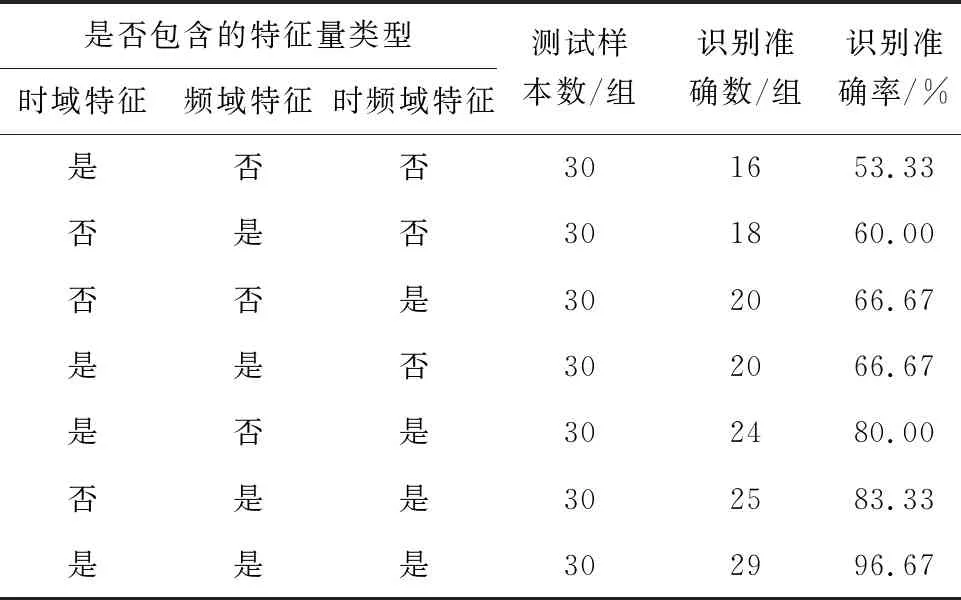
表3 不同特征量下励磁涌流识别结果

根据表3可知,采用本文时域、频域、时频域多元融合的特征量能获得更高的识别准确率,更有利于变压器励磁涌流的识别。本文提出的变压器励磁涌流识别方法能更有效地识别出变压器电流的类型。

5 总结

本文从变压器故障电流中提取出时域、频域和时频域相融合的多元特征量,提出了一种基于改进随机森林方法的变压器励磁涌流识别模型。通过变压器励磁涌流识别仿真实例的比较分析,结果表明本文方法在不同强度的噪声干扰下均能获得更高的识别准确率,且随着噪声强度的增强,本文方法识别准确率的下降速度要比其他3种方法明显更小。在强度为10%的噪声干扰下,本文方法识别准确率仍高于85%,而对于特征量的选择,本文采用的时域、频域和时频域的多元组合特征量能更好地反映电流的类型,从而使电流识别获得更高的准确率。本文励磁涌流识别模型具有优良的识别能力和抗干扰能力,可为变压器励磁涌流的识别及其安全稳定运行提供有效的理论参考和技术指导。