基于IPSO-SVM的电力输电线路隐患故障识别方法

蔡建峰, 刘明辉, 鲁杰, 李威, 钟磊, 张清敏

(1.国网冀北电力有限公司承德供电公司, 河北, 承德 067000;2.智洋创新科技股份有限公司, 山东, 淄博 255086)

0 引言

电力输电线路按照结构可分为两种结构,一是架空输电线路、二是电缆线路。输电线路在运行使用过程中,受到多种因素的影响和作用后,会形成隐患故障[1-4]。由于隐患故障的风险识别和判定标准无法统一,因此隐患故障识别结果的可靠性存在一定偏差。沈晓枉[5]为识别线路故障,以空间故障树理论为基础,提出了相应的故障识别方法;王桥梅等[6]为保证线路故障识别的精准性,依据VMD多尺度模糊熵,提出了相关的故障识别方法。上述方法均能够完成电力线路故障识别,但是对于处于隐患阶段以及早期阶段的线路故障的识别可靠性仍需进一步验证。

本文针对电力输电线路的隐患故障展开详细分析后,针对隐患故障的特点提出基于IPSO-SVM算法的电力输电线路隐患故障识别方法,改进粒子群算法(IPSO)是一种寻优算法,其在基础粒子群算法的基础上,实现算法扩展性的优化,提升算法自身的寻优效果和性能;支持向量机(SVM)作为一种典型且应用较普遍的机器学习方法,其能够以及决策边界的计算结果完成目标的分类,以此完成电力输电线路隐患故障识别。

1 电力输电线路隐患故障识别

1.1 电力输电线路隐患故障多特征提取

1.1.1 隐患故障能量特征向量计算

采用峭度、偏斜度、方差、裕度指标等多种特征量表示时域特征参数,如表1所示。

表1 特征量参数详情

但是上述特征参数存在一定局限性,因此为准确获取电力输电线路隐患故障特征频带滤波信号[7],采用均匀划分手段对所有的时域特征参数实行划分处理,其采用小波分解完成,且为正交小波。频域特征参数则采用划分后获取子带频率滤波信号描述,则基于Parseval恒等式可得出:

(1)

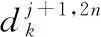
如果原始电力输电线路隐患故障特征经过小波包分解后形成的频带数量用M表示,则各个频带对应的能量计算公式为

(2)

式中,Ni表示数据长度,对应第i个子频带。

在式(2)的基础上,计算能量φi的均方根,其公式为

(3)

采用归一化的方式对能量值实行处理后可得出能量特征向量,其公式为

(4)

1.2 隐患故障多特征提取

完成Ri值的获取后,采用Hilbert包络谱奇异值对Ri的分量φ1,φ2,…,φM实行变换处理,其公式为

(5)

在式(5)的基础上,计算电力输电线路隐患故障的本征模式分量(IMF)的包络谱,其计算公式为

(6)

将式(6)的各个结果组成矩阵B,其大小为m×n,依据奇异值分解,得出存在2种正交矩阵,其分别为U=[u1,u2,…,um]∈Rm×m和V=[v1,v2,…,vm]∈Rm×n,2种矩阵均为奇异向量矩阵,且均属于B,基于此可确定:

UTBV=diag[β1,β2,…,βl]=S

(7)

式中,βi表示奇异值,其中i=1,2,…,l。基于上述公式得出B的奇异值分解公式:

B=UVTSζ

(8)

获取其对应的包络谱奇异值矩阵B,将B作为电力输电线路隐患故障识别的特征向量,输入至经IPSO优化的SVM的故障识别模型中,完成电力输电线路隐患故障分类识别。

1.3 电力输电线路隐患故障识别

1.3.1 隐患故障识别结果寻优的IPSO算法

确定其在隐患故障分类识别结果寻优过程中,惯性权值ω对其全局搜索能力存在直接关联,因此,对实行优化,形成动态惯性权值ω′,其公式为

(9)

式中,k和L均表示迭代次数,前者对应当前,后者对应最大,ωmax和ωmin均表示权值,前者为最大,后者为最小。

提升粒子群算法的全局搜索能力后,完成粒子群算法的自身优化后,为使粒子能够较快地完成全局自由隐患故障分类识别结果的搜索,对LS-SVM模型的参数实行优化,优化的参数为惩罚因子和核参数,分别用c和g表示。则IPSO对LS-SVM模型实行优化的适应度函数γ(x)的计算公式为

(10)

式中,f(x|c,g)和f0(x|c,g)均表示输出结果,前者对应实际,后者对应期望,n表示数量对应校验集样本。

如果X=[c,g]表示变量,γ(X)对X的偏导数公式为

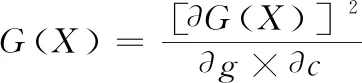
(11)

如果电力输电线路隐患故障中各个变量呈线性,γ(X)对X的偏导数公式为

(12)

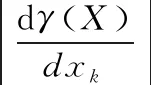
(13)

式中,粒子速度用υ(t)表示,且在t时刻,x(k|t+1)和x(k|t)均表示粒子位置,属于第k个变量,且位于个体向量中,前者对应t+1时刻,后者对应t时刻,则用于描述电力输电线路隐患故障分类识别结果更新位置。优化流程如图1所示。

1.3.2 基于IPSO-LS-SVM算法的隐患故障分类识别

通过1.3.1小节完成优化后,采用优化后的基于IPSO-LS-SVM算法完成输电力线路隐患故障分类识别。其识别分类步骤如下所述。

(1) 设c1和c2均表示初始学习因子,维数和规模分别用D和E表示,前者对应粒子搜索空间,后者对应粒子种群,对上述IPSO的参数实行初始化处理,且设定初始迭代次数为0。

(2) 对LS-SVM的待优化参数c、g以及核函数权重系数λ的取值范围进行设定,生成随机一组参数,用(c,g,λ)表示,并采用该参数表示粒子的初始位置。

(3) 求解γ(X),并将该求解结果与粒子的个体最优位置γ(pbest)进行对比,如果前者小于后者,采用xi替换上一轮的粒子位置,此时适应度函数为

γ(xi)=1-γ(p)

(14)

式中,γ(X)表示隐患故障的分类精度。

(4) 获取全局最优解。将γ(pbest)和全局最优适应度值γ(qbest)进行对比,如果前者小于后者,则采用pbest替换qbest。

(5) 完成粒子的位置、υ(t)、ω′以及c1和c2的更新。

(6) 结果输出。当γ(xi)结果满足一定精度或者迭代满足最大次数时,完成参数值输出,反之,回步骤(3)。

(7) 依据上述步骤完成基于IPSO-LS-SVM模型的构建,获取模型的最佳参数,并完成电力输电线路隐患故障分类识别。

本文在识别过程中,采用多分类器组合的方式完成隐患故障的分类诊断,多分类器的组合诊断结构如图2所示。

图2 多分类器隐患故障分类识别结构

2 测试分析

为验证本文隐患故障识别方法的应用性能和效果,将某电力企业20 km线路作为研究对象,获取线路的相关数据,数据采集过程中,为保证采集数据准确性以及全面性,结合该电力企业电力输电线线路的地理环境以及输电线路类别,设定采集线路步长为2 km,采集时间为1个月,共获取10组数据。采集的数据中包含4种电力输电线路隐患故障类别,分别为雷击、覆冰、悬挂物以及山火,分别用故障1～4表示。4类隐患故障数量分别为12个、15个、18个以及7个。上述4种隐患故障均存在发展特性,容易造成输电线路绝缘损坏、杆塔倾斜、漏电、电力运行故障等。

设最大迭代次数为180,粒子种群规模为25,学习因子c1和c2的取值分别为1.4和1.6,核参数g取15.5。

为测试本文方法优化后隐患识别的优势,获取在不同迭代次数下,对初始特征个数与特征分类后的个数进行对比分析,即验证隐患故障特征识别过程的有效性。在优化前、后,按照梯度方向,在固定维数和规模下计算t+1时刻和t时刻的个数差,获得对电力输电线路4种隐患故障识别误差结果,以此衡量本文方法优化优势。结果如图3所示。

图3 优化前后的隐患故障识别误差测试结果

由图3结果可知,本文方法经过优化后的隐患故障特征识别效果更佳,误差值均在0.06以下。

本文方法在进行输电线路隐患分类识别过程前,需先在取值范围内确定惩罚因子c的最佳取值。以隐患故障识别精度作为衡量标准,测试2种参数在不同取值下的识别精度,结果如图4所示。

图4 最优参数取值测试结果

由图4结果可得,随着c取值的逐渐增加,隐患故障识别精度发生不同波动变化,与优化前的取值测试结果相比,c取值为0.002时,隐患故障识别精度最佳,达到0.96。因此,确定本文方法的c的最佳取值为0.002,并用于后续隐患故障识别测试中。

为测试本文方法的电力输电线路隐患故障特征提取性能,以时域特征参数结果为衡量标准,4种电力输电线路隐患故障为例,采用本文方法获取表1中的时域特征参数,并计算该参数对于不同类别隐患故障的影响水平,结果取3次计算结果的平均值,如表2所示。

表2 时域特征参数计算结果

由表2结果可得,本文方法具备良好的隐患故障特征提取性能。

为测试本文方法对电力输电线路隐患故障识别性能和效果,应用本文方法在不同样本数量下,对4种电力输电线路隐患故障进行分类识别,获取识别结果,并将识别结果与实际结果进行对比,分析本文方法的识别效果,如图5所示。

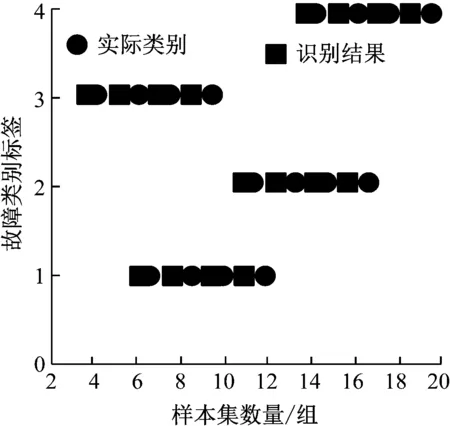
图5 电力输电线路隐患故障分类结果

由图5结果可得,随着样本数量的逐渐增加,本文方法依旧能够较好地完成隐患故障分类,并且分类结果与实际极为吻合。

电力输电线路在运行过程中会受到电磁以及自然环境中的声音干扰,导致采集的电力输电线路数据中存在一定程度的噪声。因此,为进一步衡量本文方法的隐患故障识别效果,获取本文方法在不同信噪比噪声下,对于电力输电线路隐患故障的识别结果,如图6所示。

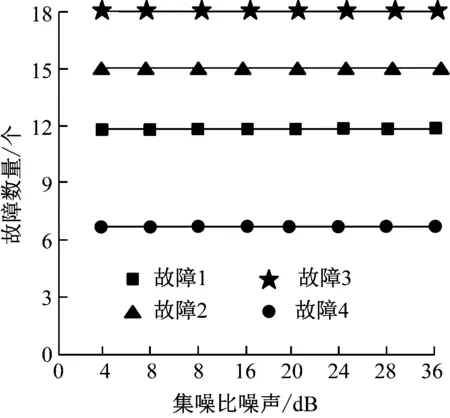
图6 电力输电线路隐患故障的识别结果

由图6结果可得,随着不同信噪比噪声的逐渐增加,4种电力输电线路隐患故障的识别结果均与实际结果数量一致,表示本文方法能够可靠完成电力输电线路隐患故障的识别,为电力系统的运行管理提供可信度较高的隐患故障情况结果,为电力系统的安全运行提供可靠依据。

3 总结

本文为准确识别输电线路的隐患故障,提出基于IPSO-SVM算法的电力输电线路隐患故障识别方法,经过双重优化后,具备更佳的隐患故障识别性能,能够准确完成隐患故障中的多特征提取,保证隐患故障的识别效果,为电力系统的安全运行提供了可靠依据。