电力市场环境下系统容量价值分析测算

詹卫许, 王舒杨, 张建中, 郑景立, 司福利, 张沛

(1.南方电网数字电网研究院有限公司, 广东, 广州 510000; 2.天津弘源慧能科技有限公司, 天津 300000)

0 引言

2020年8月美国加州紧急停电、2021年2月美国得州轮流停电[1]、2021年10月中国多省有序用电或拉闸限电等全球电力市场事故使电力系统发电容量的充裕性问题成为讨论的热点之一。在电力市场环境下,如何确保发电容量充裕性是一个极具挑战的问题[2],系统容量价值的分析与测算对不同保障充裕性的机制有关键指导作用。本文从基本的供需理论出发,提出系统容量价值的测算方法,并通过算例验证本文方法的有效性。

1 电力系统容量价值的作用

在全球电力工业的重组进程中,现货市场建设是各国电力市场的共同部分,其理论基础是基于短期成本竞争的实时电价理论。随着风、光等新能源大规模接入,电力系统对灵活性的需求急剧上升[3],现货市场无法区别不同类型机组技术特征及价值贡献的问题愈加严重。采用安全约束机组组合、安全约束经济调度等短期模型出清的现货电价,在激励新容量投资、防止调节资源提前退役等方面的作用存有争议。为了保障电力的长期可靠供应,国外电力市场设计了不同的容量充裕度机制,帮助发电机组尤其是边际机组回收容量成本。

1.1 容量补偿机制

智利、阿根廷等国家采用的容量补偿机制是由监管机构设定补偿标准,直接向市场中符合条件的容量提供者支付容量费用[4]。容量价格主要取决于系统峰荷时段运行的边际机组投资成本,而各机组的最终补偿收入与峰荷时段的出力有关,体现了发电资源对系统充裕性的贡献。

1.2 容量市场机制

美国PJM、英国等地区运行了独立于能量、辅助服务交易的集中式容量市场[5],该市场以机组的可用装机容量作为标的,由系统运营商确定需求曲线、容量提供者申报供应曲线,通过最小化容量采购成本进行市场出清,中标的资源可获得容量收入。

1.3 可靠性期权机制

意大利、爱尔兰等国家在单一能量市场基础上推行可靠性期权机制,其本质是一种看涨期权金融产品[6]。期权的买方是运营机构或用户,通过签订合同向发电机组支付期权保费,当现货市场价格高于合同执行价时,有权要求发电商返回收益差值。

尽管上述容量机制的原理各有差别,但都急需一种有效核定系统容量价值的方法,指导并优化不同机制的实际应用。测算准确、合理的系统容量价值,能够直接决定容量补偿机制中补贴标准的设置,或作为可靠性期权中协议年度保费的重要参考,详细类型的机组只需要结合峰荷时段的出力情况即可量化对充裕度的贡献值。容量市场的出清模式实际上与核定系统容量价值的方法十分接近,其主要区别在于前者的供应曲线由市场主体自行申报,因此本文核定的系统容量价值可用于检验容量市场出清价格是否合理、检测市场主体是否滥用市场力等评估环节。

随着间歇性可再生能源渗透比率不断提高,系统容量价值的研究将具备更广泛的应用场景。国际能源署(IEA)在2020年全球发电成本报告中提出,为了公平衡量不同发电技术在系统服务上的贡献,可通过测算系统容量价值,进而根据机组的有效可用率量化特定技术容量价值,改进传统的平准化成本(LCOE)竞争力度量标准。鉴于当前国内外文献对系统容量价值的测算研究较少,本文从经济效率最优的层面出发,提出一种基于供需理论的测算方法,通过生产模拟与成本分析,形成系统容量需求、供给曲线,求取均衡点并最终核定系统容量价值。

2 基于供需理论的测算方法

本文基于微观经济学的供需理论,首先通过最大化消费者福利绘制容量需求曲线,然后对现有机组、规划机组进行发电长期成本分析,形成容量供给曲线,在以容量为横轴、价格(成本)为纵轴的坐标系中,令曲线相交得到供需平衡点及其对应价值。以下是具体测算步骤。

2.1 确定失负荷期望目标值

首先通过新建边际机组容量成本(CONE)、失负荷价值(VOLL)求得消费者福利最大化时的失负荷期望(LOLE)。

定义消费者的净收益Rnet为

Rnet(k)=R-CB(k)-CE(k)

(1)

其中,k表示系统总容量,R表示消费者在可靠电力供应下的收益,假设为常数,CB表示停电成本,CE表示总电力成本。

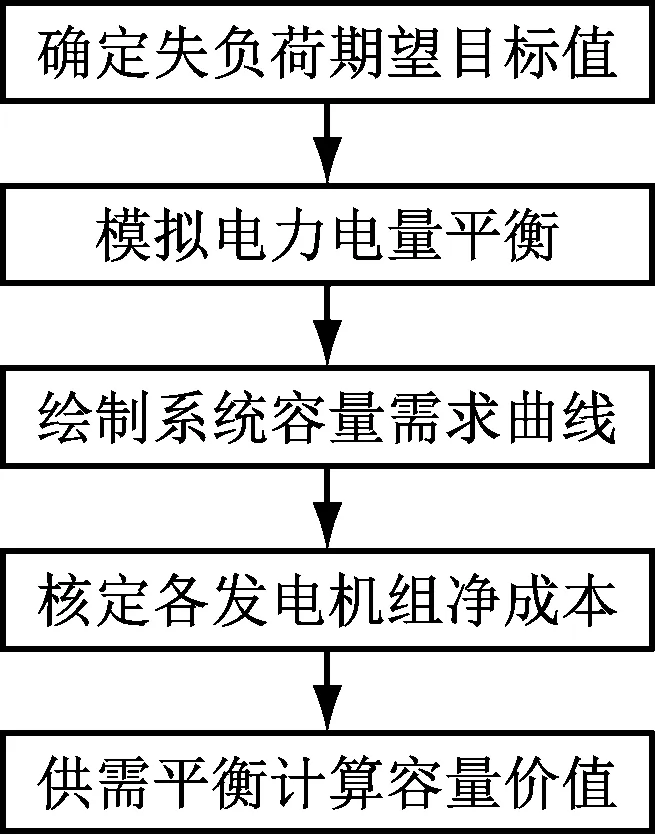
图1 容量价值测算步骤

为求得极值,等式右端对k微分并令之为0,得到:

(2)

此时,式(2)左端是增加单位容量的电力成本,右端是增加单位停电造成的经济损失。

采用Eloss表示停电电量,则有总停电成本如式(3):

CB(k)=Eloss×VOLL

(3)

式(3)两端进行对系统总容量求微分,可得:

(4)

根据式(5)所示的失负荷期望定义,可进一步得到新建边际机组容量成本,

(5)

即新建边际机组容量成本为

(6)

2.2 模拟电力电量平衡

将步骤1确定的LOLE作为可靠性标准,采用随机生产模拟进行电力电量平衡计算,得到满足可靠性标准时系统所需的总容量。本文采用等效电量函数法进行随机生产模拟[7],具体过程如下。

(1) 形成原始等效电量函数

定义持续负荷曲线为t=F(x),自变量是x,函数值是t,F(x)是一个减函数。曲线上的任意点(x,t)表示系统负荷大于或等于x时的持续时间为t。设xmin和xmax是负荷的最小值与最大值。用Δx表示常规机组容量的最大公因数,记NE=(xmax-xmin)/Δx,NE是整数。将持续负荷曲线F(x)中的x轴按Δx分段,得到离散化的电量函数为

(7)

其中,x0=xmin,xk+1=xk+Δx,k=0,…,NE-1。

(2) 计算各机组发电量

按照新能源优先、火电机组按变动成本由小到大的带负荷顺序,依次投入发电机组运行,计算发电量。第i台发电机组的发电量G应根据等效电量函数E(i-1)(j)来进行计算:

(8)

(9)

式中,Ji-1表示前i-1台发电机组容量之和所占的步长,对第1台发电机组而言,E(i-1)(j)表示原始等效电量函数,pi表示发电机组i的可用率,Ci表示发电机组i的容量。

(3) 修正等效电量函数

第i台机组投入运行后,利用卷积公式修正等效电量函数:

E(i)(j)=piE(i-1)(j)+qiE(i-1)(j-Ki)

(10)

式中,Ki=Ci/Δx

(4) 计算可靠性指标LOLE

(11)

若LOLE小于或等于可靠性标准,则结束模拟;否则,新增CONE最小的边际机组1台,返回第(2)步,迭代计算,直至LOLE满足可靠性标准,得到此时的系统总容量即为目标容量值TC。

2.3 绘制容量需求曲线

根据步骤2所得结果可绘制系统静态的垂直容量需求曲线,即在横坐标为容量、纵坐标为价格的坐标系中,目标容量值TC左侧的价格设为较高的上限(比如CONE的若干倍),目标容量值TC右侧的价格设为较低的下限(比如0)。垂直曲线下价格的弹性系数为0,但是电力市场的实际情况表明负荷有较强的价格反映。从国外实践来看,美国(PJM、纽约、新英格兰)、英国等地区建立的容量市场,为了表征容量需求随价格变化的趋势,采用了有弹性的、倾斜向下的需求曲线进行容量的集中采购。如图所示,倾斜曲线经过点(0.95*TC,1.5*CONE)、(TC,CONE),当系统容量小于目标值时,价格低于上限,当系统容量大于目标值时,价格高于下限。

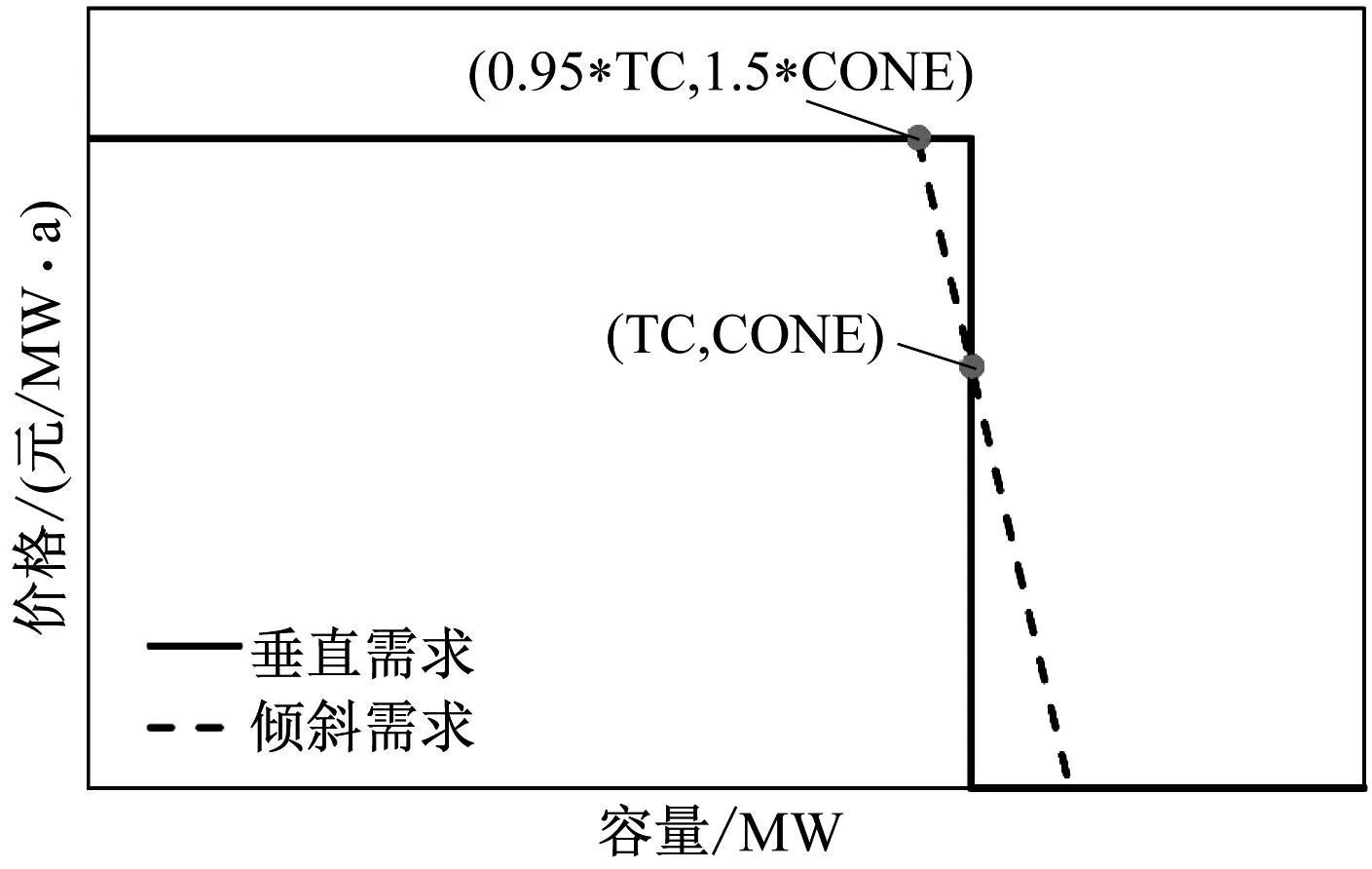
图2 需求曲线

2.4 计算不同类型机组净成本

对系统中现有发电机组的单位容量净成本(元/MW·a)进行测算,净成本等于机组投资成本的折旧值加上年固定运行维护成本,再减去发电利润。本文采用年数总和法对固定资产进行折旧,该方法是将固定资产原值减去残值后,以剩余可使用年限与逐年使用年限数字之和的比值作为当年折旧率计算折旧额。考虑资金时间价值影响因素后,发电机组固定资产折旧计算模型为

(12)

式中,I0表示固定资产初始投资,θ为残值率,Y表示固定资产折旧年限,r为资本金成本率。

2.5 供需曲线相交得到平衡点

根据步骤4的计算结果,按照净成本从小到大的顺序排列形成系统容量供给曲线,如图3所示,每段阶梯曲线的长度为同类型机组的总容量。供给曲线、需求曲线相交之处即为系统平衡点,平衡点对应的价格即为当前系统容量价值。

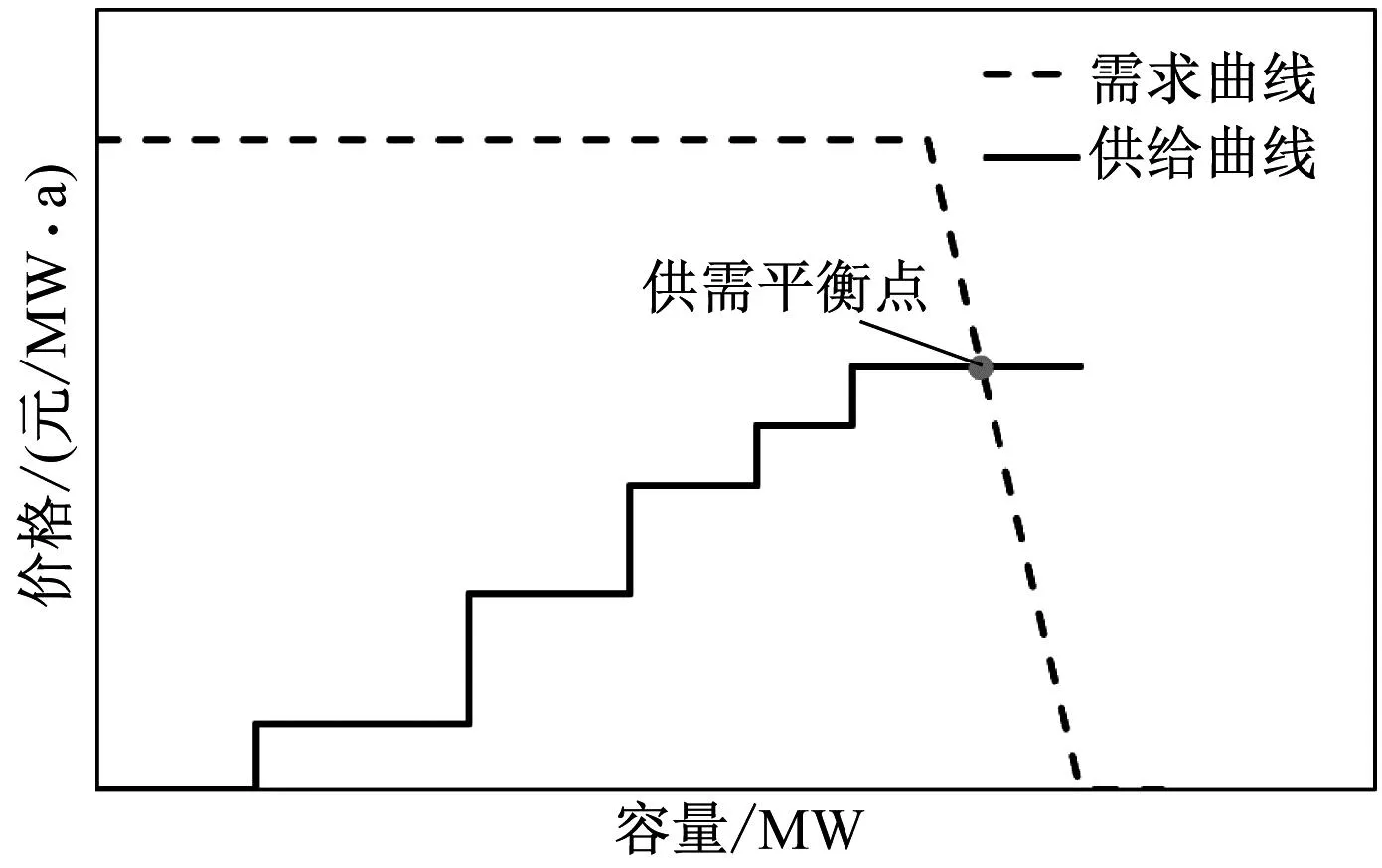
图3 供需曲线相交

3 算例分析

为说明方法的有效性,以一个简单系统为例测算容量价值。该系统年最大发电负荷为10 000 MW,持续负荷曲线如图4所示。发电端有新能源容量3000 MW,传统火电机组11 200 MW(含燃煤1000 MW、600 MW、300 MW各4台、4台、6台,燃气400 MW、100 MW各6台)。新能源机组的容量可信度取30%,火电机组的强迫停运率均取5%,已服役年限均为10年,资本金成本率为5%。详细参数见表1。

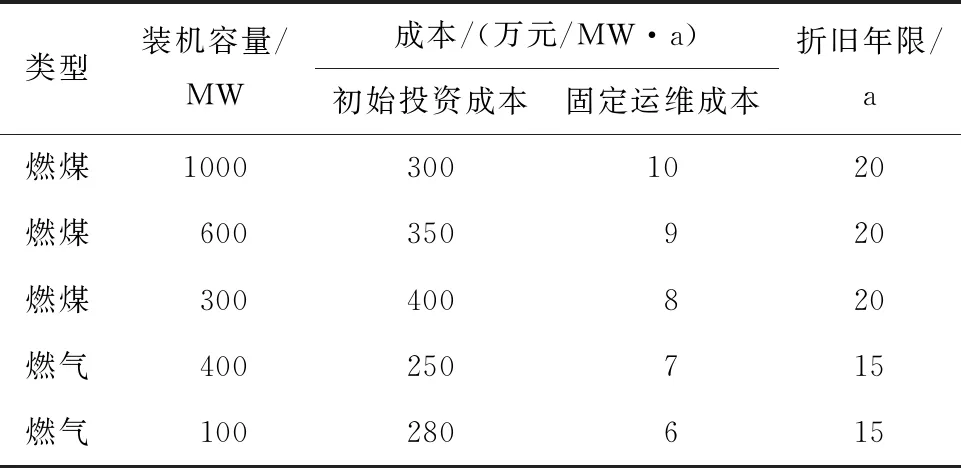
表1 火电机组参数

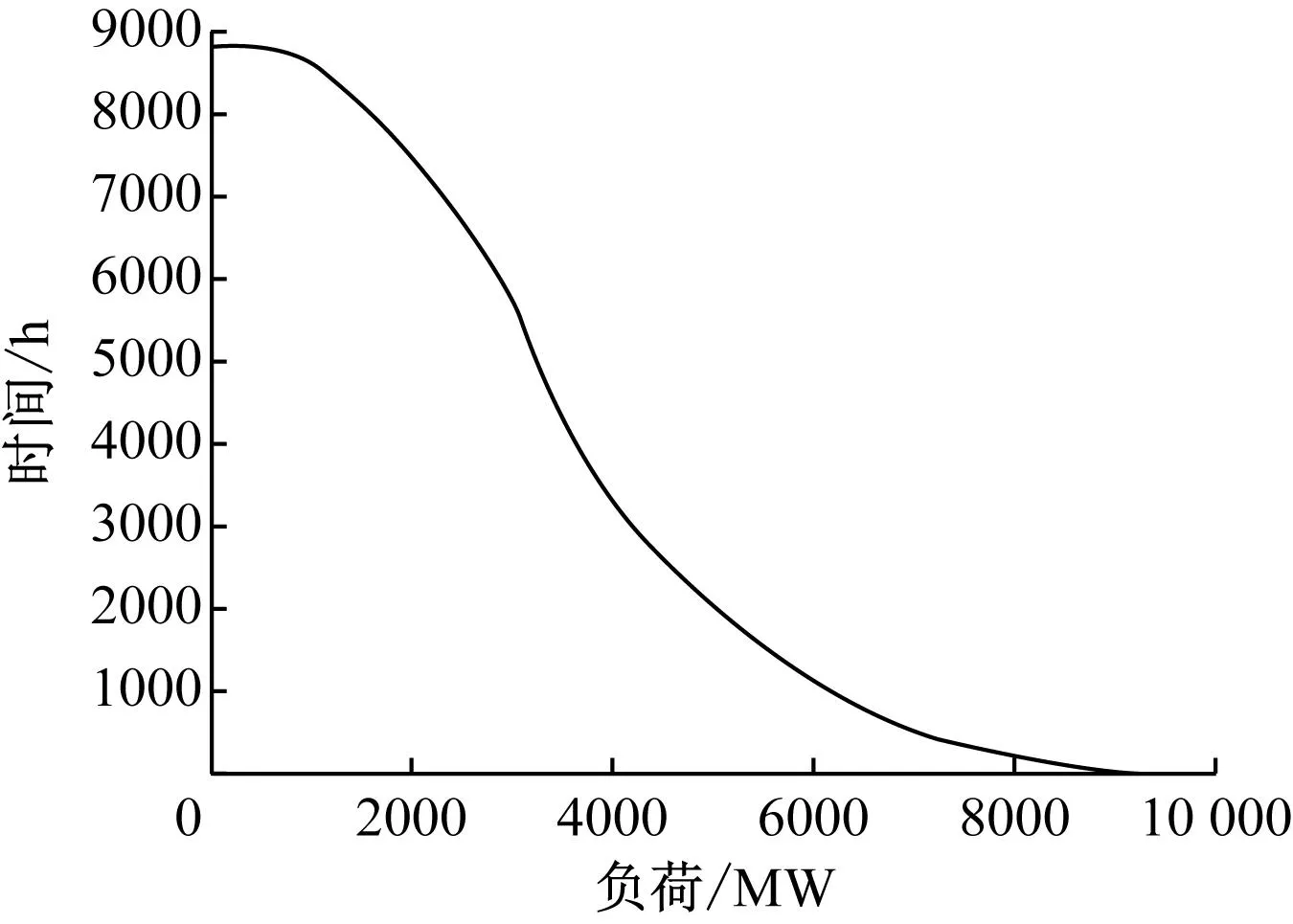
图4 持续负荷曲线

本案例中,设定失负荷价值VOLL=4万元/MWh,火电机组生产模拟的带负荷顺序依次为:燃煤1000 MW、燃煤600 MW、燃煤300 MW、燃气400 MW、燃气100 MW。新建发电容量选择初始投资成本最低的400 MW燃气机组,根据投资成本年化值、运维成本固定值得到投产年的CONE=32.73(万元/MW·a),因此:

(13)

通过等效电量函数法进行随机生产模拟,得到当前系统中LOLE=25.31(h/a),不满足可靠性目标。逐次增加400 MW燃气机组1台,继续进行随机生产模拟,记录系统扩容后更新的LOLE值。实验表明:当新增机组数量为5台时,LOLE=8.69;当新增机组数量为6台时,LOLE=8.04。可知,取新增数量为6时满足可靠性要求,此时系统总装机容量为16 600 MW。各类型机组年发电量如图5所示。

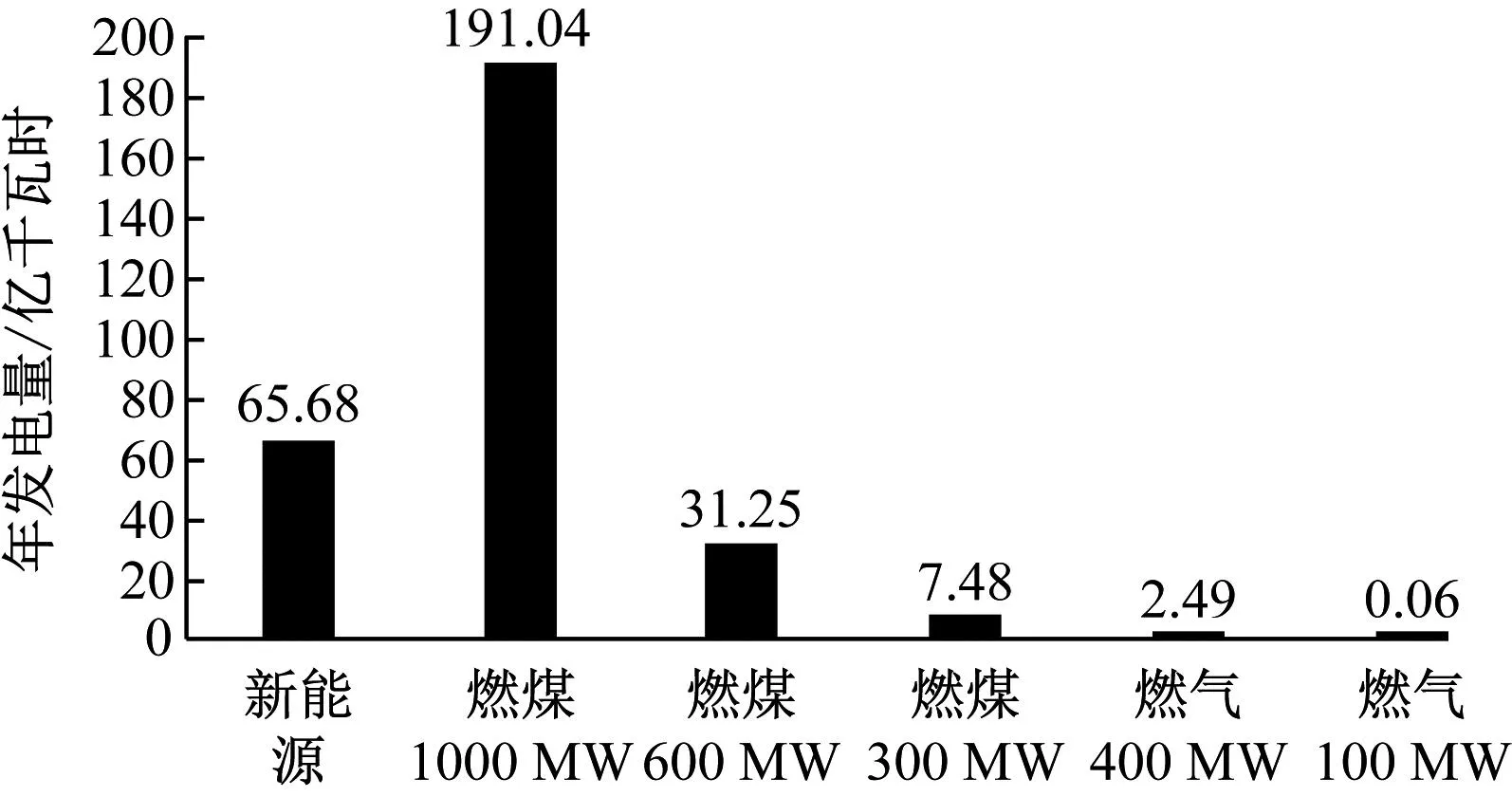
图5 各类型机组发电量

假设各发电机组在电量市场的度电平均纯利润均为50元/MWh,结合上述发电量数据,可计算各类型机组的年发电净收入。进一步,计算机组净成本为初始投资成本折旧年值,加上年固定运维成本,再减去年发电净收入,形成绘制容量供给曲线所需的数据如表2所示。

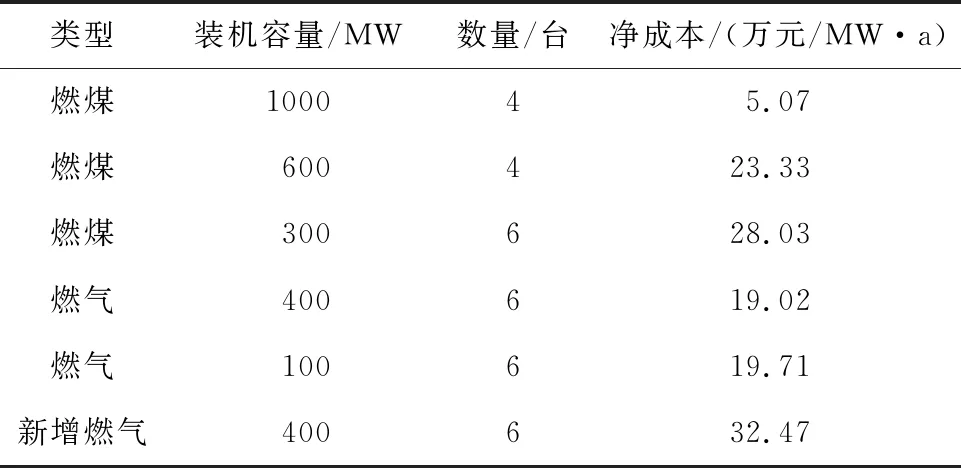
表2 容量供给曲线数据

根据以上结果,绘制该系统的容量需求、容量供给曲线如图6所示,易得曲线的交点为(16 600,32.47),因此该系统的容量价值为32.47(万元/MW·a)。结合初始条件中的机组可用率,本算例新能源机组的容量价值为0.3×32.47=9.74(万元/MW·a),火电机组的容量价值为0.95×32.47=30.85(万元/MW·a)。

图6 容量供需曲线

4 总结

本文基于供需理论提出了一种量化系统容量价值的方法:在需求层面,以最大化消费者福利为目标,计算经济最优的LOLE,并通过随机生产模拟转化为装机容量需求;在供给层面,对系统中的实际发电资源进行长期成本分析,折算年度净成本并形成优先顺序表。需求与供给的均衡点反映了最佳容量水平对应的系统容量价值,研究结果对容量补偿、容量市场、可靠性期权等充裕度机制的实际应用有重要指导意义。

对电力市场化改革的效益来说,系统容量规划带来的提升要远大于短期的经济调度。本文的研究提供了一种从经济效率层面分析最优规划水平及其边际成本的思路,更深入的研究可以围绕各个测算步骤的技术环节展开。