基于预测堵车信息的路径动态规划系统

侯辰飞, 朱健慧, 刘可昕, 杨峻, 刘蕊

(1.兰州交通大学, 机电工程学院, 甘肃, 兰州 730070;2.南京理工大学, 机械工程学院, 江苏, 南京 210094)

0 引言

路径规划是研究无人驾驶领域的一个重要环节,也是智能交通系统的重要组成之一,合理的规划方案极具现实应用意义。近年来,国内外学者将Floyd算法[1]、Dijkstra算法[2-3]、A*算法[4-5]、粒子群算法[6-7]、遗传算法[8-9]等各类算法用于路径规划,并通过改进使之具有更好的应用效果。但不少规划算法实时性较差,为此本文引入ARIMA-WNN组合预测模型对未来道路交通流量进行预测,基于预测数据对道路进行动态规划,解决路径规划中的滞后性问题。

1 系统结构

本文提出的规划系统由汽车、交通流量监测设备、导航中心等3部分组成。交通流量监测设备用于路口流量的实时记录,并每隔一段时间将数据发送至导航中心,导航中心用于接收监测设备发送的流量数据并依据流量数据进行规划。

2 ARIMA-WNN加权预测模型

2.1 ARIMA模型

整合移动平均自回归(ARIMA)模型结构简单,具有良好的可靠性,是重要的时间序列预测方法。对于短时期的时间序列分析适用性好,但前提是输入的时间序列必须是稳定的。模型的基本思想是将被预测单位随着时间的向后推移产生的新序列作为一个随机序列,假设随机序列是线性且平稳变化的,则近似描述这个随机数列,利用序列的现在值及过去值预测未来值,数学表达式通常为

(θ1εt-1+θ2εt-2+…+θqεt-q)

(1)

2.2 小波神经网络预测模型

小波神经网络以BP神经网络的拓扑结构为基础,以小波基函数为隐含层节点的传递函数,在信号前向传播的同时误差反向传播[10]。小波神经网络的拓扑结构如图1所示。

图1 小波神经网络拓扑结构

图1中,X、Y分别为小波神经网络的输入、输出参数,ωij、ωjk均为小波神经网络的权值。

输入xi(i=1,2,…,k)时,隐含层的输出公式为

(2)

式(2)中,bj为小波基函数的平移因子,aj为小波基函数的伸缩因子,hj为小波基函数。本文采用Morlet母小波基函数,其公式为

y=cos(1.75x)e-x2/2

(3)

小波神经网络的权值修正与BP的修正算法类似,采用梯度修正法修正网络权值和基函数参数。

神经网络的训练时,应按照以下顺序进行。

第一步:网络初始化。

第二步:利用训练集样本训练神经网络。

第三步:计算预测输出值和误差。

第四步:根据网络输出和期望输入的误差来修正权值和小波函数的参数,进一步逼近期望值。

第五步:利用测试集样本测试精度。

第六步:判断是否满足算法结束条件(达到设定的迭代次数或期望精度),不满足则返回第三步。

小波神经网络算法流程如图2所示。

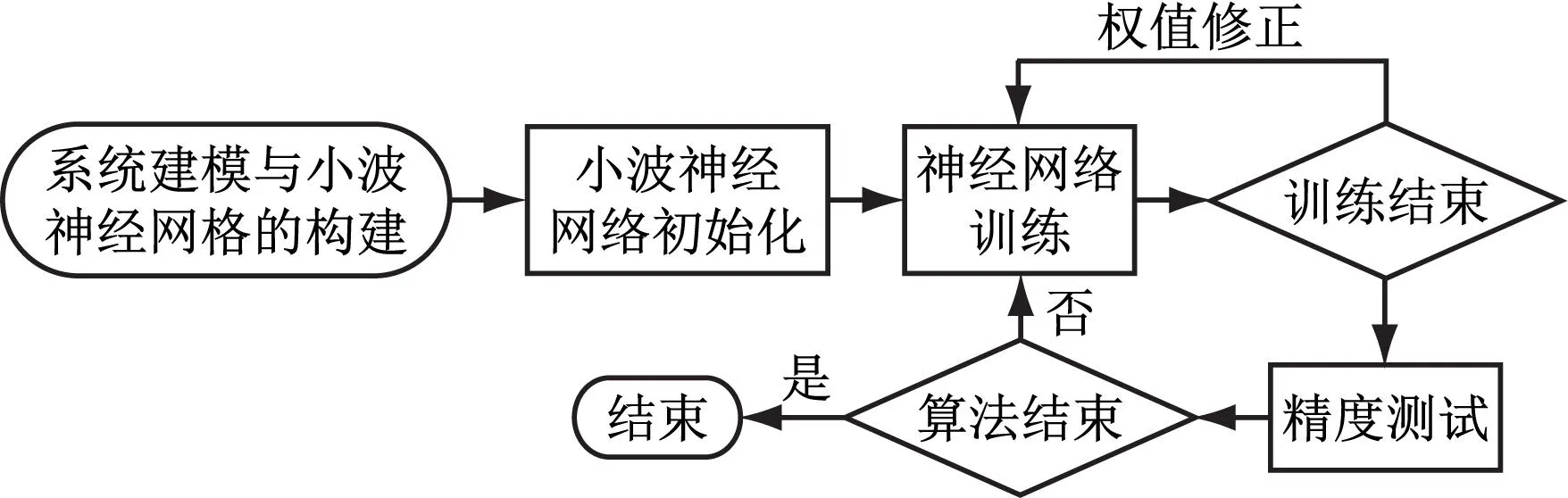
图2 小波神经网络算法流程

2.3 组合预测模型

ARIMA仅能对交通流量的线性部分进行预测分析,无法分析非线性部分,数据挖掘能力一般,而WNN对数据的非线性成分有良好的挖掘能力。本文使用ARIMA-WNN组合预测模型[11],使2种模型优势互补,综合利用历史数据中的线性和非线性部分。

利用ARIMA对原始观测数据Q={Q1,Q2,…,Qt}进行拟合,得到拟合序列P={P1,P2,…,Pt},将两序列相减得到ARIMA的残差序列E={E1,E2,…,Et},其中:

Et=Qt-Pt

(4)

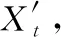
(5)

组合预测模型的流程如图3所示。

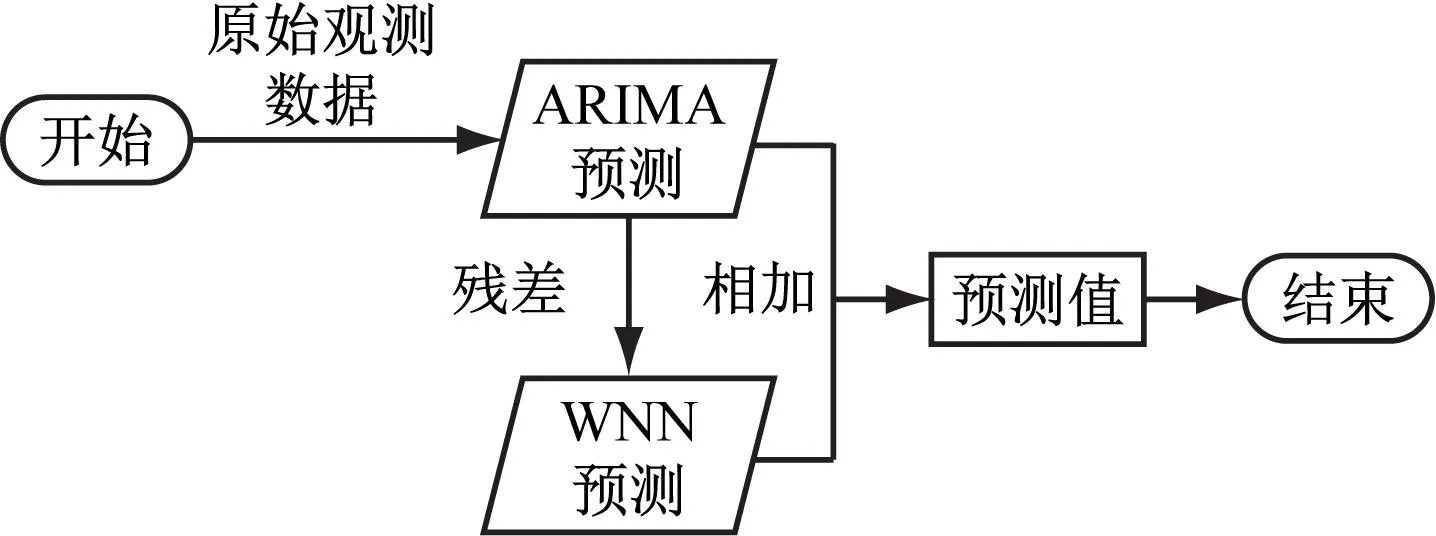
图3 ARIMA-WNN组合预测模型流程

根据图3的预测流程,首先确定预测间隔。不同时间下对同一路段进行预测,每次的预测结果都不相同,可能导致同段路径的优化方案也不同。为了避免算法的灵敏度过高,以s作为1个子时间段g,多个子时间段组成1个父时间段G,假设1个父时间段由y个子时间段组成,即Gy={g1,g2,…,gy},共涵盖s×y。要求组合预测模型每s×y进行1次预测,每次预测s×y的交通流量,牺牲部分动态性换取稳定性。

其次,确定s和y预测数据是导航中心进行局部优化的基础,预测越准确、稳定,优化的可靠性越高。本文选取15 min作为1个子时间段,即s=15,计算Gy内预测数据的平均绝对误差MAE、平均绝对百分比误差MAPE和均方根误差RMSE,结合生活实际路口情况和数理基础,倘若Gy满足:

(6)

则认为Gy={g1,g2,…,gy}是一个有效预测时间段,该时间段内的预测结果准确性高,可以为后续的局部优化提供数据基础。

每个指标的计算公式如下:

(7)

(8)

(9)

式(7)～式(9)中,n为样本数。

3 堵车情况下路径动态规划

3.1 堵车损耗

确定堵车损耗的关键在于确定发生拥堵的车辆数量。本文通过组合预测模型预测未来交通流量,基于预测数据判断未来发生拥堵的车辆数量,计算方法如下:

cm,i=nm,i-nm

(10)

式(10)中,cm,i为i时刻m节点发生拥堵的车辆数量,nm,i为i时刻m节点的车辆数量,nm为m节点所能承受的不发生拥堵的最大车辆数。假设只在节点位置发生堵车,并参考文献[12]中车辆在i时刻通过堵车节点时会有额外损耗。额外损耗计算方法如下:

km,i=α×cm,i

(11)

式(11)中,km,i为i时刻通过节点m节点的额外损耗,α为单位额外损耗。

3.2 路径规划

本文采用改进的Dijkstra算法结合未来交通流量预测进行路径规划。传统Dijkstra算法的基本思路是从起点开始,每次向一个距离最短的点扩展,与其相邻的点的距离也随之更新。由于所有边的权值均不小于0,不存在一个距离更短的、没扩展过的点,因此这个点的距离不再发生变化,保证了算法的正确性。在二维空间中,假设起点为m,终点为n,每个点都有一对规定的坐标(kn,ln),其中,kn为m到n的最短距离,ln为m到n的最短路径中的上一节点,则m到n的最短路径求解步骤如下。

第一步:对起点、终点及其他点坐标进行初始化,标记起点为m,记j=m,其他所有节点不作标记。

第二步:对所有已标记的点k到与其直接相连的未标记的点n的距离进行检验,即kn=min{kn,dkn+kn},其中dkn表示k到与其直接相连的点n的距离。

第三步:选取点w,使ki=min{kn},其中n表示所有未标记的点,则w为最短路径上的一点,更新其状态为已标记。

第四步:对所有点进行遍历,直至所有点均已被标记,否则j=w,返回第二步。

传统的Dijkstra算法没有考虑道路堵车情况的影响,导致规划出的路径存在一定的滞后性,因此本文通过考虑未来道路堵车情况,使规划更加合理,减少滞后性,其中规划步骤如下。

第一步:使用Dijkstra进行初始的路径规划。

第二步:依据正常情况下汽车的平均行驶速度依次计算到达初始路径上各个节点的时间,到达时间大于其中一个有效预测时间段的则不纳入考虑。利用历史数据对一个有效预测时间段内可能通过的节点的交通流量进行预测,再结合预测结果判断车辆到达某节点时是否会发生堵车,倘若发生堵车则赋予该节点堵车损耗,并将该节点和周围r内的所有节点加入集合H中。计算H中所有节点的到达时间,并依据到达时的交通流量判断到达时是否会发生堵车,倘若堵车则同样赋予该节点堵车损耗。最后使用Dijkstra算法对该区域进行局部优化。

通过流量预测发现车辆行驶至X节点时会发生堵车现象,计算X周围节点的到达时间并判断是否会发生堵车,发现其周围的节点P、Q同样发生堵车,赋予节点X、P、Q各自的堵车损耗,结合堵车损耗进行路径的局部优化。

第三步:倘若车程大于一个有效预测时间段,则在第一个有效预测时间段驾驶结束后,重复第二步,把此时的位置作为第二步的起点。

4 实验结果

以某区域道路信息为例进行实验分析,道路的无向图如图4所示。

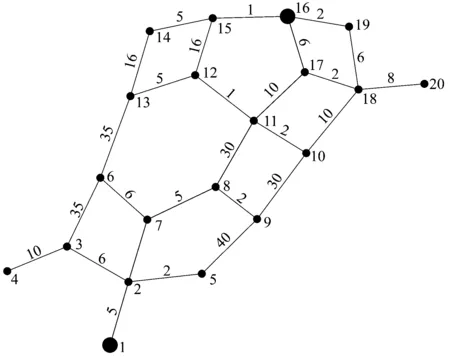
图4 道路无向图

图4中,1为起点,16为终点,以道路长度(km)为权值,范围内共20个节点。调用路口交通流量监测系统中的历史数据,以节点7为例,历史数据如图5所示,其余节点的计算与节点7相同。

图5 某路口实际交通流量

通过图5可主观判断该时间序列是平稳的,需通过ADF单位根检验法对其进行单位根检验,得到p=0.022<0.05,确定为平稳时间序列,再利用SPSSAU确定当p=1、q=1时模型拟合最好。最后对残差做Q统计量检验,Q6=0.683,p6=0.409>0.1,在0.1的显著性水平下不能拒绝原假设,即模型残差是白噪声,模型基本满足要求。因此,每15 min为1个时间段,可利用ARIMA(1,1,0)模型预测得到未来的交通流量。

建立ARIMA-WNN组合模型,步骤见2.3节,权值选择为0.01,参数学习率为0.001,迭代学习次数为100。

最后依据式(6)确定有效预测时间段Gy,若y的取值为5,则有效预测时间段为75 min。有效最终拟合效果见表1。

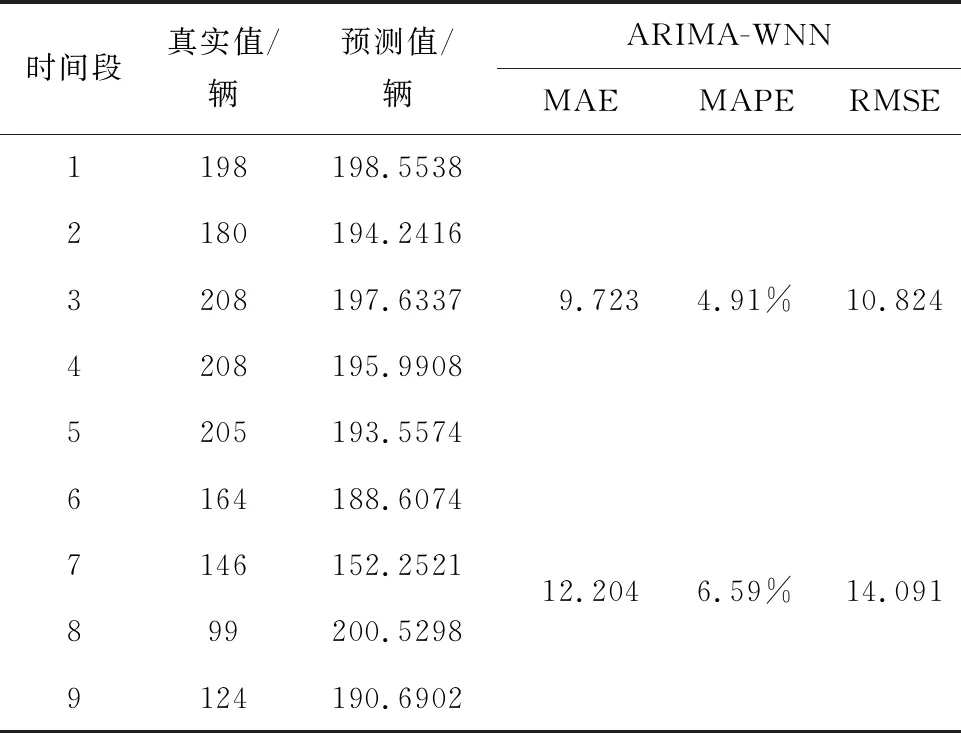
表1 ARIMA-WNN拟合效果表

由表1可知,有效预测时间段内的MAE、MAPE、RMSE值均较小,预测效果较好,数据的准确性为后续的路径规划奠定了基础。

本文使用Dijkstra算法进行全局规划,确定最短路径为91 km。初始路径如图6所示。

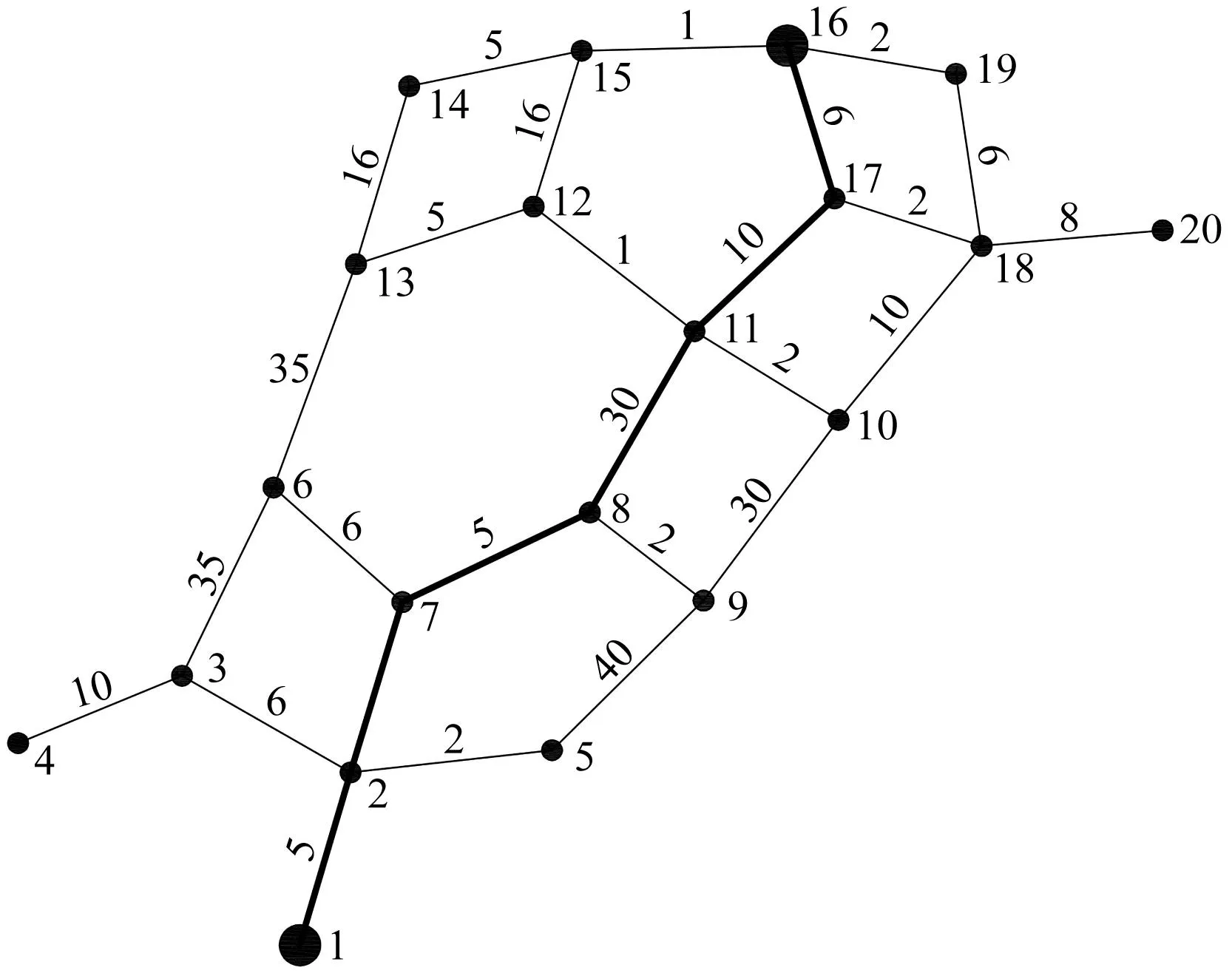
图6 初始路径

结合预测数据对路径进行局部优化得到:当节点7不发生堵车时最大车辆数量为40,单位额外损耗α=0.032,车辆的平均行驶车速为40 km/h,75 min内车辆可到达节点5与11之间。当车辆开始出发后约1 h到达节点7,则可求得c5,60≈156,k5,60≈5.000,即车辆若想通过节点7就需要付出5 km作为堵车损耗。以同样的方法确定周围节点是否发生堵车以及堵车情况如何,发现节点7周围路口均不堵车。根据堵车情况进行局部优化,此时最短路径为95 km。局部优化路径如图7所示。

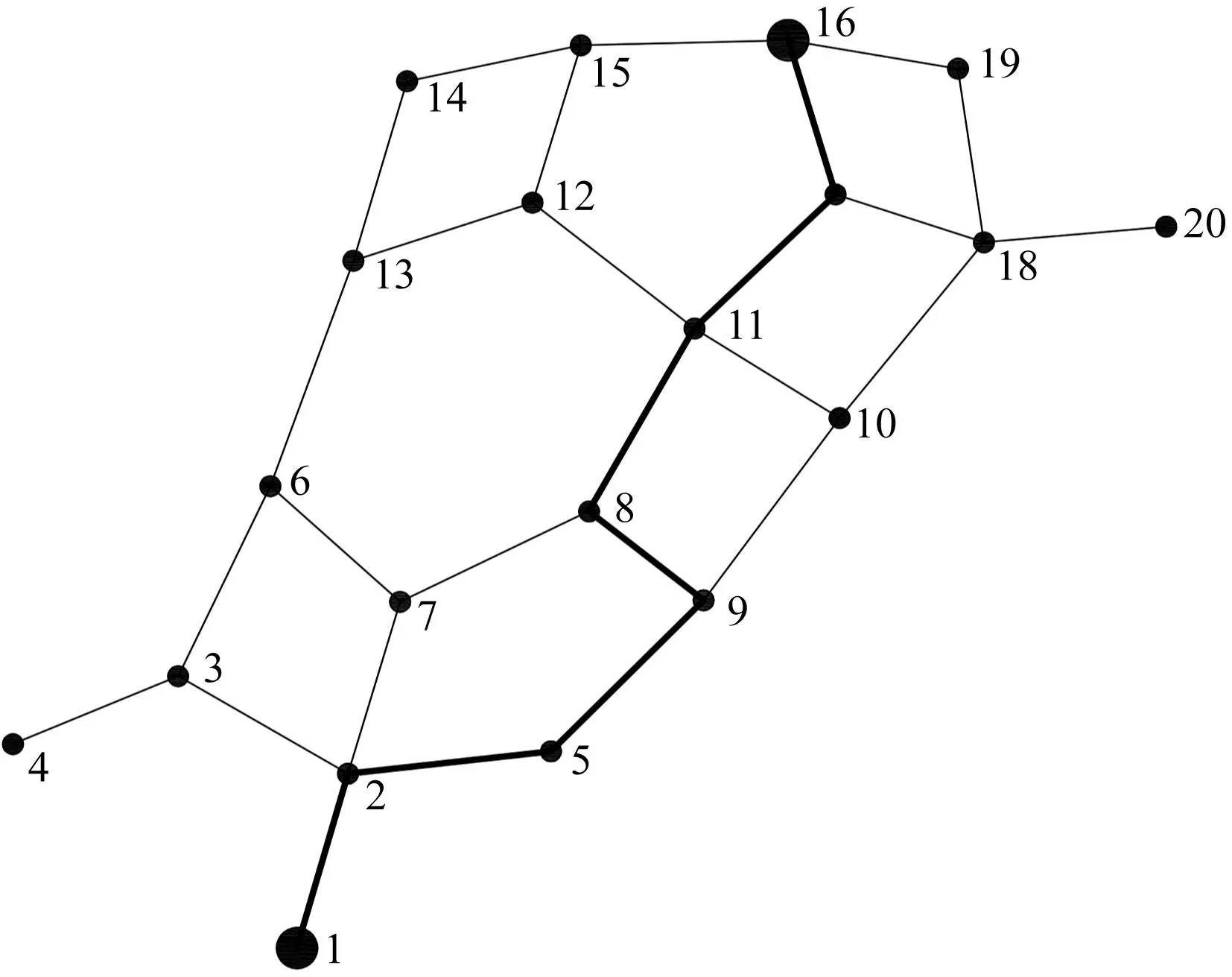
图7 局部优化路径

由于有效预测时间为75 min,但车辆在75 min内无法到达终点,因此需要在第一次75 min结束后对下一阶段路径再次进行优化,用同样的方法计算得到节点17、18会发生堵车,路车损耗分别为2.5 km、3.0 km。对第二阶段的路程进行局部优化,此时最短路径为97.0 km,车辆在有效预测时间段内到达终点,倘若不进行局部优化,仍坚持初始路径则需要98.5 km。最终路径如图8所示。

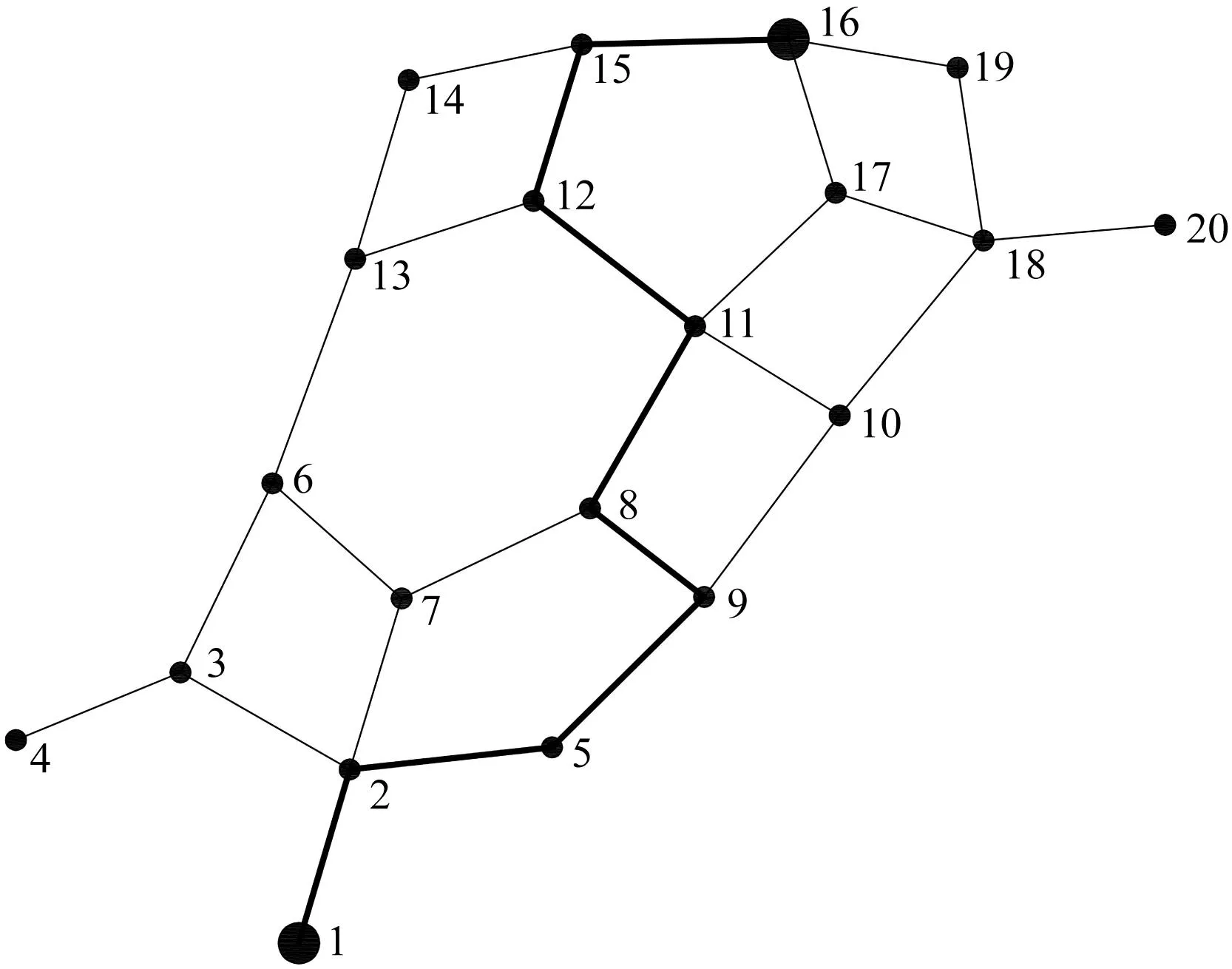
图8 最终路径

5 总结

在私家车数量越来越多、道路堵车越来越严重的情况下,目前的导航系统均基于当前道路情况进行规划,且无法对堵车信息进行量化考虑并纳入路径的规划中,导致车辆时常无法以最短的时间到达目的地。因此,本文提出一种基于预测交通流量的规划系统,使用Dijkstra算法进行全局规划的同时利用道路交通数据预测交通流量,基于道路情况选择合适的α值,判断道路是否会发生堵车及堵车程度,合理地对路径进行局部优化,减轻了堵车带来的影响。本文提出的方法具有以下优势。

(1) 基于未来道路情况进行规划,动态性能好,改善了传统规划的滞后性。

(2) 利用预测模型对未来短时交通流量进行预测并量化,将量化后的道路情况纳入路径规划中进行局部优化,从而减轻了道路拥堵给驾驶带来的影响,缩短了实际行驶距离。

(3) 可操作性强,具备一定的推广意义,还可类比应用于恶劣天气下部分交通枢纽瘫痪情况下的列车调度、节假日期间大规模出行情况下的路径规划等。

但是利用未来道路情况进行局部优化时,需要存储的道路交通数据量较大,且在某情况下,局部优化后的路径不一定是最优路径,今后可以进一步改进。