固体发动机绝热层打磨机器人的工艺参数分析①
肖 博,张志强*,王利明,周智超,肖观福,李砚徽
(1.武汉大学 动力与机械学院,武汉 430072;2.湖北三江航天江河化工科技有限公司,宜昌 444200)
0 引言
固体火箭发动机绝热层通常采用丁晴橡胶、硅橡胶等材料制备而成,其具备良好的耐油性、耐热性以及较强的粘结性等特点,能有效防止发动机壳体在高温高压等极端工况下发生损坏[1-3]。绝热层在完成固化成型工序粘贴在发动机壳体内壁后,为增加绝热层与药柱之间的粘力,需打磨绝热层表面的惰性层,打磨深度要求在0.05~0.2 mm以内,打磨均匀性要求打磨深度变化在±0.05 mm之间,以满足绝热层打磨的工艺需求。
由于橡胶材料具备高弹性、粘弹性和不可压缩性等独特的力学特征,因此表面打磨作业较为困难,目前绝热层打磨主要采用人工打磨和半自动化打磨。近年来,专用的自动化打磨机器人也陆续出现[4]。孙一兰等[5]采用工业机械臂的设计思路,设计了绝热层打磨机器人,并分析了绝热层打磨机器人的设计难点。盛强等[6-7]针对细长小口径固体发动机绝热层打磨设计了一套自动打磨设备,该设备采用长导杆结构,配合末端砂轮片进行打磨。以上设备对不同尺寸绝热层的适应性和通用性较差,且设备尺寸较大。罗学良等[8]设计了移动式打磨机器人,该设备体型小巧,可以进入燃烧室内部,自动进行打磨作业。与前两种方式相比,移动式打磨机器人使用全新的工作模式,并采用模块化设计的打磨机构和盘式铣刀进行铣削打磨作业,工作效率高,适应能力强,可满足不同尺寸绝热层的打磨需求。该打磨方式首次应用于绝热层表面打磨作业中,打磨效果受多种复杂的工艺参数影响,需明确工艺参数与打磨效果间的匹配关系。
针对上述问题,作者采用ANSYS软件,建模分析了打磨机器人新型打磨方式中各工艺参数对打磨效率和均匀性的影响,并通过实际打磨作业,验证了上述分析的可行性。本文对多刀盘打磨工艺参数分析提供了一个新思路,适用于大多数打磨工艺参数分析,能大大缩减打磨实验上的时间成本和人力成本,为后期多刀盘打磨机器人的设计、多机器人协同作业模式以及未来绝热层打磨中数字孪生在线模拟等提供设计思路和依据。
1 打磨机器人工作原理
打磨机器人整体结构如图1所示,由吸尘冷却系统、驱动转向系统、打磨系统和控制系统等组成。
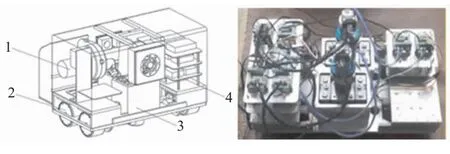
图1 打磨机器人结构图
在进行绝热层打磨作业时,驱动装置驱使绝热层壳体绕其自身中轴线匀速旋转,打磨机器人则通过其驱动转向系统自动跟随,始终保持在壳体下母线位置进行打磨,同时机器人通过差速转动,实现绝热层轴线方向上的进给运动,最终产生螺旋线状的打磨痕迹。打磨机器人打磨作业示意图如图2所示。图中,ω1为绝热层壳体旋转角速度,由驱动装置的旋转角速度ω2决定;v为打磨机器人的轴向进给速度,由驱动轮差速转动实现;D0为绝热层壳体直径。

图2 打磨作业示意图
如图3(a)所示,打磨机构由打磨电机、打磨刀盘、靠模、倾斜箱体以及导轨滑块和弹簧组成的浮动模块构成。打磨刀盘上装有若干立式铣刀片,通过刀盘转动对绝热层表面实现铣削打磨作业,如图3(b)所示。打磨刀盘与底板平面呈一定角度,且铣刀盘外侧设置有靠模,使铣刀刀刃仅高于靠模0.05~0.2 mm,可精确控制铣刀切削深度,并实现保型加工[9]。打磨装置通过导轨滑块与机器人机身连接,调节弹簧的压缩量来改变打磨下压力[10-11]。

(a)Polishing mechanism (b)Cutterhead
2 理论参数分析
为了提高作业效率,机器人采用了双刀盘作业模式,如图4所示。图4中x为双刀盘轴向间距。

图4 双刀盘排布图
采用双刀盘打磨机器人进行绝热层打磨作业,影响绝热层打磨效果和效率的参数主要有两类[12-13],其一为刀盘设计参数,涉及刀盘直径D、刀盘打磨角度θ、靠模与铣刀盘间隙d、刀刃伸出距离H、立式铣刀片切削刃圆角半径rε以及双刀盘轴向间距x等,如图5所示;其二为作业控制参数,包括燃烧室直径D0、燃烧室回转速度ω1、机器人轴向进给速度v等,如图2所示。
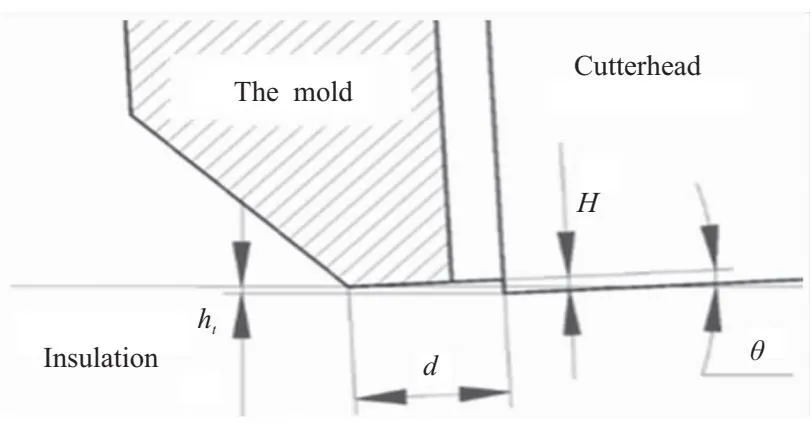
图5 打磨刀盘切削原理示意图
图5和图6分别为打磨刀盘切削原理示意图和单刀痕示意图。在不考虑绝热层回弹及下压力等因素影响下,理论切深ht可由刀刃伸出距离H、打磨角度θ、靠模与铣刀盘间隙d等参数表示:

图6 单刀痕示意图
ht=H·cos(θ)-d·sin(θ)
(1)
打磨痕迹宽度L,即刀盘旋转的轨迹与绝热层上表面相交的弦长,可直接由刀盘直径D、理论切深ht和实际打磨角度θ表示:
(2)
打磨痕迹角度β取值为(-β0,β0),β0可由刀盘直径D与打磨痕迹宽度L表示:
(3)
根据几何关系,打磨痕迹不同角度处切深h与理论切深ht、打磨角度θ以及所在打磨痕迹角度β有关:
(4)
双刀盘打磨痕迹的同圈接合状态以及螺旋进给后的异圈接合状态是影响绝热层整体打磨均匀性的重要因素。双刀盘打磨痕迹接合示意图如图7所示。为了保证绝热层整体打磨的均匀性,在打磨痕迹接合的位置要保留一定的重复度。由几何关系可知,当单圈打磨痕迹控制宽度W=2x时,异圈接合状态与同圈接合状态的重复度相同,整体均匀性较好。
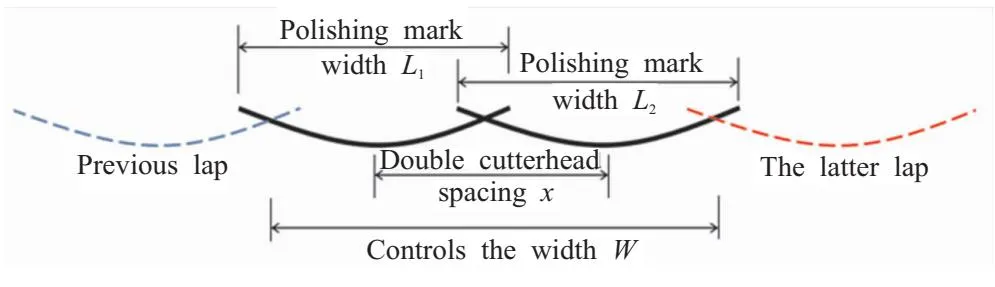
图7 双刀盘打磨痕迹接合示意图
打磨痕迹的同圈接合状态直接受双刀盘间距x的影响,为了保证打磨痕迹的均匀性,双刀盘间距x应满足以下条件:
(5)
打磨痕迹的异圈接合状态直接受双刀盘打磨机器人轴向进给宽度L0影响,L0可表示为
L0=v·t
(6)
在双刀盘轴向进给连续刀痕形成过程中,双刀盘打磨机器人轴向进给宽度L0应与单圈打磨痕迹控制宽度W等参数相匹配,即当绝热层壳体转动一圈时满足:
L0=W=2x
(7)
由此,机器人轴向进给速度v应为
(8)
机器人采用高速铣削方式对绝热层进行打磨作业,实际打磨作业时,打磨电机转速n(1000 r/min以上)远远大于燃烧室回转速度ω1(低于0.3 r/min),此高速铣削状态下,打磨电机转速n与燃烧室回转速度ω1主要通过影响每刀进给量f来影响连续打磨痕迹的均匀性。
机器人的每刀进给量f可以由燃烧室回转速度ω1、燃烧室直径D0、打磨刀盘上安装的立式铣刀片的数量a以及打磨电机转速n表示:
(9)
机器人打磨效率η可表示为
(10)
连续打磨痕迹的形貌特征与单刀痕的形貌特征、双刀盘打磨痕迹的同圈接合状态以及螺旋进给后的异圈接合状态相关,难以通过理论推导获得直观结果。
3 打磨工艺参数分析
3.1 分析模型建立
本文采用ANSYS软件对刀痕形成过程进行建模分析,直观描述出各个工艺参数对绝热层打磨均匀性的影响。由于在实际打磨工况下,燃烧室绝热层直筒段厚度只有2 mm,且刀盘下压力小于30 N,绝热层受力变形较小,且打磨深度小,回弹作用有限,因此本文所建分析模型和分析方法忽略绝热层变形和回弹的影响,即只考虑刀具回转与绝热层间几何模型干涉所引起的宏观尺度影响[14-15]。
分析模型建立流程如图8所示,首先通过ANSYS软件APDL语言,根据刀盘设计参数建立刀片回转的扇形柱体,并转动柱体至实际打磨角度,将扇形柱体沿母线向下移动距离H,模拟刀盘的实际切深。根据打磨机器人每刀进给量复制若干刀盘柱体,与绝热层体进行布尔运算获得刀片连续切深模型,最后利用SHELL181单元对切削面进行网格划分,并进行简单计算,利用ETABLE确定各单元形心位置,得到切深等值线分布图。上述模型建立时,由于机器人沿打磨痕迹主进给方向速度远远大于机器人轴向进给速度,所以连续刀痕模拟中无需考虑刀痕轴向的进给变化。

图8 分析模型建立流程
3.2 单刀盘打磨参数分析
打磨刀头通过末端立式铣刀片对绝热层进行切削,打磨效果主要受立式铣刀片切削刃圆角半径rε、每刀进给量f以及打磨角度θ的影响。
3.2.1 立式铣刀片切削刃圆角半径rε的影响
以刀具最大切深0.1 mm为控制参数,分别建立切削刃圆角半径rε为0、0.1、0.4、0.8 mm的模型进行分析,所得的单切削痕迹深度分布图如图9所示,沿打磨痕迹进给方向中心线打磨深度分布图(后文简称主进给方向深度分布)如图10所示。

(a)rε=0 mm (b)rε=0.1 mm
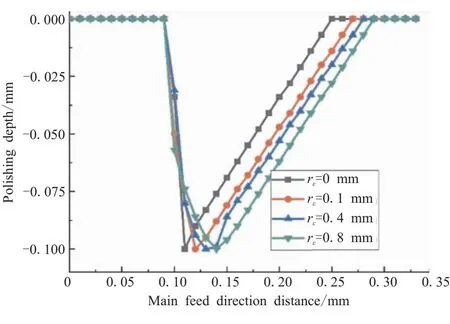
图10 主进给方向深度分布图
保持打磨角度θ=5°、单刀进给量f=0.15 mm不变,切削刃圆角rε逐渐增大时,单切痕宽度L基本保持在15 mm左右。但沿打磨痕迹中心线进给方向深度分布可知,单刀切削量逐渐增大。说明切削圆角半径越大,材料去除率越大,可以适当增加每齿进给量f,以提高打磨效率,该规律与工程实际相符。
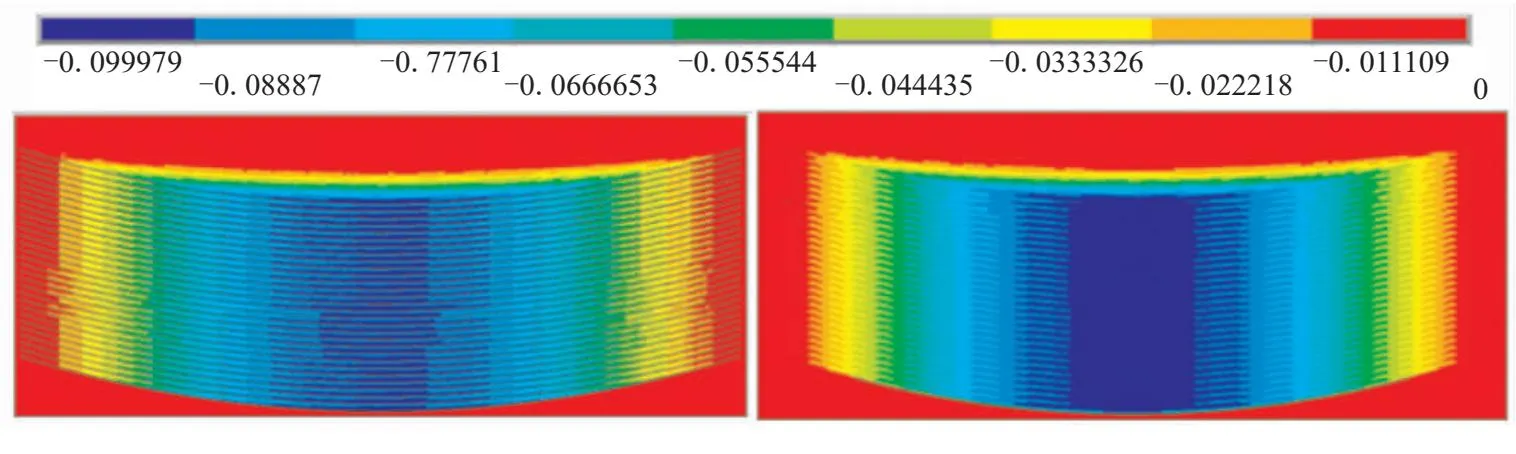
以0.1 mm切深作为控制参数,分别建立切削刃圆角半径rε为0、0.1、0.4、0.8 mm的连续切削模型进行分析,所得的连续打磨痕迹深度分布图如图11所示,沿打磨宽度方向打磨深度分布图(后文简称宽度方向深度分布)如图12所示,随着切削刃圆角变大,进给方向上刀痕的层次感逐渐消失,刀痕切宽方向上切削深度变化越来越连续,有利于绝热层打磨均匀性提高。切削刃圆角半径rε为0.1 mm和0.4 mm实际产品打磨效果如图13所示,其表面形貌与仿真模拟结果一致,说明模拟方法的合理性与有效性。当切削刃圆角提高到0.4 mm后,继续增大圆角半径,均匀性效果的提升过程趋于稳定,但电机负载会持续增加,因此工程实际中选择rε=0.4 mm的立式铣刀片。
(a)rε=0 mm (b)rε=0.1 mm

图12 切宽方向切深分布图

(a)rε=0.1 mm (b)rε=0.4 mm
3.2.2 每刀进给量f的影响
以0.1 mm切深作为控制参数,保持打磨角度θ=5°,切削刃圆角半径rε=0.4 mm等参数不变,改变刀具的每刀进给量f,模拟连续切削30次后的连续打磨痕迹,进而得到的连续打磨痕迹深度分布图如图14所示。沿打磨痕迹中心线,提取所有节点铅锤方向的坐标值,可获得主进给方向打磨深度分布情况图如图15所示。

(a)f=0.15 mm (b)f=0.25 mm (c)f=0.35 mm

图15 进给方向深度分布图
由图5可知,效率与每刀进给量f成正比,但增加进给量,打磨均匀性明显降低。当每刀进给量从0.15 mm增至0.35 mm过程中,进给方向打磨深度逐渐出现较大波动。每刀进给量f=0.35 mm时,打磨深度波动量可达到0.03 mm左右,刀痕间的层次明显增加。为了保证打磨均匀性要求,在当前打磨工艺参数下,每刀进给量f应满足f≤0.2 mm。
3.2.3 打磨角度θ的影响
仍以切深0.1 mm作为控制参数,保持切削刃圆角rε=0.4 mm,每刀进给量f=0.15 mm等参数不变,分别模拟打磨角度3°、5°、7°时的切削情况,连续打磨痕迹深度分布图如图16所示,控制参数x内宽度方向深度分布情况如图17所示。

(a)θ=3° (b)θ=5° (c) θ=7°
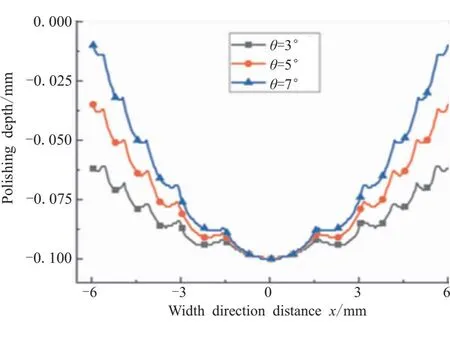
图17 打磨痕迹宽度方向打磨深度分布图
打磨角度θ由3°提高至7°过程中,刀痕宽度L由19 mm降至12.6 mm,与式(2)计算相符。以双刀盘轴向间距x作为控制参数,该参数范围内打磨深度分布直接决定双刀盘同圈打磨均匀性以及异圈接合处均匀性。由图17可知,打磨角度θ=3°时,打磨深度在0.06~0.1 mm范围内变化;打磨角度度θ=5°时,打磨深度在0.03~0.1 mm范围内变化;打磨角度度θ=7°时,打磨深度在0~0.1 mm范围内变化。表明打磨角度越小,打磨深度变化越平缓,越能保证打磨深度均匀性要求。由于绝热层内存在轴向搭接边凸起,打磨角度过小会导致搭接边表面破坏,因此经过计算,打磨角θ=5°。
3.3 双刀盘参数分析
3.3.1 双刀盘轴向间距x的影响
双刀盘打磨痕迹的同圈接合状态直接受双刀盘轴向间距x的影响。以切深0.1 mm作为控制参数,取切削刃圆角rε=0.4 mm,每刀进给量f=0.15 mm,双刀盘的打磨角度θ=5°等基本参数不变,分别模拟双刀盘轴向间距10、12、14 mm的双刀盘打磨痕迹,双刀盘打磨痕迹深度分布如图18所示。提取宽度方向打磨深度数据,绘制的宽度方向深度分布图如图19所示。

(a)x=10 mm (b)x=12 mm (c)x=14 mm
双刀盘轴向间距由x=10 mm增大至x=14 mm的过程中,打磨痕迹最大宽度Lmax由24.9 mm增大至28.9 mm,增加的长度即为双刀盘轴向间距增加值。虽然双刀盘打磨痕迹最大宽度增大,但两刀痕接合处打磨深度减小,由x=10 mm时的0.05 mm降低至x=14 mm时的0.01 mm,而且控制宽度范围内打磨深度波动量明显增大,由x=10 mm时的0.05~0.1 mm增加至x=14 mm时的0.01~0.1 mm,增加轴向间距x,虽然能在一定程度上提高打磨效率,但不利于保证打磨均匀性,因此机器人设计时取轴向间距x=12 mm。
3.3.2 机器人轴向进给宽度L0的影响
双刀盘打磨痕迹的异圈接合状态直接受螺旋线螺距的影响,螺距即机器人轴向进给宽度L0。以切深0.1 mm作为控制参数,取切削刃圆角rε=0.4 mm,每刀进给量f=0.15 mm,双刀盘的打磨角度θ=5°以及轴向间距x=12 mm等基本参数下,分别模拟轴向进给宽度L0为25 mm和30 mm的打磨痕迹,异圈接合状态痕迹图如图20所示。为了保证绝热层整体打磨均匀性,需要控制轴向进给宽度L0与双刀盘打磨痕迹Lmax相匹配。当轴向进给宽度L0大于打磨痕迹最大宽度Lmax时,多圈打磨痕迹间将出现漏打缝隙,打磨质量较差,如图20(b)所示,因此轴向进给宽度需满足L0 (a)L0=25 mm (b)L0=30 mm 以切削刃圆角rε=0.4 mm、每刀进给量f=0.15 mm、打磨角θ=5°进行单刀头打磨实验,使用光学轮廓仪扫描样品的打磨表面,获得该表面的轮廓特征如图21所示。由图21可知,被测打磨表面存在一定不均匀现象,这是由于打磨时绝热层变形以及刀头浮动造成的。整体来看打磨表面形貌与仿真切深规律一致,中间切深较深,两侧逐渐减小,表明仿真的合理性。 图21 打磨表面轮廓特征图 根据上述建模分析结果,确定了一组最佳工艺参数:切削刃圆角rε=0.4 mm、每刀进给量f=0.15 mm、双刀盘的打磨角度θ=5°、双刀盘轴向间距x=12 mm以及轴向进给宽度L0。根据这组工艺参数对实际产品进行打磨作业,打磨效果图如图22所示。由实际打磨效果可知,打磨均匀性较好,满足工艺需求。 图22 打磨效果图 本文针对设计的绝热层打磨机器人,利用ANSYS软件对打磨机器人的各个工艺参数进行模拟分析,明确了各个工艺参数对绝热层打磨均匀性的影响,分析结果表明: (1)切削刃圆角rε与打磨均匀性成正相关;每刀进给量f与打磨均匀性成负相关;打磨角度θ越大,打磨痕迹切宽越小,打磨均匀性越差;双刀盘轴向间距x越大,打磨痕迹切宽越大,但打磨均匀性越差;轴向进给宽度L0与双刀盘间距x的2倍越接近,绝热层打磨均匀性越好。 (2)打磨机器人切削刃圆角rε=0.4 mm、每刀进给量f=0.15 mm、双刀盘的打磨角度θ=5°、双刀盘轴向间距x=12 mm以及轴向进给宽度L0=24 mm时能较为高效地进行绝热层打磨,并获得很好的打磨均匀性。
3.4 机器人打磨实验
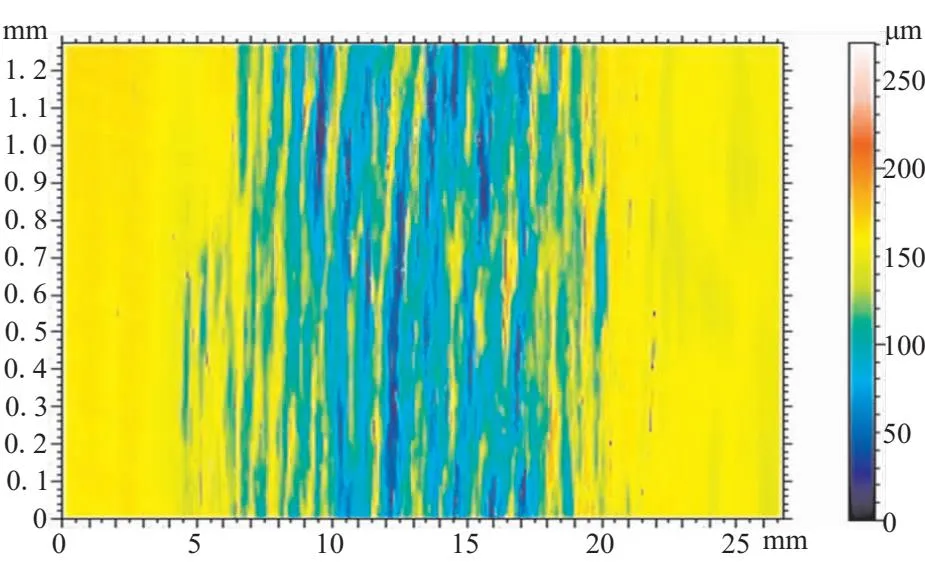

4 结论

