基于非对称泰勒综合的平面阵列低副瓣设计

赵 鹏,王 琰,刘 成

(中国电子科技集团公司第十三研究所,河北 石家庄 050200)

0 引 言

阵列综合是相控阵天线设计中的重要一环,目的是通过确定阵元的激励幅度、相位、阵元数量和位置等参数,使天线阵的远区辐射方向图满足一定的要求,如控制副瓣电平、在某处形成一定深度的零点、主瓣满足特定形状要求等[1]。理论上,进行天线阵的综合可以通过调整上述4个参数来实现,但对于一个确定的天线阵,其天线阵元数、分布形式和单元间距是确定的。本文就是考虑在确定天线阵列的情况下,通过调整阵元激励达到期望的低副瓣方向图要求。

副瓣电平成为天线性能的重要指标之一。阵元激励方法主要分为三大类:唯相位加权[2]、唯幅度加权[3]和幅度相位加权[4]。以上3种加权方法,适用于不同的应用场景。本文选择幅度相位加权,因为其比唯相位和唯幅度加权具有更大的加权自由度,但是只能工程应用于电磁波接收场景。现存主流的实现算法分为迭代算法[2]和非迭代算法[3-4]。由于迭代算法的计算时间长,本文选用非迭代的泰勒加权算法。

关于阵面的泰勒综合的研究具有悠久的历史[5]。现存的泰勒综合法有以下缺陷:应用领域限制于线阵和均匀排布的面阵[6];加权后对整个空域方向图均有影响,不能对部分空域方向图赋形;在降低副瓣的同时没有对主瓣增益下降进行约束。本文对以上问题进行了解决,并给出了明确的适用于非均匀平面阵的非对称泰勒加权公式。

1 阵列天线模型

建立侧射阵模型:

图1中平面阵列在yoz平面,阵元不一定均匀排布。其中θ是俯仰角(空域方向矢量和xoy平面的夹角),φ为方位角。

图1 侧射阵模型

根据直角坐标和极坐标转换公式:

(1)

第i个阵元和原点的光程差为:

Di=(0,yi,zi)·a

(2)

a=(x,y,z)=(cosθcosφ,cosθsinφ,sinθ)

(3)

式中:a为归一化空域方向矢量。

因此相位差为:

(4)

如果天线已经做了波束形成,并且波束指向(θ0,φ0),则该阵元得到的相位补偿为:

(5)

因此真实的相位差为:

(yicosθ0sinφ0+zisinθ0)]

(6)

因此侧射阵方向图公式为:

(7)

式中:N为阵元数;wi为阵元的加权值。

2 基于平面阵的泰勒加权方法

泰勒综合法包括幅度加权和相位加权。幅度加权由各阵元的电流激励控制,相位加权由各阵元的移相器控制。泰勒加权的核心思想是:构造一个方向图函数,使得线阵上的阵元按该函数采样后的值加权后形成的辐射方向图8和该函数相同。为线阵加权后能控制其辐射方向图的主副瓣比,该方向图函数的特性为主副瓣比可控。在计算泰勒加权值之前,先引入泰勒方向图函数。

2.1 一维对称泰勒方向图函数

根据文献[7],一维对称的泰勒方向图函数可表示为:

(8)

(9)

(10)

cosh(πA)=R0

(11)

(12)

式中:(x,A,N)为用户输入,x为函数自变量,A为该函数的主副瓣比因子,N为该函数主瓣附近等幅旁瓣个数;R0为真实主副瓣比;xn为函数所有的零点位置;ls为副瓣电平(SLL);σ为波瓣展宽因子:

(13)

考察输入对泰勒方向图函数的影响,则取对数后的泰勒方向图函数为:

F(x,A,N)=20lg(S(x,A,N))

(14)

函数特性如图2、图3所示。

图2 目标主副瓣比对方向图函数的影响

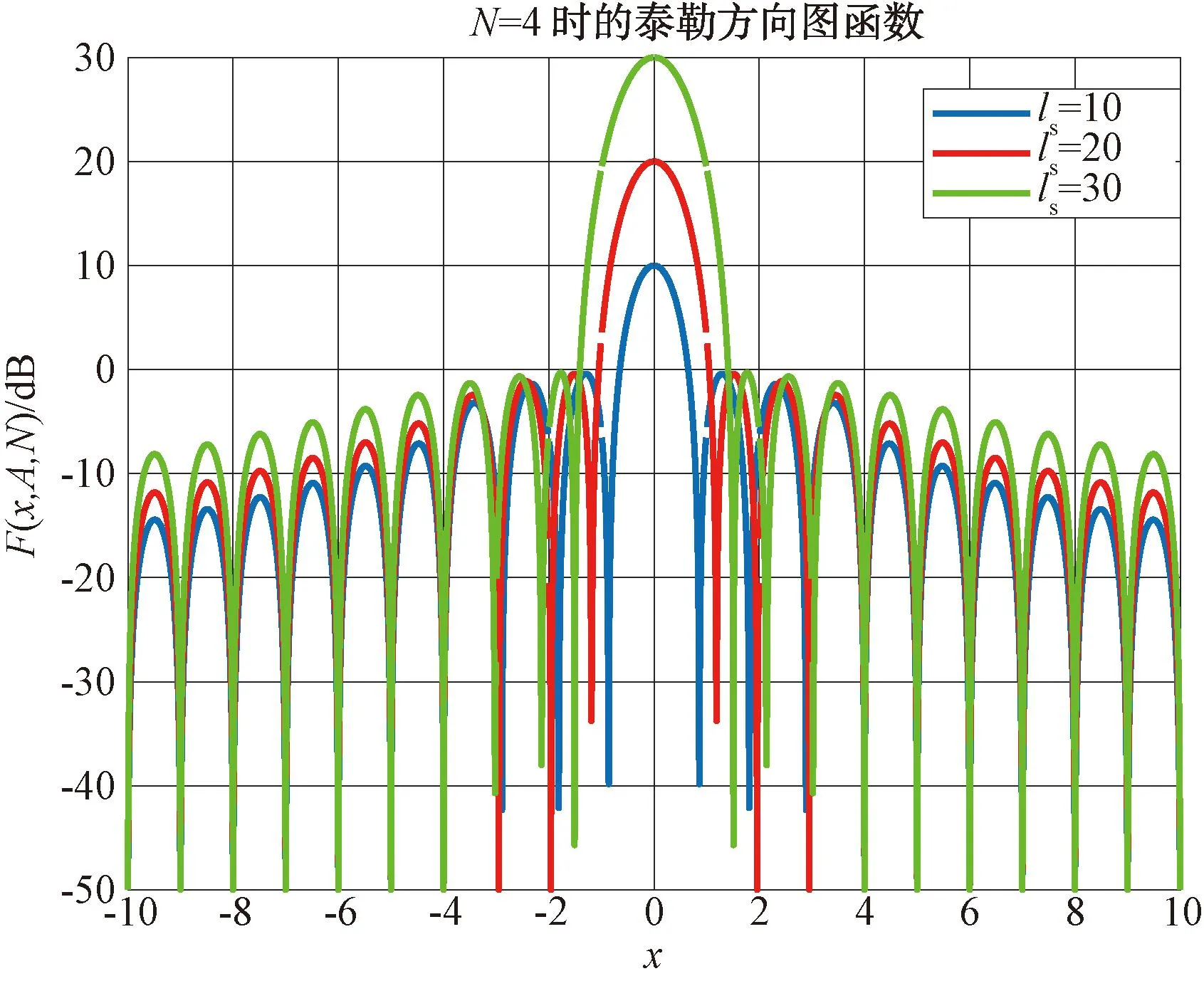
图3 等幅旁瓣个数对方向图函数的影响

函数特性满足预期的主瓣高可控、第一副瓣高为零。在工程上,幅度加权值不能超过1,并且加权值的分母不能为0,因此式(8)归一化后可以写成如下等价形式:

(15)

2.2 一维非对称泰勒方向图函数

式(8)认为方向图函数是对称的,即主瓣左右两边的副瓣高度相同,等幅副瓣个数相同,所以可以用A和N来表示主瓣两边的特征。

将式(8)推广为非对称的泰勒加权函数:

S(x,Al,Ar,Nl,Nr)=

(16)

式中:连乘不包括n=0因子;x为函数自变量;Al为该函数主瓣左侧的主副瓣比因子;Ar为该函数主瓣右侧的主副瓣比因子;Nl为主瓣左侧等幅旁瓣个数;Nr为主瓣右侧等幅旁瓣个数。

(17)

考察输入对泰勒方向图函数的影响,泰勒方向图函数取对数后为:

(18)

由图4和图5可以看出,主瓣已经发生了微小的偏移,该函数已经存在虚部。

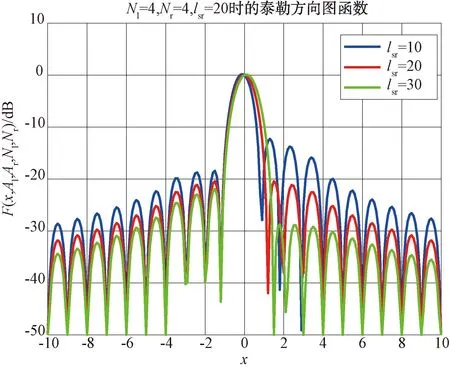
图4 非均匀泰勒方向图函数对输入的响应

图5 非均匀泰勒方向图函数虚部

2.3 二维泰勒加权值

对于非对称的泰勒方向图函数,任意线阵的阵元泰勒加权值为:

(19)

其中连加不包括x=0因子。L为单元分布的总长度,di是第i个单元的坐标值。

显然,当Al=Ar,Nl=Nr时,式(19)退化为对称的泰勒方向图对应的阵元泰勒加权值:

(20)

为方便书写,用S表示方向图函数。式(19)和式(20)的加权值具有以下性质:在给每个阵元按照式(19)加权后,产生的天线方向图可以类似于泰勒方向图函数S,即:

(21)

式中:θ为空域某角度;θ0为波束指向;F(i,θ,θ0)为第i个阵元在空域角度θ处的能量幅值函数;w(i)为该阵元的加权值。

由图3和图4可知,通过控制SLL可控制泰勒方向图函数的主副瓣比。由式(9)、(10)、(21)可知,通过控制S的主副瓣比可控制线阵方向图的主副瓣比。

对于平面阵,泰勒加权值需要对式(19)进行推广。如图1所示,对于平面阵上第i个阵元,其坐标值di包括阵面2个维度上的坐标分量yi和zi。每个分量上的加权值为:

(22)

(23)

则面阵上的阵元加权值可定义为:

wi=wiy·wiz

(24)

3 仿真实例

3.1 三角排布相控阵

阵面定义:椭圆形口径平面阵,y向宽170 mm,z向宽140 mm,共228个阵元,三角栅格排布。波束指向方位3°,俯仰5°。天线综合要求:在方位角[0°,90°]和俯仰角[-90°,0°]范围内降低副瓣,主瓣增益下降3 dB以内。图6(a)和图7(a)显示了阵面未加权时空域方向图。此时整个三维方向图主副瓣比为16.4 dBc,峰值47.16 dB。

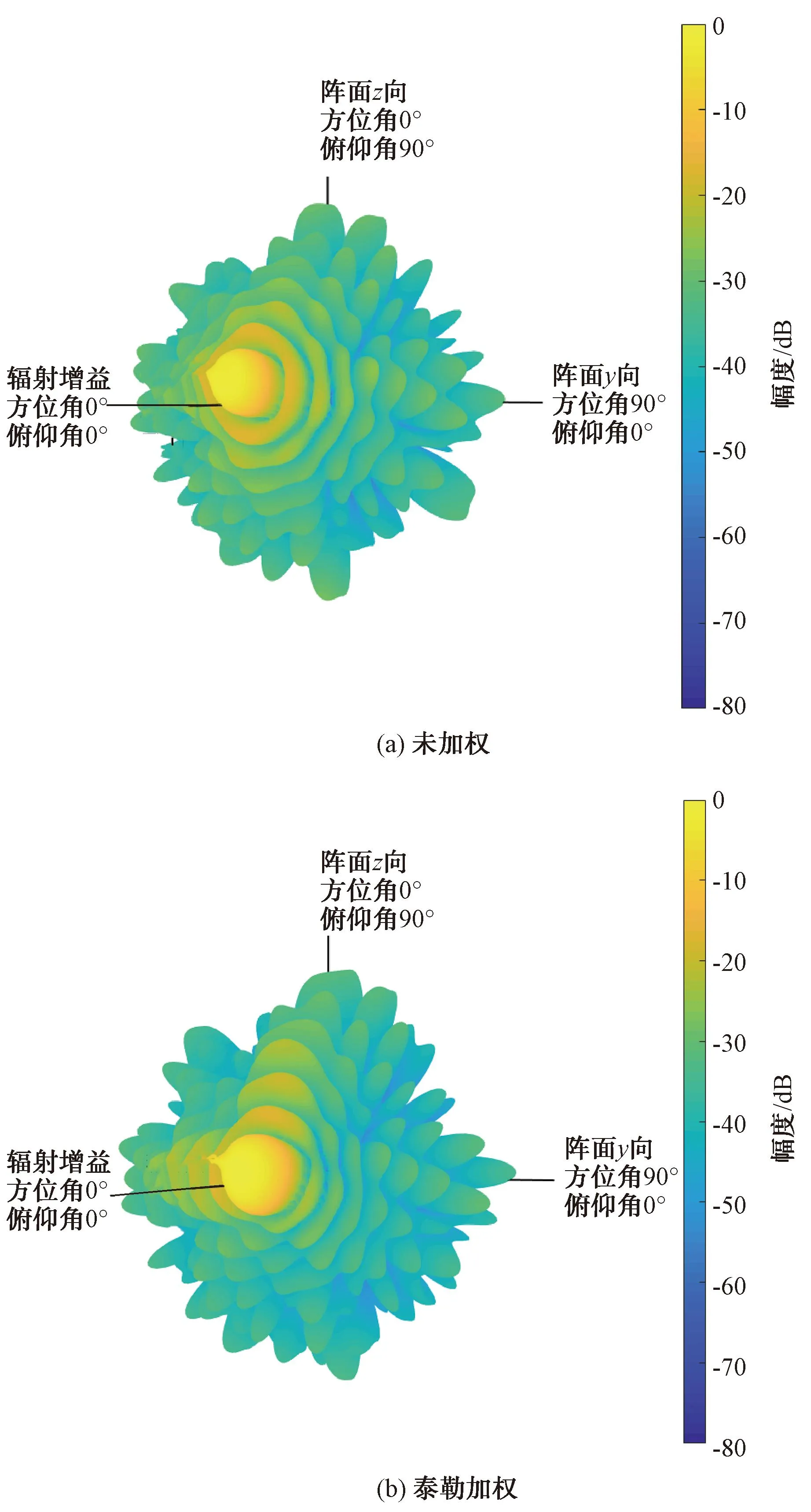
图6 阵面方向图极坐标显示

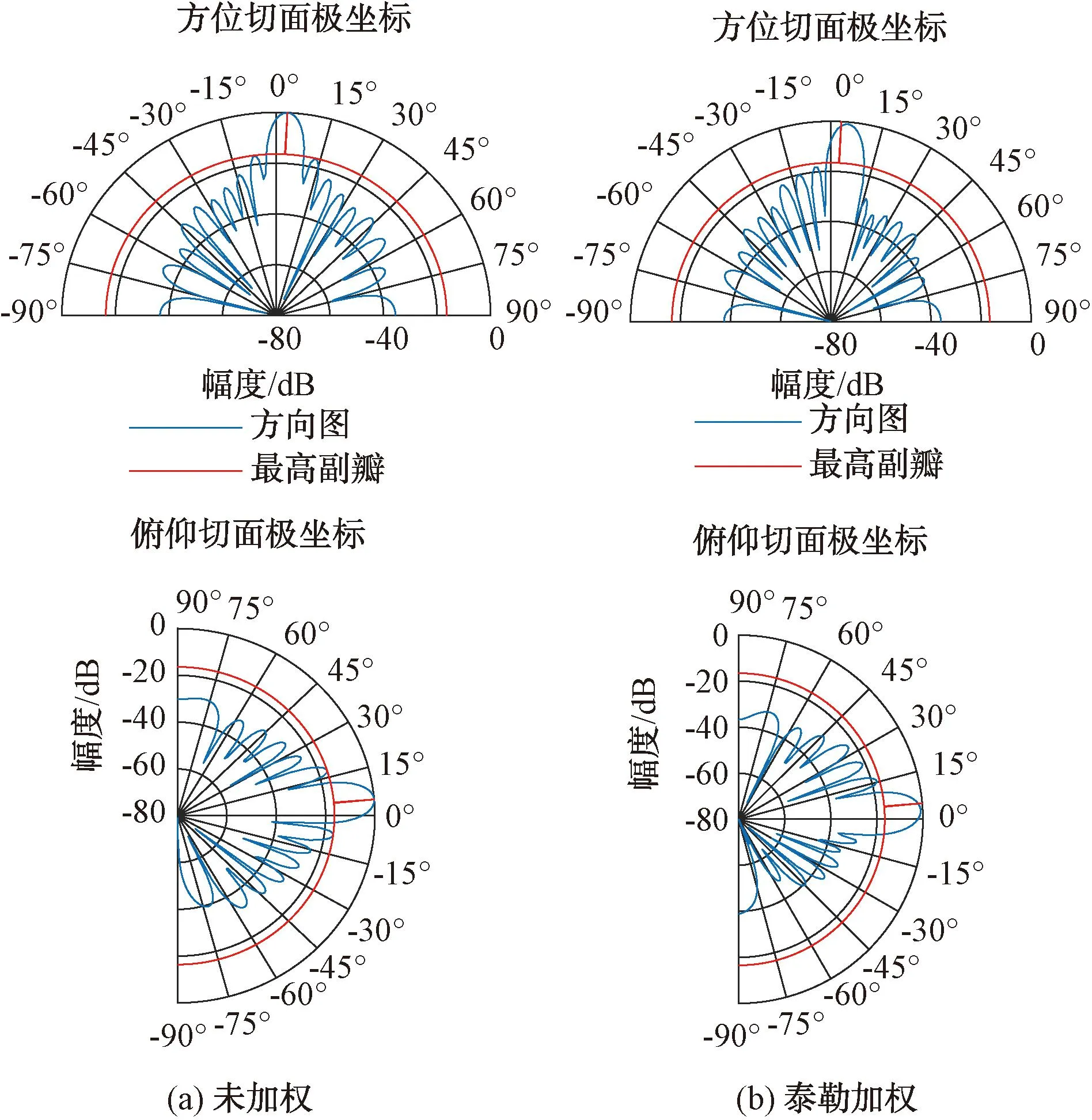
图7 阵面方向图方位和俯仰切面图显示

对整个阵面进行泰勒非对称加权,目的是在方位角[0°,90°]和俯仰角[-90°,0°]范围内降低副瓣。设置对应部分的ls=-33.8 dB(该数据由电脑依据主瓣下降限制穷举得到),其他部分的ls=-8 dB。加权后的空域方向图见图6(b)和图7(b)。加权后峰值44.17 dB,主瓣下降2.99 dB。

由图6和图7可以看到加权后方向图在方位角[0°,90°]和俯仰角[-90°,0°]范围内副瓣有明显的降低。方位切面主瓣左侧主副瓣比18 dBc,主瓣右侧主副瓣比29 dBc;俯仰切面主瓣左侧主副瓣比27.9 dBc,主瓣右侧主副瓣比7.8 dBc;整个阵面的空域方向图主副瓣比为16.6 dBc。波束指向角度有微小偏移,方位角由3°偏移到5°,俯仰角由5°偏移到3°,均向副瓣下降更多的一侧偏移。

3.2 圆形排布相控阵

阵面定义:椭圆形口径平面阵,y向宽170 mm,z向宽140 mm,共218个阵元,圆形栅格排布。波束指向方位7°,俯仰-10°。天线综合要求:在方位角[0°,90°]和俯仰角[0°,90°]范围内降低副瓣,主瓣增益下降3 dB以内。图8(a)和图9(a)显示了阵面未加权时空域方向图。此时整个三维方向图主副瓣比为16.5 dBc,峰值46.77 dB。

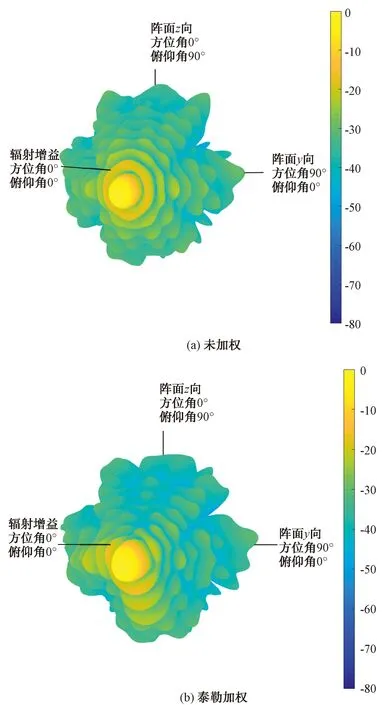
图8 阵面方向图极坐标显示

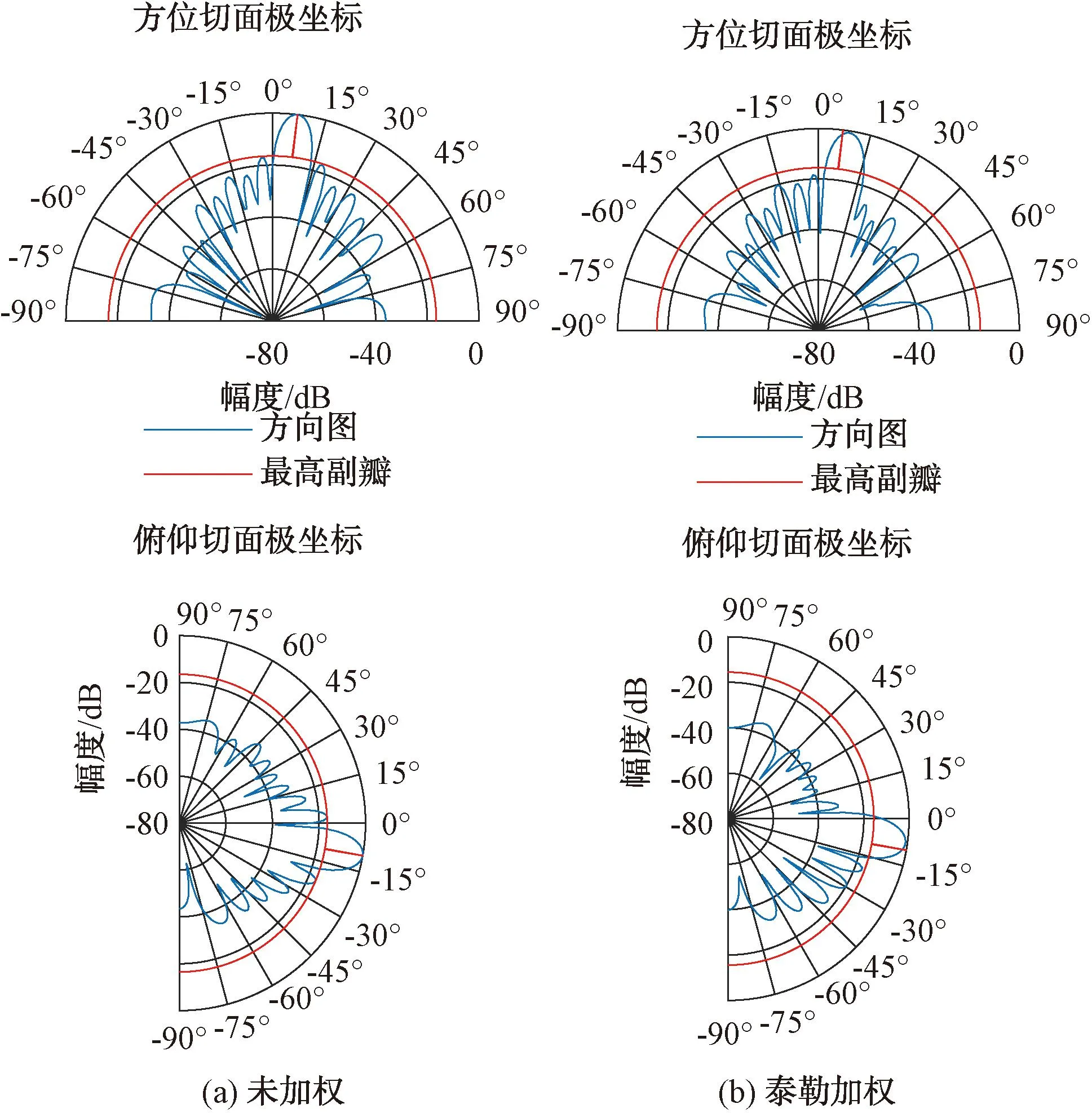
图9 阵面方向图方位和俯仰切面图显示

对整个阵面进行泰勒非对称加权,目的是在方位角[0°,90°]和俯仰角[-90°,0°]范围内降低副瓣。设置对应部分的ls=-33.1 dB(该数据由电脑依据主瓣下降限制穷举得到),其他部分的ls=-8 dB。加权后的空域方向图见图8(b)和图9(b)。加权后峰值43.79 dB,主瓣下降2.98 dB。

由图8和图9可以看到:方向图在方位角[0°,90°]和俯仰角[0°,90°]范围内副瓣明显降低。方位切面主瓣左侧主副瓣比18.4 dBc,主瓣右侧主副瓣比26.6 dBc;俯仰切面主瓣左侧主副瓣比16.8 dBc,主瓣右侧主副瓣比31 dBc;整个阵面的空域方向图主副瓣比15.7 dBc。值得注意的是,整个阵面的主副瓣比相比于加权之前的16.5 dBc变小了。指向角度有微小偏移,方位角由7°偏移到9°,俯仰角由-10°偏移到-8°,均向副瓣下降更多的一侧偏移。

4 结束语

本文给出了一种基于非对称泰勒综合的平面阵列加权方法,通过理论分析和仿真实验讨论了该方法在方向图降副瓣方面的性能。该方法具有如下优点:

(1) 适用于任意排布的平面阵列;

(2) 可对阵面方向图进行非对称的副瓣控制;

(3) 具有较小的增益损失;

(4) 加权包括幅度和相位加权,具有更大的灵活性;

(5) 算法为非迭代算法,时间成本更低。