基于多维特征模糊加权的密集目标分选关联方法

杨启伦,左 园,赵 巍,杜 冶

(中国电子科技集团公司第二十九研究所,四川 成都 610036)

0 引 言

辐射源信号分选[1-4]是电子侦察告警信号处理的关键环节,直接影响电子侦察设备性能的发挥。首先对雷达脉冲描述字(PDW)进行去交错形成分选结果,然后对多个分选结果进行关联形成目标批号,进而支撑雷达目标的威胁评估。目前学术界已有大量方法研究脉冲去交错,例如动态关联法、脉冲重复周期(PRI)直方图法、平面变换法以及基于神经网络的分选[5-8]。但是针对空中目标,由于雷达通常采用相参处理间隔(CPI)处理方式,在一个CPI内由于到达角(DOA)、射频(RF)、PRI、脉辐(PA)都一致,因此脉冲去交错并不困难,但如何将多个CPI准确关联形成目标批号目前研究较少。针对密集目标场景,由于DOA通常不可分离,导致分选结果关联错误,严重影响目标威胁评估的准确性。

模糊数学是描述、研究、处理模糊特征的数学,Zadeh提出利用隶属函数来描述模糊概念。模糊数学减少了人们对于人工经验值的确定,特别是对高维参数处理具有较好的鲁棒性。事物越复杂,人们对它的认识也就越模糊,模糊数学处理的效果就越好,目前已经广泛应用于机器人、医疗诊断、声音处理、图像处理、市场预测等多个领域[9-13]。

针对密集目标的分选关联需求,本文提出了基于多维特征模糊加权的分选关联方法,首先基于非线性欧式距离度量各维参数的隶属度,进一步通过隶属度加权实现分选结果的关联。

1 基于多维特征模糊加权的分选关联方法

基于雷达信号处理原理,雷达所使用的电磁参数跟探测性能需求相关[14-16]。在短时间内,由于探测对象、电磁环境等没有发生明显变化,因此电磁参数也存在相似性,具备一定的时域记忆特性。因此,可通过电磁参数构建高维空间作为分选结果关联的基础。

基于模糊数学理论,采用不同参数的隶属度加权术和进行关联处理,其示意图如图1所示。令第j维特征的隶属度为Pj,权重为Wj,那么高维特征的模糊加权后的隶属度为:

图1 基于模糊数学处理基础示意图

(1)

根据模糊加权后的总隶属度高低进行分选结果关联。

各维参数的隶属度可通过欧式距离来度量。当欧式距离越大,则相似度度越小,对应的隶属度也就越小。由于各维参数的量纲不同,重要性不同,以及对于雷达探测性能的作用也不同。因此对隶属度的贡献不同。在考虑测量本身存在误差的情况下,可采用非线性欧式距离,具体计算公式为:

Rnow,j=

(2)

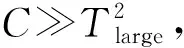
当电磁参数差异在大小门限内时,相似性采用欧式距离度量。

针对某个维度的电磁参数X,隶属度为非线性欧式距离计算倒数后再归一化处理:

(3)

即非线性欧式距离越小,则隶属度越大,同时也可看到,多个目标的隶属度之和等于1。

2 针对不同场景下中重频、高重频目标的仿真验证

为了验证本算法的性能,下面针对不同场景下中重频、高重频目标进行仿真验证。

2.1 中重频+高重频目标仿真

仿真中模拟了2部密集分布的目标,DOA测量均方差为0.3°(r.m.s),而2个目标的方差真值差异为1°,可知仅通过方位无法实现2个目标的正确分辨和关联。目标1采用中重频,重频在20～28 μs以内任意变化;目标2采用高重频,重频在10～12 μs以内任意变化。其余电磁参数范围都交叠,其中频率范围都在8 000～9 000 MHz内任意变化,脉宽范围都在2～2.6 μs,幅度都在140～210 dB范围内。2个目标交叠的CPI信息如图2所示,依据时间交叠关系,可以看到同时存在2个目标,但是难以获得准确的目标CPI关联信息。

图2 方位无法分离的中重频+高重频密集目标CPI信息

依据对于雷达目标电磁参数的经验,设置为各维度参数的门限值见表1,这里没有区分各维度参数的权重差异,统一都设置为1。基于多维特征模糊加权分选关联处理后的结果见图3。从关联后结果的时间连续性、幅度连续性等方面评估,可知2个密集目标的CPI可实现正确的关联。

表1 多维特征模糊加权分选关联算法的参数设置1

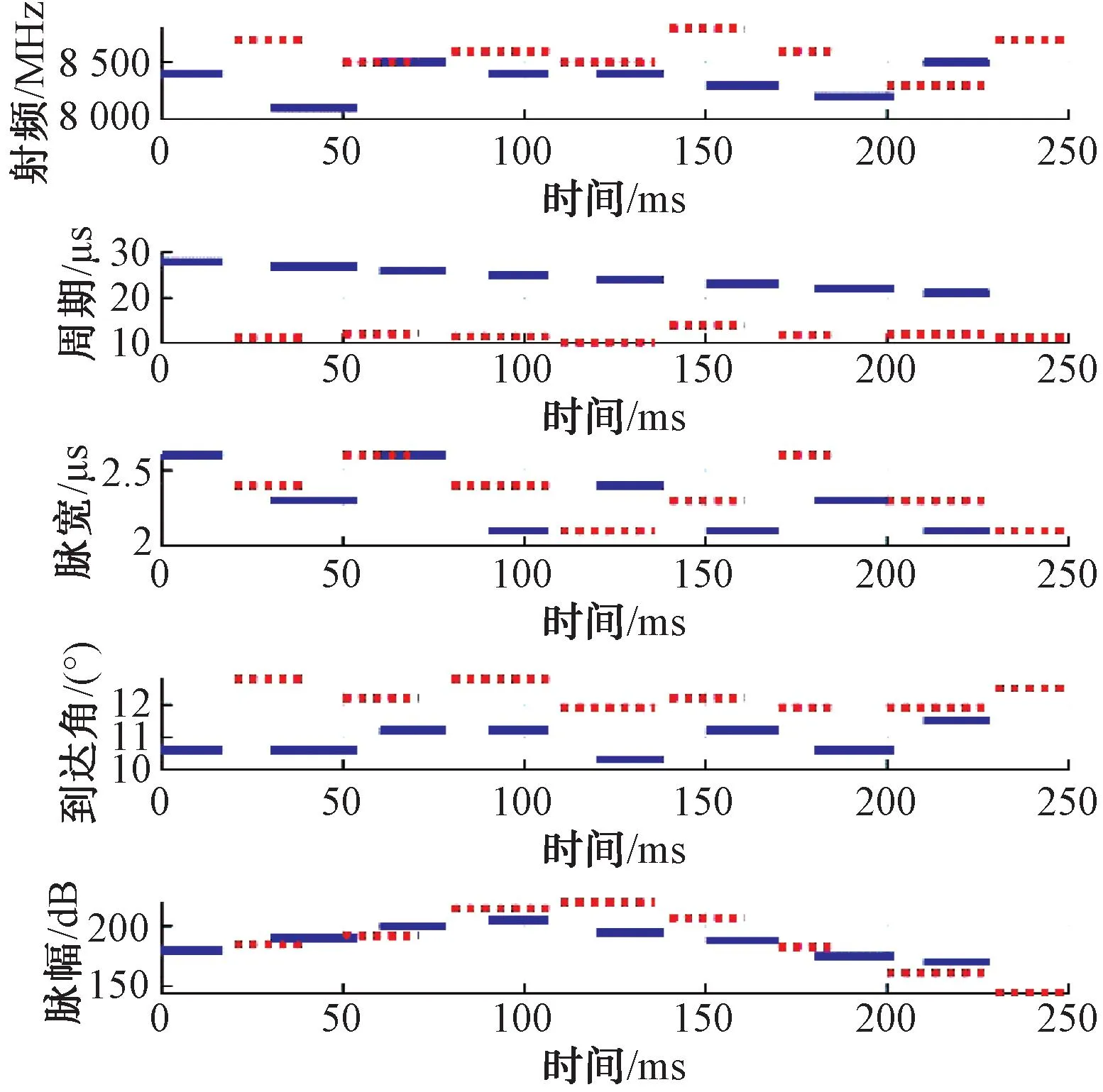
图3 基于多维特征的分选关联结果(实线为目标1,虚线为目标2)

为了验证本算法对于参数设置的不敏感性,重新设置算法参数见表2。采用基于多维特征模糊加权分选关联处理后的结果同图3完全一致。该仿真结果表明,虽然本算法需要人为设置参数,但对于算法参数的设置不敏感,具有较好的鲁棒性。

表2 多维特征模糊加权分选关联算法的参数设置2

2.2 高重频+高重频目标仿真

上述仿真中虽然密集,但仍然在PRI维度具有可分性。这里进一步仿真所有维度都无法完全分辨的情况。仿真中2个目标的频率都在9 000～10 000 MHz内任意变化,目标1和目标2都采用高重频;重频都在10～13 μs区间任意变化;脉宽范围都在1～2.5 μs区间任意变化;相对幅度都在140～210 dB范围内。2个目标交叠的CPI信息如图4所示,依据时间交叠关系,可以看到同时存在2个目标,但是难以获得准确的目标CPI关联信息。

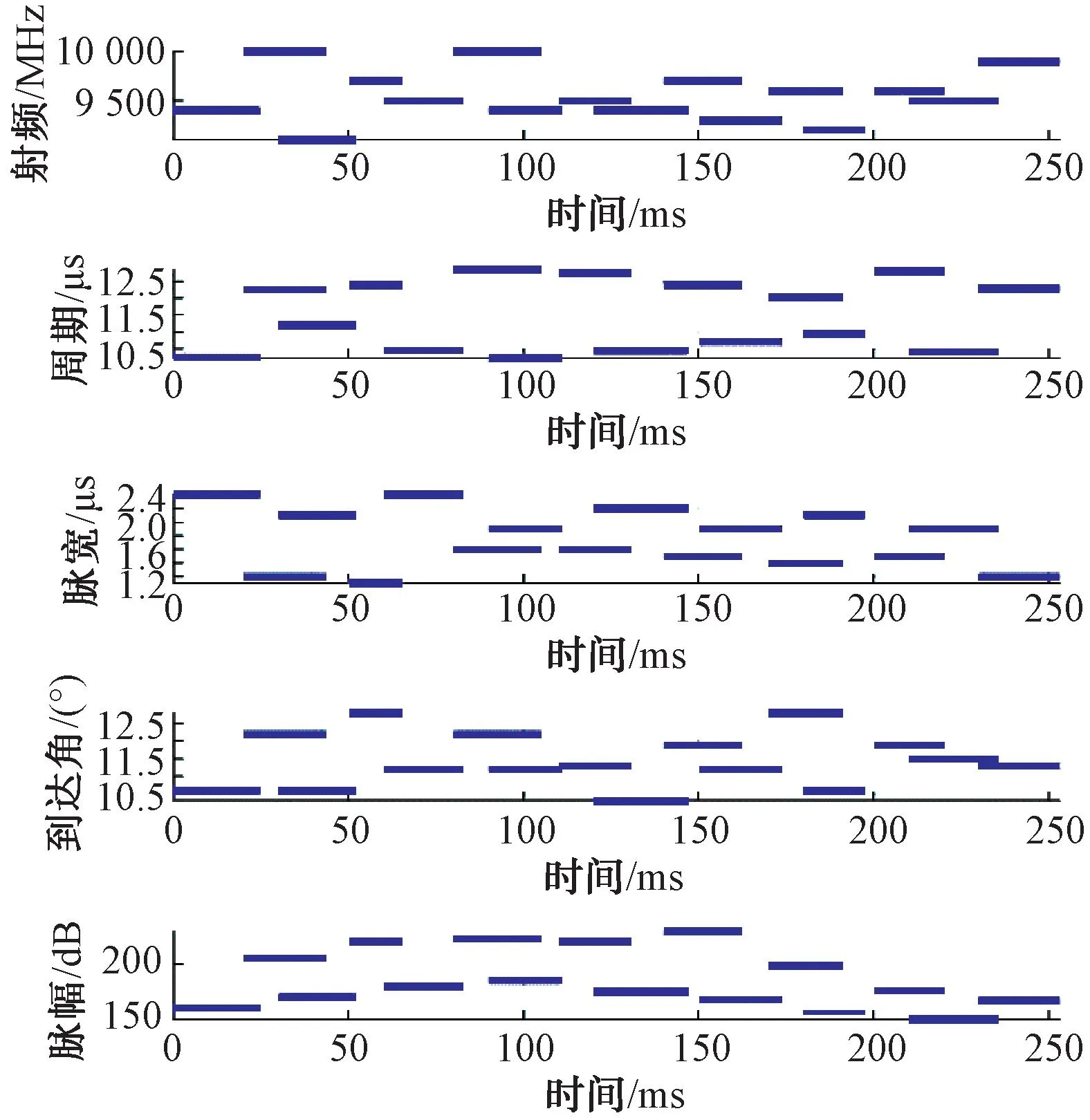
图4 方位无法分离的高重频+高重频密集目标CPI信息

分别采用表1和表2的算法参数进行仿真验证,结果都一致,见图5。每个目标CPI时间及PA的连续性结果表明,本算法针对完全交叠的电磁参数仍然具备较好的分选关联性能,同时对于算法参数不敏感,具备较好的鲁棒性。

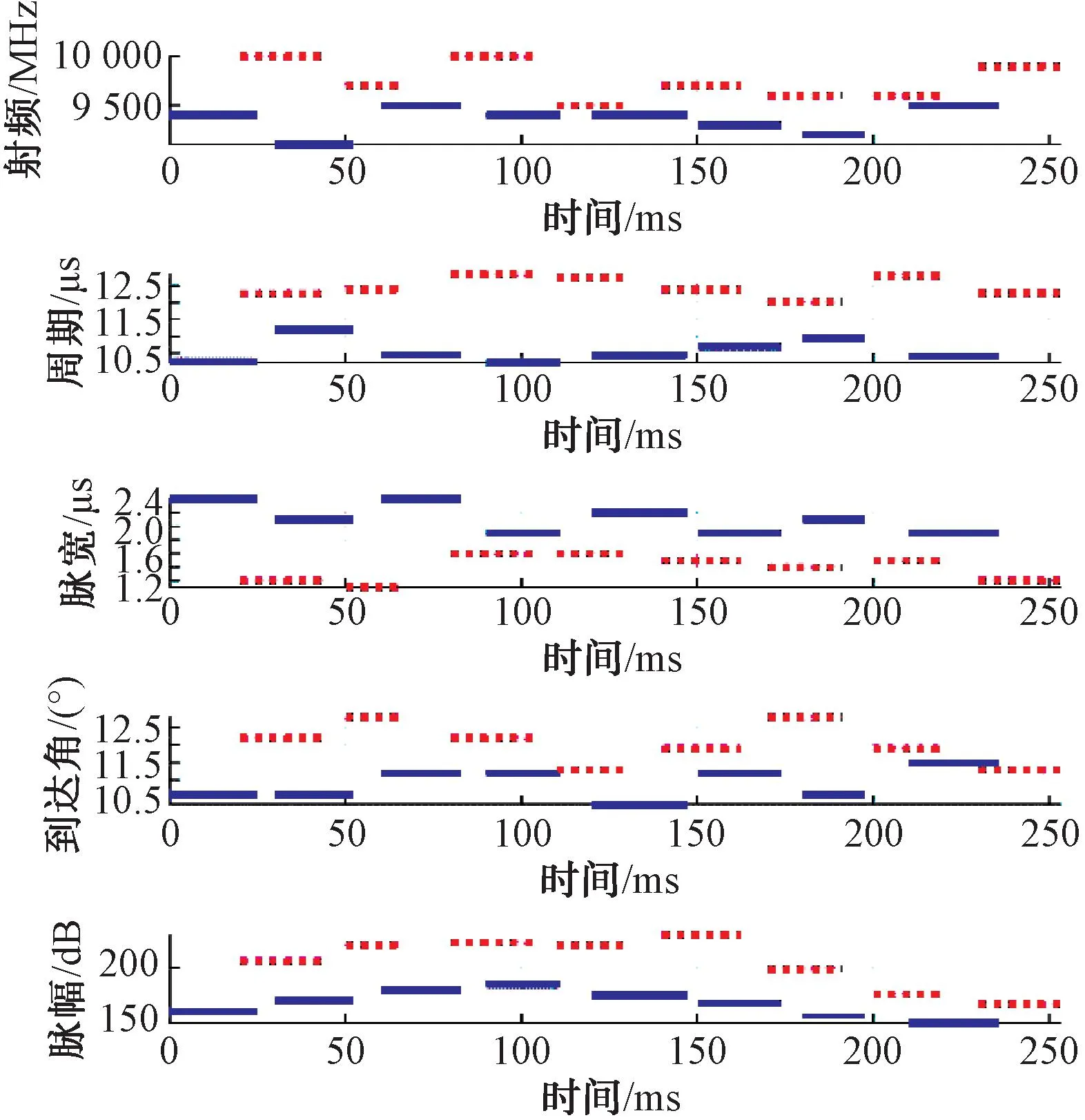
图5 基于多维特征的分选关联结果(实线为目标1,虚线为目标2)

3 结束语

针对密集目标的分选关联需求,本文基于模糊数学提出了一种基于多维特征模糊加权的分选关联方法。基于雷达探测的电磁参数在短时间内具备一定记忆性及相似性,将方位、频率、重频、脉宽、幅度等多维电磁参数,以非线性欧式距离进行隶属度度量,再结合不同参数维度的权重进行模糊加权,并基于最终的隶属度大小进行分选结果的关联。最后通过中重频、高重频等不同场景的仿真结果表明,本算法可实现参数交叠密集目标的正确关联,同时对算法参数设置不敏感,具备较好的鲁棒性。