线性回归方法在铝合金熔炼过程中的应用

朱晓毛

摘 要：铝合金材料制成的汽车零件对其机械性能有着严苛的设计要求，许多汽车零部件失效案例，如开裂，异响以及装配功能不良等早期失效，究其原因大多与硬度和机械性能不达标有关。本文列举的天窗导轨由6060铝型材制成，加工工艺有挤出、冲压、弯曲、铣削、时效（热处理）、阳极氧化以及铆接等。本文应用回归方程建模，找出熔炼过程中的铁元素的含量对于抗拉强度和断后伸长率的对应关系，对回归方程的显着性进行检验，通过解一组不等式来确定“铁（Fe）”元素的含量，从而指导实际熔炼过程中的控制和预测。

关键词：铝合金 线性回归 质量控制

1 引言

铁（Fe）元素如果过量对于铝合金而言是具有危害作用的，杂质的铁（Fe）会生成Fe3Al2的针状结晶，形成硬点，降低铝合金规定非比例伸长应力和对应的伸长率，因此需要精细和严格控制。当含铁（Fe）量超过1.2 %时，会降低合金流动性，如缺料，壁厚不均，损害挤出件的品质，如拉伸开裂，变形，另外还会缩短挤出设备中金属组件的寿命，如顶杆，柱塞，另外将加速挤出模的磨损。大多数铝合金中，铁（Fe）元素都属于受控制的杂质，有铁（Fe）元素的存在，通常会降低合金的塑性性能，对断裂韧度有负面影响，影响压力加工和铸造性能。失效模式见图1。

天窗导轨变形、开裂，弧度不良，尺寸稳定性等问题是天窗开发过程中经常遇到的顽疾，其开发涉及多个工艺技术，需满足多种匹配方案，具有特殊性、复杂性。现有多种工艺技术新的方法还在源源不断应用，需比较/分析各种方法的特点，探索科学高效的导轨制造和质量控制处理思路，设计具有性能良好，较高经济的参数方案，已成为设计、项目、质量和管理等部门亟待解决的问题。导轨工艺方法选择不合理、熔炼配比设计不科学、热处理工艺控制不精确，质量管理不到位等问题，将影响天窗总成质量、项目周期及成本，也有可能延期整车发布和危害公众生命安全。需要深入研究国内外天窗导轨控制经验和相关研究成果，提升质量能力。

2 熔炼数据整理

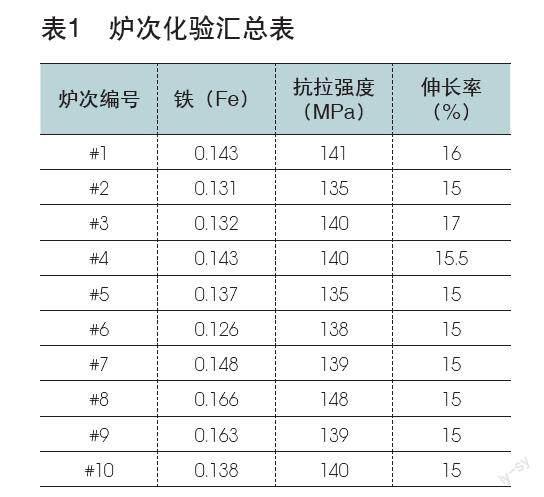
首先，收集铝型材供应商不同炉次的铝水化验结果，剔除异常数据后，整理得出以下数据，见表1。

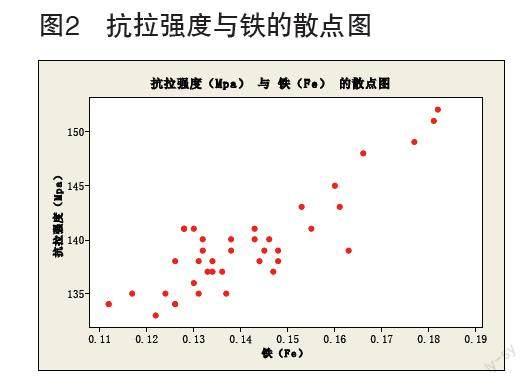
描述两个变量之间关系的模型，首先想到的是一元回归分析，两个变量之间的线性相关关系是其研究的主要对象。结合本案例，以铁（Fe）含量作为横坐标，以抗拉强度（MPa）作为纵坐标，将这些数据标在一个坐标系中，以散点图的形式展现，则可得图2和图3。

从两幅图中可以大致看出，数据点基本落在一条直线附近，能够初步判断出自变量X与应变量Y呈现某种线性回归关系。从图中还可以看出，并非所有的数据点都完全落在一条直线上，因此X与Y的关系并没有确切到可以唯一地由一个X值确定一个Y值的程度，其它因素，诸如其它微量元素（如锰、鉻、镍、锌等）的含量以及试验误差、测量误差、记录误差等因素均会影响Y的结果，要进一步研究X与Y的关系，则必须使用线性拟合方法。

3 建立含铁量与抗拉强度回归关系

上述数据分析后，开始尝试建立回归模型，为分析抗拉强度和伸长率这两项指标与含铁（Fe）量之间的关系，建立三者之间相互关系的回归模型，设Y1，Y2分别为该6060铝合金的抗拉强度和伸长率，X为含铁量，则：

Y1=β01+β1X+ε1

Y2=β02+β2X+ε2

Y与X之间的关系可以用两个方面表述，一个方面是由于X的变化引起Y线性变化的部分，即β01+β1X；另一方面是由其他所有随机因素引起的，记为ε。上述两式是变量Y对X的一元线性理论回归方程。通常情况下Y被称为因变量，X为自变量。其中β01和β1是位置参数，称β01为回归常数，β1是回归系数。Ε表示其他随机因素的总体影响，是一个随机变量，通常假设ε满足E（ε）=0，主要含义是数学期望，Var（ε）表示ε的方差，通过两端求期望，得到公式E（Y）=Y1=β01+β1X1。

为了由样本数据得到回归参数β01和β1的理想估计值，通常情况下会运用到最小二乘估计（Ordinary Least Square Estimation， OLSE），即对每个样本值（Xi，Yi）进行考虑观测值Yi与其回归值E（Yi）=β01+β1Xi的离差越小越好，综合地考虑n个离差值，定义离差平方和：

所谓最小二乘法，就是选择Xi和Yi使Q（Xi，Yi）最小，寻找参数β01，β1的估计值β^0，β^1，使公式定义的离差平方和达到极小，即寻找β^0，β^1，满足：

按照微积分知识要求，可以得知，要想使公式取得最小值，必须满足以下两个条件：

进一步将公式加以简化得到以下正态方程组：

通过以上计算，即可得到回归系数的最小二乘估计，在知道了回归斜率系数的估计值后，可以采用截距系数的估计值公式来手动计算出它的数值。需要注意的是，最小二乘估计值并不是“最佳估计”的唯一方法和准则。此处采用是由于这种方法公式较为简单，计算方便，得到的回归系数b0和b1具有更好的统计性质（指残差和总是等于零，或者说误差的样本均值为零。无论样本的散点图分布如何，最小二乘法拟合的回归线总是穿过散点的质心），线性、无偏性和有效性。

利用上述公式，逐步计算回归方程的各个参数。首先抗拉强度与铁含量之间的回归方程，计算得：

x-=5.619/40=0.140475，y-=5574/40=139.35

=0.801043-40×（0.140475）2=0.012103975

=785.665-40×0.140475×139.35=2.65735

带入下式

β^1=Lxy/Lxx=2.65735/0.012103975=226.85

β^0=y--β^1x-=139.35–（226.85×0.140475）=107.48

于是得到抗拉强度与铁含量的回归方程为

Y1=107.48+226.85X1

Minitab进行了复核，会话窗口输出结果见图4。

回归分析：抗拉强度（MPa）与铁（Fe）

回归方程为：

抗拉强度（MPa）=107+227铁（Fe）

从计算机输出结果中可以得出，自变量列中的两个值即为β^0=107.48，β^1=226.85，这与手工计算结果是一致的。得到此问题的经验回归方程后，还不能马上就用它去做分析和预测，因为还未充分确定Y1=β01+β1X1是否真正描述了变量Y与X之间的统计规律性。

对于判断是否拒绝原假设，我们利用t分布和软件计算出来的t统计量的值，计算概率P（︱t︱＞︱t值︱），此处的概率值被称为P值，即P（︱t︱＞︱t值︱）=P值。根据t分布的性质可知：︱t值︱越大，P值越小；︱t值︱越小，则P值越大。因此对于给定的显著性水平a，每当P值＜a时，应该拒绝原假设；每当P值＞a时，则不应该拒绝原假设。在给定显著性水平的情况下，使用P值不需要查分布表就可以做出判断是否拒绝原假设。

另外，β^0的标准差=3.061，β^1的标准差=21.63，t=10.49，取显著水平a=0.05，自由度n-2=40-2=38，查t分布表得临界值t（a/2） =1.686，由︱t︱=3.061＞ 1.686可知，应拒绝原假设H0：β1=0，认为抗拉强度与铁含量的一元线性回归方程：Y1=107.48+226.85X1的效果显著。

4 建立铁含量与伸长率之间回归关系

同理，根据最小二乘法的估计算法，重复上述步骤，可以得出伸长率与铁（Fe）的回归方程，Minitab会话窗口所得参数如下：

回归分析：伸长率（%）与铁（Fe）

回归方程为：

伸长率（%）=20.8-39.0铁（Fe）

建立伸长率与铁含量的经验回归方程为

Y2=20.8–39X2

残差见图5。另外得到β^02的标准差为0.6924，β^2的标准差是4.893，t值为-7.96，同样取显著水平a=0.05，自由度为n-2=40-2=38，查t分布表临界值t（a/2）=1.686，由︱t︱=7.96＞2.101可知，应拒绝原假设 H0：β1=0，认为伸长率与铁含量的一元线性回归的效果显著。

5 计算铁含量的控制范围

由于所得到的两个回归方程都是高度显著的，因此能够应用于实际生产控制，由本案例所给出的质量控制要求，抗拉强度Y1应大于120 MPa，伸长率Y2应大于14%，对两个指标均是单侧控制要求（无上限设置），即要求含铁量X的控制范围，使以下两个公式同时满足要求

P（Y^1–D1＞120）=0.995

P（Y^2–D2＞14）=0.995

样本容量N=40，较大，因此可用近似公式求解D1和D2，a=0.01，ta（N-2）=t0.01（38）在t分布表中查临界值，得t0.01（38）=2.4286，于是：

D1=t0.01=2.4286×3.061=7.43

D2=t0.01=2.4286×0.6924=1.68

得以下不等式组：

107.48+226.85X–7.43＞120

20.8–39X-1.68＞14

解此不等式组，得：0.088＜X＜0.132。由此得知，只要在铝合金熔炼过程中将含铁（Fe）控制在0.088%～0.132%之间，就可以有百分之九十九的把握使该铝合金型材的抗拉强度大于120MPa，伸长率大于14%。

6 结论

本文介绍了线性回归方程这一数学工具应用于实际生产的案列，收集了不同炉次的化验数据，剔除异常，简析熔炼方法和成分配比，明确了铁元素（Fe）对于抗拉强度和伸长率之间的回归关系，运用最小二乘法，建立了铁元素（Fe）与这两者之间的线性回归方程，得到回归参数β01和β1的理想估计值，采用截距系数的估计值公式来手动计算出它的数值，分别进行残差分析，最终得出线性回归效果显著，故可用于日常生产控制，通过解不等式组，得出铁元素（Fe）含量的控制范围，很好地指导了过程质量控制。

参考文献：

[1]马林，何桢.六西格玛管理 第二版[M].中国人民大学出版社，75-82.

[2]劉胜新.实用金属材料手册[M].机械工业出版社出版，2011.

[3]何晓群，刘文卿.应用回归分析[M].中国人民大学出版社，2001.

[4][美]，诺尔曼E.道林.工程材料力学行为——变形、断裂与疲劳的工程方法，中文版[M].原书第4版.机械工业出版社.2016.

[5]张建同.实用多远统计分析[M].同济大学出版社，2016，10-18.

[6]谢宇.回归分析（修订版）[M].社会科学文献出版社，2013.

[7]马逢时，吴诚鸥.基于MINITAB的现代实用统计[M].中国人民大学出版社，2009.

[8]金光.数据分析与建模方法[M].国方工业出版社，2013.

[9]闵亚能.实验设计（DOE）应用指南[M].机械工业出版社，2011.