高温作用下植筋套筒拉拔性能的有限元分析
孟晓阳,唐兴荣
(苏州科技大学土木工程学院,江苏 苏州 215011)
0 引言
植筋技术广泛应用于建筑结构的加固改造领域,国内外学者对常温下植筋锚固性能进行了较为完整的试验研究和理论分析[1-11],已得到大量常温下植筋锚固性能的研究成果,促进了后植筋锚固技术的广泛应用。在实际工程中,植筋锚固构件也可能会受到火灾(高温)等的影响,高温时植筋胶的黏结性能会明显降低,导致植筋锚固性能退化甚至失效。目前,国内外学者[12-16]对高温作用下植筋锚固性能的研究不多,因此,进一步开展高温作用下植筋套筒试件的拉拔性能的研究有现实意义。本文采用Abaqus有限元软件,以受热温度、植筋锚固长度等为参数,对高温作用下的植筋套筒拉拔性能进行模拟分析,为高温下后植筋锚固技术提供技术支撑。
1 有限元模型的建立
1.1 材料本构关系
1.1.1 钢材的应力-应变本构关系
根据《混凝土结构加固技术规范》(GB 50367—2013)[17]附录C中的钢套筒要求,套筒材料为45号碳素钢,植筋采用HRB400级钢筋。温度作用下套筒、植筋的应力-应变本构关系选用文献[18]提出的温度作用下钢材的本构关系(见图1),即:
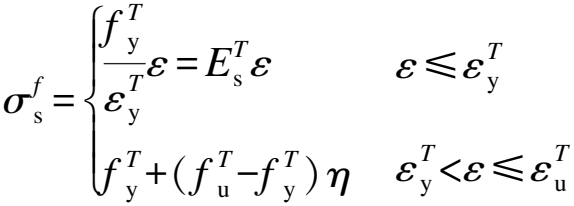
(1)
η=(1.5ξ-0.5ξ3)0.62
(2)
强化段曲线所取的相对坐标(ξ,η)按式(3)计算,
(3)
(4)
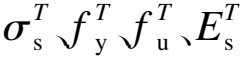
(5)
(6)
(7)
fy、fu、Es分别为常温下钢材的屈服强度、极限强度及弹性模量。
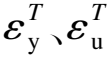
(8)
(9)
1.1.2 胶-筋界面黏结-滑移本构关系
有限元模拟试件与文献[14]钢套筒拉拔试件采用的植筋胶均为FISV360S。高温下胶-筋界面黏结-滑移本构关系采用文献[14]通过高温套筒试验得到的不同温度下胶-筋界面黏结-滑移本构关系,即:
(10)
式中:a、b为系数,取a=1,b=0.5;τ0、S0分别为不同温度下植筋胶黏结-滑移曲线最大黏结应力及其对应的滑移量,按表1取值。

表1 不同温度时最大黏结应力及其对应的滑移量
1.2 单元的类型
不同温度作用下的植筋、套筒均采用八节点六面体单元C3D8R。植筋与套筒之间黏结作用采用Spring2弹簧单元进行模拟。
1.3 网格的划分
钢筋与胶层部件接触部分是整个植筋体系受力最复杂的地方,在网格划分时,钢筋埋深范围内的网格划分要相对密集。因为胶-筋界面之间的黏结作用使用非线性弹簧定义,所以套筒和钢筋这两个实体单元在埋深范围内布种的密度应该相同,本文采用按边布种的方法,套筒和钢筋单元沿埋深方向布置12个局部种子,在钢筋周长与套筒内径周长上布置16个局部种子,每个钢筋和套筒单元的长度为 3 mm。以此保证两者单元大小相等,使钢筋单元和套筒单元的相应节点重合。各部件网络划分如图2所示。
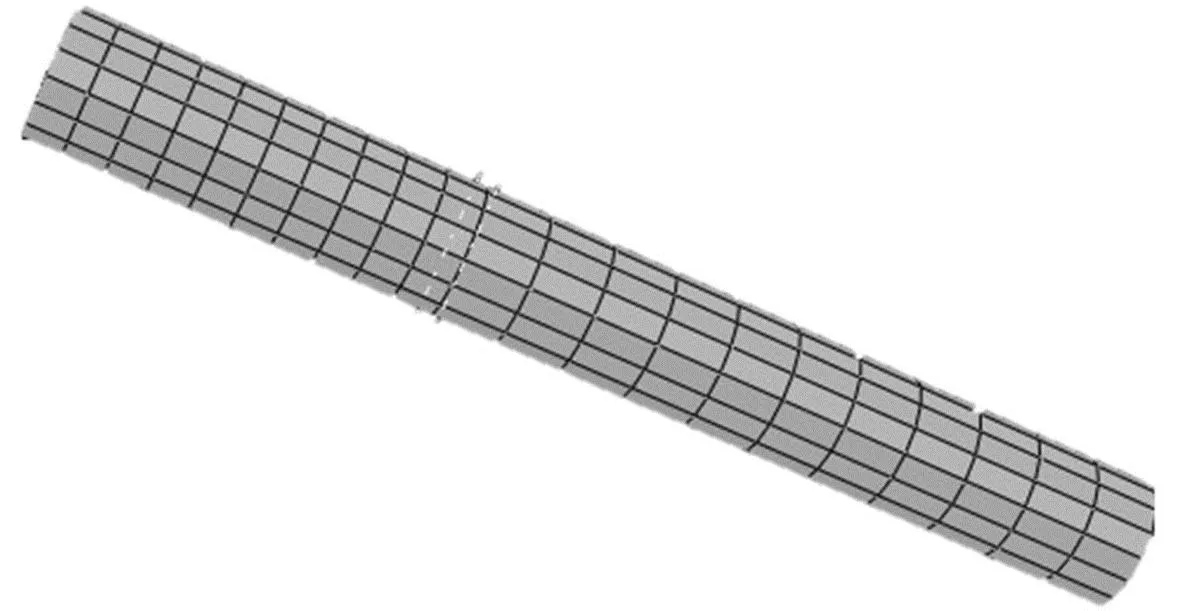
(a)钢筋
1.4 交界面上黏结应力的定义
钢筋与套筒间的黏结采用Spring2弹簧单元进行模拟。Spring2非线性弹簧单元定义了节点之间的荷载和滑移(P-S)之间的关系。根据各界面不同的黏结-滑移本构关系确定P-S关系曲线。Spring2非线性弹簧是有3个方向的作用单元。本模拟z方向为切向弹簧,是模拟黏结力和位移关系的非线性弹簧。x和y方向为法向弹簧。本次模拟只考虑z方向上的拉伸,x和y两个方向不施加荷载,x和y方向的弹簧刚度为无限大,忽略x和y方向的相对滑移,输入一个较大的数字即可,参考已有文献[7—11],本模型弹簧刚度选用大于植筋胶弹性模量数量级的一个数值,将x、y方向的弹簧刚度设为7 800 000 N/mm。
弹簧P-S的数学表达式如下:
P=τ(S,xi)×Ai
(11)
(12)
式中:τ(S,xi)为界面滑移S下相对埋深x处的黏结应力;i为弹簧单元个数;Ai为单个弹簧的控制面积;D为交界面直径,即植筋钢筋直径;la为植筋黏结长度;n为控制面积内的弹簧个数。
通过布置非线性弹簧的方式,可以将胶-筋界面的黏结-滑移规律转化为弹簧力与弹簧拉伸长度。在Abaqus中仅能设置线性弹簧,由于胶-筋界面的黏结-滑移本构关系为非线性,因此,需要对INP文件进行编写,以完成非线性弹簧单元的设置。在INP文件编写过程中,黏结-滑移本构关系定义的力与相对位移值必须按照升序排列,否则有限元模型运行过程中会出现错误。
2 有限元模型可行性的验证
为了验证上述有限元模型的可行性,对文献[14]中钢套筒高温下拉拔试验进行模拟分析。套筒材料为45号碳素钢,其屈服强度fy=439 MPa,极限强度fu=647 MPa,弹性模量Es=2.1×105N/mm2,泊松比υ=0.3;植筋采用HRB400级,其屈服强度fy=415 MPa,极限强度fu=640 MPa,弹性模量Es=2.1×105N/mm2,泊松比υ=0.3。套筒外径40 mm,植筋端内径16 mm,植筋深度36 mm,螺杆端内径24 mm,螺纹长度24 mm。不同温度下试件的荷载-滑移(P-S)曲线模拟值与试验值比较如图3所示。
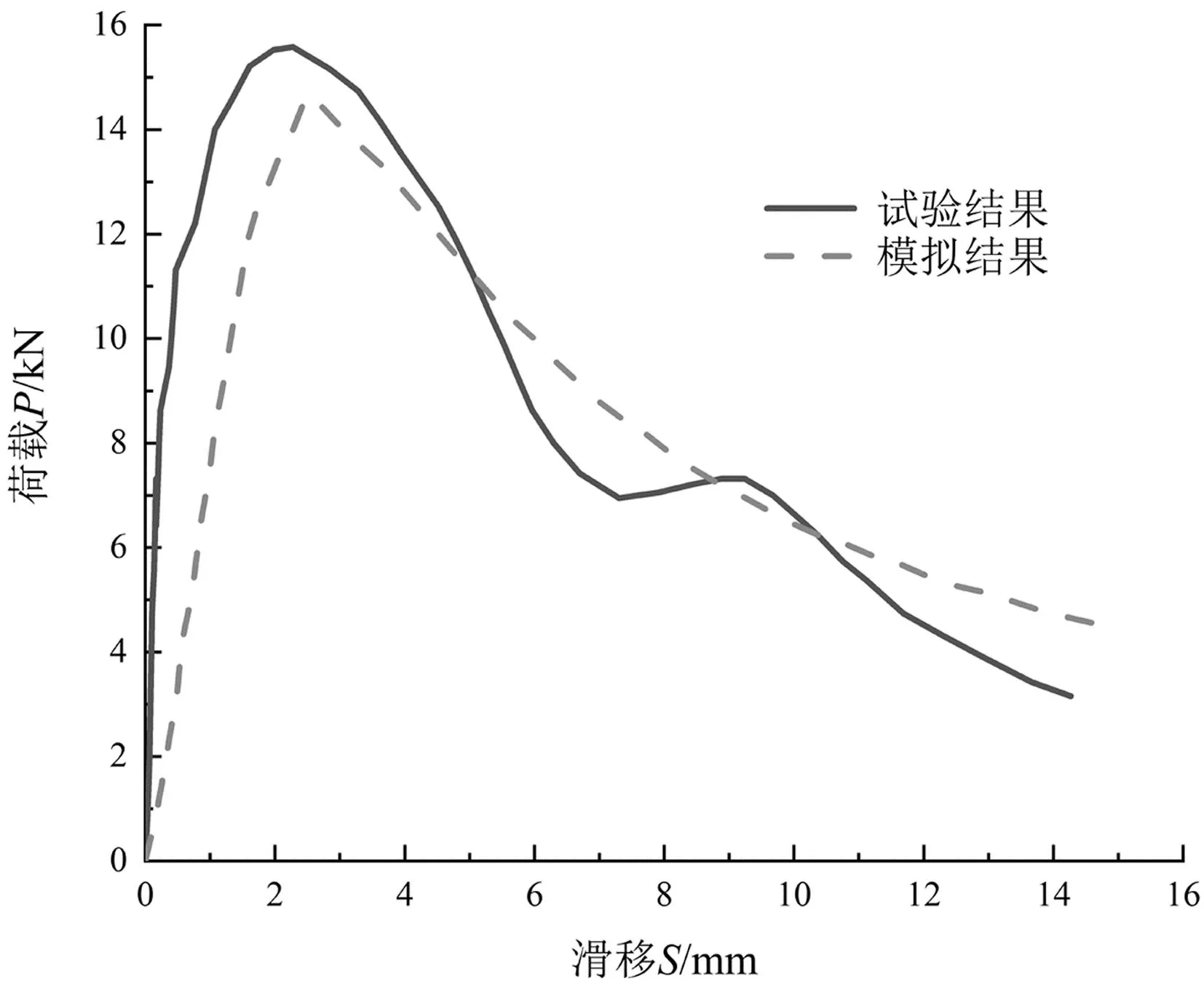
(a)T=60 ℃
不同温度下试件主要结果的模拟值与试验值比较如表2所示。

表2 不同温度下试件主要结果的模拟值与试验值比较
3 植筋套筒拉拔性能的模拟分析
以温度T(20、60、80、100、120、160、200 ℃)、植筋深度与直径比la/d(2.5、3、4、5)等为模拟参数进行28个试件分析。套筒材料为45号碳素钢,套筒外径为40 mm,植筋端内径为20 mm,用以植入直径d=16 mm的HRB400级钢筋,植筋深度la分别为2.5d、3d、4d和5d。另一端内径为24 mm,用以拧入螺杆。钢套筒植筋试件见图4。
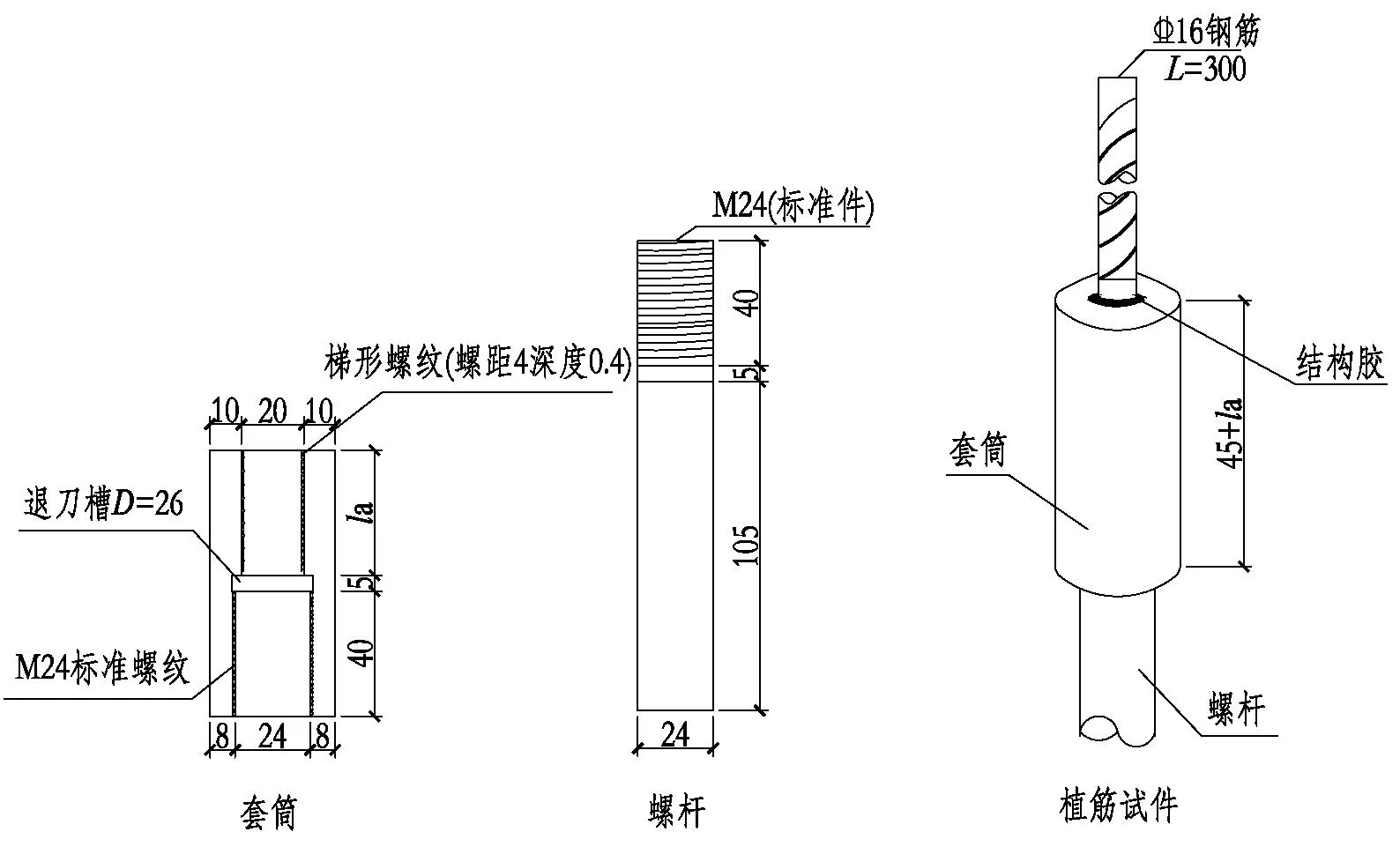
图4 钢套筒植筋试件(单位:mm)
3.1 温度的影响
图5为la/d=3,d=16 mm时,试件在不同温度下的荷载-滑移(P-S)曲线;图6为la/d=3,d=16 mm时,植筋试件拉拔承载力降低系数(Pu,i/Pu)与温度(T)的关系;表3给出了la/d=3,d=16 mm时,试件在不同温度下的主要分析结果。

表3 不同温度下各试件主要分析结果

图5 不同温度下试件荷载-滑移曲线
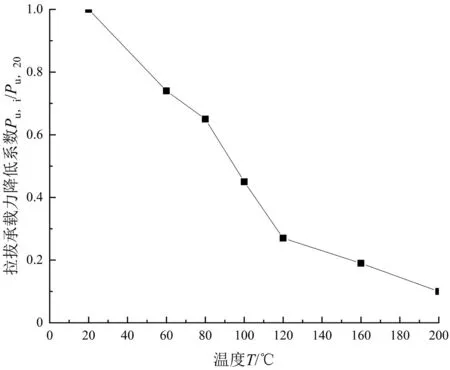
图6 拉拔承载力降低系数与温度关系图
由图5、图6、表3可知,随着温度的升高,植筋套筒试件的拉拔承载力与拉拔承载力对应的滑移量逐渐降低。温度为60、80、100、120、160、200 ℃时,试件的拉拔承载力分别为常温(20 ℃)试件拉拔承载力的74%、65%、46%、27%、20%、10%。当当温度达到100 ℃时,植筋套筒试件的拉拔承载力约为常温时的50%。温度达到200 ℃时,植筋套筒拉拔承载力仅为常温时的10%,基本丧失承载力。
图7为不同温度下,拉拔极限承载力时,植筋应力沿锚固长度的分布规律。由图7可见,植筋的应力随着其埋深的增加而逐渐减小,越是靠近套筒顶部应力就越大,植筋钢筋在整个拉拔过程中没有屈服。
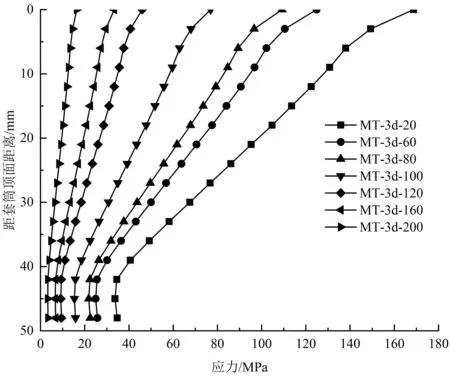
图7 极限荷载下植筋应力沿锚固长度的分布规律
3.2 植筋深度与直径比(la/d)的影响
图8分别给出了la/d为2.5、4、5,d=16 mm时,试件在不同温度下的荷载-滑移(P-S)曲线;图9分别给出各个温度下,la/d为2.5、3、4、5,d=16 mm时,试件的荷载-滑移(P-S)曲线;图10给出了la/d为2.5、4、5,d=16 mm时,试件拉拔承载力与温度的关系(P-T)。
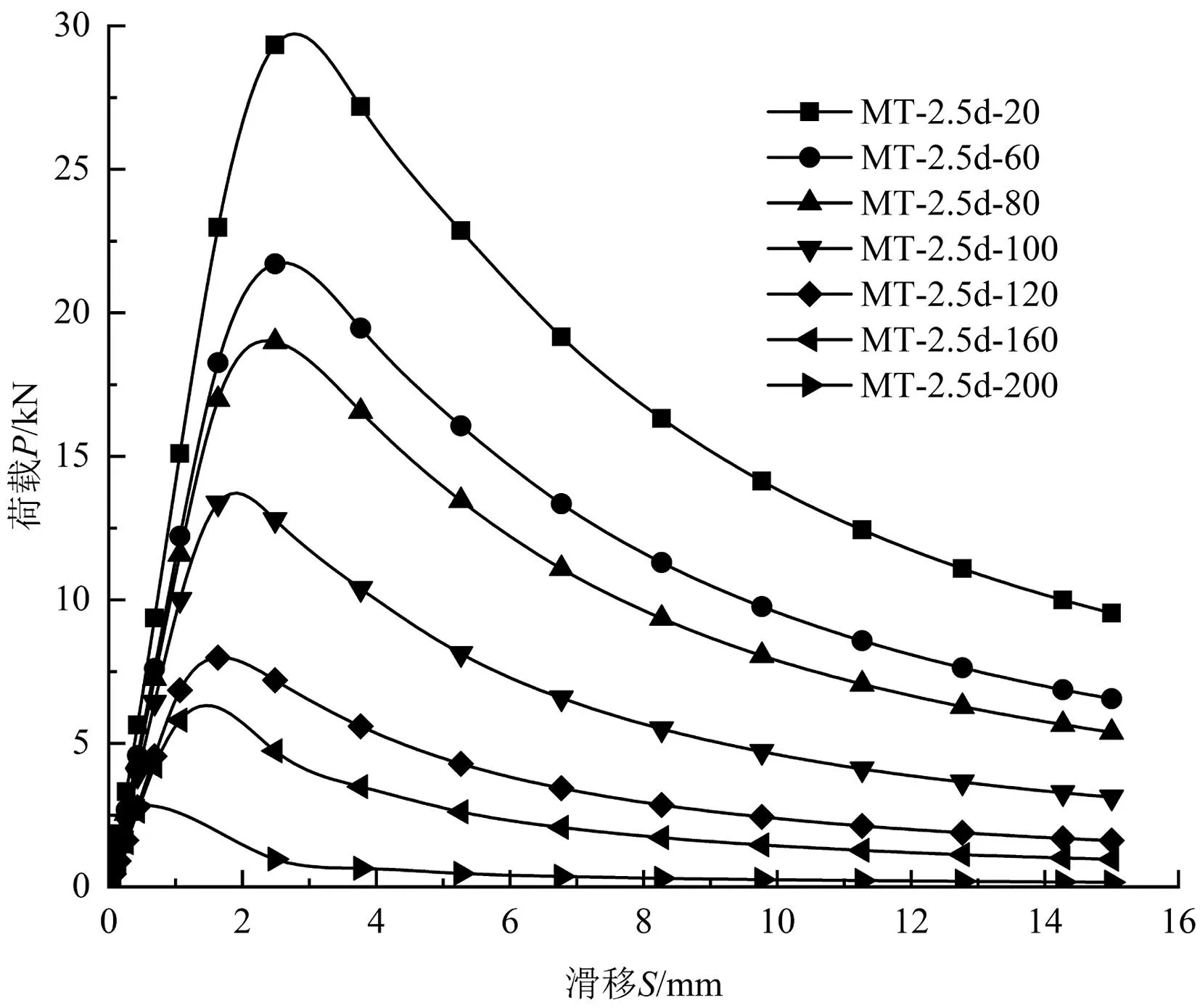
(a)la/d=2.5

(a)T=20 ℃

图10 不同la/d下拉拔承载力与温度关系图
由图8、图10可见,在植筋深度与直径比la/d相同的情况下,随着植筋受热温度的升高,植筋试件的拉拔承载力降低,拉拔承载力对应的滑移也逐渐减小。随着试件受热温度的升高,植筋试件P-S曲线的斜率逐渐减小,这表明植筋黏结刚度随温度升高而降低;在温度低于120 ℃时,黏结刚度降低不明显,温度高于120 ℃时,黏结刚度随试件温度升高而降低显著。
由图9可见,在受热温度相同的情况下,植筋深度与直径比la/d的增大,可使植筋拉拔承载力增大;由图10也可看出,植筋深度与直径比la/d越大,温度对于拉拔承载力的影响越小,la/d为3、4、5的试件在各个温度下的拉拔承载力分别为相同温度下la/d为2.5试件拉拔承载力的1.20倍、1.33倍、1.67倍左右。
4 黏结应力位置函数
黏结-滑移本构关系是根据平均黏结强度理论得到的,主要反映界面之间的黏结力的水平变化,而计算得到的是植筋界面之间的平均黏结力大小。但是实际情况下,在滑移界面之间黏结应力沿钢筋埋深的方向并非均匀分布。在受力过程中,需要考虑界面间的变形协调,黏结应力并非线性分布,通过位置函数可以清楚描述出黏结应力沿着钢筋埋深方向的分布规律。
在有限元模拟过程中,在场输出中勾选“NFORC,单元应力导致的节点力”并沿着一纵列弹簧方向建立节点集(set-point),在有限元分析结束之后,在运行结果中选择ODB场变量输出,输出变量位置选择唯一单元节点NFORC3,单元/节点选择节点集set-point,得到沿着钢筋埋深方向分布的一列非线性弹簧,以及植筋试件在拉拔过程中黏结应力在埋深方向的分布。
为了将不同温度下黏结应力分布曲线统一到同一坐标轴,将有限元模拟得到的黏结应力的分布曲线根据埋深的方向进行归一化处理,这样可以使不同温度模拟出的结果放在同一坐标轴上进行分析,x坐标轴是相对埋深比,y坐标轴是相对黏结应力,如图11所示。
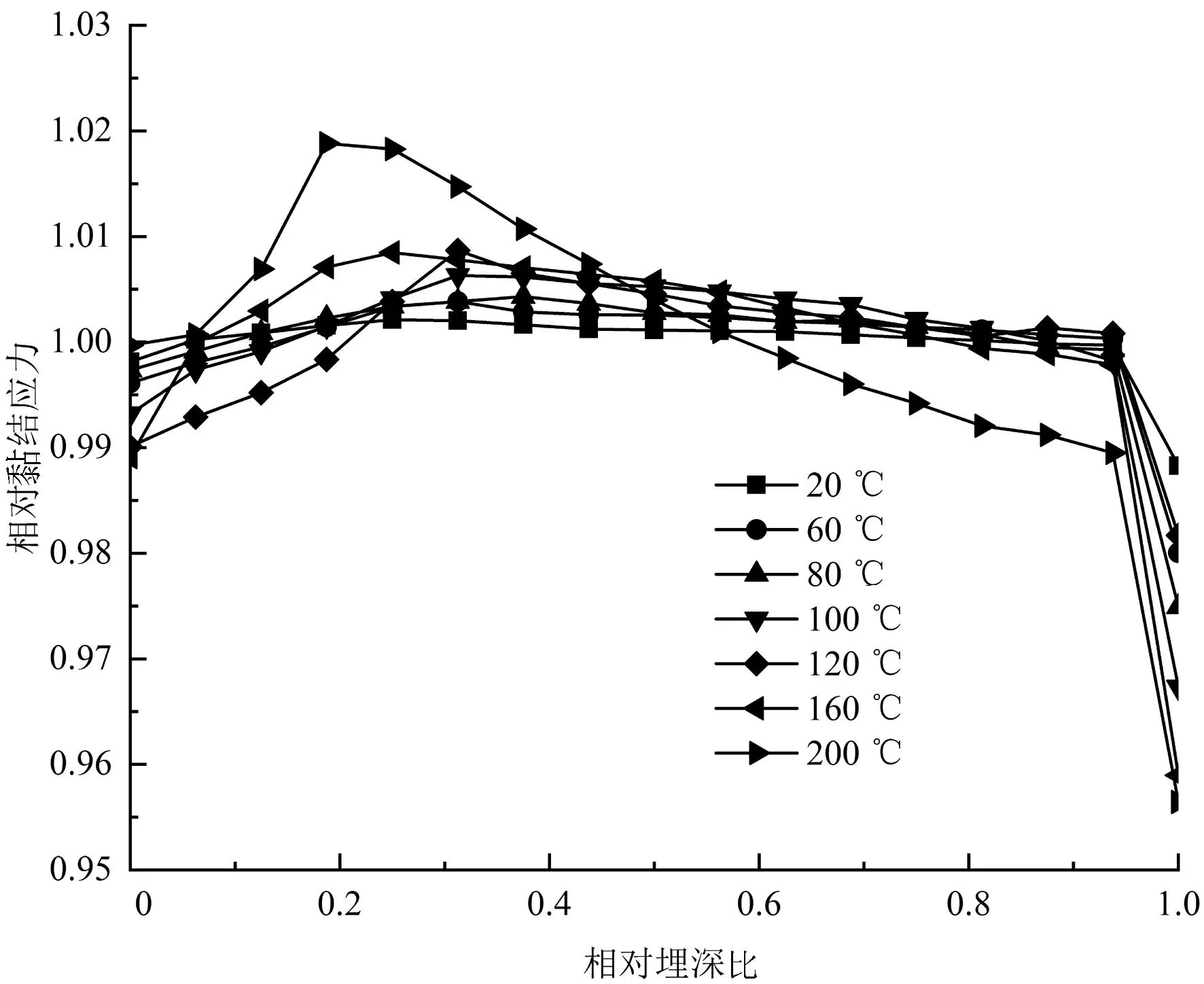
图11 峰值荷载阶段黏结应力位置函数曲线
模拟得到的黏结应力位置函数与文献[5]中得到的黏结应力位置函数的分布趋势一致,利用文献[5]中给出的位置函数折线模型进行简化处理,简化模型如图12所示,模型由3条折线组成,4个控制点为A(0,y0)、B(x1,y1)、C(x2,y2)及D(1.0,y3),位置函数折线模型中各特征点坐标值见表4。

表4 各特征点坐标值
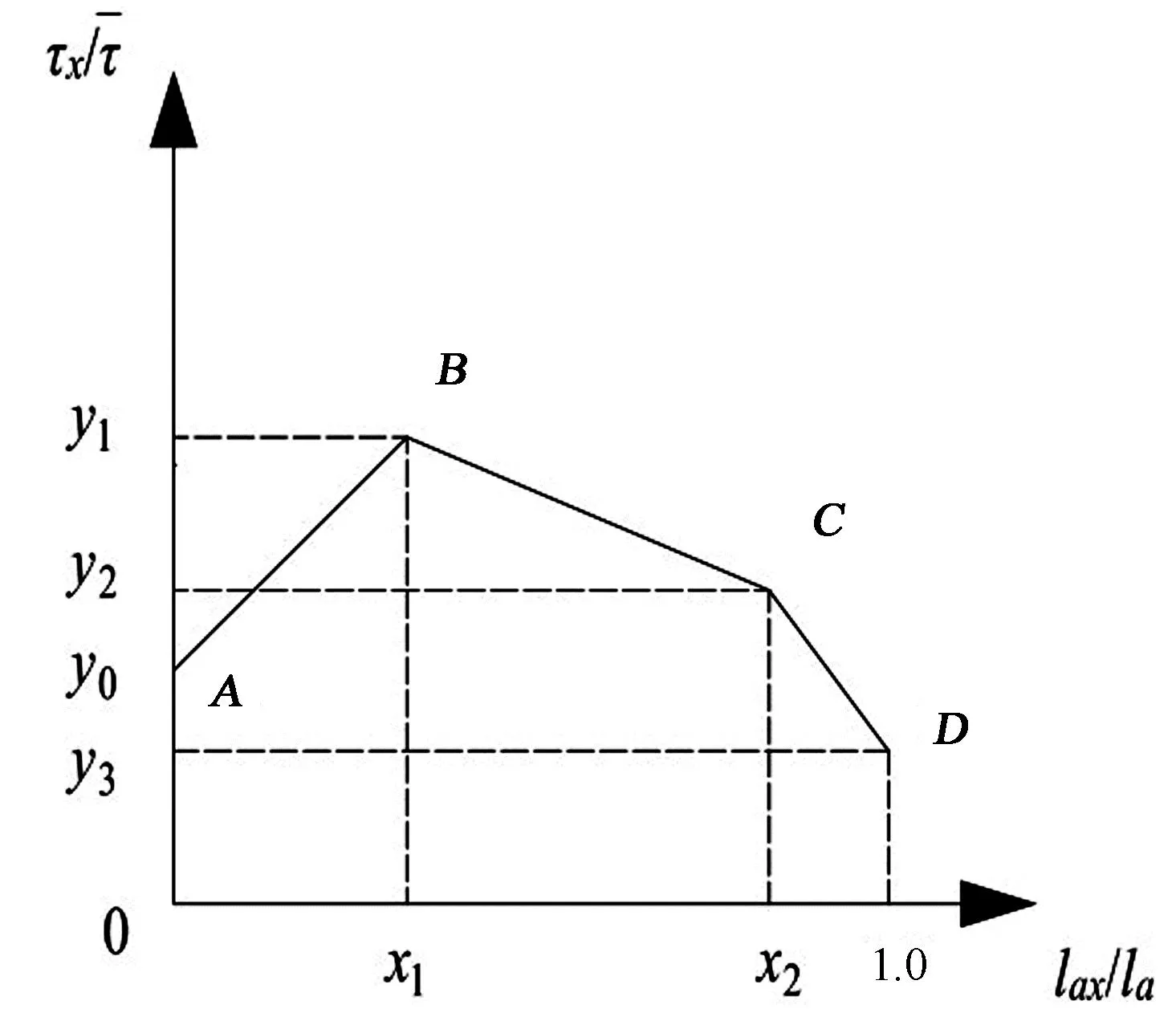
图12 位置函数折线模型
由表4可以看出,各个温度下黏结应力位置函数特征点坐标值相差很小,并且当温度低于200 ℃时,钢材的力学性能也没有明显改变,只有植筋胶的力学性能发生变化,而这种变化在基本本构关系中已经表达,因此黏结应力位置函数不考虑温度影响。取各特征点值A(0,0.994 8),B(0.30,1.007 0),C(0.90,0.993 8)和D(1.0,0.972 5),则黏结应力位置函数表达式如下:
(11)
5 结论
1)随着温度的增加,植筋试件的拉拔承载力降低,模拟温度为60、80、100、120、160、200 ℃时拉拔承载力为常温(20 ℃)的74%、65%、46%、27%、20%、10%。当温度达到100 ℃时,植筋试件的承载力约为常温时的50%。
2)植筋深度与直径比la/d相同时,随着温度升高,植筋试件拉拔承载力和拉拔承载力对应滑移逐渐减小。
3)试件受热温度相同时,随着植筋深度与直径比la/d的增加,试件的极限承载力增大,温度相同时,la/d为3、4、5的试件拉拔承载力分别为la/d为2.5试件拉拔承载力的1.20倍、1.33倍、1.67倍左右。在温度低于200 ℃时,la/d的增大可以提高高温下植筋的拉拔承载力。
4)根据模拟结果,得到胶-筋界面黏结应力沿钢筋埋深方向的位置函数模型和表达式。

