饱和欠固结土竖井地基固结分析——以坝前淤积土为例*

张志龙 王红雨

(宁夏大学土木与水利工程学院,银川 750021,中国)

0 引 言

筑坝拦泥淤地,对于防治黄河流域内的水土流失、减少入黄泥沙、巩固退耕还林成果、改善生态环境,促进农村经济发展等方面具有十分重要的意义,是小流域综合治理的一项重要措施。然而,位于黄河上游段的宁夏回族自治区内多数淤地坝建成时间较早,随着逐年淤积,拦蓄库容日趋减小,以致不能拦蓄设计洪水,成为险库险坝。宁夏回族自治区南部黄土丘陵山区淤地坝除险加固工程中,普遍采用在坝前淤积层上直接加高坝体的施工方法。与土坝除险加固工程中加高培厚坝体的其他方法相比,这种工法具有节省填筑土方、缩短工期、减少投资等优势。淤地坝坝前淤积层多为坝址上游小流域内洪水携带的以粉质黏土为主的黄土(王亚峰等,2009),由于坝前沉积环境基本处于静水状态,此类淤积物属于欠固结土,固结过程中往往发生大变形且土体骨架为非线性变形材料(张海丘等,2015; 夏长青等,2018)。因此,针对坝前淤积土基本物理性状和水力特征,选择合适的排水固结计算方法,是保证淤地坝除险加固工程安全的前提条件。

在地基排水固结方法中,竖井固结法因减少了排水路径,缩短固结时间,效果好且投资低,在工程中得到了广泛应用。早期对竖井地基排水固结方法的研究,大多建立在小变形固结理论的基础上,考虑井阻效应、涂抹效应、渗透系数的各向异性、非线性应力-应变关系、可变荷载等因素(Barron,1948; Hansbo,1981; 谢康和等,1989; Tang et al.,2000; Deng et al.,2013; Lu et al.,2015; 秦爱芳等,2021),而对于淤积土这类本构关系为非线性的大变形固结问题已不再适用(张继发等,2003)。国内外有关竖井排水固结的大变形研究还相对较少,江辉煌等(2011)基于大变形理论,考虑土体本构关系为非线性条件并采用差分方法求解固结过程,建立了竖井地基大变形固结方程。Townsend et al.(1990)认为分段线性模型更适用于土体的大变形、非线性的本构关系,在模型的初始条件、边界条件和土壤非均质性方面具有更大的通用性。Fox et al.(2003)基于分段线性差分方法,提出了竖井地基大应变径向固结模型(RCS1),该模型能够考虑土的竖向应变、渗透系数之间的差异性,能够较好地应用于饱和软土大变形竖井地基固结。然而,RCS1模型主要是针对正常固结土进行竖井地基堆载的固结计算,坝前淤积土为欠固结土,许多学者研究表明,确定欠固结土的排水固结性状需要考虑自重固结因素(McVay et al.,1986; 谢新宇等,2005; 史玉金等,2007; 张明等,2012),采用正常固结竖井地基模型计算欠固结土的固结问题,是否会影响计算的准确性,有待进一步研究。

坝前淤积面加坝工法包括放空库容、晾晒淤积面、铺设垫层、加高坝体等工序。因此,采用该工法施工,需要考虑坝前淤积土体在晾晒期间的自重固结和增设塑料排水板后施加外荷载所引起的固结,这使得计算比较复杂,对此问题的研究还相对较少。

本文考虑天然淤积土在自重应力作用下产生超静孔压进而发生固结的因素,在RCS1模型基础上,基于分段线性方法嵌入了一维自重固结计算程序,建立欠固结竖井地基固结模型(RSUC)来探究欠固结与正常固结竖井地基固结过程的差异。利用相关工程案例分析计算淤积土晾晒期间自重固结下竖井地基固结规律,并与无排水板工况进行对比分析,以期为淤地坝除险加固工程的理论计算与施工方案提供参考。

1 RSUC模型的建立

RSUC模型由两部分组成,第1部分为欠固结土自重固结,计算淤积土晾晒期间仅在自重作用下的固结,该部分用来确定淤积土前期的“欠固结”状态,为后期计算提供相应参数; 第2部分为竖井地基堆载固结,确定淤积土在堆载作用下埋设塑料排水板后的固结过程。模型计算流程如图1所示。

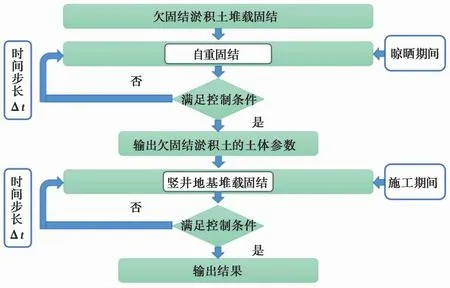
图1 RSUC模型计算流程图

1.1 自重固结计算方法

自重固结计算方法采用大变形固结理论计算饱和淤积土的固结问题,使用分段线性有限差分方法求解偏微分方程。计算过程中基于有效应力、渗透系数与孔隙比之间的基本关系,在一个时间增量Δt下,以一个土体单元为研究对象,通过有效应力原理利用自重和静水压力之和作为总应力来计算单元孔隙水的净流出,并以单元压缩量等于孔隙水的净流出作为基本条件进行迭代计算。

考虑自重固结与后期竖井地基固结衔接的准确性,故将自重固结模块的几何条件设立如图2,模型的建立仍为圆形土柱为例。指定土层相应截面为网格对称中心,土层的底部作为坐标轴的基准面,模型的上边界和下边界可以根据淤积层的实际情况设置为透水层和不透水层。当t=0时刻,淤积土层的初始厚度为H0,上下边界总水头值为hwt、hwb,土层竖向划分为Rj个单元,径向Rs个环形单元(环形单元的设立,为后期竖井地基固结的几何模型提供相对应的数据)。定义径向和垂直坐标为r和z,中心线向外为正,单元节点坐标i和j的定义类似。每个环形单元具有相同宽度Δri、高度L0=H0/Rj、体积V0=2πriΔriL0,以及位于径向坐标ri和标高zij=(j-0.5)L0处的中心节点ij。

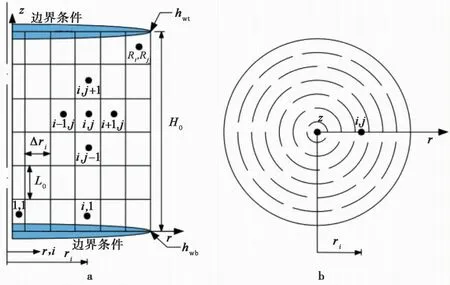
图2 自重固结计算网格划分示意图

RSUC模型做出如下假设:(1)土体是均质材料; (2)土粒和孔隙水不可压缩; (3)用坐标点定义土体的本构关系是非线性的; (4)模型只考虑竖向应变; (5)模型的几何形状、材料特性、单元流量和其他相应变量都在每个时间步长相对于固定坐标系进行更新。

1.1.1 本构关系

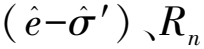
图3 本构关系

1.1.2 单元节点总应力

自重固结计算方法中单元节点ij总应力仅为土体自重和静水压力之和:

(1)

(2)

1.1.3 渗流流量及沉降

相邻单元节点ij和i,j+1之间的相对渗流量计算如下:

(3)

(4)

(5)

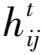
t+Δt时刻,土体单元ij新的体积可以根据相邻单元孔隙水流入和流出的差值得出:

(6)

自重固结计算方法在单元参数进行更新过程中,保持每个单元固体质量即固体颗粒在固结过程中不跨越单元边界。故在t+Δt时刻,单元ij新的孔隙比、环形单元i的沉降量为:

(7)

(8)

1.1.4 边界条件

土层边界条件的设立可根据淤积土层的实际情况设置为透水或者不透水边界,模型涉及到的边界条件如表1所示。

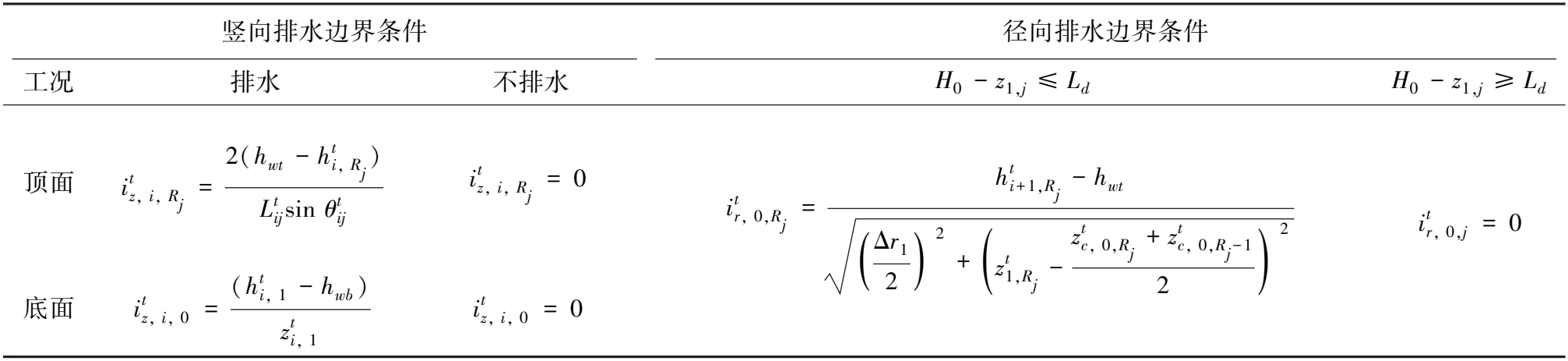
表1 模型边界条件

1.1.5 孔隙压力、有效应力及固结度

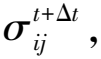
(9)

土层平均固结度为:

(10)

式中:S*为土层的最终沉降量,自重固结相应计算流程见图4。

图4 自重固结计算流程图

1.1.6 时间增量

自重固结计算方法在每个时间步长内采用两个标准来控制时间增量Δt的值,第一个标准为使用显式有限差分法对抛物线型太沙基固结方程进行求解:

(11)

式中:Cv为固结系数。运用显式差分格式,则:

(12)

(13)

将式(12)、式(13)代入式(11)中,整理得:

(14)

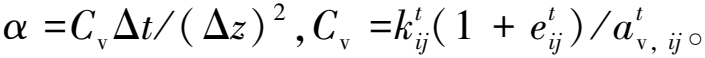
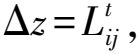
(15)

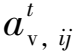
考虑到排水边界处较高的初始渗流速度可能导致式(15)计算的时间增量值较大,因此定义了第2个时间标准增量,以提高早期固结阶段的计算精度:

(16)

式(16)确保在时间增量Δt下,每个单元的垂直应变不会超过该单元最终应变的0.1%。因此,自重固结计算程序在每个时间步长下计算时间增量时,取两个标准的最小值(式(15)、式(16)的最小值),此后运用该值对单元的参数进行更新。

1.2 竖井地基堆载固结计算方法

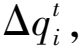
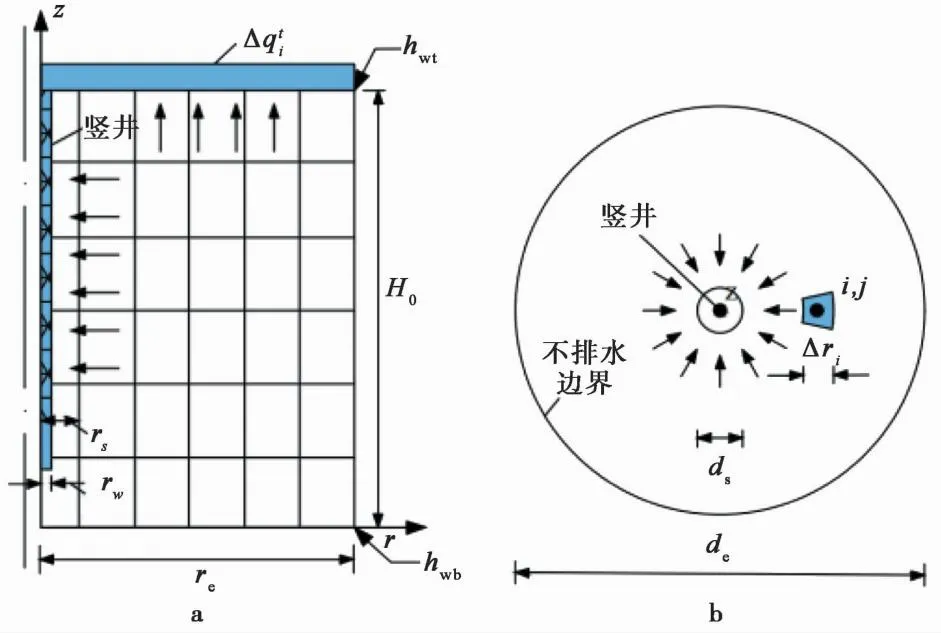
图5 竖井地基固结示意图

竖井堆载预压固结计算用于施工期加高坝体,利用坝体的重量加速淤积土的固结,其本质为竖井地基条件下增加上覆荷载加速土层自身固结过程,此时,计算应用场景与RCS1模型一致。加载前,需将自重固结计算完成时土体内Ri×Rj个单元的数据一一对应直接赋值给竖井堆载预压固结计算的Ri×Rj个单元即可。

1.2.1 竖井地基堆载固结过程

单元节点ij在t时刻的总应力为该节点上方土体自重、静水压力、上覆荷载之和,由于土体用于竖井地基固结的初始参数由自重固结计算结果赋予,故无初始荷载q0。其计算式如下:

(17)

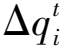
对于模型的孔隙水压力、等效渗透系数、单元流量、体积更新、平均沉降、平均固结度等计算公式参考RCS1模型,详见文献(Fox et al.,2003)。

作者采用Fortran语言自行编写了RSUC模型计算程序,完成了本文数值模拟计算。

2 模型验证

2.1 自重固结计算方法验证

McVay et al.(1986)为了预测土堤的淤积能力和进行填筑所需要的时间,使用磷酸盐淤积土开展了大型的自重固结现场试验。在该试验中,土体的初始厚度H0为6.33m,土粒的相对密度Gs为2.71,根据现场测量土层初始孔隙比沿深度变化,已发生一定程度自重固结(图6),但影响较小,在模型计算中取其平均值18.8。边界条件仅设置为上边界排水,模型单元数量设置为Ri=Rj=100,计算过程中土体的有效应力和渗透系数取值为(压缩特性和渗透特性):

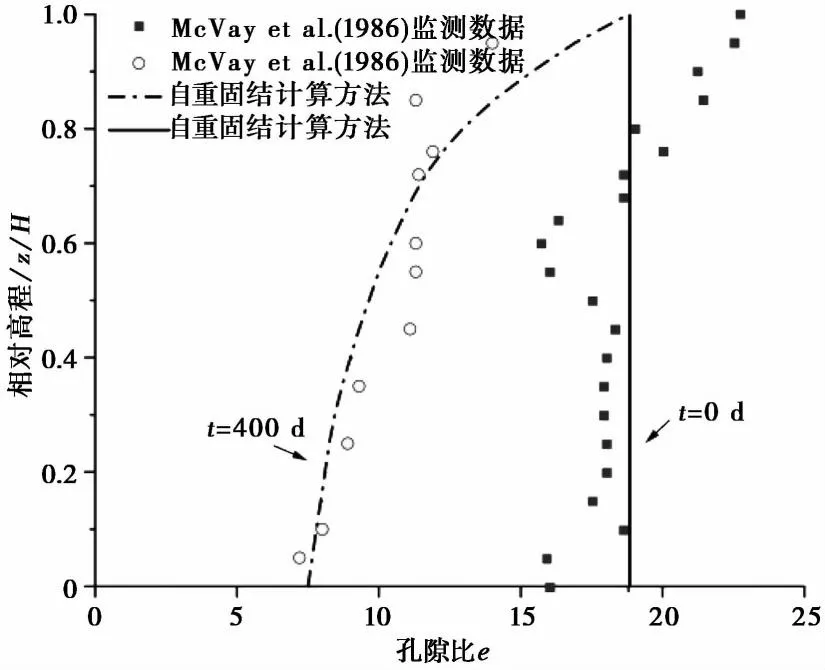
图6 孔隙比监测与模拟结果对比图

e=12.19σ′-0.29

(18)

k=1.41×10-11e4.11

(19)

式中:σ′为有效应力(kPa);k为渗透系数(m·s-1)。

自重固结计算结果与现场测得的孔隙比分布情况见图6。结合淤积土实际分布情况,在模型计算中假设土层初始孔隙比是均匀分布的。在自重固结400d时,自重固结方法计算的孔隙比分布与现场试验监测值吻合较好。

图7为土体沉降过程曲线,计算结果能够较好地吻合现场实测数据,表明自重固结计算方法对土体自重固结沉降的模拟准确性较高。在整个过程中,土体总沉降量为2.7m,占初始高度的42.7%,属于大变形固结问题; 另外,土体的平均孔隙比由初始的18.8减小到最终的9.75,减小了51.9%,土层的渗透系数由初始2.43×10-6m·s-1减小到最终的1.64×10-7m·s-1,减小了93.26%,对应的平均压缩系数和固结系数在土体的固结过程中均发生了变化,也属于土体本构关系的非线性问题。该实例表明,自重固结计算方法能够较为准确地计算淤积土这类材料非线性且固结过程中发生大变形的自重固结过程。

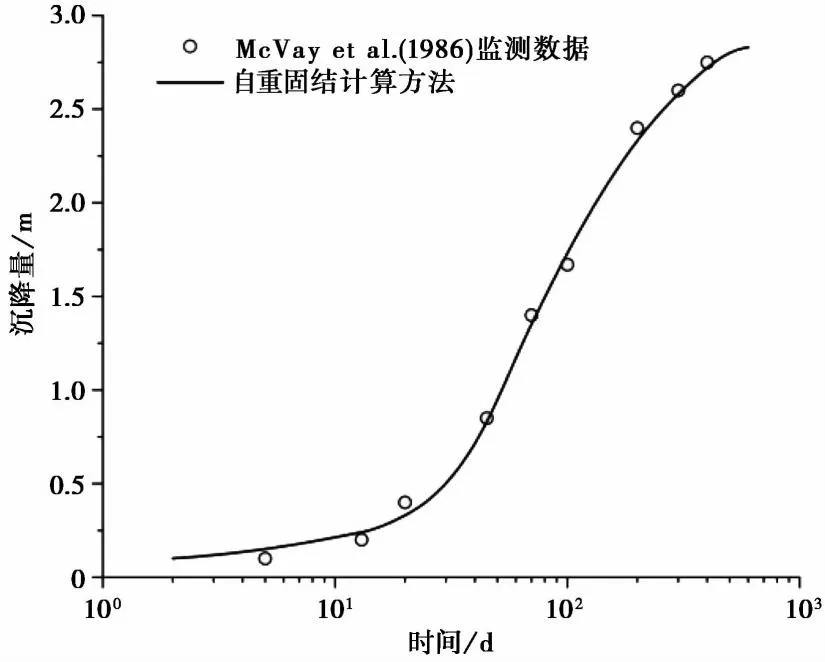
图7 文献沉降量监测与模拟结果对比图

2.2 RSUC计算模型的验证

参考Indraratna et al.(1994)对堤坝工程在堆载条件下增设塑料排水板的沉降监测值,验证本文RSUC模型整体的准确性和适用性。

该工程位于马来西亚Muar海岸,地基主要为淤泥质土,且加固前处于欠固结状态。土层计算参数见表2,其中,Cc为土体压缩指数,Ck为e-logk的斜率,e0为初始孔隙比。塑料排水板打穿淤积层,并以三角形方式布置,间距S=1.3m,排水板直径dw=0.07m,排水板影响直径de=1.365m。

表2 土层参数

通常考虑涂抹效应时,其等效半径rs=2rw,则rs=0.07m,涂抹区渗透系数比η=kr/ksr=1.3。大多数塑料排水板正常工作时其排水能力已超过100～150m3·a-1,可忽略井阻效应的影响(Hansbo,1993;Yeung,1997)。

堆载分两个阶段来施加,如图8所示,第1阶段于初始14d内加高至2.57m,堆载52.68kPa,105d后开始进行第2阶段的加载过程,24d内填方高度至4.74m,堆载97.17kPa,总的现场监测时间为400d(土层重度按20.5kN·m-3计算),忽略填方高度对数值预测的影响,将填方过程视为在两个施工阶段施加于基础表面的等应力荷载。

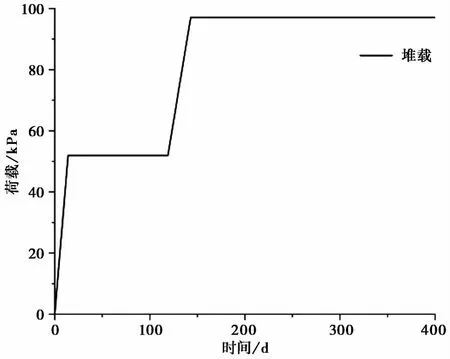
图8 荷载-时间曲线

RSUC模型计算的土层沉降与现场实测结果对比见图9,从图中可以看出RSUC模型较好地预测了堆载条件下增设塑料排水管后淤泥土固结过程中的沉降变化,模型计算的最终沉降量与实际监测值相差0.08m,计算结果与实测值比较接近。

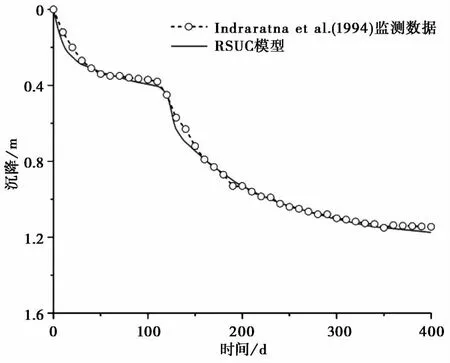
图9 沉降监测与模拟结果对比图

2.3 RSUC模型与RCS1模型计算结果对比分析

基于2.2小节算例,假设淤泥层为正常固结土,将RCS1模型的计算结果与RSUC模型进行对比,探究欠固结竖井地基与正常竖井地基堆载固结的差异。

土层超静孔隙水压力消散程度见图10,图中超静孔隙水压力值为100%表示土体内部消散为0。在第1阶段施工结束时(即119d时填土2.57m),欠固结土体内部未消散的超静孔隙水压力由100%下降到20%,而正常固结土体内部未消散的超静孔隙水压力下降到了16%。在第2阶段施工中,经过281d的堆载,欠固结土体内部未消散的超静孔隙水压力由100%下降到了15%,而正常固结土体内部未消散的超静孔隙水压力下降至14%。分析认为,欠固结土层在加载前存在着尚未完全消散的超静孔隙水压力,故在土层的堆载过程中欠固结土层内平均超静孔隙水压力的积累多于正常固结土。此后在孔压消散过程中,由于消散途径一致(竖向和径向渗流),因此在第1阶段施工结束时欠固结土层内未消散的超静孔隙水压力(20%)要大于正常固结土(16%)。在监测时间结束时,由于总堆载时间较长(第1阶段119d,第2阶段281d),欠固结土层内于加载前已存在的那部分超静孔隙水压力已基本消散,所以在固结时间为400d时,欠固结土层内部的超静孔隙水压力(14%)便与正常固结土(15%)相近。

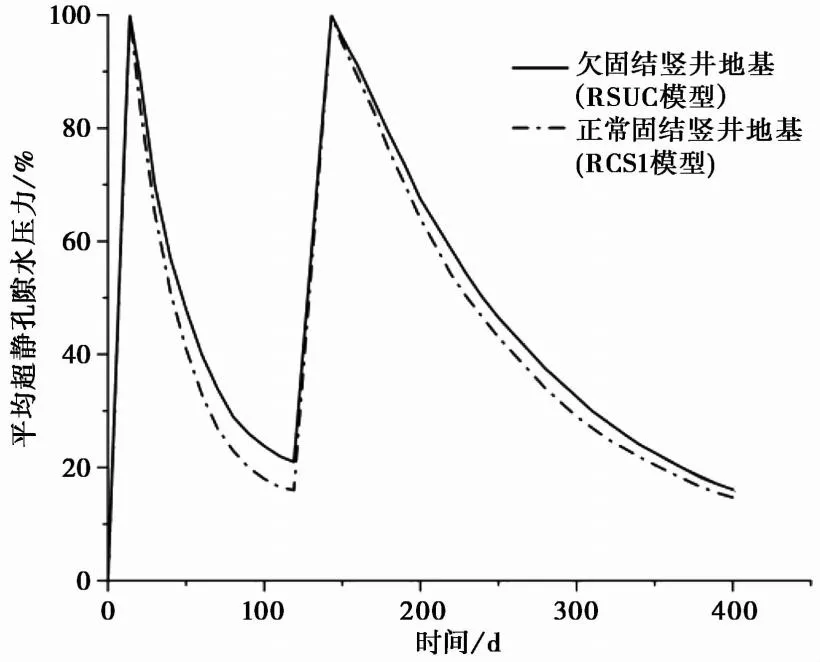
图10 平均超静孔隙水压力百分比

按欠固结土层(RSUC模型)与按正常土层(RSC1模型)计算的竖井地基堆载固结沉降结果对比如图11,由图可知,第1施工阶段结束时,欠固结土与正常固结土沉降结果分别为0.46m、0.49m; 监测结束时,结果分别为1.15m、1.20m。欠固结土与正常固结土虽然沉降结果较为一致,但在两次堆载固结过程中依然存在较大差距。其中:固结时间为50d和210d时,相差结果分别为12.2%(欠固结竖井地基沉降量0.31m,正常固结土沉降量0.39m)和10.1%(欠固结竖井地基沉降量0.89m,正常固结土沉降量1.05m)。分析认为,竖井地基的固结速度规律与一维自重固结不同,一维自重固结土层内超静孔隙水压力越大,固结速度越快; 对于等应力条件下的竖井地基固结则不同,竖井地基排水边界处(塑料排水管周围)土体先行固结,与正常固结土相比,欠固结土层内超静孔压相对较大,排水边界处土体固结速率较快,孔隙比减小也更快,渗透系数和渗流速度随孔隙比的减小而减小,而较低的渗透系数和较小的渗流速度却反过来减缓了排水边界处超孔隙压力的消散速度,因而欠固结竖井地基整体的固结沉降速度比正常固结土慢,固结过程中沉降量较正常固结土小。

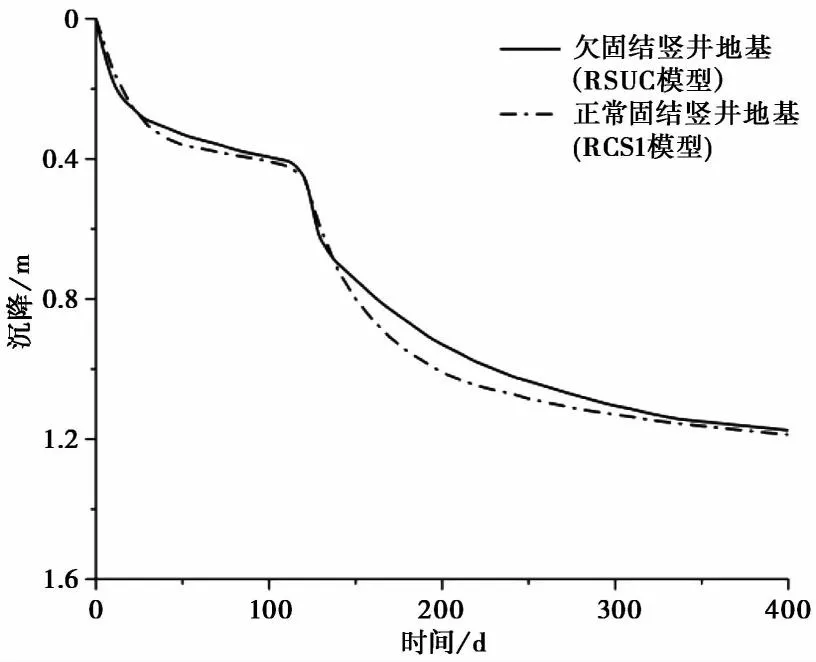
图11 竖井地基沉降结果对比

相同工况下,RSUC模型与RCS1模型计算的沉降值差别较小,但固结过程却有明显差异。本文提出的RSUC模型(欠固结竖井地基模型)的固结速度慢于RCS1模型(正常竖井地基模型),且欠固结土中超静孔隙水压力越大,两个模型计算结果的差异越明显。

3 工程案例

3.1 工程概况

巴家咀水库(殷宗泽等,1979)位于陇东黄土高原沟壑区,1962年建成,坝高58m,总库容2.75亿立方米,土坝为辗压黄土均质坝。由于该地区水土流失问题突出,坝前淤积严重,拦蓄库容日趋减小。于1965年在坝后加高8m,但这种加高坝体方式用土量较大,十分不经济,又于1973年选择在坝体前坡从淤积面起加高土坝,以减少填筑工程量,该坝采用“坝前淤积面加坝”工法加高坝体8m,如图12所示。

图12 巴家咀水库坝前淤积面加坝示意简图

根据坝前淤积面加坝施工工序,进行堆载前需进行放空库容,晾晒淤泥面等工作。期间淤积土仅受自重作用发生固结,由于晾晒期时间较短,坝前淤积土均为欠固结状态。为获得准确的土层参数,运用RSUC模型首先对淤积土在晾晒期间的自重固结进行模拟,设自重固结时间为30d,晾晒期结束后继续进行堆载固结计算。

RSUC模型参数:初始孔隙比设为3.0,土粒比重Gs=2.72,容重为2.01×103kg·m-3,初始渗透系数为4.4×10-8m·s-1。排水板长度Ld为3m,以三角形方式布置,间距S=1.3m,排水板半径rw=0.035m,影响半径re=0.68m。考虑涂抹效应对固结的影响,设其等效半径rs=0.07m,涂抹区渗透系数比η=kr/ksr=1.3为定值。土层竖向网格划分为Rj=100,径向网格划分为Ri=100,上边界条件设为排水状态,其渗透比降iz,i,100随时间不断变化,下边界设为不排水,故iz,i,0=0。计算过程中土体的有效应力和渗透系数取值见式(18)、式(19)。

对文献中原有的A断面结点(编号为119)进行沉降量计算,将119号结点所对应的土层厚度记为H1=3m,上覆荷载70kPa,荷载线性增加(施工260d,停工60d),将H1所对应的单元记为Rm,n,zc,m,n为单元标高,经过时间Δt后,直接由式(20)计算单元Rm,n的沉降量。

(20)

3.2 淤积土自重固结过程

RSUC模型模拟计算淤积土在晾晒期的初始状态为图13。随着时间的增加,淤积土在自重的作用下发生固结,孔隙比与超静孔隙水压力随深度发生变化,晾晒期结束时淤积土的状态如图14。

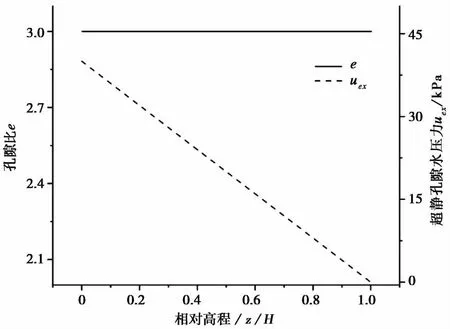
图13 淤积土初始状态

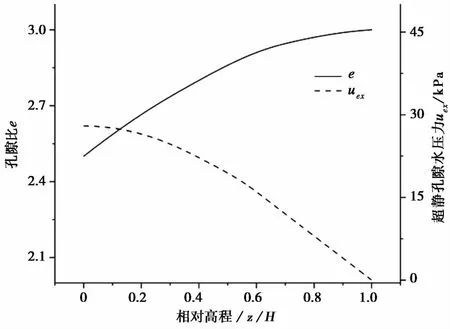
图14 淤积土自重固结30d时的状态

由图14中孔隙比与超静孔压沿土层分布情况可知,孔隙比、超静孔压随相对深度呈非线性变化。淤积土的初始状态为孔隙比沿土层均匀分布(即土层单元初始孔隙比均为e0),土体在自重作用下产生超静孔压进而发生固结,其初始超静孔压沿土层深度线性分布。固结开始后,孔隙水在超静孔隙水压力作用下发生渗流,随着超静孔隙水压力逐渐消散,土层有效应力增加,孔隙比开始减小。由于土层所承受的总应力随深度逐渐增大,土层底部超静孔隙水压力消散速度相对较快,孔隙比变化也就相对较大,进而导致土体底部固结速度相对较快,沉降量较大,而土体表层超静孔隙水压力和孔隙比变化不明显。

3.3 增设塑料排水板对固结沉降的影响

运用RSUC模型、Fox et al.(2003)提出的RCS1模型模拟巴家咀坝前淤积面中增设竖向塑料排水工况,与Fox et al.(1997)(CS2模型)、殷宗泽等(1979)基于比奥固结方程计算的坝前淤积土无排水板条件下固结结果进行对比,探究增设塑料排水板对坝前淤积土固结沉降的影响。

首先计算淤积层超静孔隙水压力随固结时间的消散情况。由计算结果图15可知,加荷70d左右淤积土层内的超静孔压达到最大值,施工时应对这一时段进行重点监测; 由图可知,随着荷载线性增加,超静孔隙水压力的峰值未必出现在施工阶段的末尾(即荷载加荷结束时),而出现在加荷过程中。分析认为,加荷初期土层内部的超静孔隙水压力数值较小,与边界孔压差值小,进而水力梯度小,消散缓慢,继续加荷,使得土层孔压上升占主导地位。当施工加荷70d后,孔压上升达到相当大的数值,此时与边界孔压水头差值较大,水流动快,孔压消散也快,使得加载引起的孔压赶不上边界水头差造成的孔压消散,因此加荷后期孔压下降。

图15 RSUC、RCS1模型与CS2模型模拟结果对比

未布设排水板,CS2模型计算土层内最大平均超静孔隙水压力为46.6kPa。布设排水板后,RSC1模型最大超静孔隙水压力31.9kPa,而RSUC模型中虽累积有自重固结期间尚未完全消散的超静孔压,其最大超静孔隙水压力为34kPa。分析认为,加载过程中土层所受总应力增大,内部表现为超静孔隙水压力的增长,故前期不同工况均出现了孔隙水压力的快速增长并达到最大值; 然而随着外荷载Δq的施加,土层内部也开始了孔隙水压力的消散,消散途径的不同(即增设塑料排水板后,由竖向流增至竖向流、径向流),也导致土层内超静孔隙水压力最终能够达到的峰值不同。可见,增设排水板后,可降低淤积层内的超静孔隙水压力的最大值,增加淤积土坝基的稳定性。此外,增设塑料排水板也提高土体的固结速度,例如时间为130d时,有排水板的土层内超静孔隙水的消散均达到了90%,无排水板的土层则需要320d左右淤积体内超静孔压的消散才能达到90%,因此在相同工况下采用竖井固结法施工可缩短60%左右的工期,这对人工费用较高或者工期较短的工程来说具有重要意义。

增设塑料排水板后土层固结沉降结果如图16,由图可知,由于增设塑料排水板,淤积土层内排水路径增加,土体内水流沿排水板径向和竖向通道溢出,从而缩短了淤积土的固结时间。例如,在施工130d时,CS2模型、殷宗泽等(1979)计算结果分别为15.2cm、15.0cm,则无排水板的土层平均沉降值为15.1cm,RSUC模型、RCS1模型计算结果分别为24.0cm、24.4cm,则有排水板的土层平均沉降值为24.2cm,增设塑料排水板后土层的沉降量是没有排水板土层的1.6倍。此外,现场施工260d后,设置排水板土层的平均工后沉降量为0.6cm,而未设置排水板土层的平均工后沉降量为7.3cm。可见,增设塑料排水板,加大了前期沉降量,减小了工后沉降,有利于坝基稳定。虽然固结后期没有考虑水平位移、应变率、蠕变、次固结沉降等因素,但排水板的安装依然对淤积土的固结有相当大的影响,故在施工设计时,可对加速淤积层的固结效果方案提供参考。

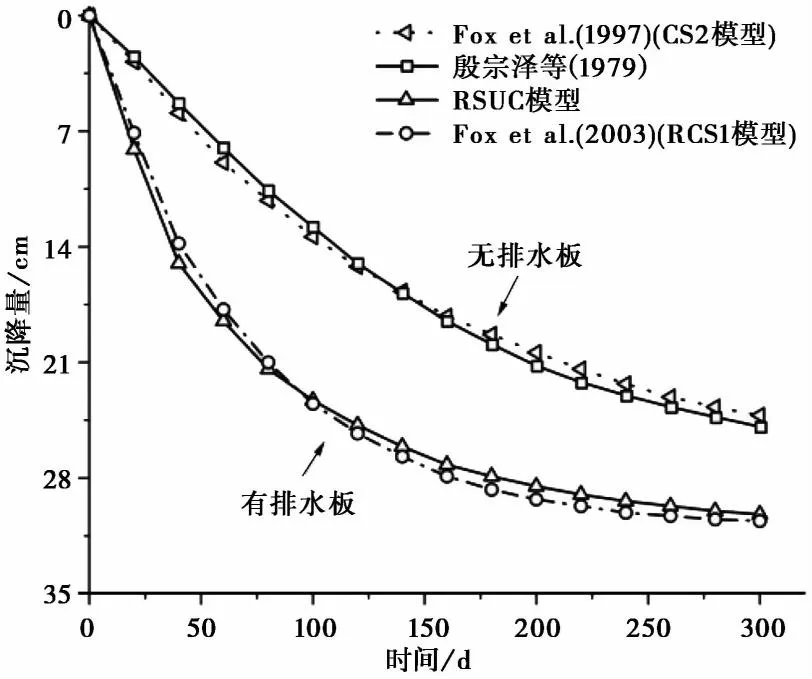
图16 RSUC、RCS1模型与殷宗泽等(1979)模拟结果对比

4 结 论

针对坝前淤积土的特点,本文在RCS1模型的基础上,通过嵌入自重应力固结程序建立了适合计算饱和欠固结土的RSUC模型,拓展了竖井地基固结计算模式,得到如下结论:

(1)嵌入RSUC模型中的采用分段线性方法编制的自重固结计算程序较为准确,模型能够较好地应用于欠固结土竖井地基固结分析。

(2)排水边界处的超静孔隙水压力是造成欠固结与正常固结竖井地基固结差异的主要原因。欠固结竖井地基内较大的超静孔隙水压力使得土体的固结速度慢于正常竖井地基。

(3)坝前淤积土自重固结期间,体内的孔隙比、超静孔压随深度呈非线性变化,土层底部固结速度、超静孔压的消散速度较快,沉降量相对较大。

(4)增设塑料排水板对坝前淤积土的固结效果影响显著,降低了由堆载引起的孔隙水压力峰值,加速淤积层的固结速度,增加前期沉降量,减小工后沉降。