基于服务覆盖的无蜂窝边缘智能网络部署方法

姜静/JIANG Jing，乔东伟/QIAO Dongwei，Worakrin SUTTHIPHAN

（1.西安邮电大学陕西省信息通信网络与安全重点实验室，中国 西安 710121；2.泰国国家电信有限公司，泰国 曼谷 10700）

随着5G网络的规模化部署及新一代信息通信技术的高速发展，信息通信行业面临着日益增长的能耗和碳排放压力。预计到2025年，通信行业将消耗全球20%的电力。为了实施国家的“双碳”战略，工业和信息化部等7个部门联合发布了《信息通信行业绿色低碳发展行动计划（2022-2025年）》，强调未来网络应实现绿色、低碳和高质量发展。运营商希望充分利用各种场景下的业务特征，实现无线服务的按需精准投放，减少网络建设和运营成本，提高资源利用效率和成本效益[1-2]。为了实现该目标，IMT-2030（6G）推进组发布了《6G典型场景和关键能力》白皮书，提出了6G网络应具备按需服务能力。即通过已有业务数据的分析和挖掘，实现个性化和精准的服务供给[3]。因此，绿色低碳发展和按需服务将成为6G网络设计和部署的关键要素，打造更环保、高效和可持续发展的移动通信网络。

无蜂窝大规模多输入多输出（MIMO）于2017年由瑞典林雪平大学的E.G.LARSSON教授和美国纽约大学的T.L.MARZETTA教授在分布式天线系统（DAS）的基础上共同提出，旨在解决5G部署中传统蜂窝通信网络小区间干扰严重、越区切换频繁等问题[4]。无蜂窝大规模MIMO系统在覆盖范围内分布部署大量的无线接入点（AP），通过回程链路与中央处理器（CPU）链接，多个AP形成协作集合为用户提供服务。6G网络在架构层面将通信网络与算力、算法和数据深度融合，构建网络内完整的智能体系。如图1所示，无蜂窝大规模MIMO边缘智能网络在CPU或AP部署移动边缘计算（MEC）服务器，通过MEC的缓存功能显著降低前/后向链路的流量负载和系统能耗，从而解决无蜂窝网络部署时前/后向链路容量受限的瓶颈问题；MEC借助无蜂窝均匀、一致的覆盖性能，提高计算和缓存下载的成功概率[5]。无蜂窝大规模MIMO边缘智能网络结合了MEC和无蜂窝大规模MIMO系统的性能优势，融合通信、计算、存储等功能，具有高效、可靠、低延迟与低成本的优势，成为6G的重要研究方向之一[6-7]。

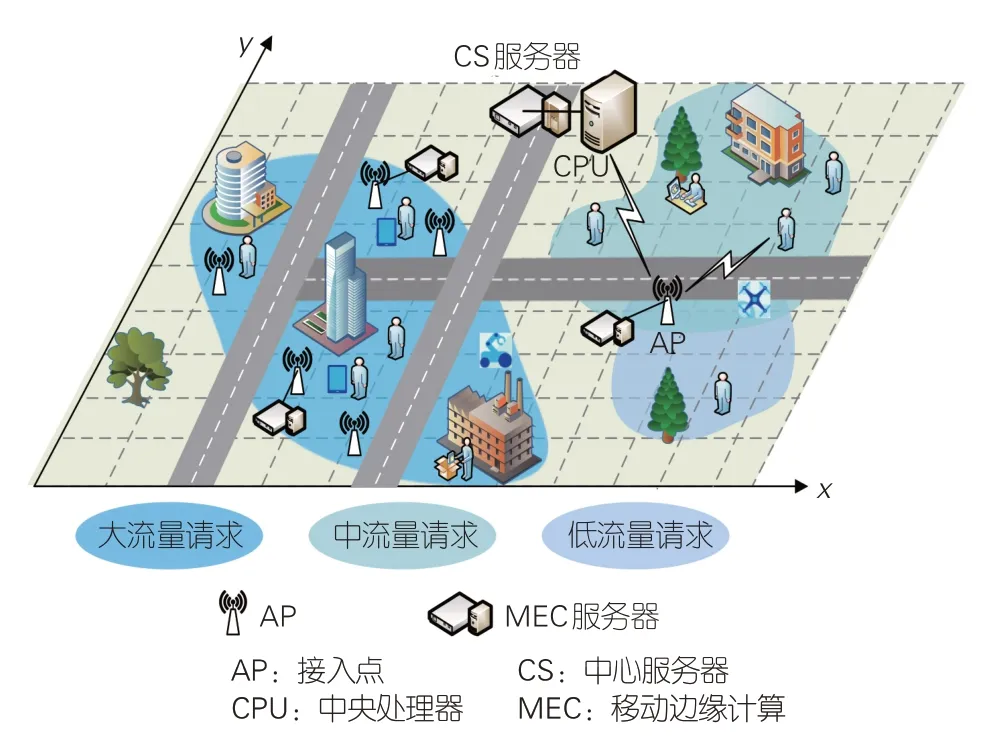
图1 基于服务覆盖的无蜂窝大规模多输入多输出智能网络

传统的无蜂窝大规模MIMO系统假定AP随机、均匀分布在覆盖区域。该假设较为理想化，未充分挖掘无蜂窝网络部署灵活的性能优势。文献[8]首次研究无蜂窝大规模MIMO中的AP位置优化问题，证明了基于最大吞吐量的AP位置优化方法与AP随机部署的传统方案相比，系统总吞吐量提高了3倍；与Lloyd算法（和距离最小）部署方法相比，系统总吞吐量提高了1.25倍。文献[9]将遗传算法（GA）与射线追踪（RT）信道模拟方法相结合，以最大化系统能效为目标生成最佳AP部署方案。上述工作证明了AP部署的优化将显著提高无蜂窝大规模MIMO系统性能。但是，现有研究中无蜂窝大规模MIMO技术的研究通常以系统整体的吞吐量最大、能效最优等作为优化目标[10-12]，未考虑用户和移动业务在不同区域的非均匀分布特性，如何通过无蜂窝网络AP和CPU部署等实现6G精准、个性的服务供给尚未有研究。

为了匹配非均匀的移动业务分布特征，实现按需精准投放，提高资源投入的性价比，服务覆盖作为一种新的网络性能度量被提出[13]。服务覆盖的定义为每覆盖单元的传输容量与业务流量需求的比率，表征了6G网络的服务能力与业务需求之间的匹配程度。文献[14]以最佳服务覆盖为目标，实现覆盖单元的总吞吐量与平均速率需求的比率之和的最大化，以此来优化接入点的部署。构建基于服务覆盖的目标模型可以使无蜂窝大规模MIMO网络达到按需服务的能力。同时，基于多元线性回归模型的梯度下降算法可以求解接入点的位置问题，实现无蜂窝网络业务需求的精准匹配，显著提升系统的能量效率与频谱效率。

针对传统蜂窝网络中MEC服务器的部署问题，文献[15]提出在通信和计算时延受限的条件下，推导MEC系统模型下通信延迟和计算延迟与网络负载和网络资源参数的比例关系，为AP、MEC服务器和中心服务器（CS）的部署提供了理论依据。文献[16]以最大化服务范围内的资源利用率为目标，求解了基于随机部署的MEC服务器最优部署密度。文献[17]利用非均匀泊松点过程模拟MEC服务器的部署过程，求解满足预期业务需求的基站和MEC服务器位置和数量。文献[18]针对由不同传输功率和计算能力的多层异构无线网络，根据MEC服务器的用户类型和AP分层设计求解最优成功边缘计算概率，为MEC的优化配置提供指导。针对无蜂窝大规模MIMO边缘智能网络的MEC服务器部署，文献[6]证明在无蜂窝大规模MIMO边缘智能网络的MEC部署中，CS成功接收到用户的卸载任务的概率随着AP覆盖范围的增大而降低。因此，在给定的成功卸载概率情况下，配置更多的AP将会更节能。但是上述MEC服务器的部署研究尚未解决在考虑通信和计算深度耦合条件下，无蜂窝边缘智能网络如何提供满足多样化业务需求的通信传输能力和算力。

本文将研究基于服务覆盖的无蜂窝网络AP和MEC的联合部署，首先建立多样化业务需求的服务覆盖理论模型，并利用元学习的学习能力，实现多种应用场景和多样化业务需求的服务覆盖建模；然后根据非均匀分布的业务需求，以每个覆盖单元的最佳服务覆盖为目标，研究大规模MIMO无蜂窝网络AP和MEC在多资源约束条件下的联合部署和构型，通过松弛引入辅助变量将非凸离散问题转化为凸连续问题，求解接入点和MEC的联合部署位置，从而实现无蜂窝大规模MIMO网络中与实际业务相匹配的传输能力与协同算力。

1 基于服务覆盖的无蜂窝边缘网络设计

针对多样化的业务需求和应用场景，根据服务覆盖定义结合6G典型应用场景建立多样化的服务覆盖理论模型，进而以最大服务覆盖为目标，设计和优化AP、CPU以及MEC服务器的部署、网络构型、算力资源和频谱资源，实现精准按需服务的无蜂窝大规模MIMO边缘智能网络的传输能力、计算缓存能力和存储能力。

1.1 基于服务覆盖需求统计预测和设计

6G业务丰富多样，每种业务对传输速率、流量密度、空口时延、同步和抖动、移动性、计算时延、计算能力等性能指标的需求有所不同。为精确统计不同业务需求，本文将覆盖区域划分为N个覆盖单元，如图1所示。与文献[13]中服务覆盖定义为传输速率和业务需求速率之比不同，针对多样化的业务需求，本文中我们假设场景的关键服务能力由多个元素组成，例如：传输速率、时延和可靠性要求等，则服务覆盖定义如下：

其中，ant为每种关键能力的加权系数，其取值与该区域的特定业务占比、用户模型等有关，所有关键能力的加权系数之和为1。Ci,i=1,2,3为覆盖单元内可实现的通信和计算能力，Ti,i=1,2,3该区域内不同类型的业务需求。

根据上述定义，我们利用元学习的学习能力不断学习或获取典型场景中的业务特征和关键能力表达，实现多种应用场景和多样化业务需求的服务覆盖建模分析。具体流程如图2所示：首先，定义关键业务需求和服务能力的数据标签和训练样本，嵌入6G典型场景的训练样本；其次，通过实际场景的少量样本，训练和获取不同移动业务的关键技术需求；再次，借助线性分类器产生不同业务的权重系数，平衡多样化业务需求对网络关键服务能力的要求，确定网络的关键服务能力；最后，依据不同覆盖区域的业务需求和关键服务能力，建立服务覆盖模型。利用测试样本完成模型的验证和优化，可以提高服务覆盖的准确性、系统性和科学性。

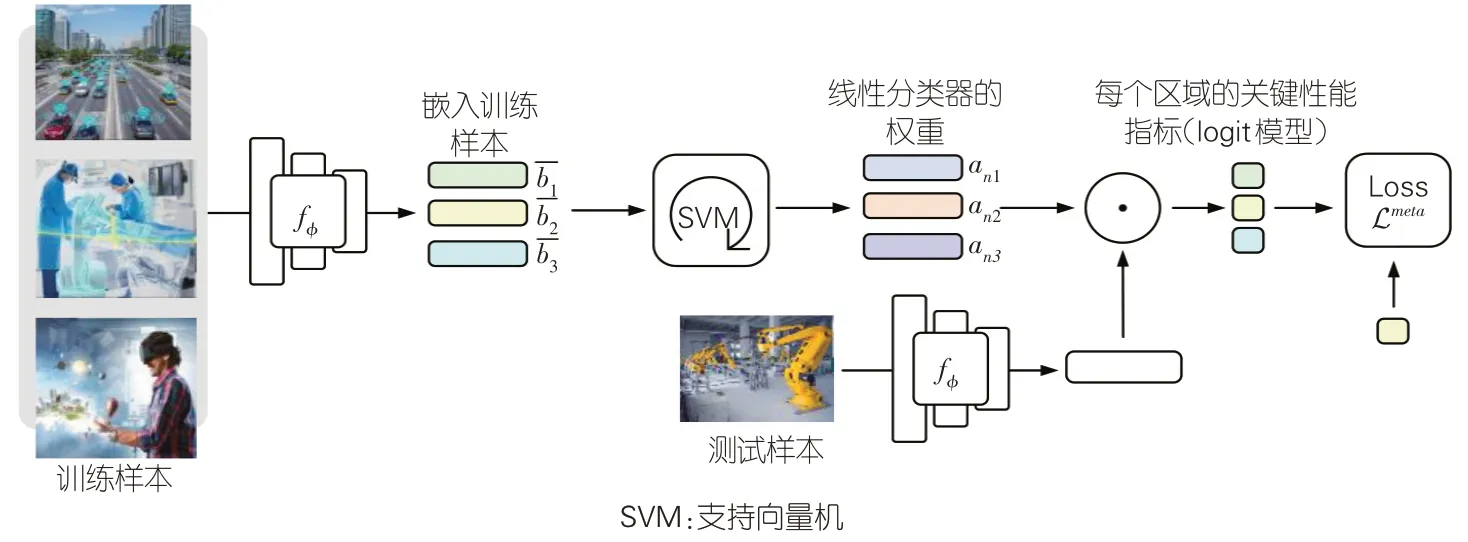
图2 基于元学习的服务覆盖建模分析

1.2 基于服务覆盖的无蜂窝大规模MIMO部署设计

在无蜂窝网络中，AP部署的密度、位置、服务范围决定了AP与用户间的路径损耗，直接影响容量、能耗和通信时延等系统性能。基于服务覆盖的无蜂窝大规模MIMO部署设计将以每个覆盖单元的最佳服务覆盖为目标，通过构建基于AP数量和位置的无蜂窝网络可达速率的闭合表达式，设计大规模MIMO无蜂窝系统的拓扑结构，优化无蜂窝网络的系统性能。在优化的过程中，让每一个覆盖单元的业务需求和传输能力相匹配，可以最小化总覆盖范围内的匹配能力差之和，从而优化每个覆盖单元的精细化服务能力迭代，最终实现无蜂窝网络的按需、精准服务能力。

1.3 基于服务覆盖的无蜂窝边缘智能网络设计

在无蜂窝边缘智能网络中，AP或CPU配置了MEC服务器，网络边缘能够实时存储、下载、处理和分析数据。面对不同应用场景下丰富多样的业务需求，基于服务覆盖的无蜂窝边缘智能网络不仅需要考虑通信需求，还需要考虑算力、计算时延等业务需求的匹配程度。为实现无蜂窝边缘智能网络通信、计算、存储的联合部署，不仅需要优化AP个数和密度、AP部署位置，还需要优化CPU和MEC的算力、MEC部署个数和容量、MEC和AP的连接关系，从而实现与业务需求相匹配的计算、存储和通信能力。进一步地，CPU根据流量负载、缓存和计算需求对通信资源进行动态分配和调度，匹配用户的需求，实现通信和计算能力的协同优化，提升资源利用率和通信计算质量。

2 系统架构与目标函数

针对无蜂窝边缘智能网络中非均匀的通信与计算需求，本文将通过AP和MEC的部署优化，实现与每个覆盖单元业务需求相匹配的计算与通信能力。首先，构建无蜂窝边缘智能网络通信与计算系统模型。其中，通信模型建模了覆盖单元内用户的可达传输速率；计算模型用于表征该覆盖区域内MEC的计算处理能力，用于匹配覆盖单元内用户非均匀的计算任务。其次，分析了无蜂窝边缘智能网络中的通信与计算能力之间的关系。最后，以最大化每个覆盖单元内的服务覆盖为目标，每个覆盖单元获得相匹配的通信计算能力。

2.1 系统模型

在无蜂窝边缘智能网络系统中，我们假设所有AP均配备独立的MEC服务器并通过回程链路连接到CPU，并分布在N个覆盖单元内，如图1所示。假设第m个AP和第k个用户之间的信道表示为：gmk=，其中βmk和hmk分别为大尺度衰落和小尺度衰落，hmk～CN(0,1)。相干周期τc划分为τp个导频传输间隔和τc-τp个上行链路数据传输间隔。第k个用户在相干时间开始同时发送导频序列ψk∈Cτc×1，τp=K。因此，第m个AP处接收到的信号为：

其中，pk=ηk为发射功率，ηk和分别表示第k个用户的功率控制系数和最大上行链路功率。xk表示第k个用户的上行链路数据，ωpm是一个τp维的加性噪声，且满足ωpm～CN(0,1)。

第k个用户的信号通过AP经由CPU被组合成如下解码形式：

其中，z∈RL×1为0和1组成的决策向量，表示为z={z1,z2,…,zL}T,zl=1表示在第l个位置联合部署AP和MEC。γk为第k个用户的信干噪比，k∈Un表示第k个用户位于第n个单元。

假设第k个用户有大小为Tkbits的计算密集型任务，由于移动设备的计算能力和电池容量有限，用户端无法承受高强度的计算任务，因此假设第k个用户将Tkbits任务全部卸载至边缘服务器而不考虑在本地并行计算。当计算任务卸载到边缘服务器时，经历的延迟可以分解为卸载数据的传输延迟和边缘服务器处理的计算延迟。

因此，第n个单元的时延表示为第n个覆盖单元内用户的总时延，具体为：

其中，表示第n个覆盖单元内用户卸载数据到边缘服务器所需的传输延迟；表示第n个单元内边缘服务器处理用户任务的总计算延迟；fmk为连接第m个AP的MEC用于执行第k个用户的处理速度，单位为cycles/s，且fmk≤fmax，fmax为每个边缘服务器处理能力上限；Ncpb为处理1 bit信息所需的周期数，单位为cycles/bit。

2.2 目标函数

本文以实现最大服务覆盖为目标，根据差异化的业务需求设计了无蜂窝边缘智能网络的AP和算力部署，包括MEC的计算能力fmk、MEC服务器个数M、AP和MEC服务器联合部署位置z。假定服务覆盖的关键能力要素包括网络算力、系统时延和通信可达速率，则服务覆盖区域定义如下：

其中，ant∈[0,1]为每种关键能力的加权系数且其取值与该区域的特定业务占比、用户模型等有关。Tn(z)为第n个覆盖区域系统可提供的计算能力，为该区域的算力需求；tn(z)为第n个覆盖区域内用户处理密集型任务可达到的最小时延，为第n个覆盖区域内应满足的最小时延；Cn(z)为第n个覆盖区域系统可提供的传输容量，为第n个位置区域业务传输所需的平均容量。

在无蜂窝边缘智能网络中，针对不同覆盖单元非均匀的通信与计算需求，通过合理的算力资源和AP部署，可以为用户提供低时延、高可靠的通信和计算需求，并满足系统最小计算和通信时延的约束条件。该问题建模为P1：

第1个限制条件中，z表示AP和MEC的部署方案，zl为0或1组成的AP和MEC部署位置元素，通过联合部署实现每个覆盖区域算力和通信需求的精准匹配；第2个限制条件为第n个覆盖单元内，传输和计算时延应小于该单元内移动业务允许的最小时延。σ为冗余因子，为网络业务突发留有合理的传输能力冗余。

3 基于服务覆盖的无蜂窝边缘智能网络部署

P1是一个多目标多约束的混合整数非线性规划问题，首先将覆盖区域内通信和计算能力转化为约束条件，然后利用拉格朗日松弛法和罚函数法对问题中的整数约束进行松弛得到连续非凸问题，最后通过引入辅助变量将非凸目标函数和约束条件进行近似，再利用连续凸逼近算法迭代求解。

首先，问题P1转化为P2：

其中，离散变量zl被松弛为取值范围从0～1的连续变量，然后利用罚函数法使约束条件（16）成为目标函数的一部分，优化问题P2则转换为P3：

其中，μ是惩罚因子，在zl不等于0或1时惩罚目标函数，迫使松弛后的连续变量zl逼近0或1。通过松弛，约束条件（12）-（15）和目标函数中离散变量乘连续变量的结构变成了连续变量乘连续变量的结构，但仍是非凸的，通过引入辅助变量r和新的非凸约束条件，可得：

这时可将P3等价转换为minr。我们设minr可行域为Ω={z,,γk,r}，根据文献[19]先求得（12）-（15）、（17）和（19）这些非负约束条件在可行解Ω(k)处的近似函数，从而得到连续的凸优化问题P4：

s.t.（15），（17），（21），（22），（23），（24）。

其中，（21）-（24）为非凸相乘转化为在可行解Ω(k)处的DC函数近似形式：

凸优化问题P4可以通过内点法或MATLAB的凸优化工具箱（CVX）等方法求解，从而得到最优解对应minr在约束（19）和可行解Ω(k)处近似函数的最小值。根据连续凸逼近，我们令Ω(k+1)=，并将Ω(k+1)作为新的可行解代入问题P4，对新的近似函数进行下一轮凸优化求解，直到结果收敛到局部最优解或不可行解。基于连续凸逼近的迭代算法如算法1。

算法1：基于连续凸逼近的迭代求解算法初始化：定义精度ε，最大迭代次数Imax，迭代序号n=0，惩罚因子η，惩罚因子倍增系数c=2，初始最优值r(0)=inf，设置

4 仿真结果与分析

在仿真过程中，我们首先生成非均匀的用户业务流量场景，并得到该区域的平均流量需求。然后，利用文献[21]中的热点模型生成非均匀分布的用户位置，使用户在热点区域分布得更加密集，在低业务区域分布得更加稀疏，并在该模型下，通过调整热点区域的数量来使用户分布更符合真实场景。我们设置了3个热点区域，利用偏移因子μδ∈[0,1]来表示用户在热点区域中的聚类程度。当μδ=0时，用户均匀分布在覆盖区域内；随着μδ的增加，用户更紧密地分布在热点区域。对于业务流量的产生，假设流量到达遵循泊松过程，那么可以通过设置平均到达率υ来模拟各种不均匀的流量分布。

本文中，我们考虑了一个由M个配备了MEC的AP和K个用户组成的1 km×1 km的无蜂窝大规模MIMO边缘智能网络系统。我们将覆盖区域划分为N个覆盖单元，然后根据服务覆盖对区域内的L个部署点进行M个位置的部署选择。第k个用户和第m个AP之间的小尺度衰落服从hmk～CN(0,1)，大尺度衰落系数建模为：

其中，PLmk表示自由空间路径损耗，表示具有标准差为σsh以及zmk～CN(0,1)的阴影衰落。PLmk采用三斜率模型[20]表示：

其中，

系统的部分仿真参数如表1所示。

▼表1 仿真参数

本文中，我们以不同的方式部署AP，以此来评估和比较基于服务覆盖的AP-MEC部署方法和随机部署方法的系统性能。图3为在非均匀业务需求分布情况下，不同部署AP方法下系统可达容量对比图。图3中的横坐标x、y表示小区覆盖区域的地理位置，纵坐标z表示可实现的吞吐量，用户的业务需求呈非均匀分布，如图3（a）所示。然而，传统的随机部署AP方法实现了均匀一致的覆盖，如图3（b）所示，这造成传输能力在低流量需求区域过剩，高流量需求区域明显不足。图3（c）可以实现与图3（a）流量需求相一致的吞吐量，这证明基于服务覆盖的AP部署方法能够满足热点模型区域所需的业务需求。

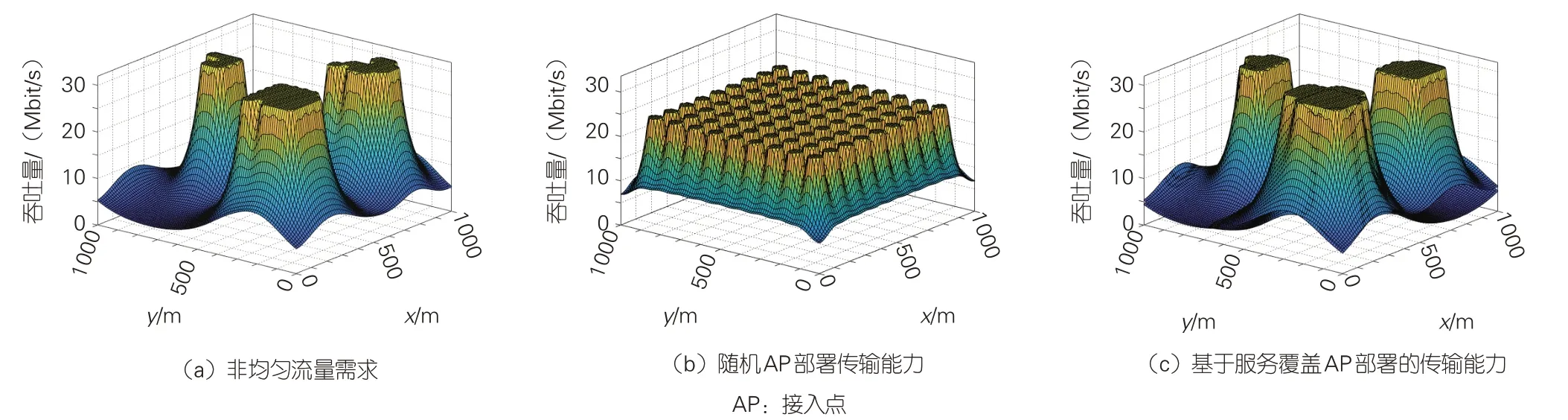
图3 非均匀业务需求和不同部署AP方法下系统的可达容量

图4比较了随机AP部署和基于服务覆盖的AP-MEC部署的平均时延分布图。在随机部署方法下，各覆盖单元可实现的时延均值约为2.5 ms。这是因为随机部署算法由于部署AP位置的随机性，导致某些区域无线网络服务能力不足，产生了业务拥塞，而另一些区域覆盖能力过剩。这种不均衡网络资源分布更容易导致用户的时延超出业务允许的最小时延。而在基于服务覆盖部署AP-MEC方法下，各覆盖单元内可实现的处理时延均值约为0.7 ms，低于各覆盖单元所需的时延均值1.8 ms。这是因为在基于服务覆盖部署方法中，我们在业务需求高的覆盖区域部署了更多的AP，缩短了用户的接入和传输时延，从而提高系统性能和用户体验。

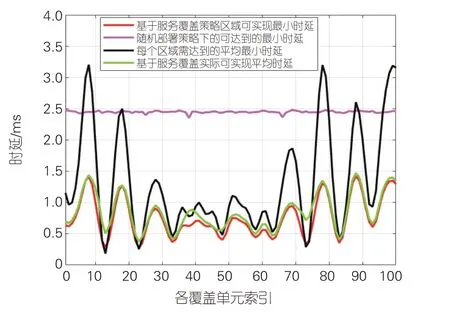
图4 随机部署移动边缘计算和基于服务覆盖部署移动边缘计算的可达最小时延分布

图5为不同AP-MEC部署方法下，每个覆盖单元的通信成功率，即覆盖单元内满足最低通信需求和最低时延的概率。AP-MEC随机部署方法的成功概率均值约为0.754 3，曲线抖动明显，在数据传输过程中会导致数据丢失或重传增加通信的延迟和不稳定性；而基于服务覆盖的通信成功率的均值约为0.945 2，曲线平稳，在高通信成功率区域常伴随着较低的丢包率，有助于提高实时通信应用的质量，证明了基于服务覆盖部署方法能够提供高效稳定的通信。

图5 随机部署和服务覆盖的通信成功率

5 结束语

为解决现有网络以系统整体性能优化为目标，出现的部分服务区域资源浪费和能量损失问题，本文首先引入服务覆盖这一新型网络性能度量，然后针对无蜂窝边缘智能网络提出了一种基于服务覆盖的AP-MEC联合部署方法。通过构建基于元学习的多样化业务需求服务覆盖模型，我们将以每个覆盖单元的最佳服务覆盖为目标来实现系统性能的差异化优化，按需部署网络资源，实现精准的按需服务供给。仿真结果表明，基于服务覆盖的AP-MEC联合部署方法，能够实现系统整体性能的显著提升，同时在不同覆盖单元中实现了精准的按需服务供给，实现高能效、低时延、低能耗的无蜂窝边缘智能网络系统。

在未来的研究过程中，我们将进一步以最佳服务覆盖为目标，提供多场景、多维资源的精准服务，以满足多样化的通信需求，构建高质量、智能化的无蜂窝边缘智能网络系统。