模块化多电平换流器数学建模方法综述

徐梓高,杨桂森,刘瑜超,李彬彬

(1.华北电力大学电气与电子工程学院,北京 100096;2.哈尔滨工程大学智能科学与工程学院,黑龙江 哈尔滨 150001;3.哈尔滨工业大学电气工程及自动化学院,黑龙江 哈尔滨 150001)

0 引 言

我国的大规模新能源外送战略推动远距离、大容量的电力输送技术快速发展。我国的陆上风光能源主要位于西北地区,与东部地区的电力负荷中心呈逆向分布。传统高压交流输电方案在输电距离过长时存在电压降落大、线路成本高等问题,不适用于新能源的远距离外送。面对远距离、大容量的输电需求,高压直流输电技术成为我国陆上西电东送和海上风电西送的首选方案。历经半个多世纪,HVDC系统在新型开关器件与换流器拓扑的推动下不断演化,形成以模块化多电平换流器为核心拓扑的柔性HVDC输电技术,具有电压/功率等级易扩展、潮流控制能力强、输出谐波小、易于组网等一系列优势,并被广泛用于国内外的新能源外送工程中。

近年来,MMC-HVDC系统从点对点结构逐步拓展至多端直流、直流电网、高压交流电网异步互联等复杂场景中。例如我国在广东南澳和浙江舟山投运的MMC-HVDC工程均采用风电场群的多端互联结构。在多端系统中,不同风场互为支撑,可一定程度上缓解新能源的出力波动。2020年6月落户张北的世界首个柔性直流电网示范项目通过四端环网实现了风电、光伏、储能的联合发电,其环网结构有效提升了直流输电的可靠性与灵活性。此外,在2016年与2018年分别建成的云南-鲁西HVDC工程和渝鄂HVDC工程中,通过MMC的背靠背连接实现了两个高压交流电网的异步互联,提升供电可靠性。可以看到,MMC-HVDC正逐步向多端化、网孔化转变,并与传统高压交流输电网、中压交流配电网相互融合,交直流混联与电力电子化将成为未来电力系统的必然趋势。

得益于MMC等电力电子换流装置的全控特征,电网调控的灵活性与响应速度均有了跨越性提升。但与此同时,电力电子化电力系统的稳定性隐患也逐步显露[1-2]。在传统电网中,同步发电机通常具有较大的时间常数和较低的控制带宽,中高频扰动信号在控制系统内被快速衰减,因此一般不会与小时间常数的电网线路引发谐振。与同步机相比,半导体器件的高速开关动作大幅拓宽了电力电子换流器的可控频带,控制作用呈现多时间尺度特征,如图1所示。高带宽的电力电子换流器极易与线路阻抗以及其他换流器相互作用并引发失稳振荡,产生的振荡谐波不仅恶化了电网的供电质量,甚至可能不断传播、放大并触发故障保护,导致系统闭锁停运。值得注意的是,不同于开关动作所引入的固定频率谐波,上述振荡谐波从数赫兹到数千赫兹皆有分布,亦被称为“宽频振荡”,其与换流器的控制策略、控制参数、拓扑结构、元件参数等多方面因素均有关联[3-4]。随着MMC-HVDC工程容量和数量的不断增加,供电稳定性受到严重威胁。

图1 电力系统中的控制带宽分布

近年来,国内外许多学者对MMC的精确建模理论和稳定性分析方法展开了一系列探索,本文旨在对这些方法和研究现状进行归纳梳理。

1 基于非线性时变模型的大信号分析

稳定性分析方法按照所采用的数学模型可划分为非线性时变与线性定常两大类,其中对线性定常系统的研究又可细化为基于状态空间模型的特征值分析和基于传递函数的奈奎斯特判据分析。

在开关器件动作和非线性控制环节的影响下,任何电力电子装置本质上都属于非线性时变系统。从MMC的物理机理出发,联立实际电路的全部电压、电流方程,即可获得MMC的非线性时变详细模型。然而包含MMC全部动态特性的模型异常复杂,实际中需要通过适当的近似处理来降低模型阶次。文献[5]提出的详细模型忽略了开关动作在寄生电容、电感上产生的暂态响应,但保留了MMC桥臂中的模块化结构,可用于子模块内部电压、电流特性的研究,例如模块故障保护、模块电压平衡控制等。考虑到MMC同一桥臂内的子模块电容电压在正常运行时相差无几,文献[6]提出MMC的桥臂平均模型,直接采用一个平均子模块代替了整个桥臂,避免了模块数目过多带来的复杂性,且能准确反映桥臂间的环流特性与电容电压的平均波动,可用于环流控制、相间及臂间电容电压平衡控制等绝大部分拓扑层面研究,是应用最为广泛的MMC非线性时变模型。从系统层面来看,MMC的研究重点集中于交、直流端口的电压和电流外特性,此时电容电压波动和内部环流成为次要因素,故可以进一步忽略电容电压谐波与桥臂结构,对MMC整体进行平均化处理,得到MMC的换流器平均模型[7]。

对于上述非线性时变模型,所能采用的稳定性分析方法为Lyapunov在1892年提出的Lyapunov直接法。该方法以“稳定系统动态变化过程中的能量始终单调减少”为依据,通过建立系统的能量函数来判断非线性系统的稳定性,具有理论严谨、判断准确、物理意义直观等优点。然而该方法中最为关键的能量函数选取则依赖经验和试错,尚无通用方法,因此对于MMC这样电路结构复杂、控制策略繁多的高阶系统很难采用。特别是在研究多个MMC构成的交直流混联系统时,这一问题更加突出。此外,在高阶系统研究中,Lyapunov直接法一般仅定性地判断一个系统是否稳定,而难以指导MMC电路参数及控制策略的设计[8]。鉴于上述局限性,MMC的非线性时变模型很少用于宽频振荡的理论分析,而多见于数值仿真验证中。

2 基于线性定常模型的小信号分析

研究稳定性的另一类思路是Lyapunov间接法,即先将系统的非线性时变模型转化为线性定常模型后,再通过成熟的线性系统理论进行分析。该方法虽仅能判断系统在某一平衡点(稳态工作点)邻域内的小信号稳定性,但却是整个系统稳定的必要条件。诸多研究表明,实际工程中的宽频振荡多属于小信号稳定性问题,即系统在某个稳态工作点处由于输出功率、硬件或控制器参数设置不当而逐渐振荡失稳。因此,基于线性定常模型的小信号分析法在宽频振荡问题中获得大量关注。

将换流器的线性定常模型整理为状态空间表达式,即可通过特征值来研究换流器的稳定性。除稳定性外,状态空间还能提供可控性、可观性、主导模态、稳定裕度、振荡频率以及参与因子等丰富信息[9],如图2所示。然而,基于特征值的分析方法在MMC-HVDC系统中仍有较大局限性。一方面,建立状态方程需要首先获知整个系统的所有软、硬件参数和网架结构,属于白箱模型[10]。对于传统交流电力系统,发电机、变压器均可根据铭牌提供的参数直接近似为简单的阻感元件,获取状态方程并不困难。但MMC的电路结构与控制策略远比同步机复杂,再加上设备供应商的技术保密措施,仅凭简单的硬件参数难以准确构建模型。此外,单台MMC的状态方程已经十分复杂,当应用至系统层面的稳定性研究时将面临“维数灾”,限制了该方法的工程应用。从分析过程来看,复杂系统的特征值主要依赖数值计算和作图观察等方式开展研究,所得到的分析规律往往只针对某一特定工况有效,难以给出MMC参数设计的通用性结论。

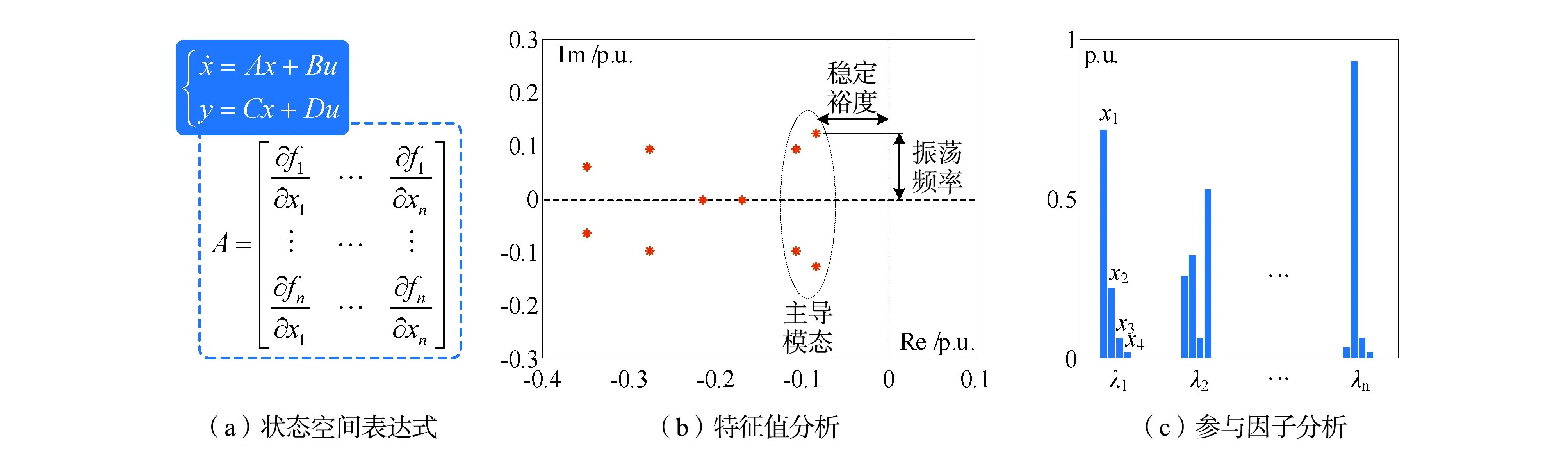
图2 基于状态空间的分析方法

传递函数是研究线性系统稳定性的另一种常用手段,可反映系统指定输入、输出信号之间的动态关系,不仅能通过线性定常模型进行理论推导,在工程中还可以直接扫频检测。借助传递函数的频率响应曲线,能够对稳定裕度、控制带宽、谐振峰值、稳态误差等多项性能指标进行分析,应用十分广泛。根据输入、输出信号的选择方式,可进一步将传递函数分为控制回路传函与端口阻抗两种类型。

当换流器接入电网后,电网将作为控制回路的一部分包含在模型中,因此控制回路传函能够反映换流器的并网稳定性[11]。然而,控制传函的扫频检测需深入换流器内部,且仅以单台设备为研究对象,不利于系统层面的稳定性分析。另一方面,并网端口的电压与电流能够反映换流器与电网间的全部交互信息。阻抗作为端口电流、电压之间的传递函数,无需深入换流器内部即可完成扫频检测,降低了对换流器参数的依赖[12]。凭借检测的独立性,可以分别对换流器与电网阻抗提出相应的稳定性指标、研究独立的稳控措施。在获取系统各节点的阻抗模型并聚合简化之后,并网点两侧的阻抗之比可等效为开环传函,继而通过奈奎斯特判据进行分析,如图3所示。除此之外,阻抗模型具有清晰的物理意义,其频率特性曲线能够直观反映控制策略的作用频段及控制效果,为振荡风险频段定位和抑制提供设计依据。基于上述优势,阻抗模型被广泛用于系统层面的换流器并网稳定性研究中。

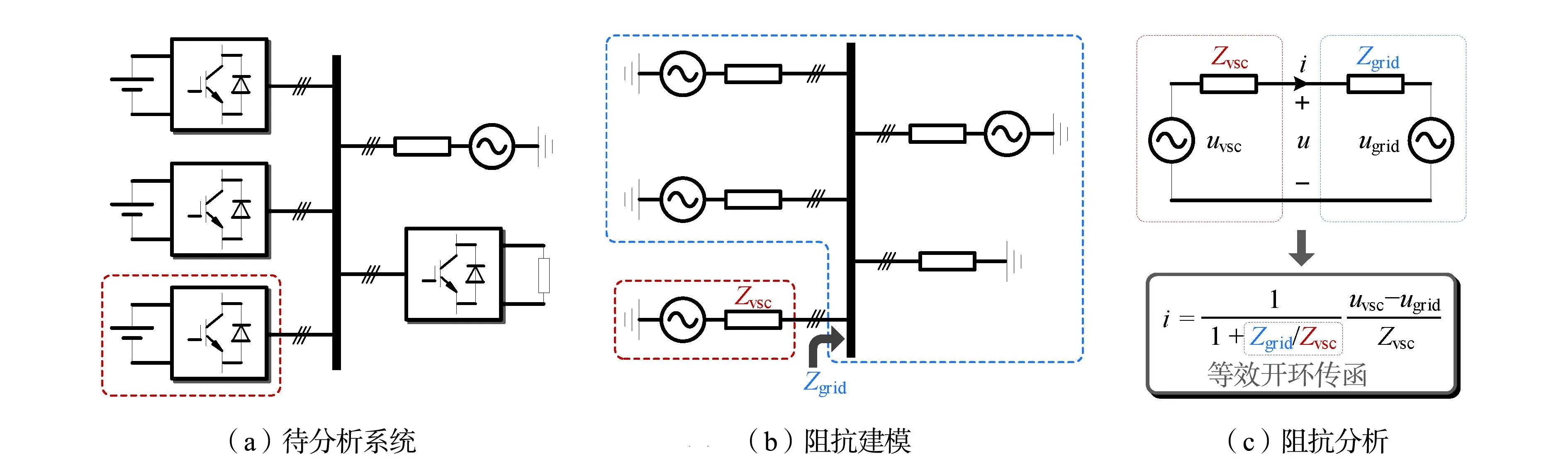
图3 阻抗分析法

3 阻抗建模及其稳定性分析方法

获取线性定常模型是开展阻抗分析的第一步,为此需要对MMC的非线性时变模型进行线性化和定常化。事实上,电力电子换流器的数学建模无一不是围绕其定常化展开。根据换流器所含谐波成分的不同,可分为直流斩波拓扑、单谐波拓扑和多谐波拓扑,分别衍生出不同的定常化思路。

阻抗判据最早由Middlebrook教授于1976年提出[11],用于研究直流斩波器与输入滤波器相连时的稳定性问题,并在开关电源领域得到大量应用。开关谐波是Buck、Boost等直流斩波类换流器的主要时变成分。考虑到开关谐波频率通常远高于换流器的控制带宽,对换流器的动态性能影响甚微,因此直接忽略开关谐波即可实现模型的定常化。

新能源发电中常见的两、三电平换流器属于单谐波拓扑。此类拓扑的输出电压中除了开关谐波外还包括基频成分,仅忽略开关谐波仍无法实现整个模型的定常化。针对换流器中的基频成分,目前普遍采用dq同步坐标系与静止坐标系两种建模方法。将基频信号转化至dq坐标系后表示为直流量,是单谐波拓扑实现定常化最直接的方法。然而在dq坐标系下,系统变量之间存在耦合,导致模型需采用二维矩阵形式[15-16],成为多输入-多输出(Multiple Input Multiple Output,MIMO)系统,原本针对单输入-单输出(Single Input Single Output,SISO)系统的奈奎斯特判据不再适用。面向MIMO系统的稳定性判据最早由英国曼彻斯特理工大学的MacFarlane教授提出[17],称为广义奈奎斯特判据(Generalized Nyquist Criterion,GNC),并在文献[18]中得到严格数学证明。基于GNC,Belkhayat将阻抗分析法拓展至交流并网换流器,利用dq阻抗模型初步开展了电力系统的稳定性分析[15]。随后,Harnefors[19]与Wen[20]分别将PLL和dq电流解耦项、功率外环等控制策略考虑到模型中,进一步完善了两电平换流器的dq阻抗建模方法。

另一方面,Harnefors在两电平换流器建模过程中引入无线通信中广泛使用的复信号概念[22],通过对称分量法将正、负序信号表示为一对反向旋转的复空间向量,获得换流器的复阻抗模型[23]。在该模型中,时间变量以复指数形式显现并能方便地从信号中分离,继而实现定常化。伦斯勒理工的孙建教授则直接从频域出发,基于描述函数思想分析了换流器在正、负序扰动下的频率响应,获得序阻抗模型[24-25]。实际上,复阻抗中成对出现的旋转向量恰好对应着序阻抗中的正、负序分量,因此复阻抗与序阻抗本质是同一种模型。早期的序阻抗模型忽略了正、负序扰动间的耦合作用,其模型呈现为SISO形式,不同相序扰动之间的独立性一度被视为序阻抗的独特优势[12,21]。然而这一优势仅限于平衡对称系统[22-23],当采用dq增益非对称的控制策略时,正、负序之间不再独立。Bakhshizadeh在文献[24]的基础上揭示了这一耦合现象,并将序阻抗改进为二维矩阵形式[26]。与dq阻抗类似,序阻抗矩阵亦需采用GNC进行稳定性分析。为了避免使用GNC,张琛等人[27]对序阻抗矩阵进行等效变换,再次转化到一维形式,提出一种融合全部阻抗矩阵元素的SISO序阻抗,可直接使用传统的奈奎斯特判据。孙建在文献[28]与文献[29]中进一步分析了这种SISO序阻抗与电网阻抗间的耦合效应。除此之外,为了研究交直流混联系统的稳定性,Shah针对两电平换流器提出一种能够反映交、直流系统耦合的三维序阻抗矩阵模型[30-31],与二维序阻抗矩阵和SISO序阻抗模型具有相同的稳定性[32]。

由于换流器的控制策略大多直接构建于dq坐标系下,dq阻抗的建模过程更为便捷。然而该模型侧重于反映d、q信号之间的耦合,与换流器的实际物理现象难以关联。与dq阻抗相比,建立在静止坐标系下的序阻抗能直观体现换流器的频率耦合,与实际工程中频繁出现的镜像频率耦合现象一致(即谐波频率关于基频镜像对称),具有十分清晰的物理含义[28]。长期以来,关于dq阻抗与序阻抗模型的研究各自独立开展,但两者实际上都是对相同换流器的数学描述,因此必然具有等价性。挪威科技大学Rygg与奥尔堡大学王雄飞教授先后通过线性代数证明了dq阻抗与序阻抗具有相同的稳定性,并给出了两种模型的等价转换矩阵[33-35]。文献[36]则在此基础上进一步辨析了dq坐标系、静止坐标系、实数域、复数域的数学概念,展示了不同阻抗间的完整转化关系,如图4所示。

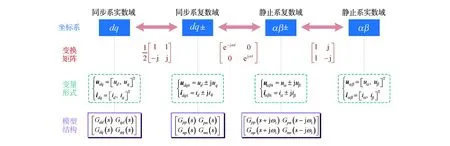
图4 dq同步坐标系与静止坐标系模型之间的等价转换关系

与两电平换流器相比,MMC具有更复杂的谐波特性,其内部电容电压、电感电流和调制波中的交流分量反复耦合,导致模型变量中不仅包含直流和基频成分,还存在二次、三次等谐波,因此MMC属于一种多谐波拓扑[37]。为实现MMC模型定常化,最简单的思路是直接忽略内部谐波,将MMC按照传统两电平换流器的建模方式进行处理[38-39]。然而内部谐波会显著影响MMC的动态过程,近似模型的分析结论与实际MMC之间存在较大偏差。为了提升分析精度,势必要将MMC的主要谐波都包含在模型中。谐波状态空间(Harmomnic State Space,HSS)理论作为一种多谐波建模方法,在MMC建模领域中备受关注。该理论指出:对于具有周期时变性的系统模型,可通过傅里叶级数将其模型从时域转化至频域,使各次谐波成分均能表示为不随时间变化的傅里叶系数,从而实现定常化。HSS理论经Wereley[40-42]提出后,很快被Rico[43-44]、Mollerstedt[45]、Love[46]等人推广至电气领域,分别用于研究晶闸管投切电抗器、铁路牵引单相供电系统以及两电平换流器的开关谐波问题。鉴于HSS在多谐波拓扑建模的优势,上海交通大学吕敬教授率先将其用于MMC-HVDC风电汇集系统,在忽略序间耦合的假设条件下构建了MMC的SISO序阻抗模型[47-49]。与此同时,孙建教授采用基于描述函数思想的建模方法也获得了MMC的序阻抗[50-51],其定常化原理与HSS一致,都是通过傅里叶级数将时变谐波转化至频域,因此可视为同一种建模方法。文献[52-53]借鉴两电平换流器的阻抗研究结论,先后建立了MMC交流侧的二维序阻抗模型,利用矩阵的副对角元素刻画正、负序之间的耦合关系。文献[54]则进一步提出了MMC阻抗矩阵的三维结构,将交、直流系统间的耦合也纳入模型中。另一方面,Jamshidifar[55]、鲁晓军[56]等则是将dq坐标系建模方法拓展为多dq坐标系,完成MMC的定常化建模。与两电平换流器建模方法相似,HSS与多dq坐标系模型仅仅是频域下的变量形式不同,其数学本质依然等价。其中,HSS方法在频域中采用傅里叶级数的指数形式(复系数),而dq坐标系则是直接采用了三角函数(实系数),两类模型可通过欧拉公式相互转化[57]。目前,基于HSS或多dq坐标系的谐波定常化思路已被广泛采用。

在阻抗特性分析方面,MMC内部耦合谐波的分布规律与扰动电压位置、相序均密切相关,且控制系统将对各次谐波呈现出不同的增益,导致MMC阻抗模型的数学形式十分复杂。文献[51]初步探讨了MMC电容电压中的耦合现象,揭示了不同电容电压谐波间的耦合规律。文献[58]在此基础上,提出一种基于相序选择矩阵和移频矩阵的MMC建模方法,统一了闭环控制下MMC交、直流回路的建模过程,涵盖了柔直工程中常见的定功率、定交流电压、定直流电压等控制模式,并能便捷地拓展至其他控制结构,具有较强通用性。该模型不仅能够直观反映MMC内部的频率、相序耦合,亦能体现MMC所接交、直流电网之间的耦合关系。

4 MMC模型简化

谐波耦合不可避免地加剧了MMC模型的复杂性。MMC内部的无穷次谐波表明其阻抗模型必然呈现为无穷维的矩阵形式,在实际应用前必须进行降阶简化。

常见的模型降阶理论主要针对状态空间模型提出,例如模态截断法[59]、奇异摄动法[60]、平衡理论[61]等。这些方法的核心思想是通过保稳数学变换移除一部分低时间尺度的非主导特征值来简化模型。然而经数学变换后的状态变量与真实系统之间存在差异,失去了变量原本的物理意义。除此之外,状态空间模型的固有问题也限制了这类简化方法在MMC-HVDC系统中的推广。对于MMC的阻抗模型,目前所用的简化依据主要基于感性经验或仿真观察。由于MMC的内部谐波幅值一般都随着频率升高而降低,大部分文献均采取直接忽略高次谐波的方法简化模型,通常仅保留前两次或前三次稳态谐波[47-57]。然而,这种近似方法不具有通用性。为解决上述问题,文献[67]提出一种基于信号流图前向增益的MMC谐波量化估计方法,为无穷维阻抗矩阵的截断降阶提供了理论依据。

除了截断高次谐波外,还可以根据阻抗元素的数学特征简化模型结构。文献[31]与文献[62]揭示了两电平换流器模型的共轭对称性,有助于简化二维阻抗矩阵元素的求取过程。文献[63-66]则通过分析阻抗传函,相继给出了阻抗与参考相位之间的对应关系,方便了模型参考系变化后阻抗附加相位的计算。文献[27]通过将二维阻抗矩阵转化为SISO阻抗,降低了稳定性的分析难度。文献[67]将两电平换流器的阻抗特性推广至MMC,采用信号流图揭示了MMC无穷维阻抗元素之间的共轭对称性,提出元素对称关系与相位偏移量的直观判断方法,简化了矩阵元素的求取过程,并建立MMC多维阻抗矩阵模型与SISO阻抗模型等价转换公式,从而避免在稳定性分析中使用广义奈奎斯特判据。

5 结论与展望

目前,针对MMC的建模方法、稳定机理、内部耦合、模型简化降阶等方面的研究趋近成熟甚至饱和。所建模型的精度已经足以针对1～5 000 Hz频率范围内的振荡现象展开研究。然而现有研究对稳定性分析和振荡抑制策略的探索还远不充分,以至于振荡事故至今仍在HVDC工程中反复出现。如何使用所建立的阻抗模型对振荡问题进行分析,进而提出普适有效的稳定控制策略是当前宽频振荡问题研究的关键。一方面,未来的交直流混联电力系统将向网孔化、多端化逐步发展,亟待发展多节点、多网孔的系统级阻抗网络稳定性分析和稳定控制方法;另一方面,面对复杂的阻抗网络,仅依赖单个换流站的参数优化将难以实现整个系统稳定裕度的高效提升,系统的全局稳定性需要多个换流站共同参与。考虑到系统复杂性,面向数据驱动的多站点协同振荡抑制技术也可能成为未来的研究方向之一。