输电导线融冰体系脱冰振动数学模型及振动试验

陈 彪,李春城,刘 斐,韩兆冰,侯笑天

(1.国网吉林省送变电工程有限公司,吉林 长春 130000;2.国网齐齐哈尔供电公司经济技术研究所,黑龙江 齐齐哈尔 161000;3.国网浙江省电力有限公司建设分公司,浙江 杭州 310000;4.东北电力大学建筑工程学院,吉林 吉林 132000;5.吉林省输电工程安全技术工程实验室,吉林 吉林 132000)

0 引 言

直流融冰技术是最为成熟的融冰技术之一,2008年冰灾后,融冰装置在开发与实践实施方面取得了长足的进步[1-3],现阶段直流融冰技术在电网融冰中应用最为广泛,其基本原理是利用输电线路短路时电流的热效应,将输电线路上的覆冰融化。输电塔融冰体系是短接作业的主要装置,由悬臂组合机构和短接导线组成,其中悬臂组合机构是融冰作业线路短接时主要动作部位,由悬臂和支柱绝缘子组成。融冰过程中,悬臂组合机构上的覆冰也会脱落,脱冰导致悬臂组合机构发生振动、在稳定性、可靠性、绝缘安全性等方面产生极大影响[4-8]。

在直流融冰电源侧装置研究方面,学者们分别从电压互感器、模块化多电平换流器、整流变压器及设备内部元件改进等方面对直流融冰电源侧设备进行了调整和改进,使其更高效、灵活[9-11]。余轶等人提出一种新型直流融冰等效负载设备并给出试验方法[12];蓝磊等人则对余轶提出的方法加以运用和证明[13-14]。针对结构在覆冰脱落冲击作用下的动力响应,国内外学者主要在理论研究、仿真分析、试验测试三个方面展开研究。在理论方面,现阶段结构脱冰振动公式推导有拉格朗日方程和利用达朗贝尔原理进行振动方程的推导两种方法,前者相对简单,仅需考虑系统动能、势能及广义坐标,大大简化了推导过程,因此有众多学者采用,但研究内容略有不同。在仿真研究方面,黄桂灶建立了模拟导线脱冰的缩比模型,对不同档导线脱冰的相互影响进行了仿真分析[15];祝贺开展了高压输电线路脱冰动力响应的仿真分析,研究风攻角、风速及冰厚等参数对导线脱冰最大动张力的影响[16];楼文娟等人通过风洞试验获得了不同厚度覆冰导线的气动力系数[17];王黎明和晏致涛更偏重于探讨仿真分析时临界条件对结构脱冰振动的影响,进行结构脱冰振动有限元分析时考虑了覆冰破坏准则,使分析结果更加的准确、分析工况更加丰富[18-19]。在结构脱冰振动试验研究方面,国内外很多学者利用集中荷载法进行结构脱冰振动试验,通过在试验结构上按一定规律悬挂重物并根据试验工况逐步释放重物来实现覆冰脱落的模拟,分别测量结构脱冰后位移及力的变化以研究脱冰振动对结构的影响[20-23]。

结构脱冰振动研究考虑了不同覆冰厚度、脱冰率等脱冰工况及结构的自身属性参数,得到了大量覆冰脱落导致结构振动的研究成果。但仍存在以下问题:现有结构脱冰振动研究对象均以长距离、大跨度、挂点强度大的架空导线为主,对于悬臂组合机构脱冰振动研究较少,不能直接适用于融冰体系脱冰振动这一类情况,因此需开展输电塔融冰体系脱冰振动特性分析及试验研究。

1 融冰体系脱冰振动数学模型及求解

基于拉格朗日方程并结合假设模态法,考虑不同脱冰工况、参数属性及振动方向、结构内部耦合关系等,建立融冰体系短接导线和悬臂组合机构脱冰振动数学模型如公式(1)所示。

(1)

经分析推导得到融冰体系悬臂组合机构的总势能表达式、总动能表达式和耗散函数表达式,将上述各式代入拉格朗日方程中,得到融冰体系悬臂组合机构脱冰振动数学模型。

融冰体系悬臂组合机构脱冰振动位移数学模型表达式为

(2)

公式(2)中积分获得各项系数具体表达式和参数,包含悬臂组合机构覆冰厚度、脱冰率、阻尼比、长度、材料属性等参数,以上参数的改变将会导致悬臂组合机构脱冰振动位移情况发生变化,利用Matlab软件编程求解数学模型,在确定模拟时间和步长并代入不同覆冰厚度、脱冰率、材料属性等工况条件后,得到悬臂组合机构脱冰振动时位移随时间变化情况。

融冰体系悬臂组合机构脱冰振动过程中应力数学模型表达式

(3)

将利用悬臂组合机构脱冰振动位移数学模型得到的端点广义位移和所求应力点的水平坐标代入公式(3)中,求得悬臂组合机构在脱冰振动时的应力时程曲线。

同时考虑方程求解精度和计算繁琐程度,在Matlab软件中编写改进欧拉法求解融冰体系脱冰振动数学模型程序,给定工况参数和初始条件,计算得出融冰体系脱冰振动时各点随时间变化的广义位移,进而求解融冰体系脱冰振动数学模型。

在利用改进欧拉法对融冰体系脱冰振动数学模型求解前,需先将其进行降阶处理,降阶为一阶微分方程组,随后采用改进欧拉法对其进行求解,N等分区间,设定步长h=(b-a)/N。则积分形式为

(4)

为提高精度,采取梯形公式来计算公式(4)右端积分,经过迭代和趋近,将yn+1作为y(xn+1)的近似值。

将模型求解得出的广义位移代入实际位移、应力表达式,进一步得到融冰体系悬臂组合机构脱冰振动时的实际位移、应力时程曲线。

在Matlab软件中采用改进欧拉法求解数学模型。悬臂组合机构中支柱绝缘子长为0.3 m,悬臂为外径60 mm、内径30 mm、长4 m的铝制长管。得到融冰体系分别在10、20、30、40 mm覆冰厚度下完全脱冰时悬臂端部竖向位移和根部上表面正应力时程曲线如图1所示。

图1 不同覆冰厚度下悬臂组合机构脱冰振动时程曲线

根据数学模型计算结果,融冰体系在10、20、30和40 mm覆冰厚度下完全脱冰时,悬臂端部竖向位移最大值分别为0.047、0.084、0.132、0.188 m,悬臂根部上表面正应力最大变化幅值分别为14.852、27.685、43.399、61.915 N/mm2。

2 融冰体系悬臂组合机构脱冰振动仿真分析

采用Solidworks软件建立与数学模型算例中相同尺寸参数的融冰体系模型并导入ANSYS有限元仿真软件中,定义材料属性与数学模型计算中材料属性相同。

为满足计算精度要求的同时提升计算效率,在网格划分方面,采用自适应网格划分法划分网格。为保证仿真模型模态分析、脱冰瞬态分析的正确性,添加自重和覆冰荷载,经仿真软件迭代调整,使其满足导线覆冰后的初始状态,从而真实反映导线覆冰时的实际情况。建立的融冰体系有限元仿真模型如图2所示。

图2 融冰体系有限元模型

在仿真软件中求解仿真模型,各属性参数及脱冰工况均与数学模型求解时所设定的参数条件完全相同,分别求取融冰体系在10、20、30、40 mm覆冰厚度下完全脱冰时悬臂端部竖向位移和根部上表面正应力时程曲线如图3所示。

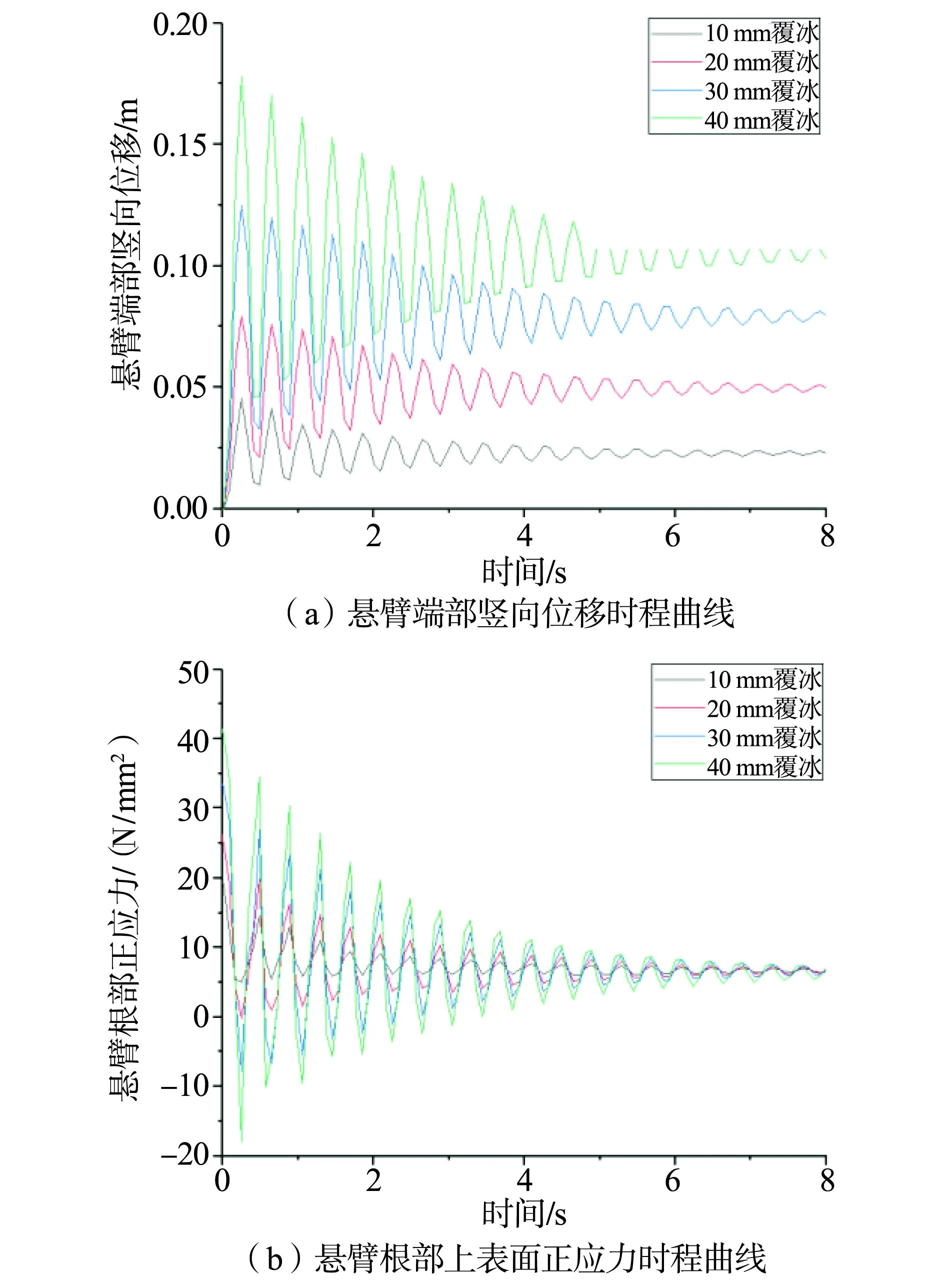
图3 不同覆冰厚度下悬臂组合机构脱冰振动时程曲线

由图3可知,提取与数学模型计算算例同工况条件下融冰体系脱冰振动有限元仿真分析结果,在10、20、30、40 mm四种覆冰厚度下完全脱冰时,悬臂端部竖向位移最大值分别为0.046、0.079、0.125、0.178 m,悬臂根部上表面正应力最大变化幅值分别为14.346、26.458、41.394、59.306 N/mm2。

建立与数学模型计算算例边界条件和属性参数完全相同的ANSYS有限元仿真分析模型,在相同脱冰工况下,将计算算例结果与同参数条件的仿真模型有限元分析结果作对比,融冰体系脱冰振动时悬臂组合机构端部位移及根部上表面应力最大相对误差分别为5.89%和4.62%,证明了建立数学模型时所作假设的合理性及数学模型的准确性。

3 悬臂组合机构脱冰振动特性

基于建立的悬臂组合机构脱冰振动数学模型,通过调整数学模型中脱冰率、覆冰厚度、阻尼比及悬臂材料属性、臂长等参数实现不同工况的模拟,并利用Matlab软件编程对其求解。提取受脱冰振动影响最大的悬臂端部位移、根部正应力时程曲线数据并进行分析,总结悬臂组合机构脱冰振动特性。

3.1 不同脱冰工况下悬臂组合机构脱冰振动特性

3.1.1 不同脱冰率下悬臂组合机构脱冰振动特性

采用控制变量法,设定支柱绝缘子长为0.3 m,悬臂长为4 m,阻尼比为0.02,在覆冰厚度为40 mm的重覆冰工况下,通过调整脱冰率参数为25%、50%、75%、100%,分别求解计算悬臂组合机构脱冰振动数学模型,得到脱冰振动时悬臂端部竖向位移和根部上表面正应力时程曲线如图4所示。

图4 不同脱冰率下悬臂组合机构脱冰振动时程曲线

由图4可知,在25%、50%、75%、100%四种脱冰率下,悬臂端部竖向位移最大值分别为0.080、0.116、0.152和0.188,悬臂根部上表面正应力最大变化幅值分别为26.371、38.17、50.064、61.915 N/mm2。分析以上数据得到:随着脱冰率的逐渐增大,脱冰导致的悬臂端部竖向位移和根部上表面正应力变化幅值也随之增大;在脱冰率大于75%时,悬臂根部上表面正应力出现负值,说明此时悬臂组合机构振动发生回弹,超过水平位置。同时,因脱冰率越大则悬臂与覆冰的整体质量越小,故振动频率也随脱冰率的增大而略微增加。待振动结束时,悬臂端部竖向位移最终值与脱冰率成正比、根部正应力最终值与脱冰率成反比,其原因是由于振动结束后悬臂组合机构将回到静力平衡状态,脱冰率越大悬臂与覆冰质量之和越小,则挠度越小,悬臂根部所受到的正应力也就越小。

3.1.2 不同覆冰厚度下悬臂组合机构脱冰振动特性

在悬臂组合机构外形尺寸、阻尼比和材料属性相同的情况下,仅调整覆冰厚度,得到在10、20、30、40 mm四种不同覆冰厚度工况下完全脱冰时悬臂端部竖向位移和根部上表面正应力时程曲线如图5所示。

图5 不同覆冰厚度下悬臂组合机构脱冰振动时程曲线

由图5可知,分析不同覆冰厚度下完全脱冰时悬臂组合机构位移、应力时程计算结果。在10、20、30、40 mm四种覆冰厚度下完全脱冰时,悬臂端部竖向位移最大值分别为0.047、0.084、0.132、0.188 m,悬臂根部上表面正应力最大变化幅值分别为14.852、27.685、43.399、61.915 N/mm2。因悬臂脱冰前后位置差及相同脱冰率时的脱冰量均随着覆冰厚度的增加逐渐增大,故悬臂脱冰时端部竖向位移和根部上表面应力变化幅值也随之增大;当覆冰厚度超过20 mm后,悬臂完全脱冰时上表面根部正应力产生负值,表明发生回弹现象。同时,不同覆冰厚度下,脱冰振动频率及脱冰振动完成后悬臂根部正应力值均基本一致,其原因是完全脱冰时振动本体仅为悬臂组合机构自身,其根部正应力、振动频率均只与其本身性质有关,故图像变化情况与实际相符。

在分析不同覆冰率下悬臂组合机构完全脱冰工况的基础上,利用数学模型进一步计算多组不同覆冰厚度与脱冰率的组合工况,并采用Matlab软件求解悬臂端部竖向位移和根部上表面正应力,提取出各工况下最大位移和正应力变化最大幅值数据如图6所示。

贵州省平塘县是一个以农业为主而水利工程相对滞后的农业县。2012年7月16日，在平塘县50年一遇洪灾发生过程中，由于预警及时，在洪水到来之前，提前转移了可能受洪水淹没的群众和财物，大大地降低了洪涝灾害造成的损失，山洪灾害非工程措施在本次洪灾中发挥了重要的防洪减灾作用。

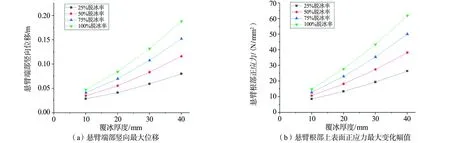
图6 不同覆冰厚度悬臂组合机构脱冰振动最大幅值变化图

由图6可知,对比分析不同覆冰厚度、同一脱冰率下的悬臂脱冰振动变化情况。随着覆冰厚度的增加,相同脱冰率下悬臂端部竖向最大位移变化率和根部上表面正应力最大幅值变化率也逐渐增大,其原因是悬臂组合机构覆冰厚度与覆冰质量为非线性关系,即实际覆冰质量增量高于覆冰厚度增量线性对应的覆冰质量增量,故产生竖向最大位移和正应力最大变化幅值的变化率逐渐增大的情况。同时,在四种不同覆冰厚度的工况下,悬臂组合机构脱冰振动悬臂根部正应力变化幅值与端部竖向最大位移变化趋势基本一致,成正比关系。

3.2 不同阻尼比下悬臂组合机构脱冰振动特性

阻尼的不同将直接影响悬臂组合机构脱冰振动衰减速度。分析不同阻尼比对悬臂组合机构脱冰振动的影响,阻尼比0、0.01、0.02、0.03下悬臂端部竖向位移和根部上表面正应力脱冰振动时程曲线如图7所示。

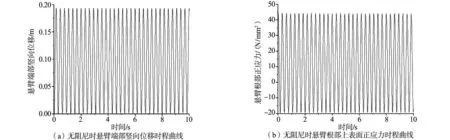
图7 不同阻尼比下悬臂组合机构脱冰振动时程曲线

由图7可知,分析不同阻尼比下悬臂组合机构脱冰振动时程曲线:悬臂组合机构阻尼比越大,能量衰减的就越快,振幅衰减系数也越大,悬臂组合机构也更快的趋于平衡。在阻尼比从0.01增至0.03时,结构振动结束趋于稳定时长由18 s减少至7 s,因此阻尼比的增加将有效抑制脱冰振动对悬臂组合机构的影响。在无阻尼时,悬臂端部脱冰振动竖向位移和根部上表面水平应力在中心轴线上下摆动,无衰减趋势,符合实际情况,证明数学模型中阻尼比因素的有效性。

3.3 不同属性参数下悬臂组合机构脱冰振动特性

悬臂应具有良好的导电性以满足大电流通过的需求,但同时又需考虑质量因素,因此需要对不同材质悬臂受脱冰振动影响情况进行分析;针对不同塔型结构和实际需求,需对悬臂臂长进行适应性调整,故对不同臂长下悬臂组合机构脱冰振动特性进行分析。

3.3.1 不同材质下悬臂组合机构脱冰振动特性

选取导电性较好的铝和铜两种材质,利用Matlab软件分别对两种材质下悬臂组合机构脱冰振动情况进行分析。设定悬臂组合机构外形尺寸、阻尼比相同,仅调整材料属性参数,求取在材质为铝和铜的情况下完全脱冰时悬臂端部竖向位移和根部上表面正应力时程曲线如图8所示。

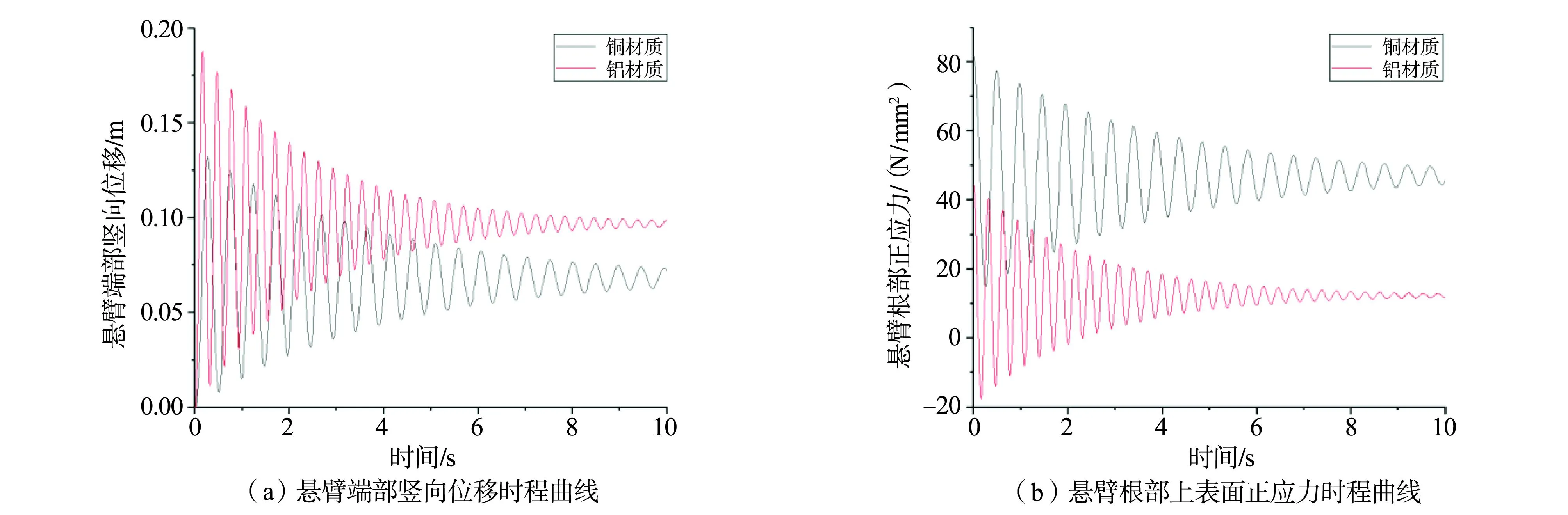
图8 不同材质下悬臂组合机构脱冰振动时程曲线

由图8可知,在铝和铜材质下完全脱冰时,悬臂端部竖向位移分别为0.188 m和0.138 m,悬臂根部上表面正应力最大变化幅值分别为61.915 N/mm2和69.643 N/mm2。在相同脱冰工况下,铝悬臂比铜悬臂竖向位移变化大但应力最大变化幅度小。在重覆冰情况下,铜悬臂根部上表面正应力始终为正值,不会发生回弹现象,而铝悬臂则有回弹现象发生。同时,铝悬臂振动频率也大于铜悬臂振动频率。其主要原因是铜的弹性模量虽为铝的1.5倍,但密度却为铜的3.3倍,故质量因素对振动影响更大,从而产生上述变化。因此铝悬臂虽相对较轻,但在同等覆冰条件下更易受脱冰振动影响。

3.3.2 不同臂长下悬臂组合机构脱冰振动特性

在悬臂组合机构材料属性参数、覆冰情况相同的条件下,仅调整悬臂长度为3、4、5 m,求取在不同臂长情况下完全脱冰时悬臂端部竖向位移和根部上表面正应力脱冰振动时程曲线如图9所示。

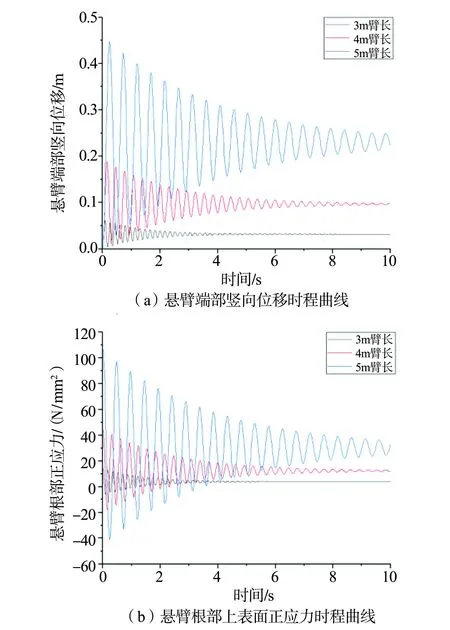
图9 不同臂长下悬臂组合机构脱冰振动时程曲线

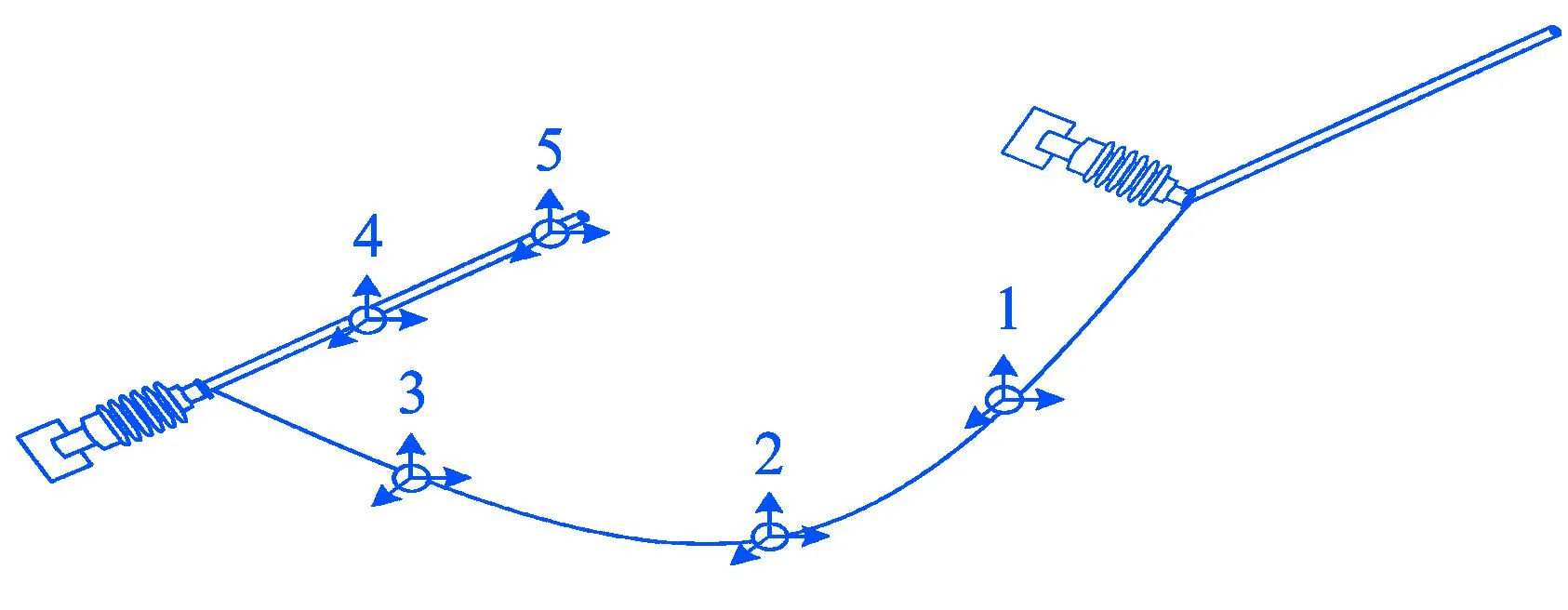
图10 监测点位布置图

图11 融冰体系悬臂机构及短接作业

由图9可知,在3、4、5 m三种臂长下完全脱冰时,悬臂端部竖向位移分别为0.062、0.188、0.448 m,悬臂根部上表面正应力最大变化幅值分别为20.296、61.915、147.46 N/mm2。随着臂长的增加,在完全脱冰时,悬臂端部竖向位移和根部上表面正应力变化幅值显著增加,但振动频率逐渐变慢。其主要原因是完全脱冰后,悬臂振动频率仅与悬臂自身性质有关,在弹性模量和密度相同的情况下,臂长越大则质量越大,故振动越慢。在振动过程中,臂长越短则越快趋于平衡,结构受脱冰振动的影响越小。在振动结束时,臂长越长,静止时刻端部竖向位移和根部上表面正应力越大,这也与悬臂越长则挠度越大、应力越大的实际情况相符。

4 融冰体系脱冰振动试验

在进行融冰作业时同步开展融冰体系脱冰振动试验测试,基于在线监测技术,利用振动、覆冰在线监测装置,采集融冰体系脱冰振动情况及覆冰厚度、气象条件等气象环境参数,提取分析悬臂组合机构端部(监测点4)的竖向位移时程数据。

融冰体系由悬臂组合机构和短接导线共同组成,悬臂组合机构主体由长3.7 m的空心铝管和长0.3 m的支柱绝缘子构成,材料属性参数如表1所示。

表1 融冰体系材料属性参数

进行融冰体系脱冰振动试验测试时,环境温度为-3 ℃,平均风速为2.9 m/s,等效覆冰厚度为13.4 mm。在以上气象条件和覆冰厚度下融冰体系完全脱冰,在振动监测系统中提取悬臂组合机构端部(监测点4)竖向位移时程数据如图12所示。

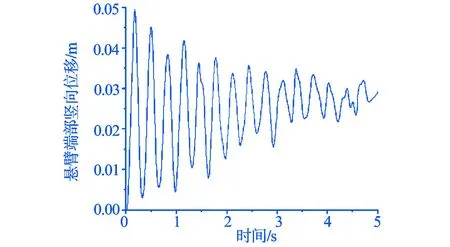
图12 试验测试悬臂端部(监测点4)竖向位移时程曲线

由图12可知,根据试验测试结果,融冰体系在13.4 mm覆冰厚度下完全脱冰时,悬臂组合机构端部(监测点4)竖向位移最大值为4.96 cm。

利用Matlab软件基于融冰体系脱冰振动位移数学模型,将表1中悬臂组合机构各项参数代入数学模型中,求取相同脱冰工况下的融冰体系脱冰振动位移时程曲线,提取对应于悬臂组合机构端部(监测点4)的竖向位移时程曲线如图13所示。

图13 模型计算悬臂端部(监测点4)竖向位移时程曲线

由图13可知,提取与试验测试同工况条件下融冰体系脱冰振动位移数学模型计算结果,在13.4 m覆冰厚度下完全脱冰时,悬臂组合机构端部(监测点4)竖向位移最大值为5.81 cm。将其与同脱冰工况及参数条件的试验测试结果进行比对,悬臂组合机构端部(监测点4)竖向位移变化最大值相对误差为17.14%。

5 结 论

以融冰体系为研究对象,采用理论推导、仿真分析及试验测试等方法,建立、求解并验证融冰体系脱冰振动位移、应力数学模型,分析各工况条件下融冰体系脱冰振动特性变化规律。得到以下结论:

1)通过分析数学模型参数,除单位长度覆冰情况(以脱冰率和覆冰厚度表征)及阻尼比对结构脱冰振动有影响外,悬臂组合机构各部分长度、材料属性参数、内部结构的耦合关系等因素均对融冰体系脱冰振动有直接影响。

2)脱冰振动导致的融冰体系位移、应力变化幅值随脱冰率和覆冰厚度的增加逐渐增大;相同脱冰率、不同覆冰厚度下融冰体系脱冰振动频率基本一致,但随着脱冰率的增大而略微增大。结构阻尼比的增加将有效加快振动衰减速度,当阻尼比由0.01升至0.03时,振动时间缩短约40%,故阻尼比的增加将加快振动幅值的降低,但对最大振动幅值的影响有限,因此通过合理增加阻尼能起到较好的减振作用。

3)融冰体系悬臂组合机构脱冰振动受材质和臂长影响显著。在材质影响方面,相同脱冰工况下,铝悬臂脱冰振动竖向位移和振动频率比铜悬臂更大且有回弹现象发生,但应力最大值和变化量小于铜悬臂。在臂长影响方面,随着臂长的增加,悬臂端部竖向位移和根部正应力变化量显著增加,但振动频率逐渐变慢。因此在悬臂长较长时,需利用悬臂组合机构脱冰振动位移数学模型进行位移核算,材质选择界限范围根据数学模型计算结果结合动静触头接触范围确定。