G可数紧空间

刘 丽

(宁德师范学院数理学院, 福建 宁德 352100)

序列的收敛性是数学中的一个基本概念．长期以来, 通常收敛概念的深化一直是拓扑学与分析学的一个有趣的研究方向, 如, 实分析中的统计收敛[1], 泛函分析中的几乎收敛[2]、理想收敛[3]等．近期, Lin等[4]引入了任意集合上的G-方法及G-收敛性, 讨论了拓扑空间中保持G-收敛映射与连续映射之间的关系, 引起了相关学者的关注[5-6]．在拓扑学中, 与序列相关的紧性主要有序列紧性及可数紧性等．笔者于2009 年研究了G-方法下的序列紧性[7]． Cakalli[8]在拓扑群中研究了G序列可数紧性.本文基于G-收敛性定义了一般空间中的G-可数紧性, 研究了其基本性质及其与相关空间的基本关系．

1 预备知识

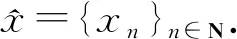
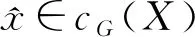
定义2[4]设G是拓扑空间X上的方法,A⊂X, 有

2) 若XA是X的G-闭集, 则称A为X的G-开集．

定义3设X是拓扑空间,G:cG(X)→X．

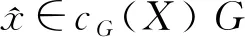
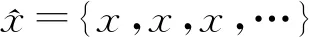
显然, 正则方法是点式方法．通过正则方法或子序列方法, 可以建立G-收敛与X中收敛序列的密切联系[4]．

定义4[4]设G是拓扑空间X的方法,A⊂X．若存在X中的G-开集U使得x∈U⊂A, 则称A为x∈X的G-邻域．

定义5[4]设G是拓扑空间X上的方法．若X中每一G-闭集是闭集, 则称X为G-序列空间．

定义6[7]设G是拓扑空间X上的方法．若X中任意序列有G-收敛的子序列, 则称X为G-序列紧空间．

对于文中未给出的定义或记号, 读者可从文献[4]、 [10]查阅．

若拓扑空间X的每一可数开覆盖具有有限子覆盖,则称X为可数紧空间[10]．可数紧性可用聚点的概念来描述．

引理1[11]对于拓扑空间X下述条件相互等价:

1)X是可数紧空间;

2)X中的每一序列有聚点;

3)X的每一无限集A存在ω聚点, 即存在x∈X使得x的任意邻域含有集A的无限个点．

鉴于在正则条件下“收敛序列是G-收敛序列”, 以及一些与G-收敛概念相关的拓扑空间的定义[4], “G-可数紧空间”至少满足:“正则或者其他条件下, 可数紧空间是G-可数紧空间”, 以及“G-序列紧空间是G-可数紧空间”．由引理1, 可以尝试从集合的“聚点”着手来定义G-可数紧空间．下面介绍G-收敛下聚点的定义与刻画.

定义7[9]设G是拓扑空间X的方法,x∈X,A⊂X．

1) 若对x的任意G-邻域U, 有U∩(A{x})≠φ, 则称x∈X为A的G-聚点．A的全体G-聚点之集称为A的G-导集, 记作AdG．

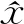
显然, 任意A⊂X, 则AG=A∪AdG[9]．

引理2[9]设G是拓扑空间X的方法,A⊂X．那么

1) (A′)G⊂AdG．

2) 若G是X上的子序列方法, 则(A′)G⊂Ad．

俗话说，树高千尺不忘根，创业致富不忘本。涂桑田稻田养虾成功后，被村党支部和村民兵评为“稻虾共作”致富标兵和产业脱贫致富明星。为了使乡邻共同养殖致富，他把自己的养虾技术和经验传授给乡邻。得知涂新旺、涂万田、陈新友等17户贫困户致富无门路，涂桑田就积极联系机械设备帮助他们对稻田养虾的低洼田进行改造，达到沟、渠、路配套。同时，涂桑田以自家农场为培训基地，组织贫困养虾户免费到基地参观学习。在育秧插秧和投放虾苗季节，涂桑田亲自到现场进行技术指导。全镇已有20多户贫困户开始稻田养虾，与桑田家庭农场结成了利益共同体。

3) 若X是G-序列空间, 则Ad⊂AdG．

4) 若X是G-Fr’echet空间则Ad⊂(A′)G．

Cakalli[8]在第一可数的拓扑群上定义了G-序列可数紧空间X(G-sequentially countably compact space): 若X中每一无限子集F至少含有一个G-序列聚点．因序列的G-收敛点不一定是由序列构成的集合的G-序列聚点, 故此条件下G-序列紧空间不一定是G-序列可数紧空间, 详见例4．此外, 正则条件下, 集合的ω聚点不一定是G-序列聚点, 例如, 在Arens空间X={0}∪N∪N2[11]中, 令G:cG(X)→X为通常的序列收敛, 则G是正则方法．此时,{0}是无限子集N的ω聚点但不是G-序列聚点．因此, 在正则条件下, 可数紧空间亦不一定是G-序列可数紧空间．根据上述分析, 本文从集合的G-聚点出发, 定义G-可数紧空间．

定义8设G是拓扑空间X的方法,F⊂X．若F中每一无限子集至少含有一个G-聚点, 则称F为X的G-可数紧子集．

下面讨论G-可数紧与可数紧子集的关系．

定理1设G是序列空间X上的正则方法．若F是X的可数紧子集, 则F是X的G-可数紧子集．

证明 若F是X的有限子集, 结论显然成立; 若F是X的无限子集, 任取F的无限子集A, 设A中每点互异, 若AdG=φ, 则任意a∈X,a∉AdG．由定义7, 存在a的G-邻域U使得U∩(A{a})=φ．因为G是序列空间X上的正则方法, 所以U是a的邻域且U∩(A{a})=φ, 于是a不是A的ω聚点．这与F是X的可数紧子集矛盾, 故AdG≠φ．由定义8,F是X的G-可数紧子集．

定理1中的正则方法条件不可省．

例1存在第一可数空间X及X上的非正则方法G, 使得X的某一可数紧子集不是G-可数紧的．

令X=[0,ω1], 赋予序拓扑．显然,X是第一可数的序列紧空间．

令A=[0,ω]．任意x∈X, 因N⊂A且{x}是点x的G-邻域, 此时N∩({x}x)=φ, 故NdG=φ,于是无限子集N无G-聚点．因而A是X的可数紧子集但不是G-可数紧的．

定理2设G是拓扑空间X上的子序列方法．若F是X的G-可数紧子集, 则F是X的可数紧子集．

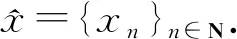
定理2中的子序列方法不可省．

例2存在序列空间X及X上的非子序列方法, 使得X的某一G-可数紧子集不是可数紧的．

令X=R, 赋予通常拓扑, 则X是序列空间．

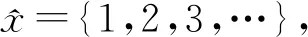
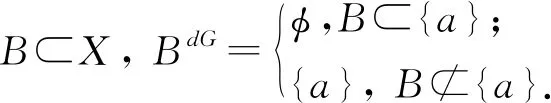
因A是无限集, 故A⊄{a},AdG={a}≠φ, 于是A是G-可数紧的．

下面讨论G-可数紧子集,G-序列可数紧子集,G-序列紧子集之间的关系．

定理3设G是集X上的方法．若F是X的G-序列紧子集, 则F是X的G-可数紧子集．

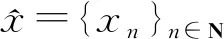
例3G-可数紧子集不一定是G-序列紧子集．

令X=R, 赋予通常拓扑．

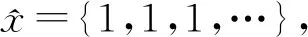
若X是可数紧的序列空间, 则X是序列紧空间[10]．那么, 在序列空间或者G-序列空间下, 是否有相应关系呢?

定理4设G是序列空间X上的正则的子序列方法,则X上每一G-可数紧子集是G-序列紧子集．

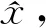
上述定理中的正则方法可以弱化成点式方法．

定理5设G是G-序列空间X上的点式的子序列方法, 则X上每一G-可数紧子集是G-序列紧子集．

证明 设F是X中的G-可数紧子集．由G-是子序列方法和定理2知F是X的可数紧子集．任取F中序列 {xn}n∈N, 下证 {xn}n∈N有G-收敛的子序列．若序列 {xn}n∈N有无限项相同, 因G是点式方法, 结论成立; 若序列 {xn}n∈N满足∀n≠m,xn≠xm, 令A={xn:n∈N}, 因F是可数紧子集, 故A至少有一个聚点x．令B=A{x}, 则B不是闭集．由X是G-序列空间, 知B不是G-闭集,于是存在 {yn}n∈N⊂B⊂A和y∈XB使得 {yn}n∈NG-收敛于y, 此时序列 {xn}n∈N有G-收敛的子序列 {yn}n∈N．由定义6,F是G-序列紧子集．

下面讨论Cakalli[8]定义的G-序列可数紧子集与G-序列紧子集、G-可数紧子集之间的关系．

例4G-序列紧子集不一定是G-序列可数紧子集．

由例3知,F亦是X的G-序列可数紧子集, 故G-序列可数紧子集不一定是G-序列紧子集．

由引理2, 可得:

推论1设G是集X上的方法． 若F是X的G-序列可数紧子集, 则F是X的G-可数紧子集．

结合定理3与例4, 可得G-可数紧子集不一定是G-序列可数紧子集．