锻炼数学思维 提升核心素养
李兆新
(灌云县第一中学,江苏 连云港 222200)
2023年高考数学新课标Ⅰ卷在反套路、反机械刷题上下足了功夫,突出强调对基础知识和基本概念的深入理解和灵活掌握,注重考查学科知识的综合应用能力,落实中国高考评价体系中“四翼”的考查要求.其中,第7题的数列题,就很好地考查了考生的数学探究能力、落实了“四翼”的要求.教师应合理设计、适时引导,引导学生从类比、模仿到自主创新,从而让学生在探究中锻炼数学思维,提升核心素养.
1 真题再现

A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
2 一题多解
思路1 定义法,即{an}为等差数列⟺an+1-an=d.
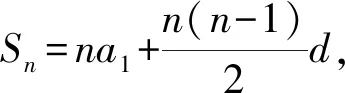

两式相减得an=nan+1-(n-1)an-2nD=n(an+1-an)+an-2nD,即an+1-an=2D,对n=1也成立,因此{an}为等差数列,则甲是乙的必要条件[1].
综上,甲是乙的充要条件,选C.
思路2通项公式法,即{an}为等差数列⟺an=pn+q.
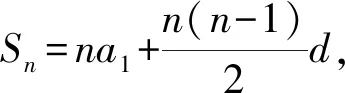

综上,甲是乙的充要条件,选C.
3 题后反思
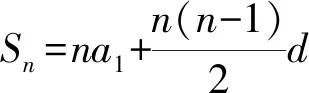
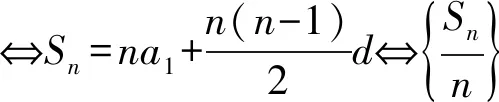
经过探究,可得:
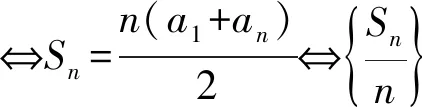

性质3{an}为等比数列(q≠1)⟺Sn=kqn-k(k≠0,q≠1)⟺存在非零常数k,使{Sn+k}为等比数列.
性质4{an}是等比数列(q≠1)⟺Sn=s+tan(s≠0,t≠0,1).
4 课本溯源
2019年人教A版《数学选择性必修第二册》第25页习题7:
已知Sn是等差数列{an}的前n项和.


分析第(1)的结论就说明了甲是乙的充分条件.
5 试题推广
我们先来探究等差数列下角标性质的不等关系.
设{an}是正项等差数列,公差为d(d>0),前n项和为Sn,m,n,p,q均为正整数. 若n 命题1aman 证明先证mn 因为n mn-pq=mn-p(m+n-p)=mn-pm-pn+p2=(m-p)(n-p)<0, 即mn 因为m+n=p+q,mn 命题2mam+nan>pap+qaq. 证明因为m+n=p+q,且d>0,所以 mam+nan-pap-qaq=m[a1+(m-1)d]+n[a1+(n-1)d]-p[a1+(p-1)d]-q[a1+(q-1)d]=(m+n-p-q)a1+[m(m-1)+n(n-1)-p(p-1)-q(q-1)]d=(m2-m+n2-n-p2+p-q2+q)d=[(m2-p2)-(m-p)-(q2-n2)+(q-n)]d=[(m-p)(m+p-1)-(q-n)(q+n-1)]d=λ(m+n+p+q-2)d. 其中λ=m-p=q-n>0,又d>0,且m+n+p+q-2>0,故mam+nan>pap+qaq. 命题3Sm+Sn>Sp+Sq. 命题4SmSn 类比到等比数列,可得到如下的变式题. 变式题已知数列{an}的各项均为正数,记Sn为{an}的前n项和,从下面①②③中选取两个作为条件,证明另外一个成立. ①数列{an}是等比数列;②数列{Sn+a1}是等比数列;③a2=2a1. 注:若选择不同的组合分别解答,则按第一个解答计分. 解答过程留给读者完成. 预测题 设甲:{an+1}是等比数列;乙:{Sn+n}是等比数列,已知两个数列的公比都不等于1,则( ). A.甲是乙的充分条件但不是必要条件 B.甲是乙的必要条件但不是充分条件 C.甲是乙的充要条件 D.甲既不是乙的充分条件也不是乙的必要条件 若{Sn+n}是等比数列,则Sn+n=(a1+1)qn-1,从而Sn-1+(n-1)=(a1+1)qn-2,两式相减得an+1=(a1+1)(1-q)qn-2(n≥2),这对n=1不成立,因此{an+1}不是等比数列,则甲不是乙的必要条件. 综上,甲既不是乙的充分条件也不是乙的必要条件,选D. 对于一道经典的高考题来说,我们不能就题论题,更不能把题目做完了就算了.我们应该从以下的几个角度来进行探究:(1)学生是怎么来解这道题的?(2)试题还可以做哪些推广?(3)试题的题根源自哪里?(4)试题还可以怎么变式?(5)接下来该如何备考?(6)如何进行试题预测?教师可以从以上角度来进行教学设计或者讲评设计,让学生在探究中成长,在探究中锻炼数学思维,提升核心素养.通过研究性学习,积累发现和提出问题、分析和解决问题的经验,养成独立思考与合作交流的习惯,达到做一道题而会一类题的效果[2].
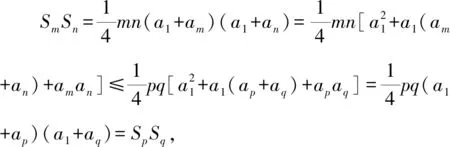
6 变式提升

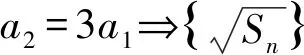


7 高考预测