一道高考解析几何题的多解与课本溯源
杨小瑛
(江苏省江安高级中学,江苏 南通 226500)
解析几何试题是高考的一个难点,它因运算量和思维强度大,令很多考生望而生畏.笔者对高考中的解析几何试题进行探究,获得一些心得.下文以2019年全国Ⅱ卷理科解析几何试题为例,从各种角度给出试题的解析,并对试题进行课本溯源,希望对读者有所启示.
1 真题呈现
2019年高考数学全国Ⅱ卷理科解析几何试题如下:


图1 真题图
(1)求C的方程,并说明C是什么曲线;
(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交C于点G.
(ⅰ)证明:△PQG是直角三角形;
(ⅱ)求△PQG面积的最大值[1].
2 一题多解

(2)(ⅰ)如图1所示,问题等价于证明PQ⊥PG,下文从三个视角来证明.
视角1 常规思路,求出P,Q,G的坐标.
解法1设PQ的斜率为k,则PQ:y=kx(k>0).





故PQ⊥PG,即△PQG是直角三角形[2].
点评该解法虽然有点复杂,但却是最基本的方法,而且为(ⅱ)求△PQG的面积作了铺垫.
视角2椭圆的第三定义.
解法2先证明引理1


点评该解法正是揭示了问题的背景:椭圆的第三定义.
视角3变换的视角,让椭圆“圆”形毕露.
解法3设P(x1,y1),G(x0,y0),则Q(-x1,-y1),E(x1,0),所以kPQ=2kGQ.

⟺2kGQ·kGP=-1
⟺kPQ·kGP=-1.
所以PQ⊥PG,即△PQG是直角三角形.
点评通过伸缩变换,把椭圆变为圆,根据圆周角定理和射影不变量来推导,恰恰揭示了问题的本质.



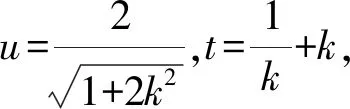



由引理2得,


3 课本溯源
第(1)问的背景是椭圆的第三定义,即引理1:

然而,这个结论(第三定义)却是出自课本:2019年人教A版《数学选择性必修第一册》108页例3.
4 教学思考
4.1 回归课本
高考题虽千变万化,但万变不离其宗.课本是高考试题命制的依据,课本就是根本.我们不仅要熟悉课本的知识体系,更要熟悉课本的例题和习题,而且要对课本的例题和习题进行进一步的探究和推广,打通课本与高考的通道.
4.2 研究高考真题.
通过研究往年的高考真题,不仅可以熟悉高考所考查的题型、考点和解题的思想方法,而且可以探究高考试题的特点,感知高考命题的趋势与动向.高考试题也具有一定的周期性,所以我们有必要对往年的高考真题进行变式探究和深入研究.
4.3 数学思想方法的渗透
圆的很多性质(比如圆周角定理、垂径定理等)都可以类比到椭圆,从而得到一些新的性质. 高考命题人往往也是从这个角度来命制试题,所以在平时的教学中,教师有必要进行拓展,把圆的性质类比到椭圆来研究.又比如,也可以把平面几何的一些性质类比到空间几何,这需要教师在日常的教学中进行渗透.
4.4 数学运算核心素养的培养
很多学生对解析几何综合题“望而却步”,原因是其运算量太复杂.要提高学生的运算能力,需要教师在日常教学中做到以下三点:一是总结一些可以简化运算的思想方法,如设线优化、点差法、换元法、对偶法等;二是要给学生充足的时间,让学生亲自动手作运算;三是教师要当面指点学生,指出其运算出错的地方或者处理不当之处. 如此,学生的运算能力才会越来越好,最终达到培养学生数学运算核心素养的目标.

