结合LSTM 和Self-Attention 的滚动轴承剩余使用寿命预测方法
黄 宇,冯 坤,高俊峰,李周正,江志农,高金吉
(1.北京化工大学信息科学与技术学院,北京 100029;2.北京化工大学高端机械装备健康监控与自愈化北京市重点实验室,北京 100029;3.中国石油天然气股份有限公司炼油与化工分公司,北京 100007)
引言
滚动轴承是机械设备中最常见且极其重要的关键零部件。在设备运行的过程中由于环境、工况等因素的影响,滚动轴承因易出现点蚀、磨损等现象,而成为工业上最易损坏、可靠性最差的零部件之一。在旋转设备中,约有30%的故障是由滚动轴承引起的[1]。因此,对滚动轴承的运行状态进行监测,预测其剩余使用寿命并确定最佳维修点,可以为决策者建立维修方案提供支撑,具有重要意义。
对滚动轴承的剩余使用寿命预测主要有三种主流的方法:基于模型的方法、数据驱动方法和二者混合的方法[2]。基于模型的方法需要大量的专家知识和先验知识,不仅浪费时间和劳动力,而且不具有通用性。因此,研究数据驱动的剩余使用寿命预测方法,实现轴承精准的RUL 预测,是目前的研究热点。基于数据驱动的轴承RUL 预测主要有三个步骤:①从加速度振动信号中提取具有单调性和趋势性的退化特征,表征滚动轴承的衰退过程;②构建健康度指标模型,利用传统人工智能或深度学习的方法学习退化特征与轴承健康度指标之间的复杂映射关系,得到轴承的退化曲线;③对轴承退化曲线进行拟合预测,计算轴承寿命失效点,最终得到轴承剩余使用寿命。
退化特征提取是轴承RUL 预测的前提条件,目的是从轴承原始加速度振动信号中提取出能反映其退化趋势的特征。目前常见的方法是利用深度学习方法从时域、频域以及时频域中提取原始振动信号的退化特征。杨宇等[3]提出一种改进的深度信念网络,直接以滚动轴承原始振动信号作为网络输入,挖掘出原始振动信号深层本质特征。李少鹏[4]将原始信号通过快速傅里叶变换转换为频域幅值信号,然后利用一维卷积神经网络从频域信号中挖掘深层退化特征。WANG 等[5]提出了通过将原始信号的时频表示作为输入,并利用三维深度卷积神经网络提取退化特征的方法。CAO 等[6]将原始信号边缘谱作为输入,利用时间卷积网络提取高级退化特征表示。
上述基于深度学习的特征提取方法往往需要大量标签对深度学习网络进行监督学习,标签的缺乏严重制约了利用深度学习进行退化特征提取,而传统的统计特征难以反映轴承的整个退化过程,单调性和趋势性不明显[7-9]。
此外,利用退化特征构建健康度指标是轴承RUL 预测至关重要的一步,目的是将退化特征映射为趋势性健康度指标。如果模型输出的健康度指标能够很好地反映轴承的退化趋势,便能准确地预测轴承的剩余使用寿命。轴承的振动数据是一种时间序列数据,而循环神经网络(Recurrent Neural Network,简称RNN)具有强大的时间序列处理能力,因此,RNN 被广泛应用于滚动轴承剩余使用寿命预测。GUO 等[10]利用RNN 将提取的8 个时域特征和6 个频域特征映射为健康度指标,并用双指数函数模型拟合预测,得到了很高的预测精度。韩林洁[11]构建了频域幅值累计特征,并用门控循环单元网络进行轴承剩余使用寿命预测。LI 等[12]利用核主成分分析和指数加权移动平均获得了退化曲线,并利用分层门控循环单元网络进行剩余使用寿命预测。WU 等[13]提出了一种动态差异技术,从原始监测数据中提取特征,利用LSTM 学习监测数据背后真正的物理退化机制,并通过实验说明了LSTM 的性能比标准RNN 和门控循环单元(GRU)更优越。
LSTM 是RNN 的变体,其性能比RNN 更为优越。然而,LSTM 仍然有一些不可忽视的缺点。首先,LSTM 不能进行并行处理,LSTM 必须等待前一个数据处理完成才能处理下一个数据,这不仅降低了模型的灵活度,还导致误差逐级累积[14]。其次,LSTM 在训练过程中存在梯度爆炸、梯度消失以及占用大量内存等问题,而这一系列问题目前没有很好的解决方法。此外,当输入序列超过一定长度后,LSTM 会出现记忆衰退现象,即不能有效记忆很久之前的信息[15]。而自注意力机制(Self-Attention)可以很好地解决上述问题。Self-Attention 能让模型对关键信息重点关注并充分学习吸收,能学习任意长度的时间序列信息;且Self-Attention 是并行计算方式,处理速度较LSTM 大大加快[16]。
综上,提出一种利用包络谱特征并结合LSTM和Self-Attention 构建趋势性健康度指标来实现轴承RUL 预测的方法。LSTM 将退化特征编码为高阶特征向量,Self-Attention 对LSTM 隐藏层的输出计算权重系数,并且选择性地保留中间结果,使隐藏层输出向量之间的联系更加紧密,强调关键信息和减少对无效信息的关注,实现了滚动轴承RUL 的准确预测。
1 理论背景
1.1 包络谱特征和皮尔逊相关系数
1.1.1 包络谱特征
包络解调可以有效地将轴承故障信号从高频信号中分离并提取出来[17]。轴承在出现故障时,由轴承故障引起的特征信号被调制到高频带段,此时时域波形和频谱均难以明显体现其故障特征。包络解调方法对信号进行希尔伯特变换和快速傅里叶变换后得到原始信号的包络谱,从包络谱上可以获取到清晰的故障特征。同时,包络解调还可以发现轴承更早期的缺陷,从而提取轴承初期故障特征[18]。
轴承在退化过程中,多数情况下不止存在一种故障即单一故障模式,而是存在多种故障即复合故障模式。因此,各种故障频率会在高频段与多部件的固有频率发生共振。对信号包络解调后,可以在低频段得到故障特征频率。传统的包络解调在得到包络谱后利用低通滤波器滤掉高频段信号,消除高频段信号对故障分析的干扰,但鉴于复合故障模式的复杂性,包络谱的高频段仍可能包含故障特征[19-20]。因此,本文尝试将包络谱按频率均分成n段。这使得在分析低频段故障特征时不会引入高频段信号的干扰,同时还保留了高频段中的故障信息;由于高频段故障特征相对较微弱,按频率分段后再分析高频段信号,减弱了低频段故障信号对机器学习模型特征提取时的绝对主导性,一定程度上放大了高频段信号的故障特征。
1.1.2 皮尔逊相关系数
皮尔逊相关系数用于度量两个向量X和Y之间的相关性,定义如下式所示:
式中Cov表示协方差;D表示方差;ρXY表示向量X和向量Y之间的皮尔逊相关系数,取值范围为[-1,1],|ρXY|越大,说明X和Y的相关性越大。
皮尔逊相关系数消除了不同变量量纲上的差别,即两个变量的位置和尺度变化并不会改变其皮尔逊相关系数,所以通过皮尔逊相关系数理论计算得到的相关性所衡量的是趋势[21]。因此,将包络谱分段后各子频段与标准样本的皮尔逊相关系数作为退化特征,更有利于模型准确表征轴承退化过程的健康度指标。
1.2 长短期记忆网络
LSTM 网络是从标准RNN 改进得来的。LSTM 通过其内部复杂的门运算和引入细胞态,有效缓解标准RNN 的长期依赖问题[22]。遗忘门ft决定上一时刻的细胞态ct-1有多少信息保留到当前时刻的细胞态ct;输入门it决定当前时刻的输入有多少信息存储到当前时刻的细胞态ct中;输出门ot控制当前细胞态ct有多少信息保留到当前时刻输出ht中。图1 为LSTM 单元的内部结构,xt-1,xt和xt+1分别指t-1,t和t+1 时刻的 输入信 息;ht-1,ht和ht+1分别指t-1,t和t+1 时刻的输出信息。
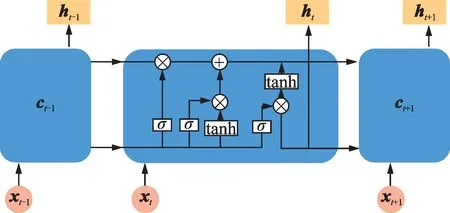
图1 LSTM 结构Fig.1 The structure of LSTM
遗忘 门ft、输入门it、输出门ot、细 胞态ct和输出ht的计算公式分别如下式所示:
式中xt为当前时刻的输入;ht-1为上一时刻的输出;W为权重矩阵;b为偏置;σ(x)=1/(1+ex)为Sigmoid 激活函 数;下 标“f”,“i”,“c”分别表 示矩阵W和偏置b为分别代表遗忘门、输入门、细胞态的参数;⊗表示逐元素相乘法。
1.3 自注意力机制
Self-Attention 是注意力机制的改进,不仅可以快速筛选出关键信息,减少对其他无关信息的关注,还可以降低对外部信息的依赖,更易捕捉输入数据的内部相关性[23]。神经网络通过引入自注意力机制,在解决模型信息过载问题的同时,还提高了网络的准确率和鲁棒性[24]。
Self-Attention 的计算分为两步。步骤1:计算输入序列任意向量之间的注意力权重;步骤2:根据注意力权重计算输入序列的加权平均值。自注意力机制如图2 所示,a(ii=1,2,3,…,t)表示输入序列;v(ii=1,2,3,…,t)表示由输入序列生成的值向量;αti(i=1,2,3,…,t)表示输入序列与各自的向量q和k做运算并经过Softmax 函数后 的结果;b(ii=1,2,3,…,t)则表示输入序列中第i个位置信息与所有位置信息进行注意力机制运算后的结果。
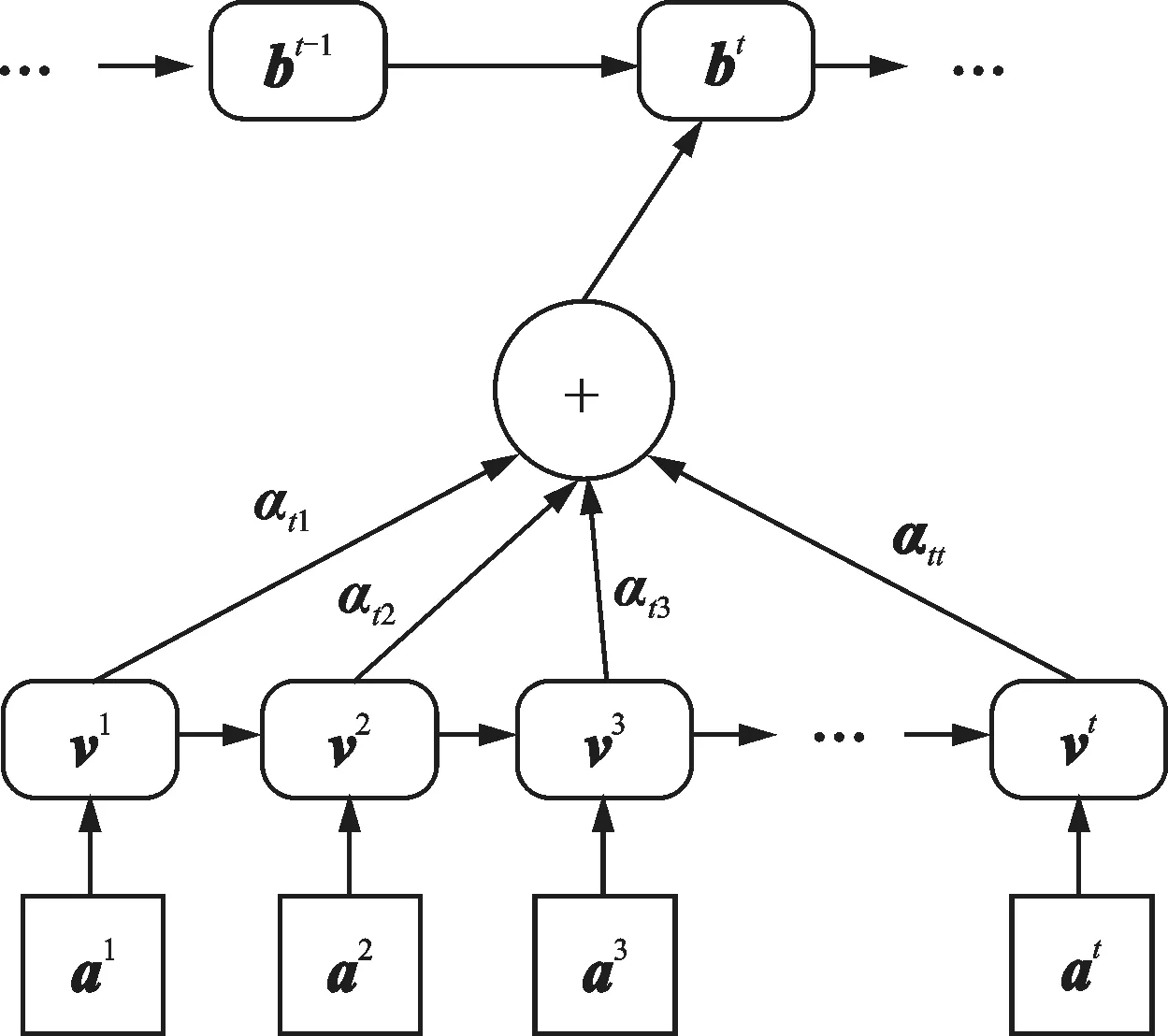
图2 自注意力机制结构Fig.2 The structure of Self-Attention mechanism
Self-Attention 具体运算如下式所示:
式中Q,K和V分别为查询矩阵、键矩阵和值矩阵,由输入X分别与相应的权重矩阵Wq,Wk和Wv相乘得到;dim表示Q,K和V的维数。
2 RUL 预测方法及流程
针对基于深度学习的退化特征提取方法的不足,提出了一种基于包络谱特征和皮尔逊相关系数的退化特征提取方法;并结合 LSTM 和Self-Attention 各自的优点,利用退化特征构建健康度指标,准确表征轴承的退化过程,实现滚动轴承RUL 的预测,流程框图如图3 所示。
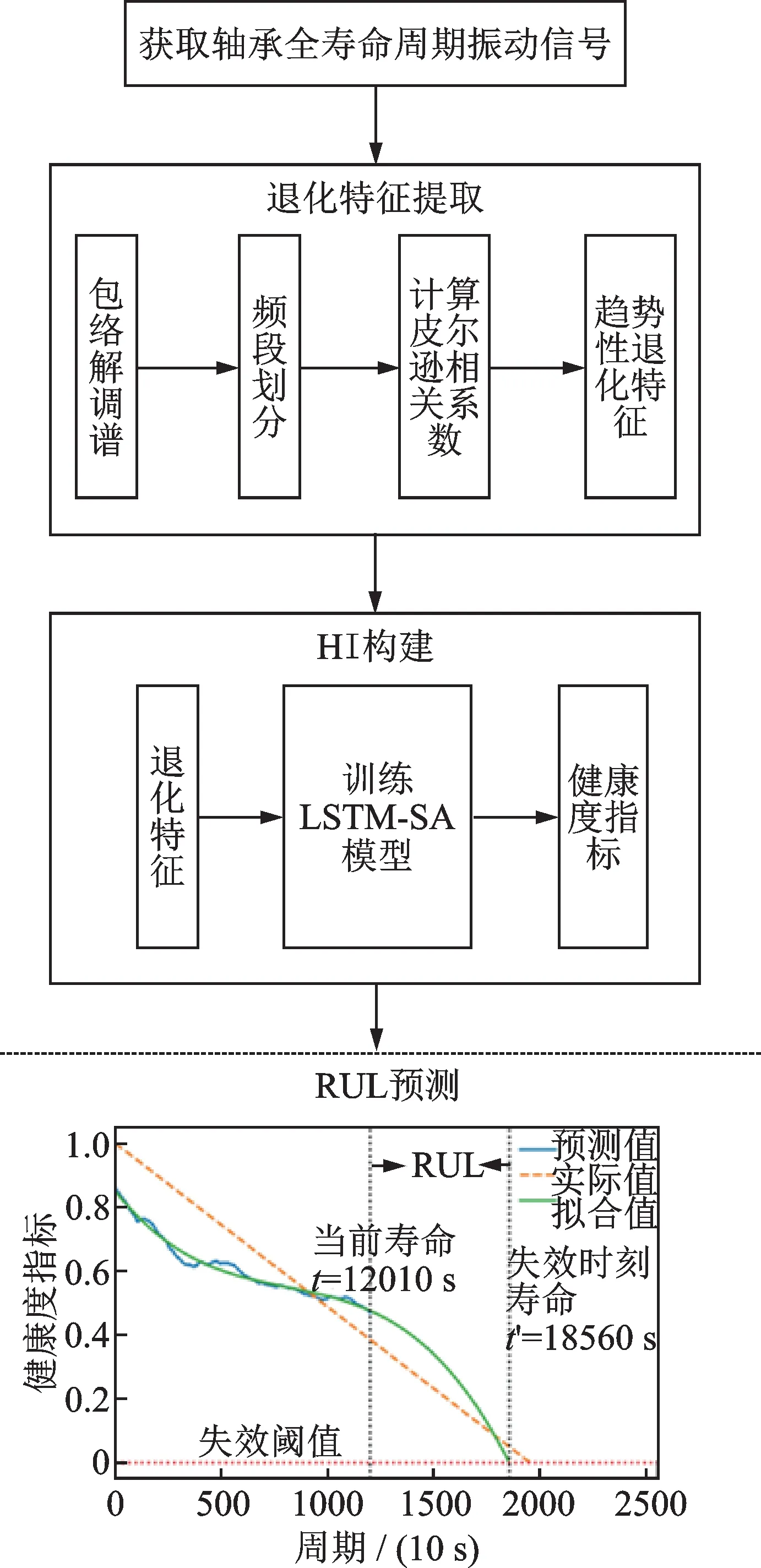
图3 剩余使用寿命预测方法流程图Fig.3 The flowchart of RUL prediction method
具体流程如下:
步骤1:计算信号的包络谱,将包络谱按频率平均划分为n段。以轴承正常运行的振动信号作为标准样本,分别计算各样本每个子频段及标准样本对应频段的皮尔逊相关系数,将计算得到的相关系数作为轴承退化特征。
步骤2:模型的训练数据集是轴承全寿命周期振动信号所提取的退化特征。同时,由于轴承的退化是一个渐变的过程,因此设时刻为t的训练样本的健康度指标HI为:
式中T为轴承的全寿命时间;t为轴承当前运行的时间。将式(11)的计算结果作为训练集的标签,标签的取值范围为0~1。
赋予训练集标签后,利用其训练LSTM-SA 模型。网络随机初始化参数,根据预设的误差函数,计算网络输出与标签之间的相对误差,并朝着误差减小的梯度方向训练参数,直至误差值降到预设的阈值以下或训练次数达到预设的迭代次数为止。训练过程中,将学习率初始化为较小的值,采用Adam 优化器训练网络并自适应调整学习率。
步骤3:利用最小二乘法多项式拟合健康度指标曲线[25],得到轴承的RUL。LSTM-SA 模型的输出是轴承每个时刻的健康度指标,各时刻的健康度指标形成退化曲线。将非全寿命测试轴承信号输入模型,得到非全寿命的健康度退化曲线,拟合该曲线并计算其达到失效阈值的时间点,该时间点就是测试轴承的寿命结束点。轴承的健康度指标取值在0~1 之间,0 表示轴承失效,1 表示轴承完全正常,因此将失效阈值设为0。
3 实验数据验证
3.1 数据描述
为了验证所提方法的有效性,采用IEEE 协会提供的PHM 2012 数据集进行验证[26]。该数据集包含利用加速度传感器采集的17 组轴承的全寿命周期振动信号,其中6 组训练集和11 组测试集,如表1所示。信号的采样频率为25.6 kHz,采样间隔为10 s,单次采样时间为0.1 s。采集设备共采集水平和垂直两个方向的振动信号,根据文献[27-28]的研究,水平方向的振动信号比垂直方向的振动信号提供的有效信息更多。因此,本文采用水平方向的振动信号进行验证。

表1 轴承数据集描述Tab.1 Description of bearing datasets
3.2 滚动轴承RUL 预测
实验首先对数据集进行退化特征提取,第一步需要确定包络谱的分段数n。如前所述,将包络谱分段的退化特征提取方法,可以有效提取轴承早期损伤的故障特征以及优化退化特征的单调性和趋势性,这种性能改进与分段数n有关。因此,接下来将研究n对退化特征的单调性和趋势性的影响。n的初始值分别设置为1,2,3,4,5,6,7 和8,利用主成分分析[29]对不同分段数所提取到的特征降维至一维,计算并比较主成分的单调性和趋势性,选出最优的n。
趋势性和单调性的计算分别如下式所示:
式中xi和yi分别表示时间和特征的值分别表示x和y的平均值。Trend的取值在0~1 之间,值越大,趋势性越强。
式中N表示样本的数量。Mono取值在0~1 之间,值越大,单调性越强。
除此之外,为了从整体上对单调性和趋势性进行度量,定义Cori[30]作为退化特征度量指标,其值越大,说明退化特征越能反映轴承的退化趋势。计算公式如下:
退化特征的Cori对比结果如图4 所示。从图4中可以看出,Cori随着n的增加而增大,并在n=4 时达到最高点。之后,Cori随着n的增加而减小。表2以轴承1_1 和2_2 为例,对比了n取不同值时,退化特征的Cori值。当分段数n太小时,会在退化特征所在频段混入太多干扰信息;相反,当n太大时,会将退化特征所在频段切碎,难以提取出单调性和趋势性明显的退化特征。基于以上分析,在实验中将包络谱分段数n设置为4。
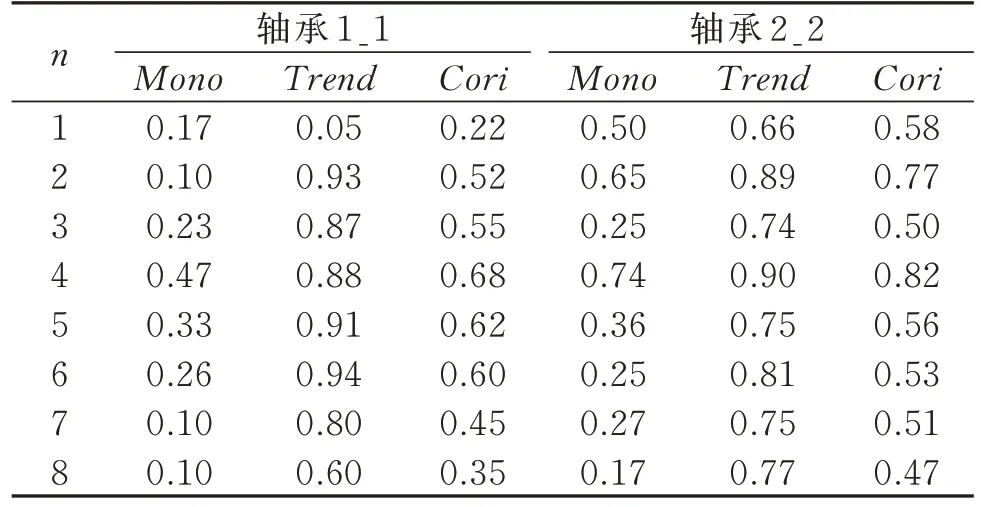
表2 退化特征单调性和趋势性对比结果Tab.2 Comparison results of monotonicity and tendency of degradation characteristics
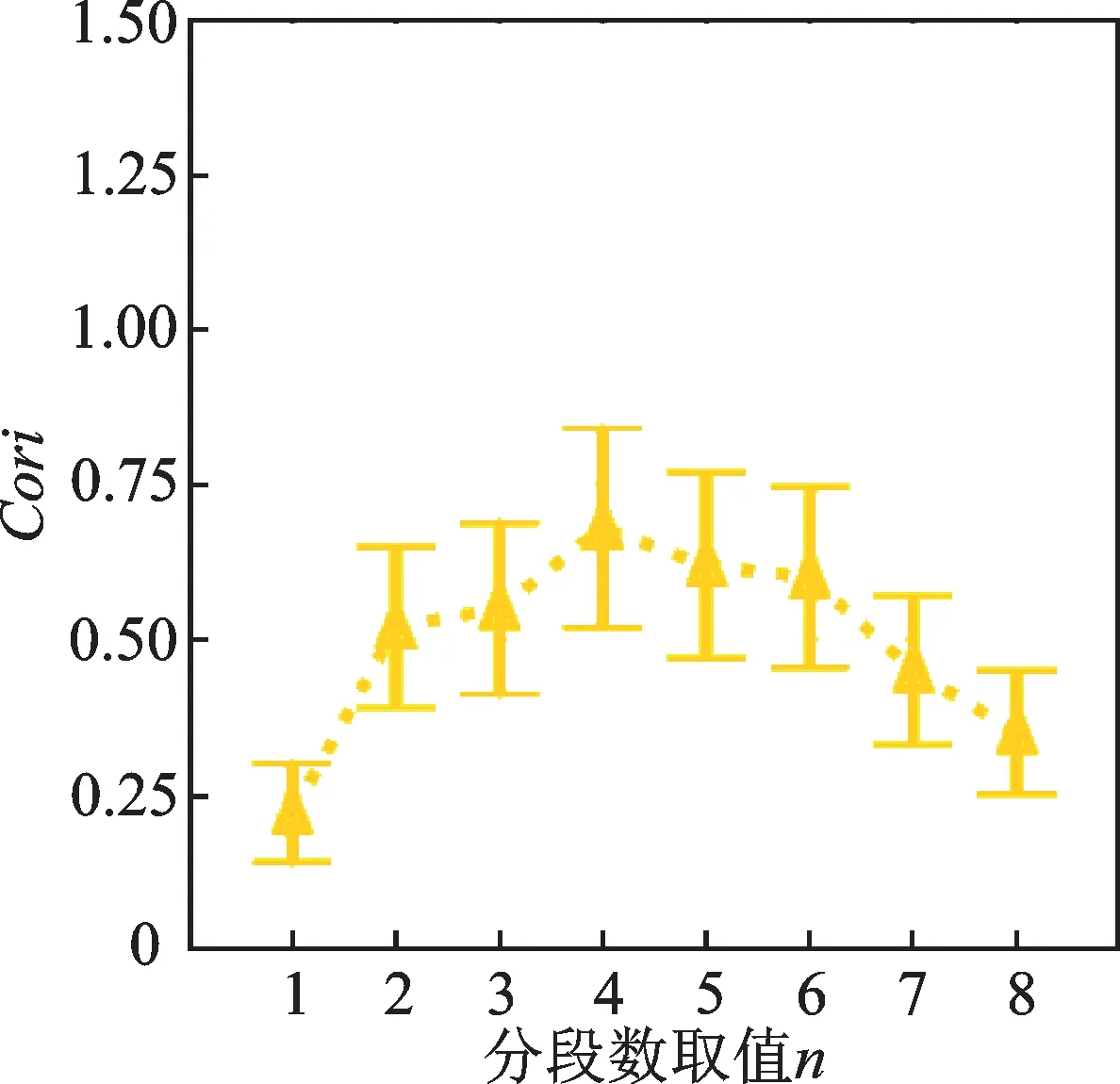
图4 退化特征的Cori 对比Fig.4 Comparison of Cori of degradation features
分段数n确定后,计算原始振动信号包络谱,随后划分子频段并分别计算各频段与标准样本的皮尔逊相关系数,将相关系数作为退化特征。将包络谱划分为n个子频段的方法如下式所示:
式中s1,s2,…,sn分别表示n个子频段的频率范围;F为包络谱的分析频率。将各子频段按式(1)计算皮尔逊相关系数,得到退化特征。
在本实验中,包络谱分析频率为12.8 kHz,如图5 所示。将包络谱按频率划分为4 个子频段,每个子频段的频率范围分别为0~3.2 kHz,3.2~6.4 kHz,6.4~9.6 kHz 和9.6~12.8 kHz,如图6 所示。分别计算每个样本各子频段、全频段及标准样本相应频段的皮尔逊相关系数,计算得到的相关系数作为各样本的退化特征。利用上述退化特征训练LSTM-SA 模型,从而构建健康度指标模型。
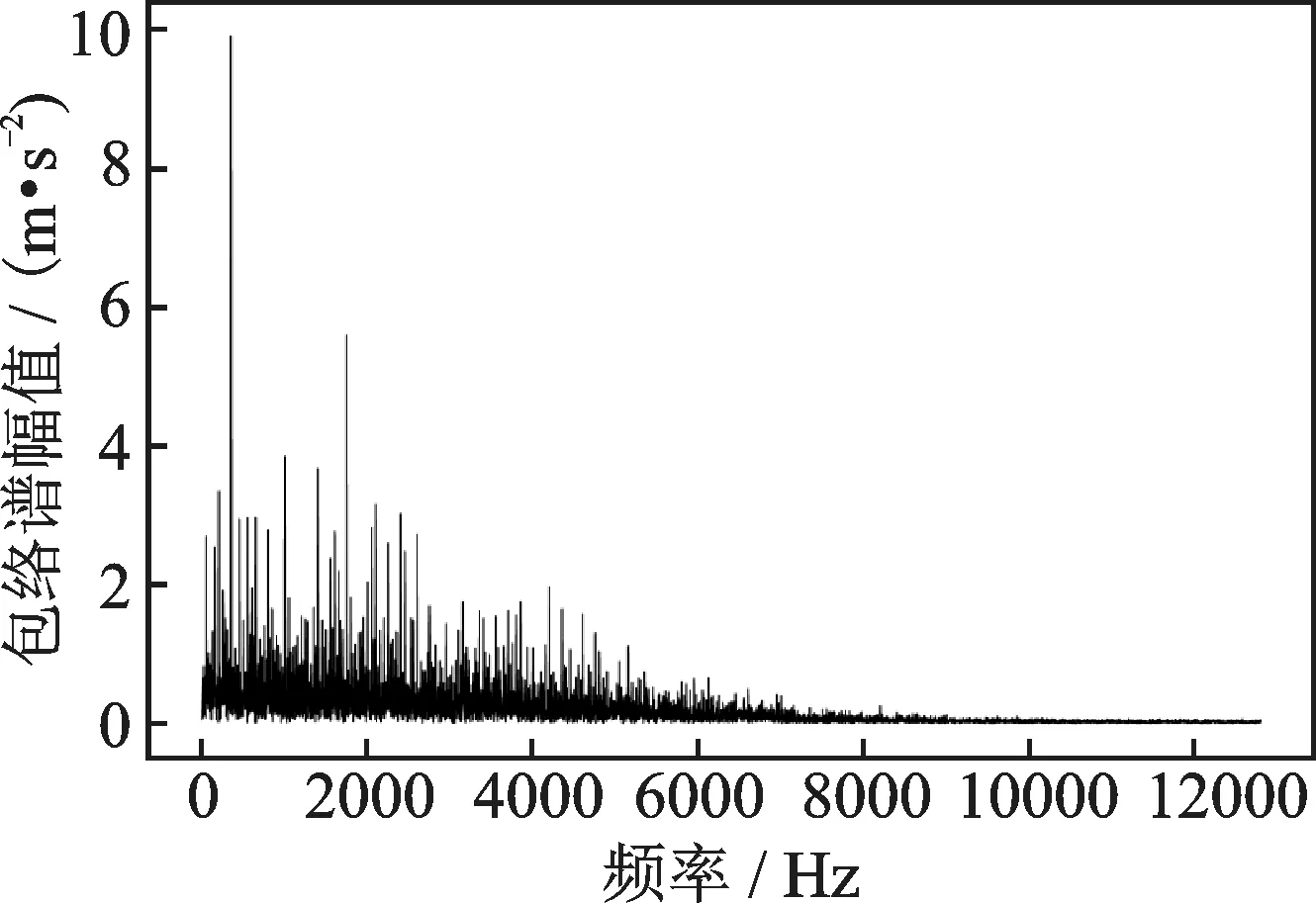
图5 全频段包络谱Fig.5 Envelope spectrum for full band
为了进一步说明退化特征的单调性和趋势性,以训练数据轴承1_1 为例,利用t-SNE 对提取到的退化特征进行可视化分析,如图7 所示。从图7 中可以发现,所提取的特征随着时间有序变化,能够反映出轴承的退化过程。
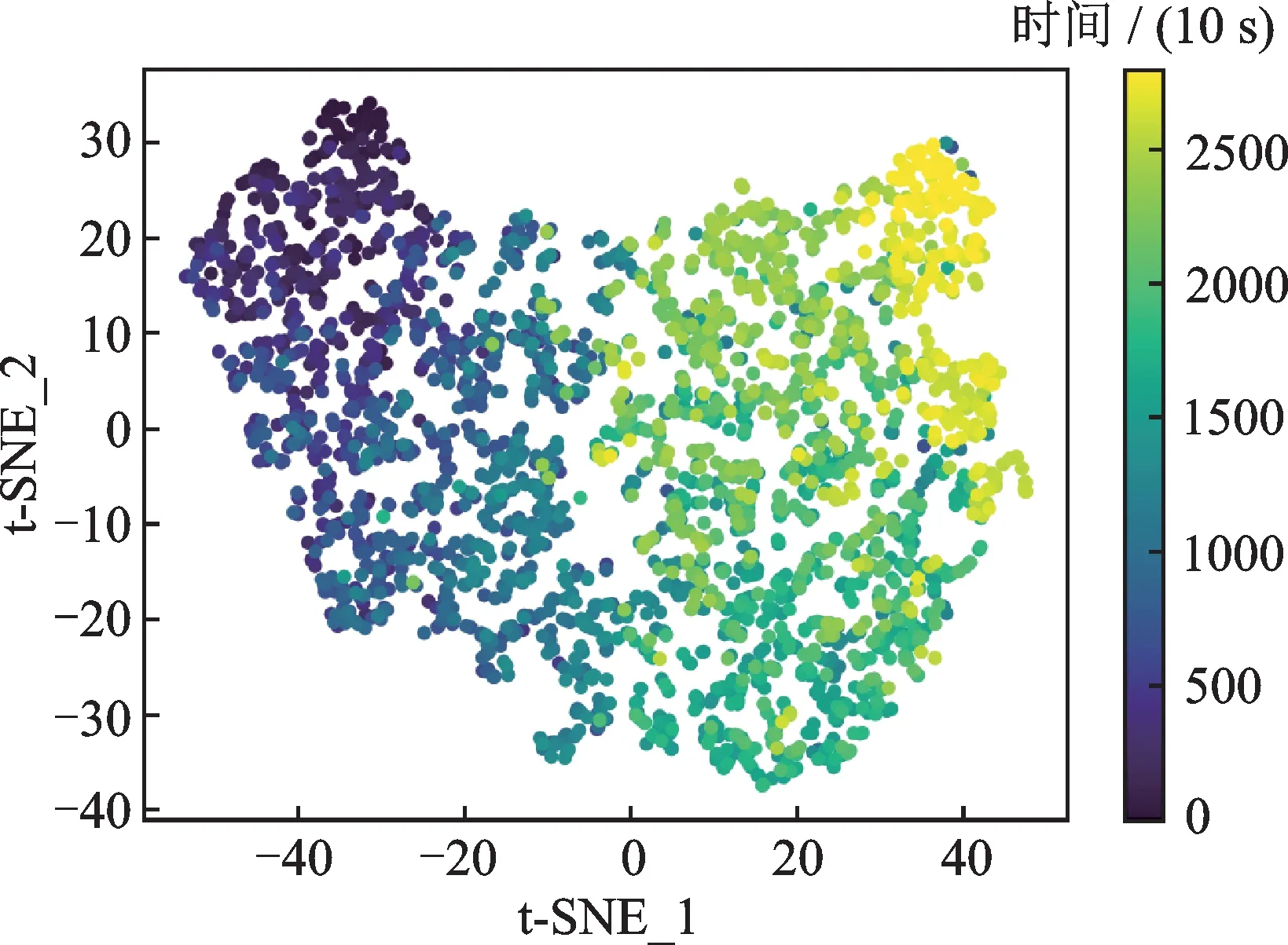
图7 t-SNE 降维可视化退化特征Fig.7 t-SNE reduced dimensional visualization of degradation features
本文按照PHM 2012 数据集的划分,将轴承1_1,1_2,2_1,2_2,3_1 和3_2 全寿命周期数据作为训练集,其余轴承作为测试集。训练集提取退化特征后输入到LSTM-SA 模型进行训练。所提模型由2 层LSTM 层、1 层Self-Attention 运算层和2 层全连接层组成,所有前馈神经网络的神经元个数均为64。初始学习率为0.005,随机初始化权重参数,以均方误差(MSE)作为损失函数,并利用Adam 优化器进行训练。训练和测试的CPU 环境为Intel Core i5,内存为16 GB,深度学习框架为Pytorch 1.10.1。
轴承在运行过程中逐渐发生退化,但其早期运行过程的退化状态表现不明显。以轴承1_7 和2_3为例,分别对两组轴承全寿命时域波形图进行分析,分别求各自的时域特征RMS,如图8 和9 所示。从图8 和9 中可以看出,轴承1_7 和2_3 在运行的前期和中期RMS 变化平稳,直到轴承损坏后期才出现RMS 的跳变。由此可知,轴承早期退化不明显,难以捕捉其退化趋势。
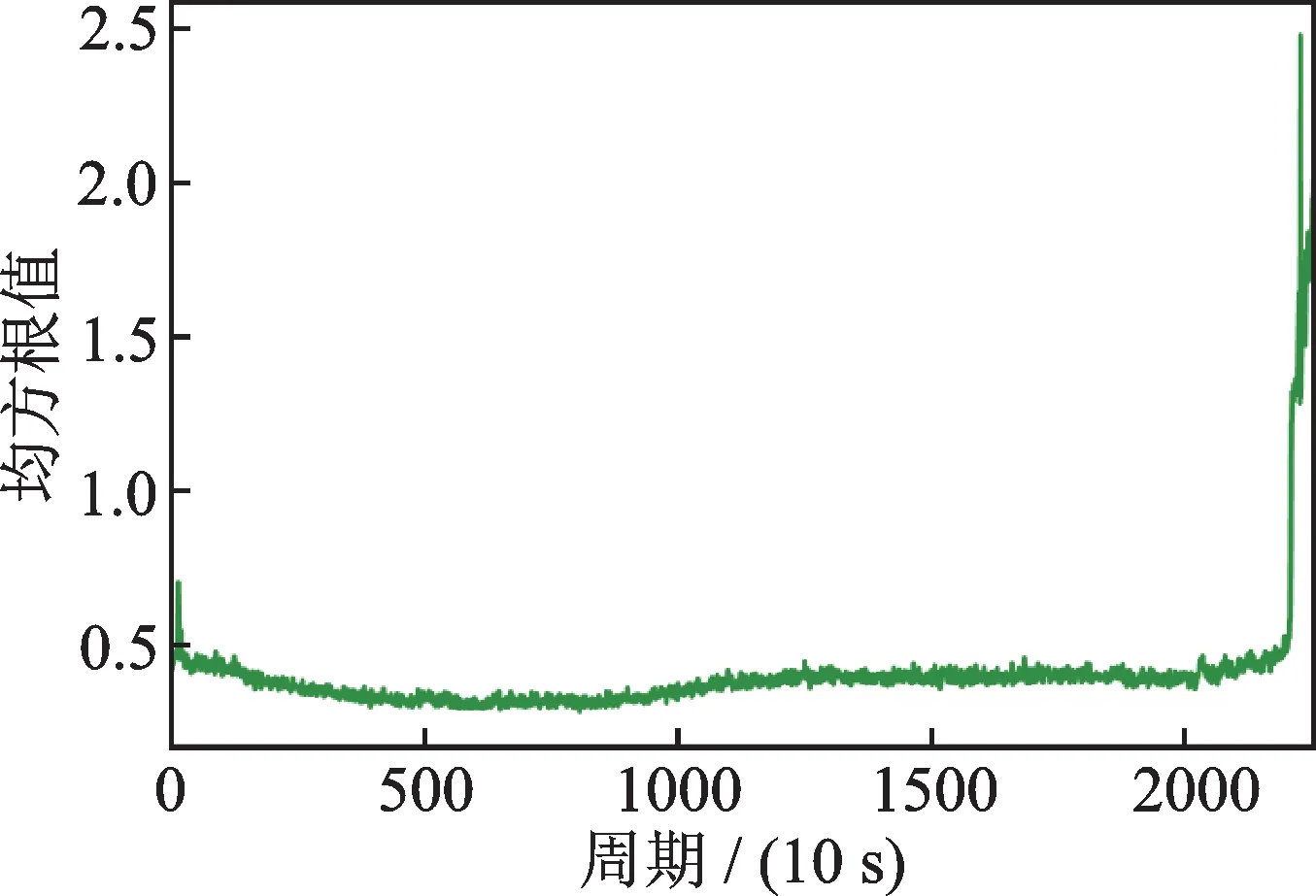
图8 轴承1_7 原始振动信号均方根值Fig.8 RMS value of original vibration signal of bearing 1_7
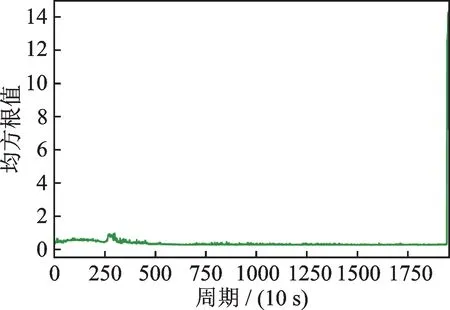
图9 轴承2_3 原始振动信号均方根值Fig.9 RMS value of original vibration signal of bearing 2_3
轴承1_7 和2_3 的健康度指标如图10 和11 所示。从图10 和11 中可知,轴承的健康度指标缓慢变化,较好地反映了轴承在运行过程中的退化状态。由于存在局部振荡,采用Savitzky-Golay 滤波器[31]对健康度指标进行平滑处理,消除局部振荡影响并使健康度指标的退化趋势更为平缓。由图中健康度指标的变化趋势可知,所提方法构建的健康度指标具有明显单调性,能够反映轴承的退化过程,且对轴承早期退化特征敏感。图12 展示了训练集中6 个轴承的健康度指标,针对轴承每个时刻的运行状态,均给出0~1 之间的量化指标。
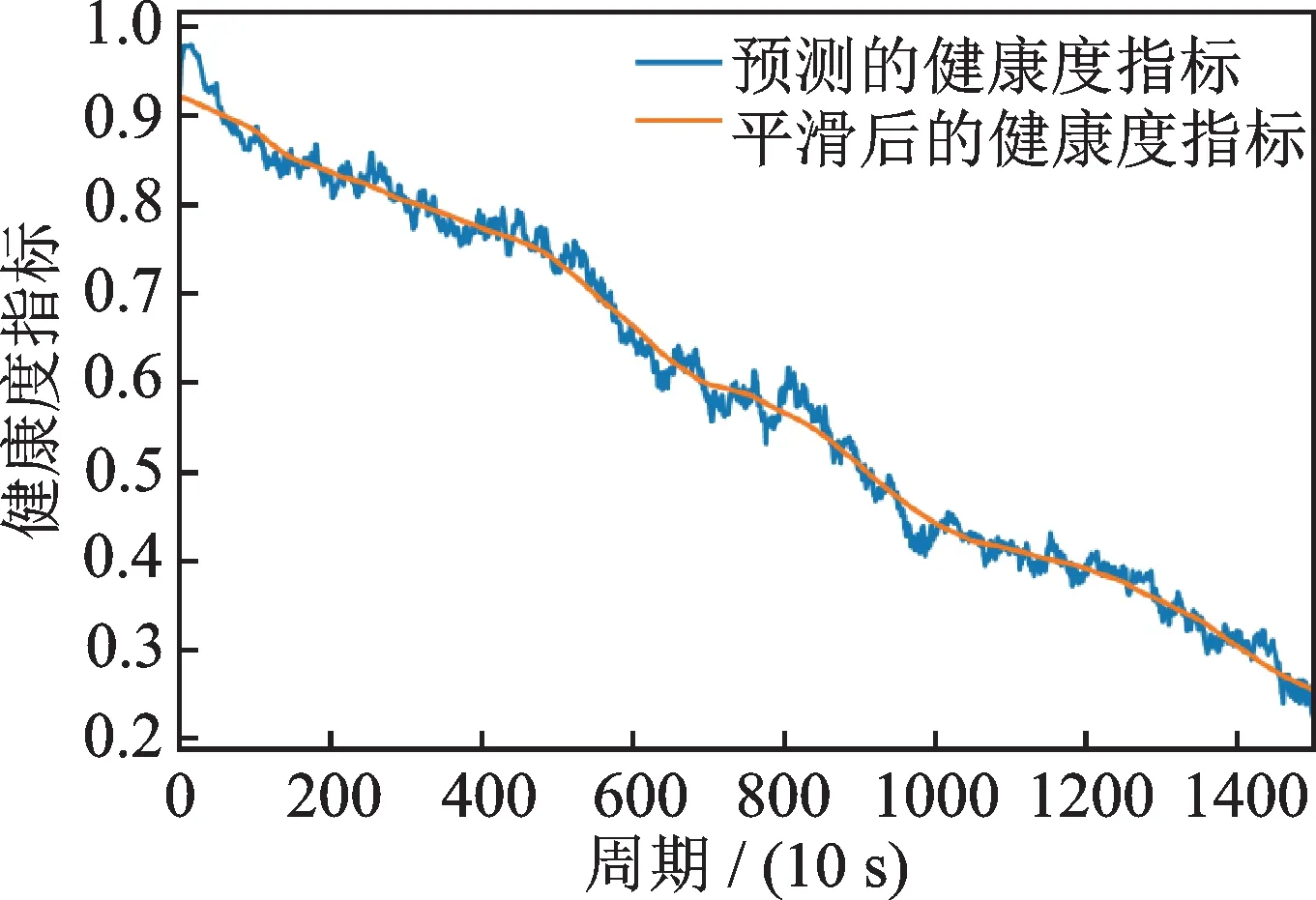
图10 轴承1_7 的健康度指标Fig.10 Health indicator of bearing 1_7
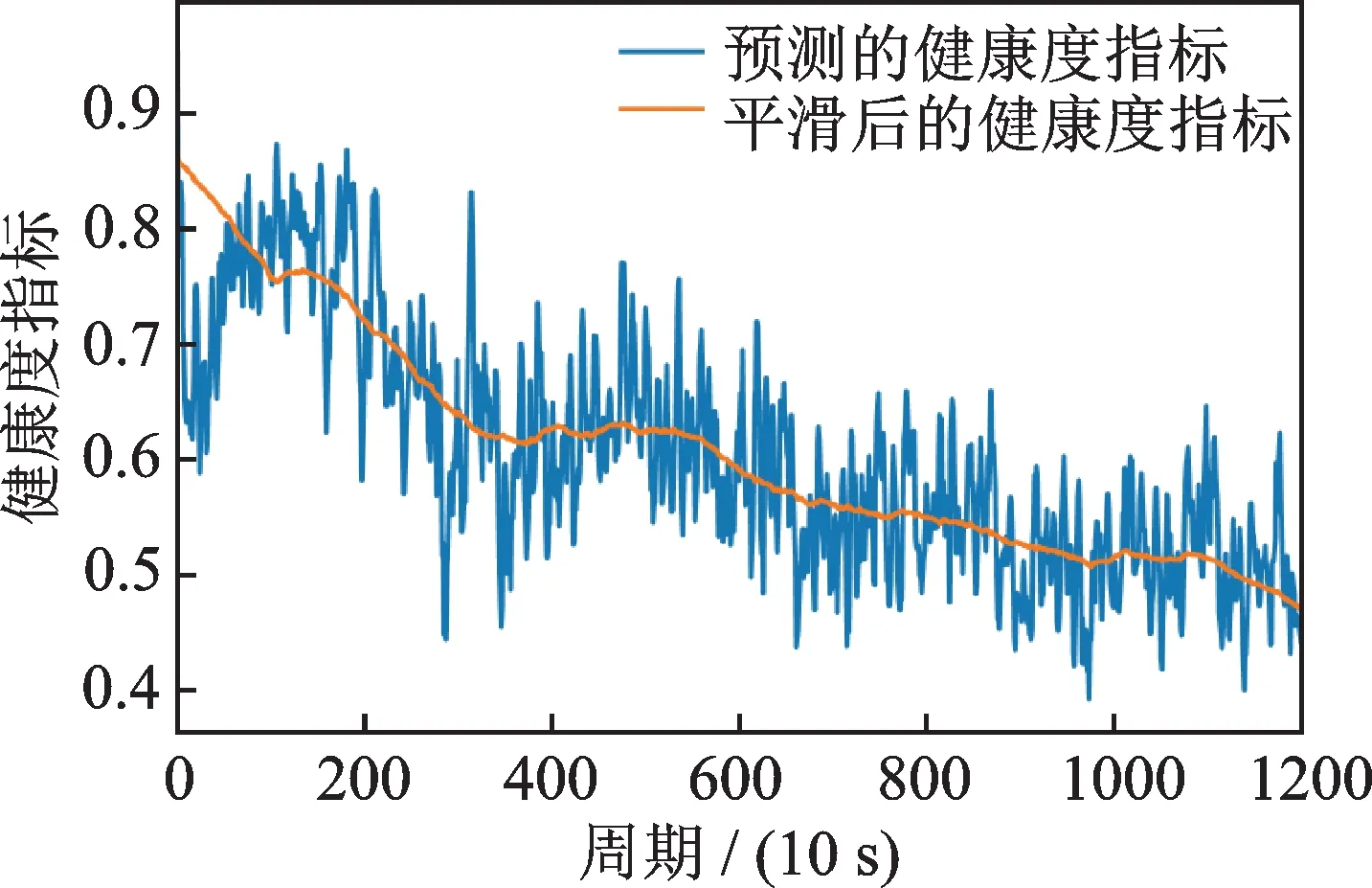
图11 轴承2_3 的健康度指标Fig.11 Health indicator of bearing 2_3
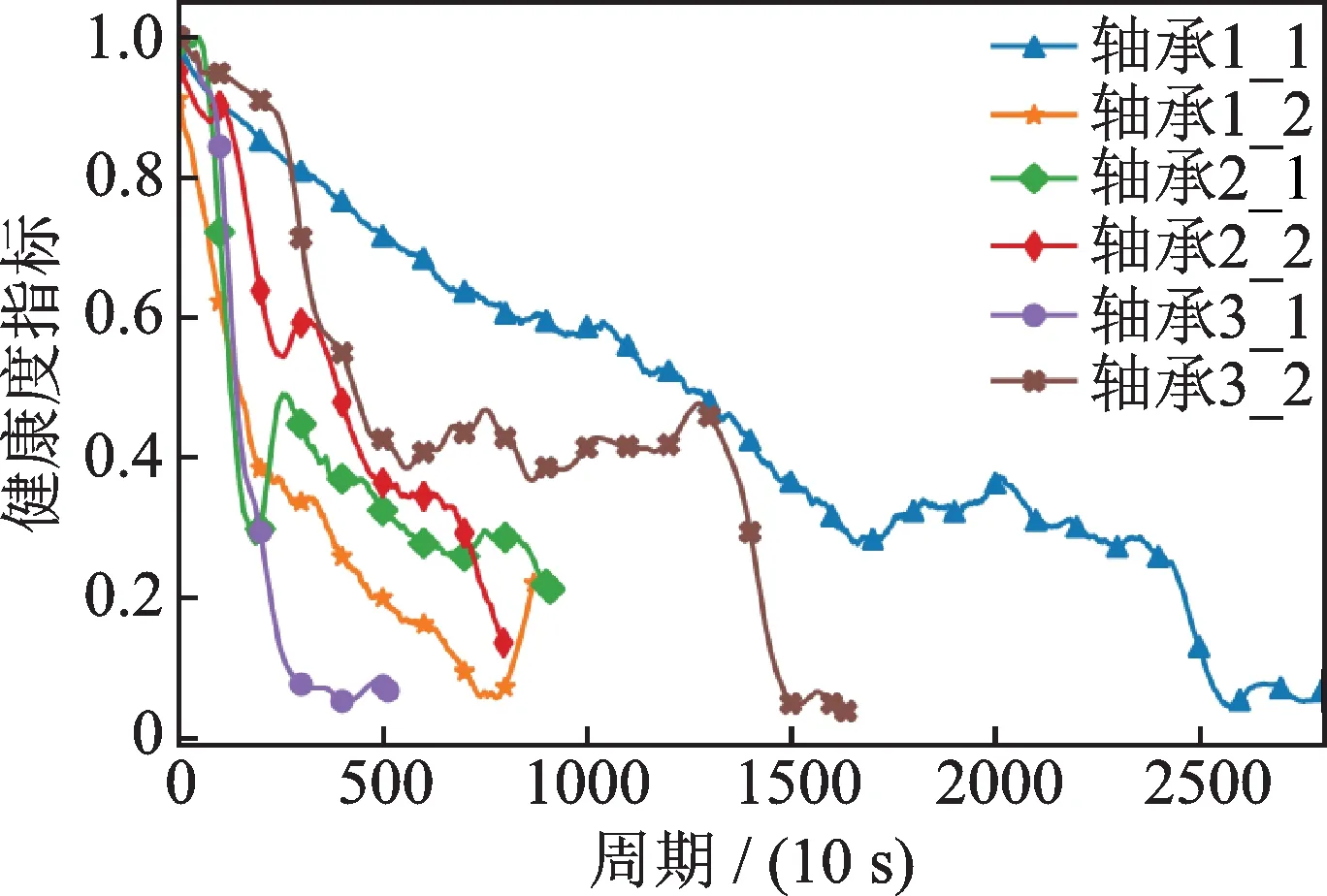
图12 训练集轴承的健康度指标Fig.12 Health indicators of bearings in training set
为验证所提方法构造的健康度指标对提高滚动轴承RUL 预测精度的作用,利用最小二乘法多项式拟合由健康度指标得到的轴承退化曲线,预测轴承的失效点,从而得到轴承的RUL。选取三次多项式进行退化曲线拟合,其公式为:
式中y表示健康度指标;k表示第k个样本,k=1,2,…,N;a,b,c和d表示待拟合的系数。
设t为轴承当前运行时间,当所预测的健康度指标达到失效阈值0 时,求对应失效时间t',二者之差即为预测的剩余使用寿命:
以轴承1_7 和2_3 为例,图13 和14 分别为轴承1_7 和2_3 的剩余使用寿命预测结果。已知数据集中轴承1_7 当前寿命为15020 s,从图13 可知,预测的失效时刻为20160 s,由式(19)计算得到RUL 的预测值为5140 s,而真实剩余使用寿命为7570 s。同理,已知轴承2_3 的当前寿命为12010 s,从图14可知,失效时刻为18560 s,则预测RUL 为 6550 s,而真实剩余使用寿命为7530 s。
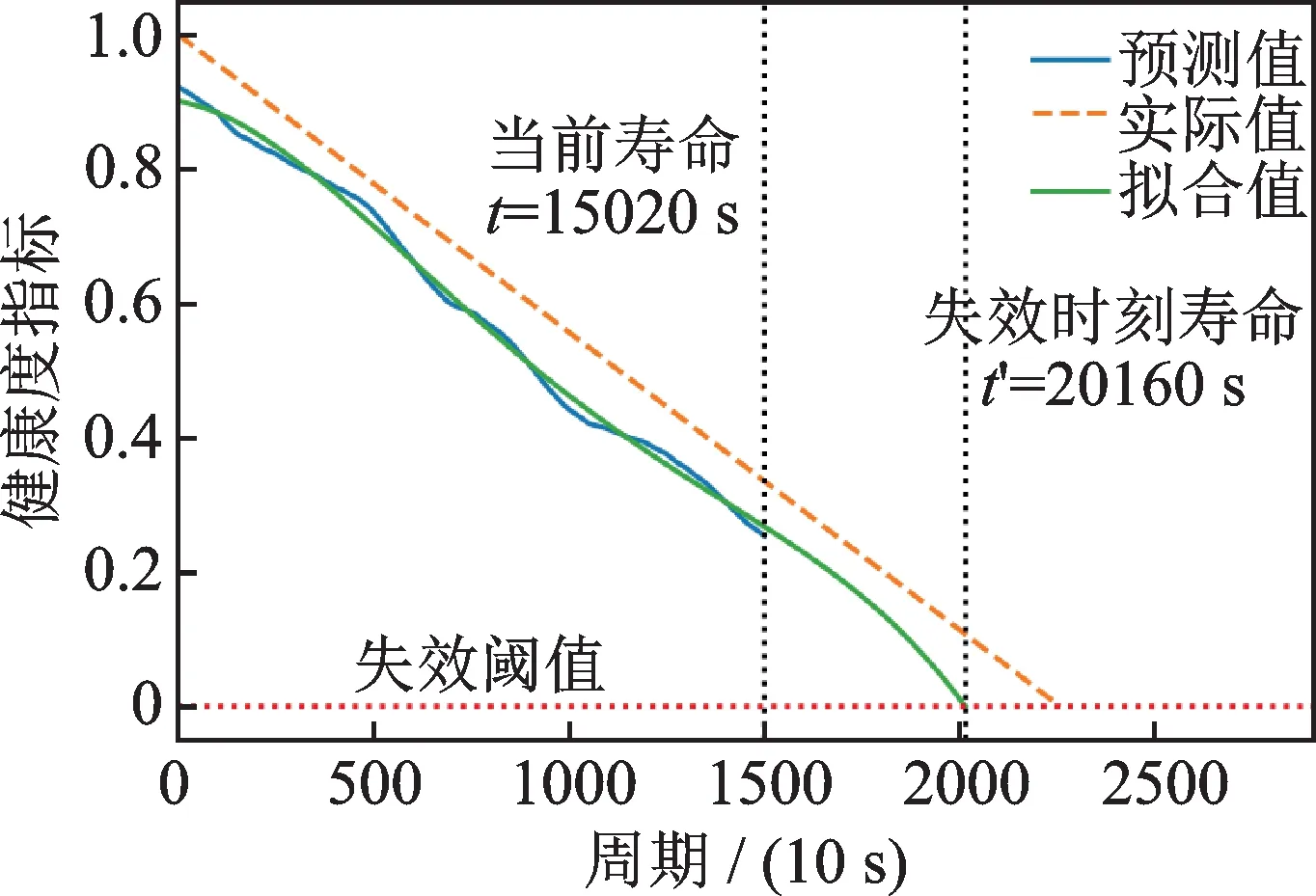
图13 轴承1_7 的RUL 预测结果Fig.13 RUL prediction results of bearing 1_7
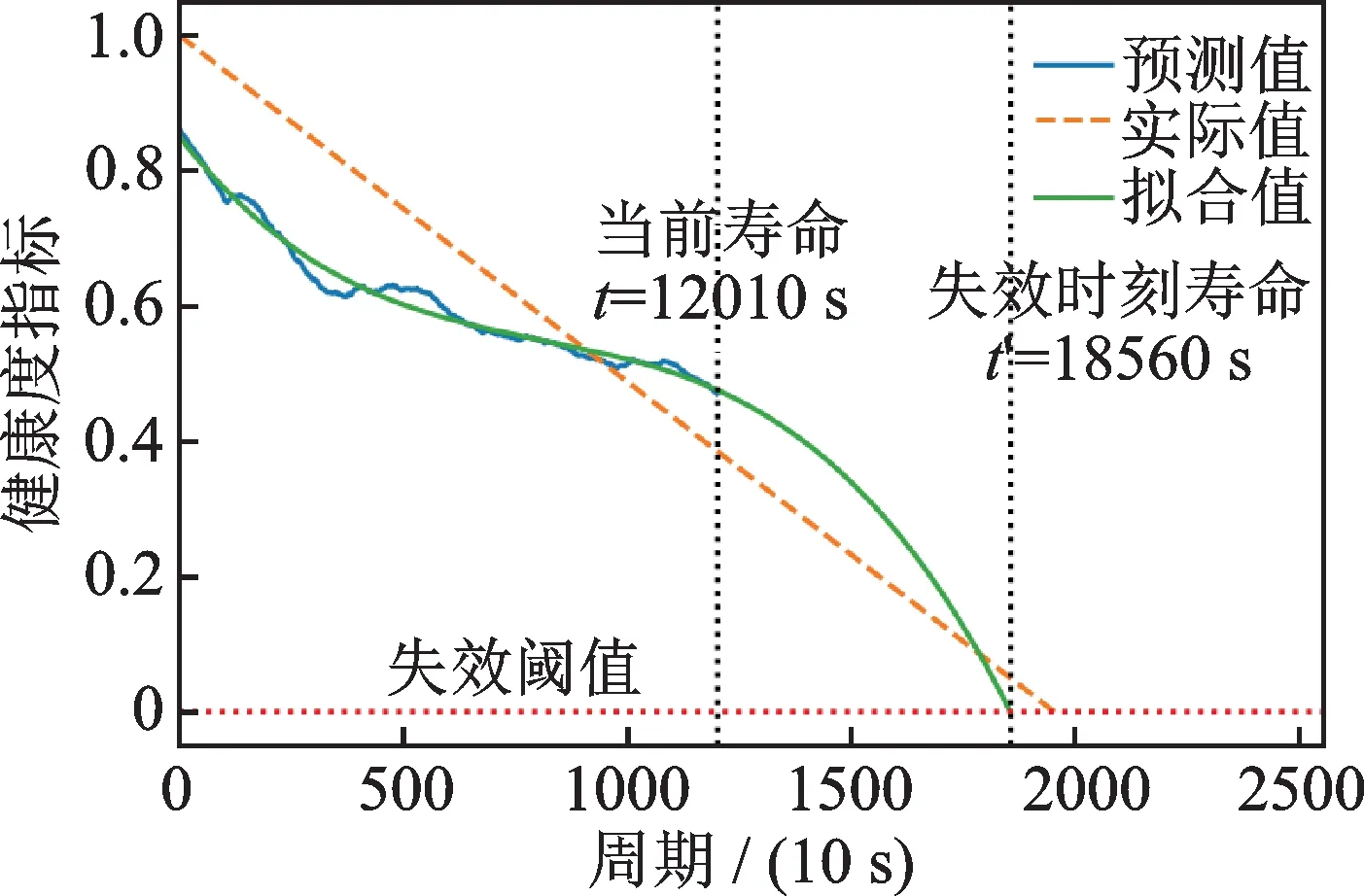
图14 轴承2_3 的RUL 预测结果Fig.14 RUL prediction results of bearing 2_3
3.3 模型评估与误差分析
本文采用误差Ei来评估模型的预测精度,如下式所示:
式中 actRULi表示第i个测试轴承的真实剩余使用寿命;predRULi表示第i个测试轴承的预测剩余使用寿命。
除评估模型的预测精度之外,还需建立一个总体指标来评估模型的有效性,即是否超前预测或滞后预测。因此,本文采用PHM 2012 数据集设立的模型平均得分Score来评估模型的有效性。计算方法如下式所示:
式中Ai表示第i个轴承的得分。
图15 展示了误差Ei与得分Ai之间的关系。从图15 中可以看出,当超前预测,即Ei>0 时,模型的得分更高;反之,当滞后预测,即Ei≤0 时,模型的得分较超前预测低。这是因为在实际生产过程中,超前预测比滞后预测更有意义,因此该得分计算方法对滞后预测进行了惩罚,具有公平性与合理性。
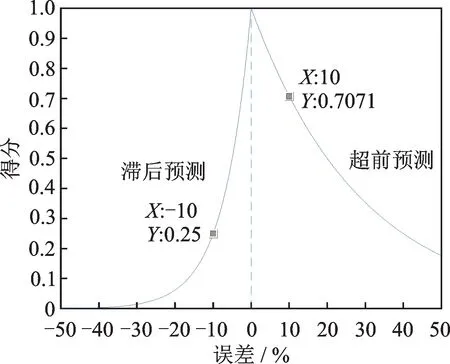
图15 误差Ei 与得分Ai 的函数关系Fig.15 Function relationship of error Ei and score Ai
表3 列出了测试集中11 个轴承的平均绝对预测误差以及模型平均得分,采用Transformer Encoder模 型[7]、SOM模型[32]以 及CNN-LSTM模型[33]进 行对比实验。其中文献[7]和[32]先提取退化特征建立健康度指标,再进行RUL 预测,文献[33]属于“端到端”的RUL 预测方法。从对比结果可以看出,本文提出的方法相较于文献[7],[32]和[33],平均绝对误差分别降低了43.18%,62.57%和59.44%,平均得分分别提高了10.87%,45.71%和34.21%。此外,为了进一步说明利用包络谱分段并计算皮尔逊相关系数提取退化特征的有效性,需要增加对比实验,即不对包络谱分段,对整个包络谱计算皮尔逊相关系数提取退化特征,并进行RUL 预测,对比结果如表4 所示。由表4 可知,包络谱分段比不分段的平均绝对预测误差降低了35.56%,Score提高了49.02%。
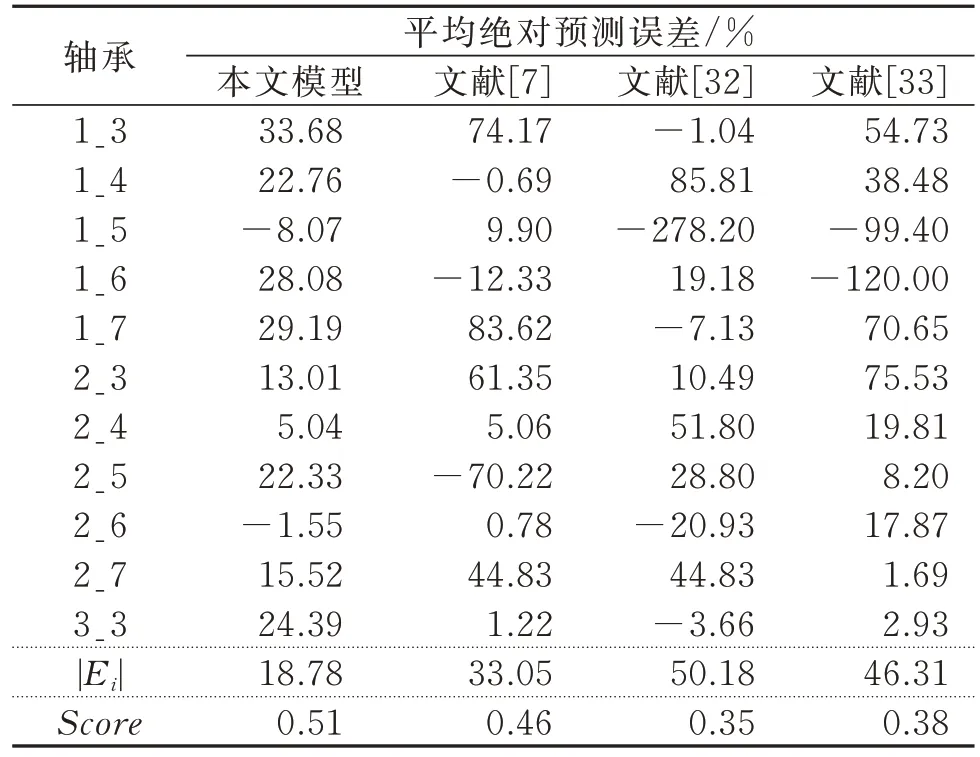
表3 RUL 预测结果与比较Tab.3 RUL prediction results and comparisons

表4 对比实验结果Tab.4 Comparison of experimental results
4 工程实际数据验证
本节将所提方法应用于实际现场设备数据,进一步验证方法的有效性。该数据来源于某石化企业离心泵,该泵为交流异步电机驱动、滚动轴承双支撑结构,额定转速2980 r/min。如图16 所示,泵两端的轴承座(3#轴承和4#轴承)上均安装了IEPE 振动加速度传感器,型号为PCB 608A11,线性频响范围为0.5~10 kHz,量程为±50g。图16 中,Ha 表示水平方向的加速度;Va 表示垂直方向的加速度。每个轴承均采集了垂直和水平方向的振动信号。每个加速度传感器的采样频率均被设定为25.6 kHz,采样间隔为10 s,单次采样时间为0.64 s。在监测的过程,泵两端的轴承发生了退化,最终轴承彻底损坏。图17 为3#轴承振动信号波形图,从图17 中可以看出,信号的幅值在轴承损伤的最后阶段随着时间而增加。
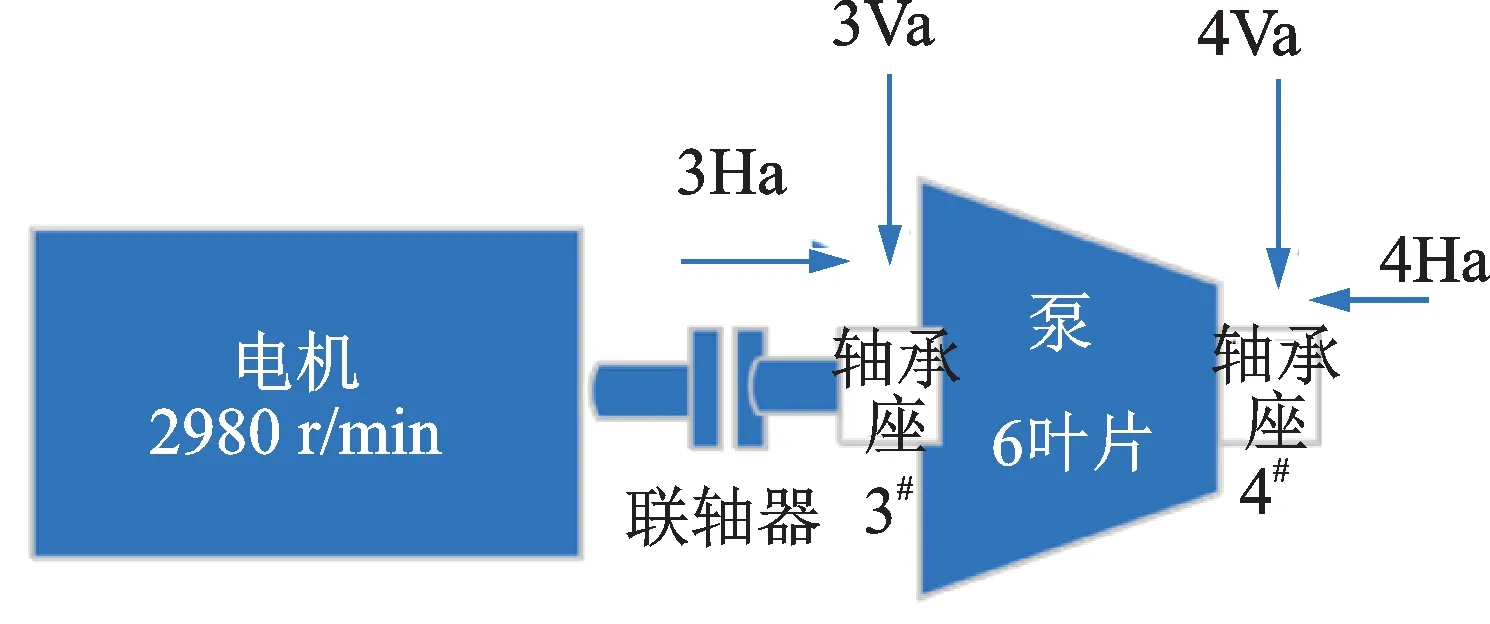
图16 泵的测点布局图Fig.16 Survey point layout diagram of a pump
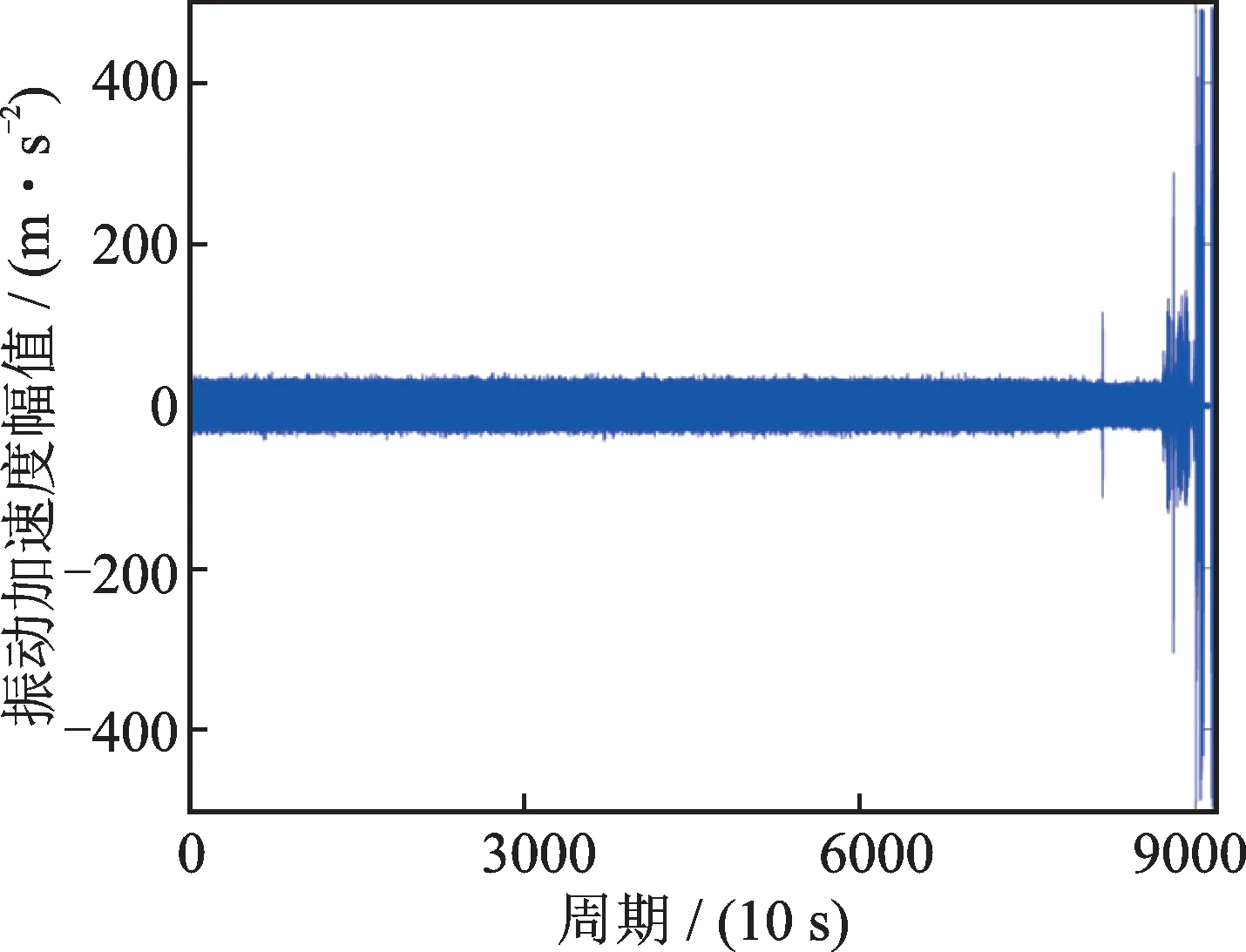
图17 3#轴承时域振动信号Fig.17 Time domain vibration signal of 3# bearing
在现场设备数据的验证过程中,采用了与第3 节相同的操作流程和相同的n值,在相同的实验环境下进行训练和验证。为了突出LSTM-SA 模型的优势,文中用基于标准递归神经网络(Standard-RNN)和基于卷积神经网络(CNN)的RUL 预测模型进行比较。图18为本文提出的基于LSTM-SA 模型的RUL 预测结果;图19 和20 分别为基于Standard-RNN 和CNN的RUL 的预测结果。结合表5 三种模型的比较结果可以看出,LSTM-SA 模型的平均预测误差分别比Standard-RNN 和CNN 模型降低了39.58% 和74.86%。该结果也进一步说明LSTM-SA 模型可以有效地预测滚动轴承的剩余使用寿命。
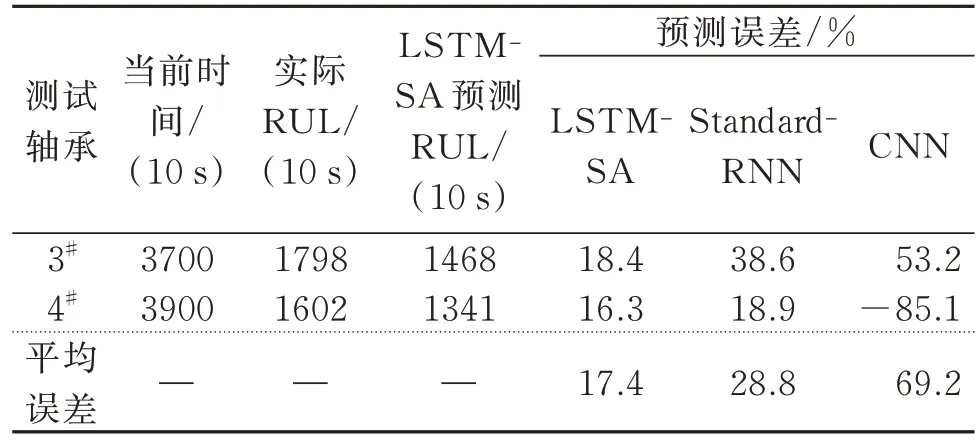
表5 RUL 预测结果与比较Tab.5 RUL prediction results and comparisons
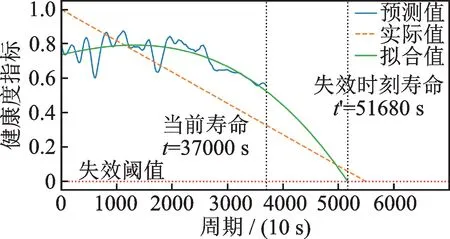
图18 LSTM-SA 模型的RUL 预测结果Fig.18 RUL prediction results of LSTM-SA model

图19 Standard-RNN 模型的RUL 预测结果Fig.19 RUL prediction results of Standard-RNN model
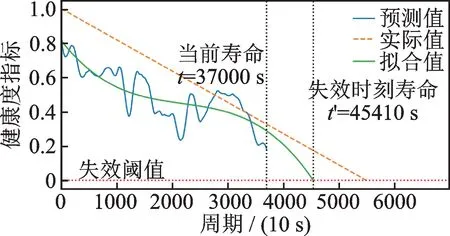
图20 CNN 模型的RUL 预测结果Fig.20 RUL prediction results of CNN model
5 结论
RUL 的预测精度很大程度上依赖于所构建的HI。所提出的方法结合包络谱分段特征和LSTM-SA 模型提高了滚动轴承RUL 的预测准确率。在HI 的构建过程中,提出了基于包络谱特征的退化特征提取方法。将退化特征输入到LSTM-SA中构建HI。为了验证所提出方法的有效性,使用公开的实验数据和真实现场数据进行验证。在实验数据集的验证中,所提出方法比文献[7],[32]和[33]中的方法表现更好。此外,真实现场数据的验证表明,所提出方法比基于Standard-RNN 和基于CNN的方法更能有效地预测泵轴承的RUL。