地铁列车振动对颐和园北宫门古建筑木结构影响的实测与分析
巴振宁,符瞻远,付继赛,马鸣昊,高愈辉
(1.天津大学建筑工程学院,天津 300350;2.天津大学国际工程师学院,天津 300072)
引言
木结构是中国古代建筑重要的结构形式,广泛分布于中国各地,具有极高的艺术价值、历史意义和科学价值,但由于年代久远且结构形式复杂,具有易损伤、修复难度大等特点[1]。
近年来随着轨道交通建设的快速发展,越来越多的地铁线路建设在木结构古建筑附近,地铁运行产生的长期、反复的振动荷载,必然会对其安全造成不可忽视的影响。许多学者如马蒙等[2-3]、李团社等[4]、巴振宁等[5]系统地研究了古建筑木结构在地铁线路运行下的振动响应,对中国制定针对木结构古建筑的保护措施,减小地铁运行对临近木结构古建筑带来的危害具有指导意义。
目前,国内外学者通常采用经验法[6-7]、数值法[8-9]和现场测试法[10-11]对地铁运行振动对古建筑的影响进行研究。然而,经验法无法全面考虑影响轨道交通振动的诸多因素[12];数值法具有较强的便捷性,可用于多种工况分析,但数值模型的假设对计算结果的精度有较大影响[13];现场测试法结果最为准确,但仅适用于针对现有线路进行分析[14]。
鉴于中国对古建筑的保护愈发重视,开展相关古建筑振动测试较为困难,难以获得相关的实测动力参数。此外,关于地铁列车振动对木结构古建筑影响的参数化分析虽有一定研究,但较少考虑线路与古建筑之间夹角等情况。
本文以颐和园北宫门和北京市地铁4 号线为研究对象,采用大型有限元分析软件ABAQUS,建立了列车-隧道-土层-木结构古建筑耦合模型。参照《古建筑防工业振动技术规范》GB/T 50452—2008[15]建议的评估方法,以速度半峰峰值为限值,将现场实测结果与有限元计算结果进行对比,验证了模型的精度,在此基础上,进一步研究了地铁线路与古建筑之间的夹角和距离、列车速度以及隧道埋深对木结构古建筑的影响。
1 工程概况
北宫门位于北京市海淀区颐和园内,曾因战乱损毁,重建于清代同治年间(19 世纪70 年代),距今约150 年的历 史[16]。建筑高度为12 m,通面宽23.89 m,通进深5.14 m。其结构形式为二层木结构建筑。结构整体从上到下分为屋架层和柱网层,一层与二层柱网结构相同,屋架与梁采用斗拱形式连接,梁柱采用榫卯形式进行连接,北宫门建筑整体结构如图1~4 所示。

图1 北宫门正立面图Fig.1 The front elevation of the North Palace Gate

图2 北宫门侧立面图Fig.2 Side elevation of the North Palace Gate
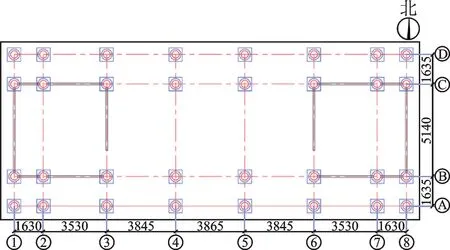
图3 北宫门一层柱网分布图(单位:mm)Fig.3 Distribution map of column network on the first floor of the North Palace Gate(Unit:mm)
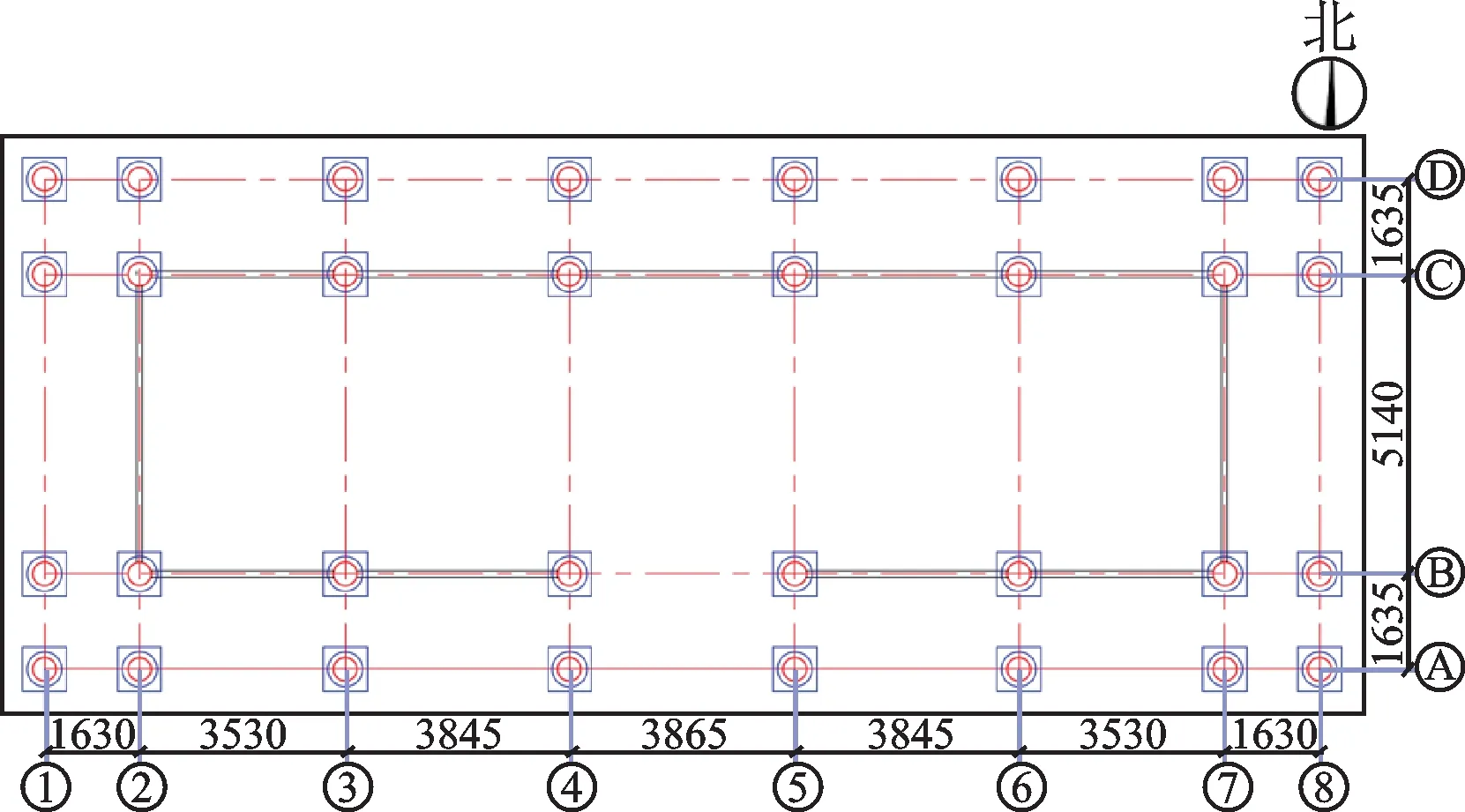
图4 北宫门二层柱网分布图(单位:mm)Fig.4 Distribution map of the column network on the second floor of the North Palace Gate(Unit:mm)
北京地铁4 号大兴线在北宫门的东北部穿过,结构中心位置距地铁线路约为100 m,地铁线路的走向与建筑长轴夹角为45°,地铁隧道埋深为10 m,地铁运营车速为60 km/h,场地平面布置如图5所示。
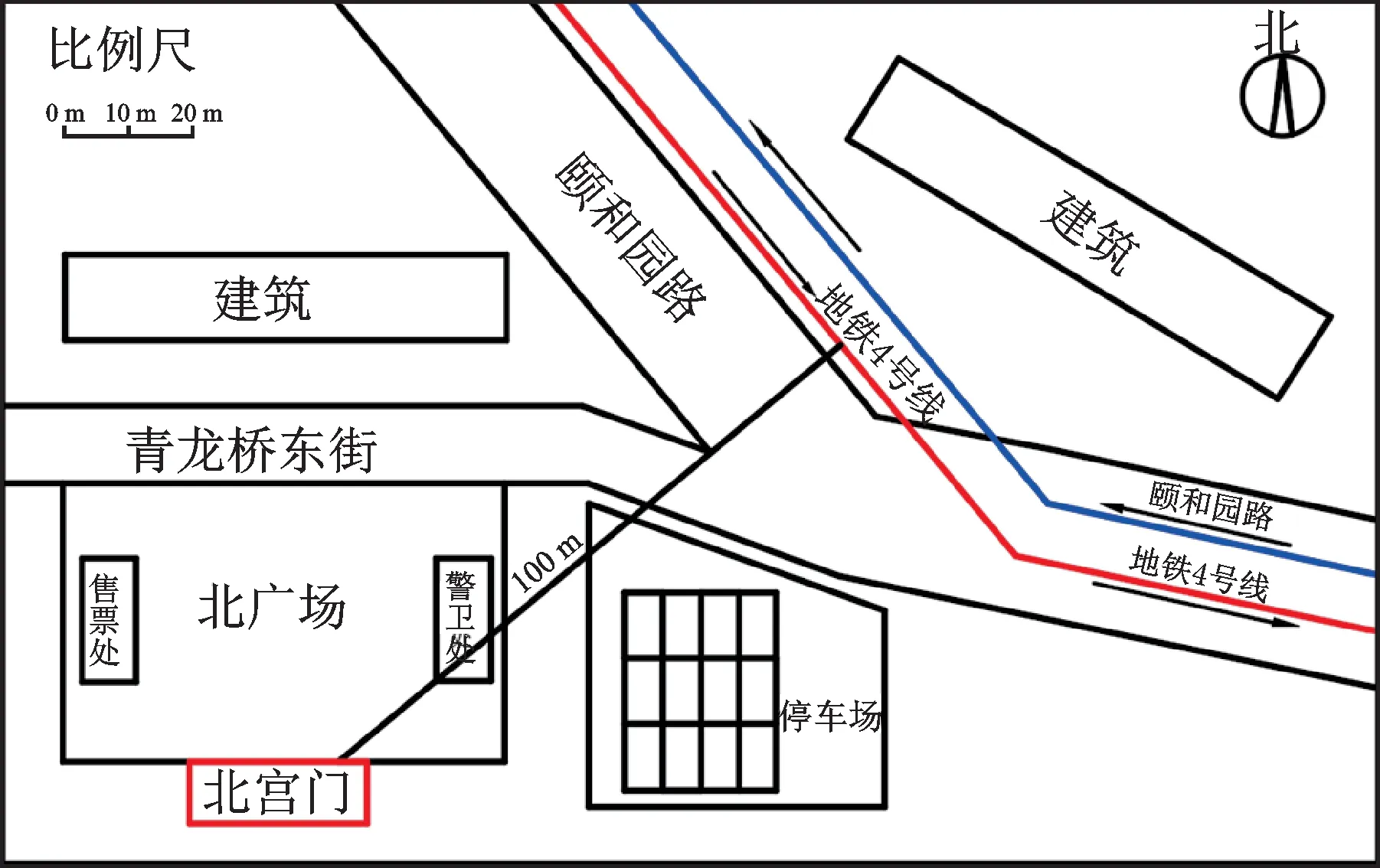
图5 北宫门附近场地平面示意图Fig.5 Schematic diagram of the site near the North Palace Gate
2 有限元模型建立
2.1 模型的建立
利用ABAQUS 有限元软件,建立如图6 所示的结构-隧道-列车振动耦合模型。北宫门结构根据图1~4 建立,对结构进行适当简化,忽略一些非受力构件(如砖砌体)并转化为对应荷载施加到相应构件上。结构主体模型中梁、柱、枋均采用梁单元(单元类型B32)进行模拟,楼板和屋面采用壳单元(单元类型S4R)进行模拟,础石采用实体单元(单元类型C3D8R)进行模拟,网格尺寸近似为0.2 m。
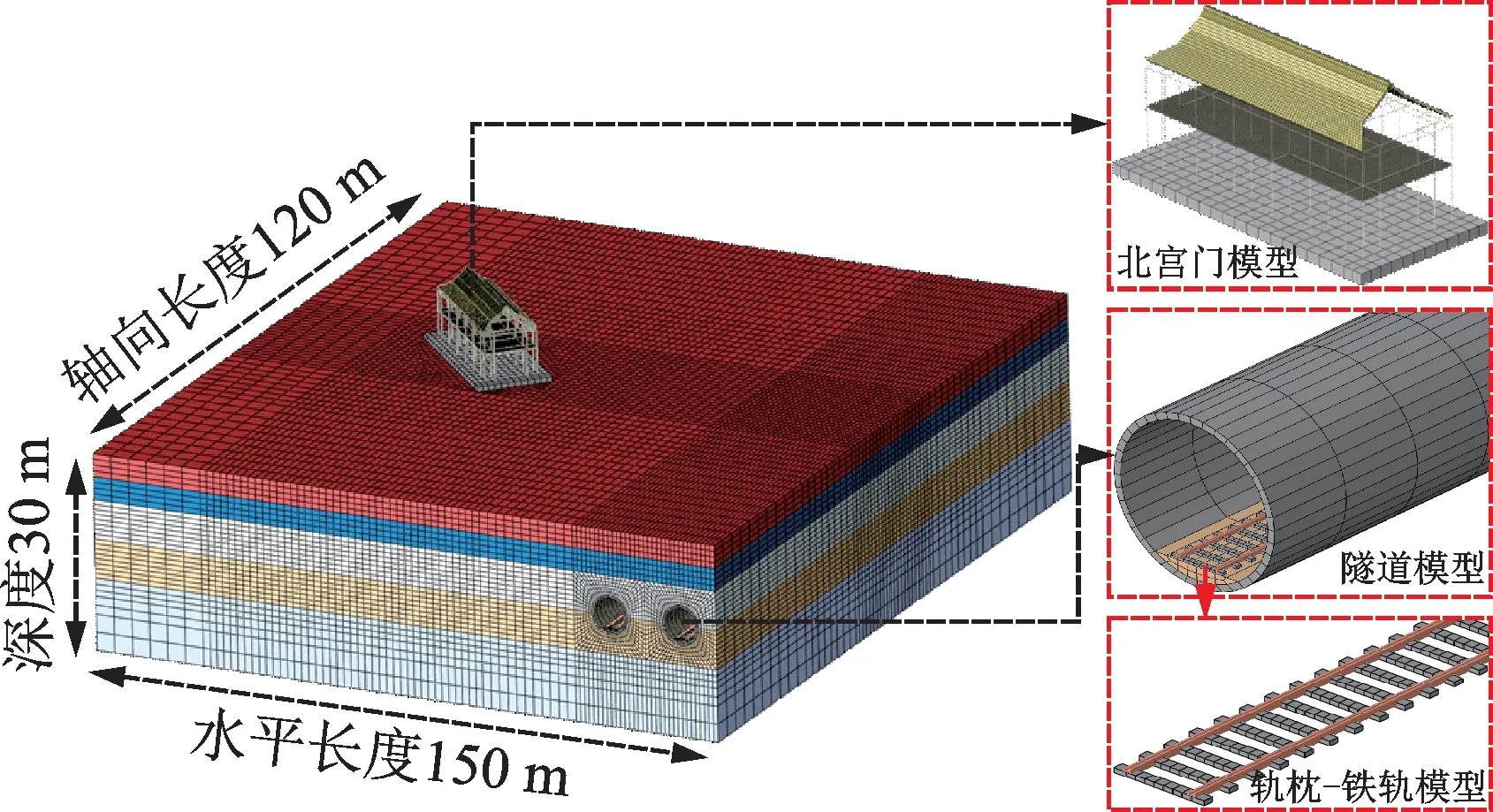
图6 结构-隧道-列车振动耦合有限元模型Fig.6 Structure-tunnel-train vibration coupling finite element model
隧道、道床与轨枕均采用实体单元进行模拟,网格尺寸为0.2 m;其中,隧道内径为5.4 m,外径为6 m;钢轨为T60 型,截面特性参数参考标准[17]选取,模型采用对应各部分尺寸的“工”字形截面梁单元进行简化模拟,详细参数输入如图7 所示,单向两轨间距d=1.435 m;轨枕的采用Ⅱ型钢筋混凝土轨枕,并将其近似为2000 mm×170 mm×200 mm 的长方体。

图7 铁轨截面及工字梁参数输入(单位:mm)Fig.7 Rail section and I-beam parameter input(Unit:mm)
土层有限元模型尺寸为30 m(垂向深度)×120 m(轴向长度)×150 m(水平宽度),水平方向上模型的长度大于10 倍的隧道直径,可获得较高的计算精度,降低边界效应[18]。单元类型选用C3D8R 单元,模型单元尺寸为0.3~2.5 m。本文的土层介质参数参考文献[19]中北京海淀区典型地质参数,其中的最小剪切波速为Vs=215 m/s。根据Yang等[20]的研究结果:用λsmin表示所关注振动波的最小剪切波波长,当单元长度取时,便已经可以取得较高的精度。此外,在列车运营环境下,振动对古建筑结构有显著影响的频率范围为0~50 Hz,进而得到适宜的网格尺寸为为保证精度的同时,节约计算成本,将隧道附近和北宫门附近的网格加密,最终场地的单元尺寸为0.3~2.5 m。
2.2 材料参数
北宫门结构所用木材为松木,根据《木结构设计标准》GB 50005—2017[21]和赵均海等[22]对木材参数的取值要求,确定落叶松新材的物理力学性质参数。考虑到北宫门修建距今已超过100 年,又根据《古建筑木结构维护与加固技术标准》GB/T 50165—2020[23]中建议的折减系数要求,将对应材料的弹性模量与剪切模量给予0.85 的折减调整,最终确定木材的力学参数如表1 所示。不同方向的弹性模量和泊松比利用ABAQUS 中的ENGINEERING CONSTANT 定义。场地土层参数同样参考2.1 节中提及的海淀区典型地质参数,简化后如表2 所示。北宫门石砖基台物理参数如表3 所示。隧道、道床、轨枕以及轨道的材料参数设置如表4 所示。北宫门结构阻尼比取0.035,土体阻尼比统一取0.05,均采用Rayleigh 阻尼设置单元的阻尼参数。

表1 木材材料参数Tab.1 Wood material parameters
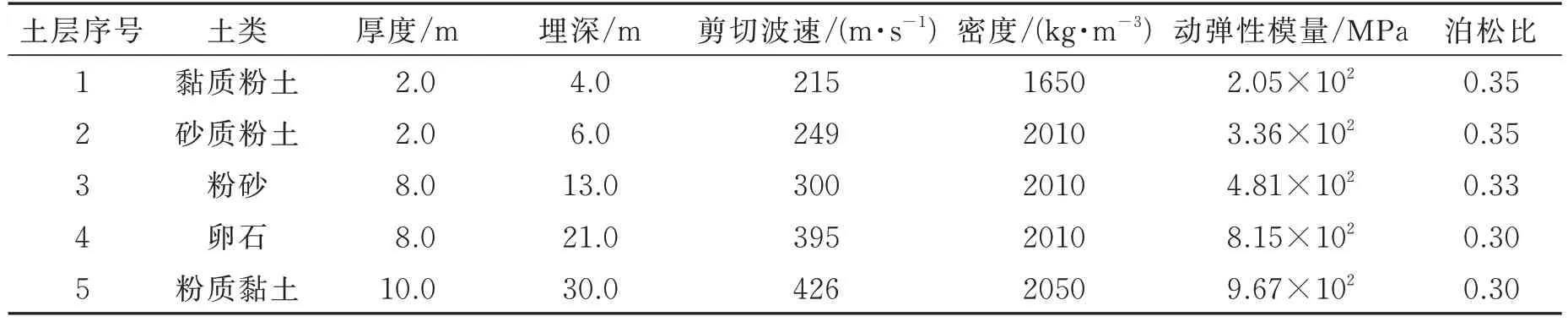
表2 土层材料参数Tab.2 Soil material parameters

表3 石砖基台物理参数Tab.3 Pahsical parameters of stone brick abutment
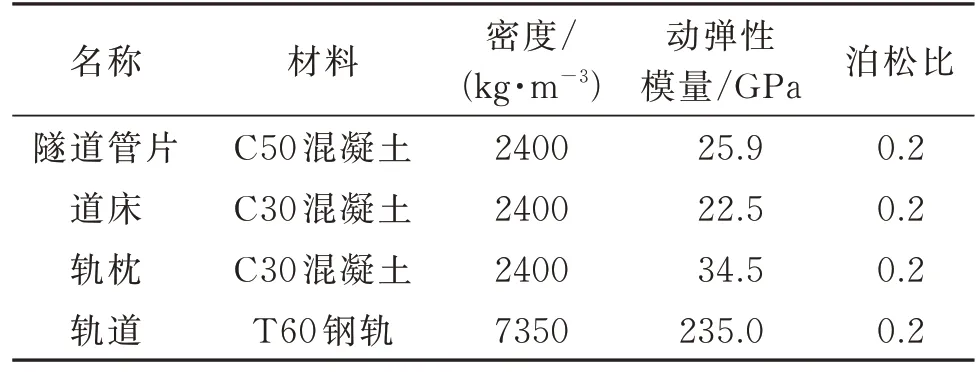
表4 隧道、道床、轨枕及轨道材料参数Tab.4 Tunnel,track bed,sleeper and track material parameters
2.3 接触条件
土体与隧道间采取面面接触的形式(Surface to Surface Contact),法向采取硬接触(Hard Contact),切向采取罚函数(Penalty)模拟,摩擦系数取为0.85;道床-轨枕-轨道间采取绑定约束(Tie)。
北宫门结构自身需考虑斗拱、梁柱榫卯节点、柱础与基台之间的连接设置。如图8 和9 所示,梁柱卯榫节点与斗拱节点保存的较为完好,均可视为中国古典建筑典型的半刚性连接方式,实施时采用CONNECTER 单元对斗拱和榫卯节点进行模拟。节点刚度根据文献[24]确定,如表5 所示。柱脚与础石参考文献[25]的处理方法,将柱脚与础石的连接节点近似简化为铰接节点。

表5 柱-梁、柱-枋和斗拱节点刚度参数设置Tab.5 Stiffness settings of beam-column tenon and dougong nodes

图8 北宫门木结构中的斗拱节点Fig.8 Dougong nodes in the wooden structure of the North Palace Gate

图9 北宫门木结构中的榫卯节点Fig.9 Mortise-tenon joints in the wooden structure of the North Palace Gate
2.4 边界条件
土体模型采用黏弹性边界削弱土层模型的边界效应,提高耦合模型的计算精度并降低计算的收敛难度[26]。具体实施时,通过对ABAQUS 软件进行二次开发,运用Python 编程输入每层土参数(密度、剪切波速和压缩波速等)并计算每层土的弹簧刚度、阻尼系数以及单元影响面积,批量化自动设置各土层的弹簧阻尼器,添加黏弹性边界后的土层有限元模型如图10 所示。

图10 添加黏弹性边界后的场地土层模型Fig.10 Model of site after adding viscoelastic boundary
2.5 荷载的施加
北京地铁4 号线运营列车为A 型车,具体车辆轴距参数和物理参数如图11 与表6 和7 所示[27-28],列车速度约为60 km/h。

表6 地铁A 型车轴距参数Tab.6 Wheelbase parameters of Metro Type A car

表7 地铁A 型车物理参数Tab.7 Physical parameters of Metro Type A car

图11 地铁A 型车特征距离Fig.11 Characteristic distance of Metro Type A car
采用下式所示激振力函数[29]求得列车荷载:
式中F(t)为振动荷载;A0为车轮静载,A1~A3为因轨道不平顺而产生的列车动力荷载,计算方法如下:
式中M0为列车的簧下质量(一个轮对质量加两个转向架质量);ω1~ω3为对应以上三种振动附加荷载的圆频率,计算方法如下:
式中v为列车行驶速度。
式(2)和(3)中,Li和ai对应行车平稳性、作用到线路上的动力附加荷载和波形磨耗三种控制条件下的波长与矢高,根据中国地铁线路的轨道情况[30],分别取三种典型不平顺波长和相应矢高为:L1=10 m,a1=5 mm;L2=2 m,a2=0.4 mm;L3=0.4 m,a3=0.08 mm。
根据以上计算方法,并结合表6 和7 中的对应参数即可求得60 km/h 速度下列车单个轮载时程曲线,如图12 所示(时间间隔取5×10-3s)。并借助DLOAD 子程序实现荷载的移动施加。
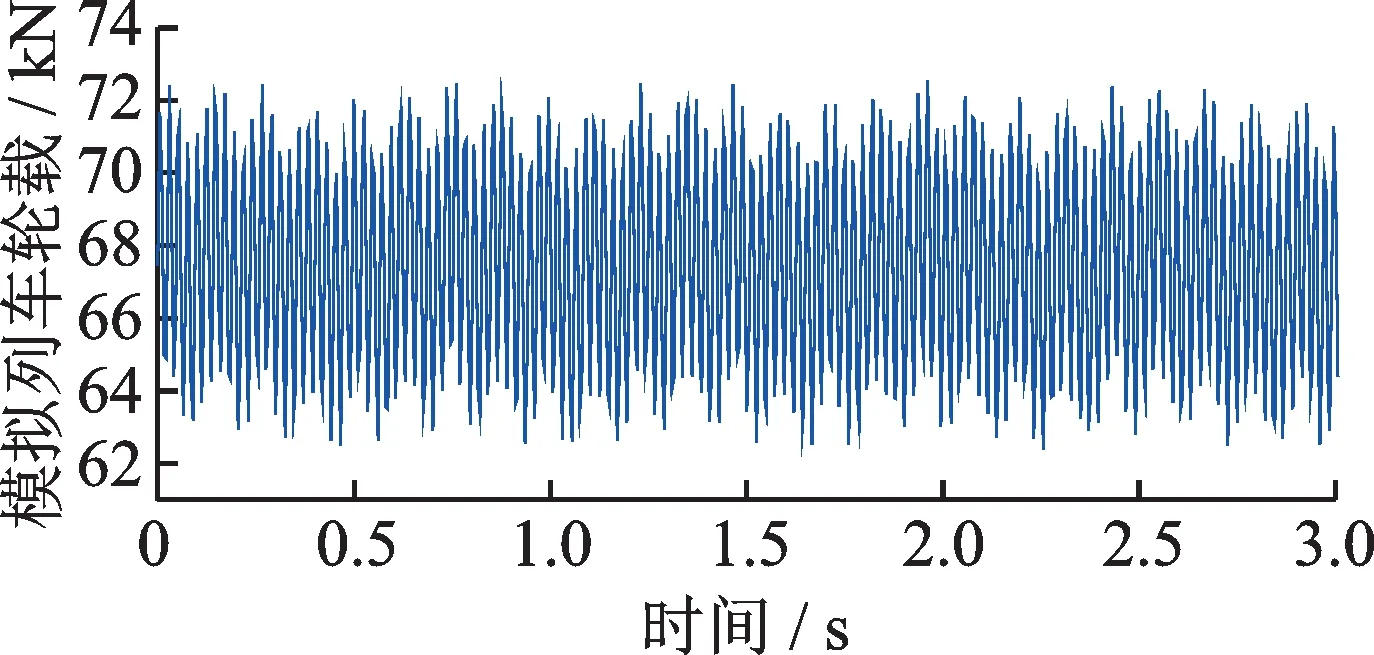
图12 60 km/h 速度下模拟列车轮载时程曲线Fig.12 Simulated train wheel load time history curve at 60 km/h speed
3 实测结果与数值模拟对比验证
3.1 仪器介绍及参数设置
为验证所建立模型数值模拟结果的可靠性,对北宫门受地铁运行振动影响情况进行现场实测。测量仪器采用英国Guralp Systems 公司生产的CMG-5TCDE 强震仪搭配Scream 软件(可同时测量三个方向的振动加速度,最大采样频率可达到1000 Hz)与ART3 软件(可实现数据的实时操作以及滤波、幅值查看以及傅里叶变换等功能)。测试仪器与操作软件如图13 所示。

图13 CMG-5TCDE 一体化测振仪和ART3 软件Fig.13 CMG-5TCDE integrated vibration tester and ART3 software
根据参考文献[31]中的研究,列车运营环境下,振动对古建筑结构显著影响频率范围为0~50 Hz,属于低频振动。此外,由于数据离散时会产生频率混叠现象,根据奈奎斯特采样定理(当采样频率大于信号中最高频率的2 倍时,采样得到的数字信号就能够较为完整地保留信号的原始信息),将此次测试的采样频率定为200 Hz。
3.2 测点布置
为尽可能分析场地振动传播规律,场地测点布置如下:沿地铁-古建筑的线路上每隔25 m 布置一个测点,共5 个测点,并标记为0 m 测点、25 m 测点、50 m 测点、75 m 测点与100 m 测点,其中0 m 测点代表地铁线路正上方,100 m 测点非常靠近建筑基台,可作为振动由场地传至建筑前的状态参考。确定西北至东南方向为列车行驶方向(数值模拟列车也按此方向运行),不同测点同步测量,且为了保证水平振动参考量的一致性,仪器所记录的两向水平振动的方向统一以北宫门的建筑朝向(正南正北)为基准,整体场地测点布置情况如图14 所示。
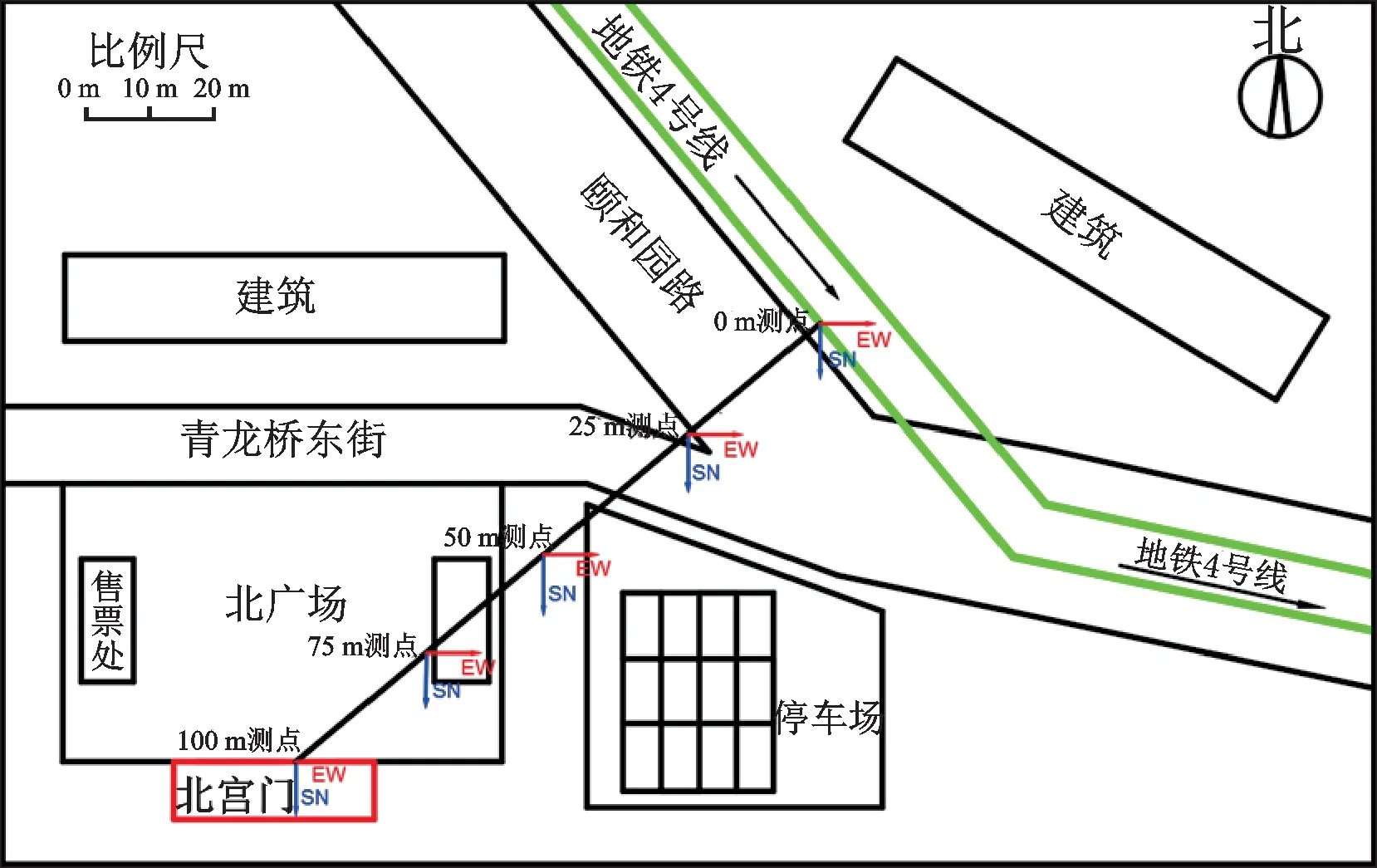
图14 现场测试采样点示意图Fig.14 Schematic diagram of sampling points for field test
结合文献[15]中对古建振动测量的相关规定,同时考虑到测试仪器的特性,古建筑木结构测点布置方案如下:在一层也就是建筑基台上,在北宫门东、西侧中央地面各布置1 个测点,同时在基台的四个角点附近各布置测点,以测量基台中央的振动量水平;在二层楼面上,在一层对应角点靠近柱的位置各布置1 个测点,以了解振动在建筑上垂直传播的规律,同时在二楼主室内靠东和靠西的楼板中央位置布置2 个测点。古建筑一、二层测点布置情况如图15所示。
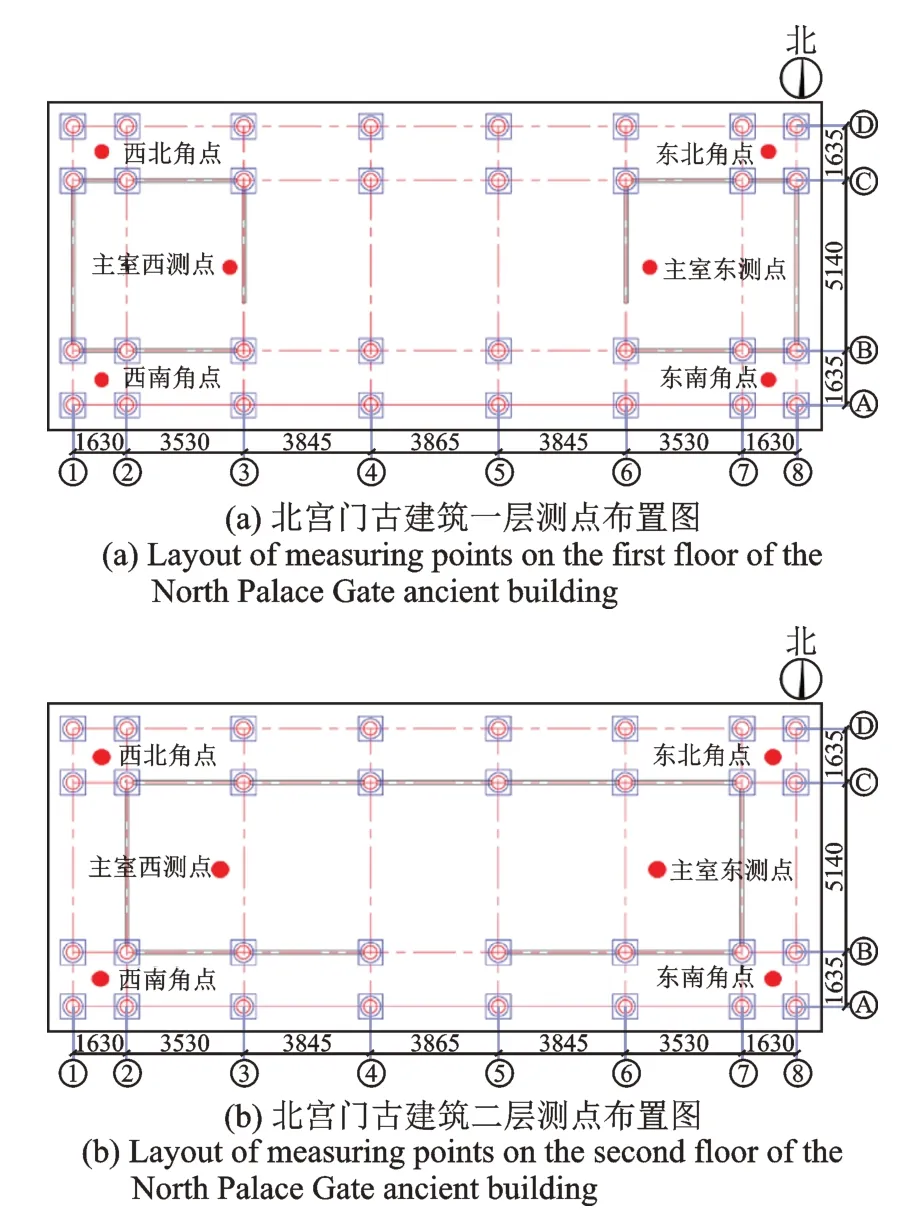
图15 北宫门测点布置图(单位:mm)Fig.15 Layout of measuring points of the North Palace Gate(Unit:mm)
3.3 结果对比
本文参考文献[15]的限值要求,对木结构的评估采用水平向速度半峰峰值进行评价,具体如表8所示。鉴于北京颐和园属于国家文物保护单位且北宫门所用材料为松木(弹性波速一般小于4000 m/s[32]),确定北宫门振动限值为0.18 mm/s。
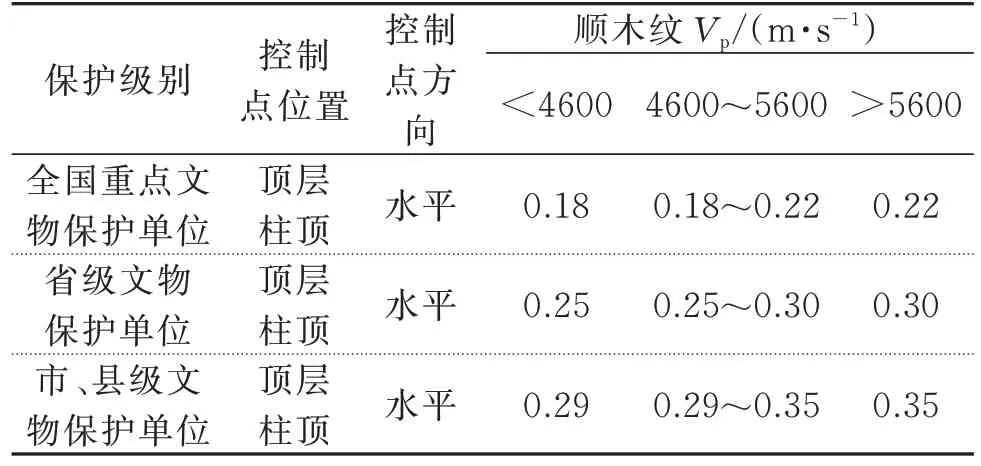
表8 古建筑木结构容许振动速度半峰峰值(单位:mm/s)Tab.8 Half peak value of allowable vibration velocity of wooden structure ancient building(Unit:mm/s)
3.3.1 场地反应
图16 给出了场地速度半峰峰值实测与数值模拟对比情况,对比振动量选取列车经过时段12 s 内的东西向和南北向水平振动的速度半峰峰值。

图16 场地地表模拟与实测速度半峰峰值衰减对比Fig.16 Comparison of the half-peak attenuation of velocity at the site surface simulation and actual measurement
对图16(a)和(b)进行分析可知,场地地表速度半峰峰值的模拟结果与实测结果衰减趋势大致相同,场地模拟振动强度值小于实测值,距地铁隧道较近处的误差值较大,0 m 拾振点的误差为22.47%,其余拾振点的误差均在10%~21%之间。这是由于0 m 与25 m 测点位于颐和园路的两端(见图14),背景振动测试结果较大导致实测结果与模拟结果的误差值比其他测点处的误差值大。
3.3.2 北宫门结构反应
(1)振动速度半峰峰值对比
建筑结构拾振点的振动速度半峰峰值模拟结果与实测结果对比如图17 和18 所示。由图17 和18 中数据可得,北宫门各测点振动速度半峰峰值最大为0.0893 mm/s,出现在二层东北角点位置,小于文献[15]中的限值要求,结构模拟结果与实测结果的误差在8%~25%不等,二层误差略小于一层。此外,模拟结果中的建筑各部分振动强度规律与实测大致相同,即二层振动强度大于一层,二层楼面振动强度是一层对应测点的2.3~4.5 倍左右;另外模拟结果中的建筑振动强度同样呈由东北侧至西南侧减小的趋势。
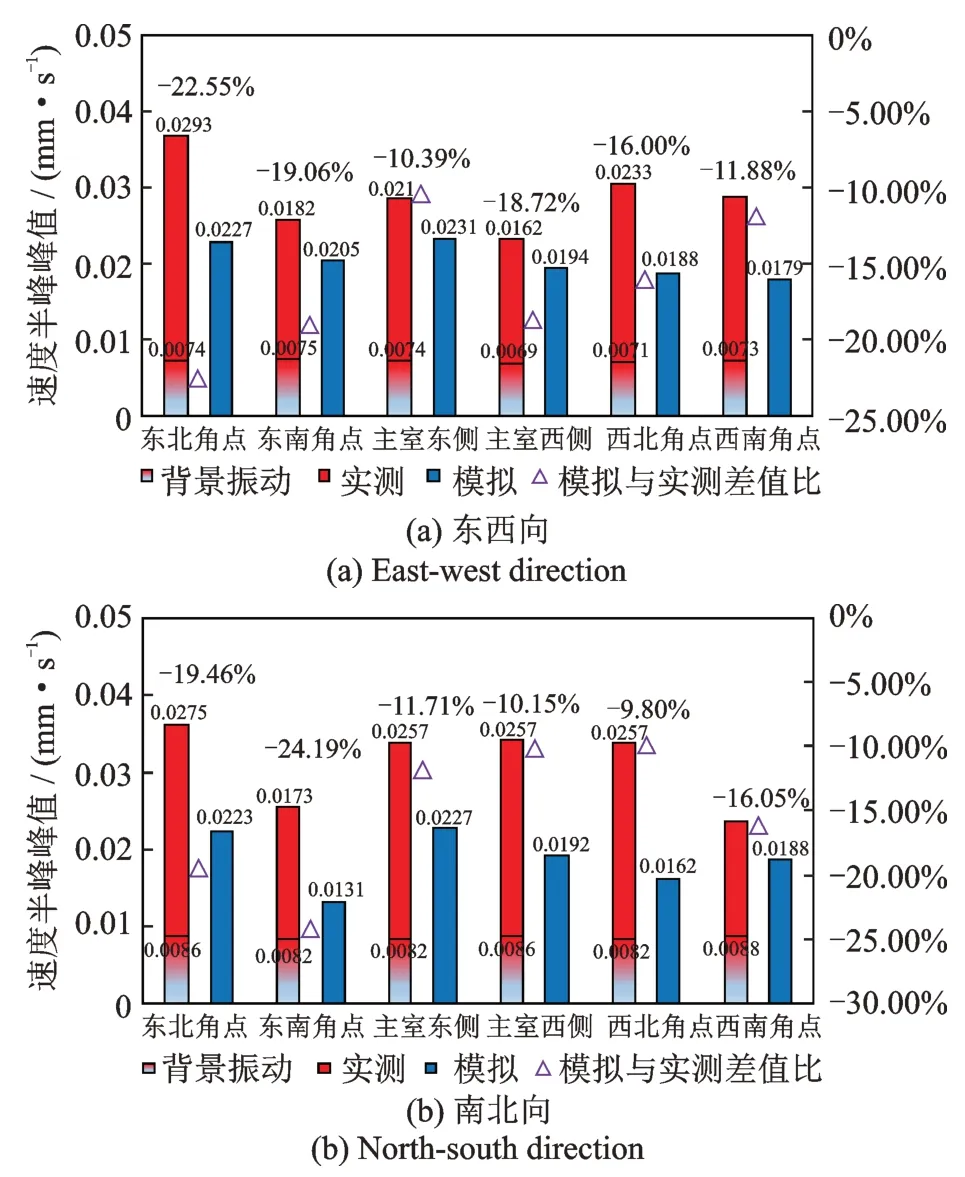
图17 一层各测点水平振动速度半峰峰值Fig.17 Half-peak value of horizontal vibration velocity at each measuring point on the first floor

图18 二层各测点水平振动速度半峰峰值Fig.18 Half-peak value of horizontal vibration velocity at each measuring point on the second floor
(2)频域对比
选择一层主室东测点和二层主室东测点进行频谱对比,结果如图19 和20 所示。

图19 一层主室东测点频谱对比Fig.19 Spectrum comparison of measurement points in the east side of main room on the first floor
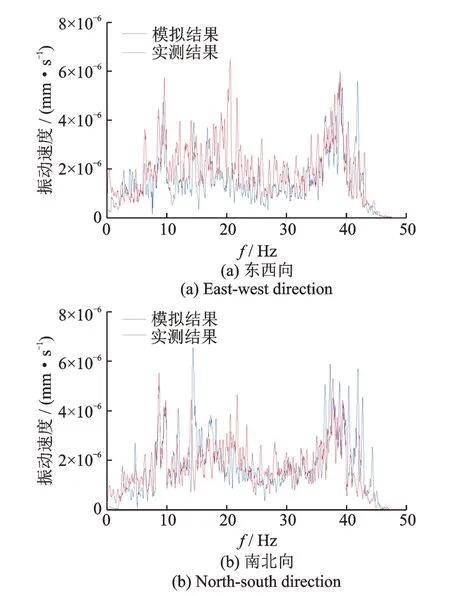
图20 二层主室东测点频谱对比Fig.20 Spectrum comparison of measurement points in the east side of main room on the second floor
从频谱图像间的对比可得,ABAQUS 有限元模拟所得到的振动频率与实测所得的振动频谱曲线走势一致,且主频率点差距不大。
通过上述对场地和北宫门结构的时域和频域振动响应对比分析可知,有限元模拟方法虽有一定的误差,但均达到了定性分析的要求,间接验证了隧道-土层耦合模型和采用激振力函数求得列车荷载以及DLOAD 子程序实现荷载的移动施加的合理性。分析误差原因主要是数值模拟不能考虑场地中受偶然因素影响较大的背景振动,而距地铁隧道较近处的场地振动响应受背景振动的影响较大。
4 数值模拟分析
本文采取单一变量法的思路,共制定如表9 所示的6 种工况,对建筑长轴与线路的夹角、列车速度进行参数化分析。
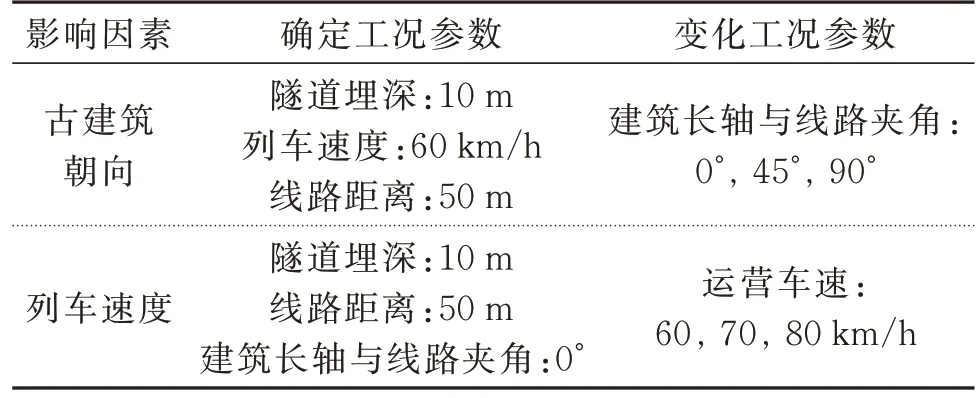
表9 古建筑地铁运营振动影响工况Tab.9 Working conditions of effects of subway operating vibration on ancient buildings
4.1 古建筑朝向
将模拟古建筑长轴与盾构隧道线路的夹角分别设置为0°,45°和90°,以研究建筑与地铁线路的夹角对结构振动的影响。采用设置局部坐标系的方式将输出结果转化成长轴x向、短轴y向的数据,同时计算合成向峰值,工况示意如图21 所示,计算结果如表10 所示。

表10 建筑长轴与线路夹角为0°,45°和90°工况各拾振点水平合成向速度幅值Tab.10 The horizontal composite peak value of the vibration speed at each pick-up point when the angle between the long axis of the building and the subway line is 0°,45° and 90°
观察表10,可发现三种夹角结构振动强度大小呈现如下趋势:0°夹角>45°夹角>90°夹角。同时,通过对比0°和90°工况下的振动幅值可以发现,不同夹角下,结构沿两主轴方向的振动强度差距有明显差异,具体表现为:当0°时,y向振动强度为x向的1.6~2.7 倍;当90°时,x向振动强度为y向的1.5~1.7倍。该现象的原因为:对于不同的振动波入射角度,结构所表现出来的振型特性有所不同。
另外,可以发现,三种角度工况下,各柱的振动强度基本遵循“近大远小”的规律,且振动最强烈的均为距地铁线路最近的拾振柱。例如:0°建筑长轴-线路夹角工况下,距线路最近的柱D4 振动强度最大,在45°和90°建筑长轴-线路夹角工况下,距离线路最近的柱C8 振动强度最大。该现象的原因为:振动传播过程中,场地振动强度随水平距离的增加而衰减,故距离线路较近的振动强度较大。
4.2 列车速度
将地铁列车速度分别取为60,70 和80 km/h,研究不同车速下结构的振动影响。本节以振动强度最大的柱D4 为例进行分析,图22 给出了三种速度情况下柱D4 的振动速度峰值。
由图22 可知,不同速度情况下,结构振动强度均沿结构高度逐渐增大。且随着车速的增加,各部分的振动强度均明显增大。以y方向为例进行说明:当列车车速为60 km/h 时,柱D4 二层柱顶振动峰值为0.1749 mm/s;车速为70 km/h 时,振动速度峰值为0.1888 mm/s,相对车速60 km/h 时增大幅度为7.95%;车速为80 km/h 时,振动速度峰值为0.2093 mm/s,相对车速60 km/h 时增大幅度为19.67%。
5 结论
本文以北京市地铁4 号线的振动对颐和园北宫门的影响为研究背景,首先将场地及北宫门的振动实测结果与有限元结果对比,分析了实际运行工况下场地振动衰减规律以及古建筑木结构的振动响应,保证了有限元分析模型精度。进而运用单一变量的方法,建立了不同建筑长轴与线路夹角、运营车速共6 种工况的有限元模型,系统地研究了不同影响因素对木结构古建筑振动响应的影响,得出以下结论:
(1)场地地表速度半峰峰值的模拟结果与实测结果衰减趋势相同,场地模拟的振动强度值由于未考虑背景振动的原因小于实测值,各拾振点的误差均在10%~23%之间。
(2)北宫门各测点振动速度最大值小于规范限值,建筑各部分振动强度规律的模拟结果与实测大致相同,建筑振动强度从东北侧至西南侧呈减小的趋势,二层楼面振动强度是一层对应测点的2.3~4.5 倍。
(3)地铁线路与临近木结构古建筑长轴方向夹角为0°时,结构振动强度最大,夹角为90°时,振动强度最小,且不同夹角下结构振动最强烈位置均出现在距地铁线路最近的结构柱位置,在对木结构古建筑维护检测时应重点关注。
(4)随着列车速度的增大,木结构古建筑的振动强度显著增大,与车速60 km/h 时相比,车速为80 km/h 时结构振动幅度增大19.67%。

