C/SiC 复合材料结构件热模态模型建模和修正方法
张昊冉,陈国平,2,何 欢,2
(1.南京航空航天大学航空航天结构力学及控制全国重点实验室,江苏 南京 210016;2.南京航空航天大学振动工程研究所,江苏 南京 210016)
引言
随着航空、航天等领域科学技术的高速发展,现有的高性能航空发动机涡轮进气端温度已经远远超过了高温合金的安全使用温度,因此必须开展新型耐高温材料的研究设计,才能满足航空发动机的要求。且新材料在满足耐高温的同时,还需要满足高比模量、高比强度以及耐腐蚀、抗氧化等要求。满足上述条件的C/SiC 复合材料将在未来广泛应用于航空发动机热端部件上[1-4]。C/SiC 复合材料在高温环境下尤其是1000 ℃以上的工作条件下依然可以保持很高的强度,但由于其结构相对于高温合金要复杂得多,表现出的力学性能也更为复杂。所以对于C/SiC 复合材料结构热环境下的结构振动特性分析和动力学模型的精确建立是很有必要的。关于高温环境下复合材料的有限元建模方法和优化方法,目前国内外学者已经做了大量研究[5-10]。张晓蕾等[5]建立了热环境下某型复合材料结构飞行器结构动力学计算的有限元模型,结合常温模态数据对有限元模型进行了优化,给出了较为合理的优化方法。杨浩[6]建立了C/SiC 典型结构件的有限元模型,采用弹簧单元模拟热应力影响,修正了典型结构在常温和高温下的模态频率。Battaglia 等[7]提出了一种基于振动数据识别任意形状、不同边界条件下正交各向异性板力学参数的方法,结合Rayleigh-Ritz 方法和粒子群优化方法来估计正交各向异性材料的弹性常数。
本文针对高超声速飞行器尾喷C/SiC 复合材料结构进行了常温、高温的模态试验。结合试验数据对结构自由模态、固支模态以及温度场进行修正,取得了良好的效果。通过修正结构中等效螺栓刚度以及弹簧单元刚度来模拟热应力影响,采用经典响应面法和牛顿迭代法对模型相关系数进行拟合和寻优,结果表明,此方法有显著的修正效果,修正后高温环境模态频率误差不超过0.5%,能够准确修正结构热环境下的复合材料参数及边界条件。
1 结构热环境振动理论和有限元方法
对于结构热环境振动问题,通常作出如下假设:热环境对结构振动特性的影响是单向的,即将热效应作为等效载荷作用于动力学方程。忽略由于结构振动引起的温度变化,材料始终处于弹性范围内,结构的应力-应变关系满足广义的胡克定律,结构的变形依旧是小变形,应变与位移关系中的二次微分项可以忽略不计。
热环境下结构的应力、应变以及温度三者关系在满足上面三个基本假设的基础上可以由杜哈梅-纽曼(Duhamel-Neuman)表达式给出:
式中βij为结构应变εkl=0 时测得的热模量;cijkl为一个对称张量;Θ表示结构的温度变化量,Θ=ΔT=T-T0。
对于含有对称面的各向异性材料,式(1)可简化为:
根据单位体积的应变能表达式可以得到由于温度变化产生的热应力,此时结构的单位体积的应变能为:
式中σ为热应力;ε为结构总应变;εT为结构温度变化引起的初始应变。
式(4)可化为:
从式(6)中可以发现,由于温度导致结构产生的热应力对结构的影响体现在后三项。利用弹性系数矩阵的对称性DT=D以及几何方程,对式(6)在整个单元上进行积分可以得到单元应变能为:
由式(7)可以看到,在热载荷引起的小变形下,几何刚度矩阵可以不予考虑,因此热载荷下的等效单元刚度矩阵可表示为:
在没有除热应力的其他初始预应力影响的情况下,单元初始刚度矩阵可写为:
式中Gij为变形梯度张量;ST=diag[SSS]为当前温度下的单元预应力矩阵,其中S为单元预应力在单方向上的分量。
根据单位体积的应变能表达式可以得到由于温度变化产生的热应力表达式,此时结构的动力学平衡方程为:
式中M表示质量矩阵;K=KT+Kσ,即为修正后的热刚度矩阵。
式(10)的解可以假设为以下形式:
式中φ为热环境下对应的振幅;ω为结构振动频率;θ为该解对应的相位角。
将式(11)代入式(10)得到矩阵K和M的广义特征值问题:
2 结构件热模态试验
陶瓷基复合材料的制备工艺采用化学气相渗透法(CVI),化学气相渗透工艺制备出的SiC 基体不仅具有良好的结晶性能、较高的强度和耐烧蚀等特点,且制备过程对碳纤维损伤小,因而制备出的陶瓷基复合材料性能更为优异。试验件纤维选用T700 6K PANCF 纤维,纤维外观为光滑圆柱体,横断面几乎是完整的圆形。主要性能参数如下:密度:1.76 g/cm3;拉伸强度:≥3000 MPa;弹性模量:≥200 GPa;纤维单丝直径:7.0 μm。预制体选用2D 针刺结构,采用一层T700 6K PANCF 无纬布与一层T700 12K PANCF 网胎交替铺层,无纬布为0°/90°铺层,1.X+2.Y方式连续针刺而成,如图1 所示。
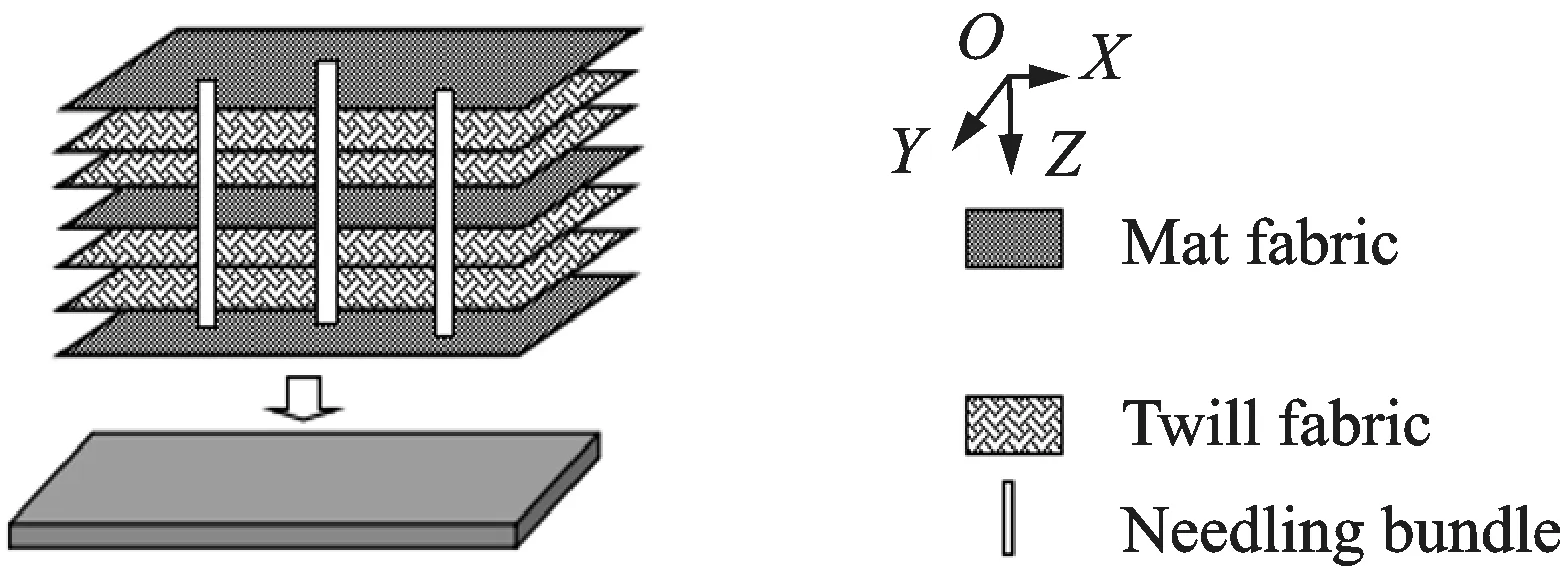
图1 试验件结构示意图Fig.1 Schematic diagram of structure of test piece
C/SiC 复合材料试验件长400 mm、宽30 mm、厚4 mm,肋板长160 mm、高8 mm、厚4 mm,中间有一V 型缺口,宽8 mm、深6 mm。示意图与实物图如图2 所示。

图2 C/SiC 复合材料试验件Fig.2 C/SiC composite material test piece
开展了常温环境试验件自由模态试验以及常温,400,800 和1200 ℃固支模态试验。自由模态将试验件用弹性绳吊装后用锤击法敲击获得,固支模态用激振器激励获得。采用高温加热炉进行温度加载,加热区域为C/SiC 复合材料试验件中段,加热时先将加热炉两端用堵头封住,当温度升高到指定温度时利用设计的滑轨放入试验件并固定,等温度稳定后获取结构振动特性。图3 和4 为固支模态试验示意图,表1 和2 分别为自由模态试验结果和固支模态试验结果。

表1 常温自由模态试验结果Tab.1 Free modal test results at room temperature
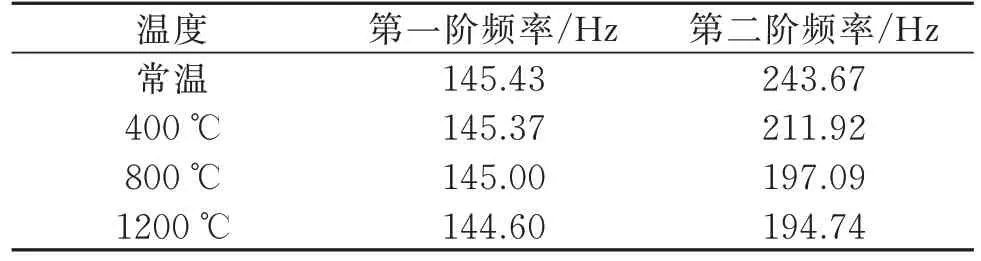
表2 常温和高温固支模态试验结果Tab.2 Results of fixed support modal test at room temperature and high temperature

图3 模态试验Fig.3 Modal test
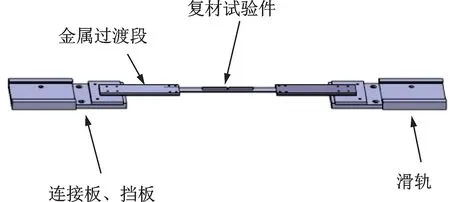
图4 试验结构示意图Fig.4 Schematic diagram of test structure
3 有限元模型的建立与修正
3.1 模型建立
本文在MSC.Patran 软件中建立的C/SiC 热模态试验数值仿真模型如图5 所示。为准确计入金属夹持段刚度对试验结构动态响应的影响,在整个数值模型中包括了金属夹持段模型。螺栓采用beam单元和RB2 进行模拟,采用6 自由度弹簧单元模拟金属夹持段与试验件之间的连接刚度,金属夹持段与刚性约束之间的连接采用同样的处理方式。

图5 C/SiC 试验件及金属夹持段模型Fig.5 C/SiC test piece and metal clamping segment model
3.2 模型修正
C/SiC 试验件由快速CVI(化学气相渗积法)制备而成,其结构尺寸以及内部纤维分布存在一定分散性;常温和高温环境下复合材料的力学性能试验结果表明复合材料的力学性能具有较大分散性[11-12]。固支约束在高温环境下由于材料热膨胀系数的不同会在结构内部产生热应力。材料内部结构和力学性能的分散性以及热应力都会影响结构的动力学特性。所以本文按照由简单到复杂的顺序,以常温自由模态、常温固支模态和高温固支模态的修正顺序对材料的力学性能、热学性能、结构尺寸以及固支边界约束刚度进行修正。模型修正总体思路:首先通过模态频率对结构参数的灵敏度进行分析,确定主要的频率影响参数;然后拟合频率与影响参数的关系;最后结合优化算法获取最优解,完成模型修正。当有温度作用时,首先通过实验实测温度场对计算温度场进行修正,再对模态数据进行修正。修正计算流程如图6 所示。

图6 模型修正计算流程Fig.6 Calculation process of model modification
影响C/SiC 试验件自由模态频率的参数主要有材料拉伸模量、剪切模量和泊松比等。以常温下自由状态的模型为研究对象对参数进行灵敏度分析,其中关于灵敏度的表达式如下:
式中Se为灵敏度矩阵;Δf为频率残差向量;Δp为修正参数摄动量百分比。
将上述修正参数摄动量取为5%,分别计算前三阶频率对各参数的灵敏度,表3 为参数值单位百分比变化引起的前三阶频率变化。由表3 可知,材料X,Y方向拉伸模量、面内剪切模量以及试验件厚度对前三阶弯曲自由模态频率的影响较大,将其作为自由模态模型修正的优化参数,材料拉伸、剪切模量取值范围通过材料制备时测得的参数值确定,如表4所示。

表3 各参数前三阶自由模态频率灵敏度(单位:Hz)Tab.3 The first three order free modal frequency sensitivity of each parameter(Unit:Hz)
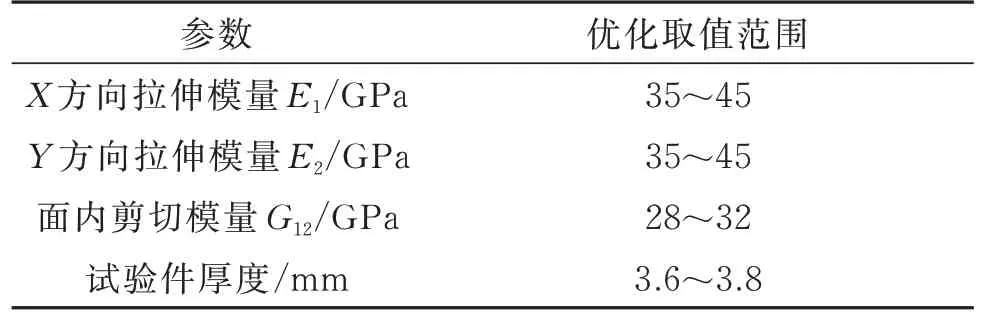
表4 自由模态修正参数取值范围Tab.4 Value range of free modal correction parameters
修正参数的优化表达式为:
式中F为目标函数;αi为权重系数为模态试验频率;fi为模型计算频率;i为模态阶数;X为优化参数;XU,XL分别为优化参数的上/下限。
本文采用经典响应法建立计算频率、优化参数以及试验频率之间的关系,通过牛顿迭代法进行迭代修正,由优化表达式(14)得到修正结果。
牛顿迭代法基于二阶泰勒级数展开求解优化目标函数F(x)的二次近似驻点,迭代表达式可定义为:
式中Ak为优化目标函数泰勒级数二次项系数;gk表示目标函数在k处的梯度。
3.3 常温自由模态修正
基于复材试件自由模态试验数据,采用3.2 节所述方法,得到计算频率和X,Y方向拉伸模量、面内剪切模量和试验件厚度的关系,并计算得到各数据点拟合误差如图7 所示,拟合相关系数如表5 所示。优化表达式中的权重系数分别取α1=α2=α3=,对X,Y方向的拉伸模量、面内剪切模量和厚度进行修正。修正前后频率、模态频率误差和修正参数分别如表6,7 和8 所示。

表5 自由模态前三阶计算频率拟合相关系数Tab.5 Correlation coefficients fitting of first three order calculation frequencies of free modal

表6 修正前后自由边界模型模态频率结果Tab.6 The modal frequency results of the free boundary model before and after modification

表7 修正前后自由边界模型模态频率误差Tab.7 The modal frequency error of the free boundary model before and after modification

表8 修正前后模型参数Tab.8 Model parameters before and after modification
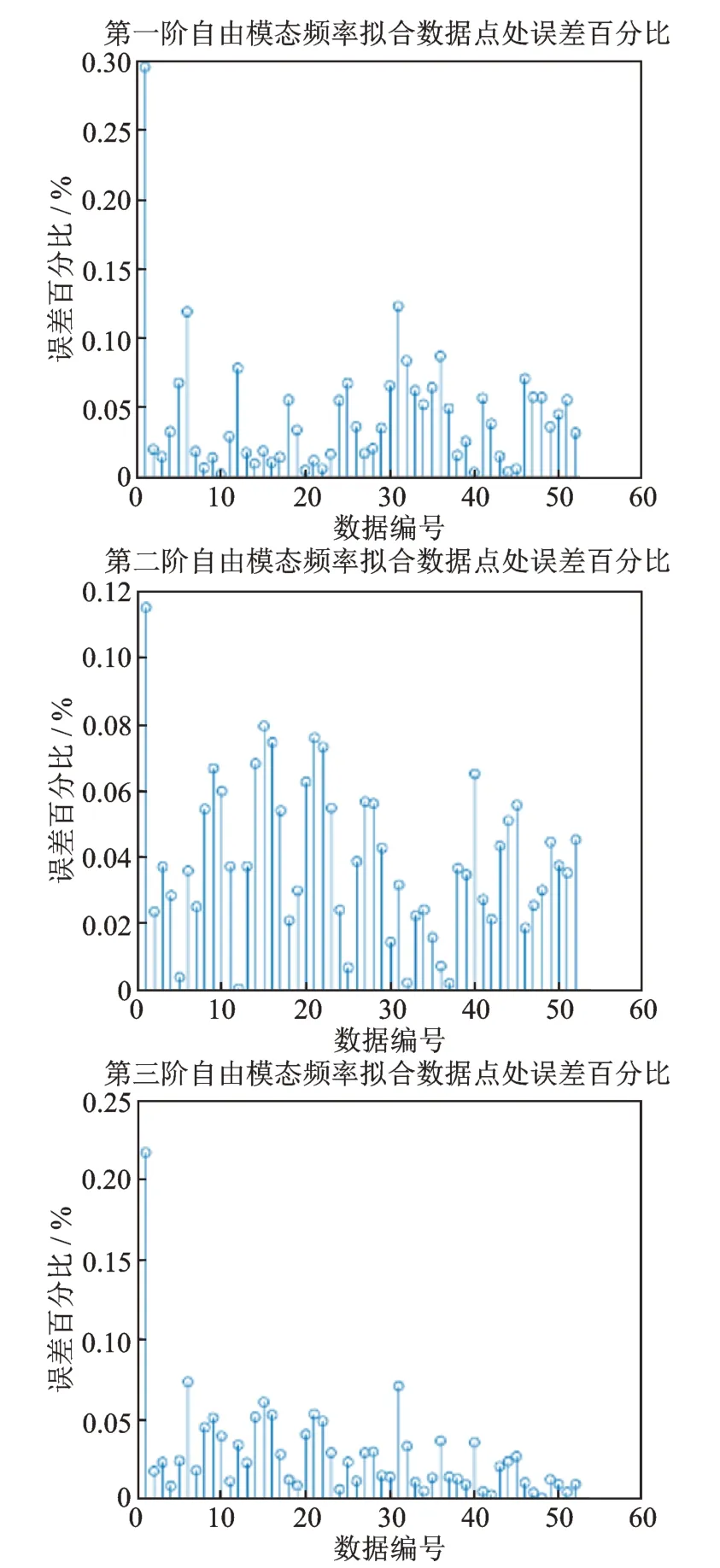
图7 自由模态前三阶计算频率拟合数据误差Fig.7 The first three orders of free modal calculation frequency fitting data error
采用全局近似模型建立前三阶自由模态频率与X,Y方向拉伸模量、面内剪切模量和试验件厚度的函数关系后,通过牛顿迭代法寻找函数二次近似驻点,确定寻优方向并进行迭代得到使优化目标函数达到最小值的结果,迭代过程中的误差收敛结果如图8 所示,自由模态修正误差在10 次迭代内收敛于1×10-7,满足误差收敛精度要求。
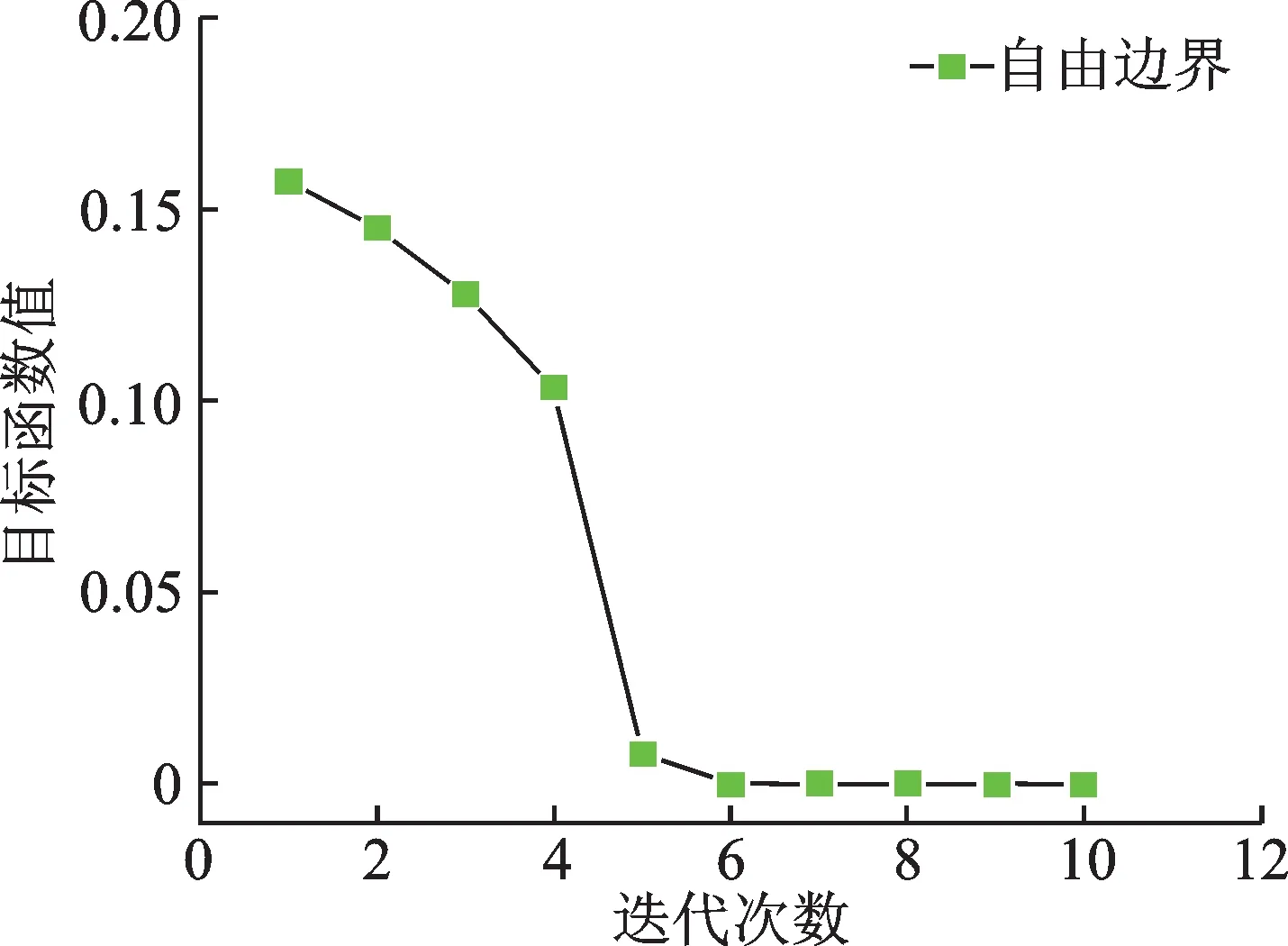
图8 自由模态优化目标函数值收敛曲线Fig.8 Convergence curve of free modal optimization objective function value
模态振型的相关性通常用振型的MAC 矩阵表征,表达式如下:
式中Φi与Φj分别为振型矩阵的第i阶与j阶向量。修正后自由模态振型与试验振型的MAC值(5个测点)如表9 所示,表明经过修正后前三阶模态振型相关性较好,修正后的模型接近真实模型。

表9 修正后自由模态振型与试验振型的MAC 值Tab.9 The MAC values of the modified free mode shape and the test mode shape
对比修正前后模态频率和MAC值发现前两阶模态的修正结果较好,由表7 可知修正前后频率误差减小,第一阶频率误差由10.62 Hz 下降到0.02 Hz,下降了6.09%;第二阶频率误差由39.97 Hz 下降到4.48 Hz,下降了9.57%;而第三阶频率误差由67.66 Hz 下降到21.53 Hz,下降了5.94%。修正后第三阶自由模态频率仍存在2.74%的误差,分析原因可能有:自由模态试验本身存在误差,吊装后敲击时弹性绳发生晃动,采集数据时实验室有噪声影响等都会影响试验结果;由于试验件为二维编制结构,内部纤维分布存在一定分散性,导致其力学性能非均匀,使得某一阶模态产生偏差。
3.4 常温固支模态修正
两端固支模型固支点选在外侧8 个螺栓处。C/SiC 试件修正后常温弹性模量已由3.3 节给出,固支模型修正主要考虑螺栓连接刚度以及复合材料试验件与金属夹持段连接处Bush 单元刚度的影响,通过修正简化螺栓模型中梁单元材料的弹性模量改变螺栓连接刚度;通过修正简化螺栓模型梁单元弹性模量以及Bush 单元刚度以达到修正模态的目的。
参数优化的取值范围如表10 所示。

表10 固支模态参数优化取值范围Tab.10 Optimal range of fixed support modal parameters
计算频率和修正参数的函数关系如图9 所示。基于固支模态试验数据,采用3.2 节的方法,优化表达式中的权重系数分别取α1=α3=0.5,对简化螺栓模型中梁单元材料的弹性模量以及Bush 单元刚度进行修正。

图9 常温固支模态等效梁单元弹性模量以及Bush 单元连接刚度关系Fig.9 Relations of elastic modulus of equivalent beam element with fixed support modal at normal temperature and connection stiffness of Bush element
迭代过程中的优化目标函数值收敛结果如图10 所示。修正前后固支边界模型频率结果、频率误差和模型参数分别如表11,12 和13 所示。修正后固支边界计算振型与常温实测振型(3 个测点)的MAC值如表14所示。

表11 修正前后固支边界模态频率结果Tab.11 The modal frequency results of the fixed support boundary before and after modification

表12 修正前后固支边界模态频率误差Tab.12 The modal frequency error of the fixed support boundary before and after modification

表13 修正前后模型参数Tab.13 Model parameters before and after modification

表14 修正后固支边界计算振型与常温实测振型的MAC 值Tab.14 The MAC values of the calculated vibration mode of the modified fixed boundary and the measured vibration mode at room temperature
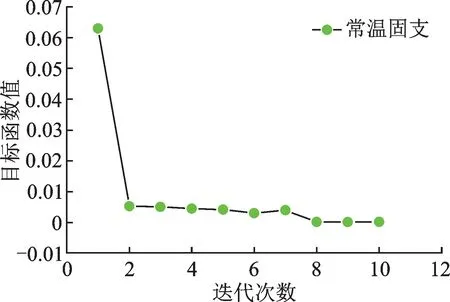
图10 常温固支模态优化目标函数值收敛曲线Fig.10 Convergence curve of optimization objective function value of fixed support modal at room temperature
对比修正前后模态频率和振型MAC值发现第一、三阶模态的修正结果较好,修正前后频率误差减小。由表12 可知,第一阶频率误差由2.32 Hz 下降到2.05 Hz,下降了0.19%;第三阶频率误差由2.58 Hz 下降到0.75 Hz,下降了0.75%。
3.5 高温固支模态修正
高温环境固支边界模型的修正主要考虑弹性模量随温度变化的影响以及热应力的影响。由于2D-C/SiC 复合材料在高温过程中发生腐蚀氧化,表面CVD 涂层中的微裂纹以及气相沉积法产生的内部缺陷使得氧化性气体能够扩散至材料内部,在高温环境发生振动时对内部C 纤维造成损伤,导致复合材料强度和弹性模量下降,影响结构模态。而由于试验加热区域只有C/SiC 复合材料试件中间部分,导致复材试件产生热变形,主要热变形方向为沿试件长度方向,使得在固支约束端产生热应力,对结构模态产生影响。
高温固支边界模型修正思路为:首先在有限元模型中施加与试验加载相同的温度,通过修正材料热传导系数以及和空气的热对流系数使得仿真温度场与实测温度场对应;再通过对复合材料试验件和金属过渡段内侧连接处等效螺栓连接刚度、C/SiC复合材料X,Y方向弹性模量进行修正,使计算频率与实测频率对应,达到修正模态的目的。
经过对仿真温度场的修正,三种温度加载情况下三个测点温度计算值与实测值相差不超过2.3%,结果表明修正后温度场与试验实际温度场近似相等,在有限元模型中用修正后温度场代替真实温度场进行加载。
基于固支模态试验数据,采用3.2 节的方法,优化表达式中的权重系数分别取α1=α3=0.5,对复合材料试验件和金属过渡段内侧连接处等效螺栓连接刚度、C/SiC 复合材料X,Y方向弹性模量进行修正。修正前后固支边界高温模态频率结果、频率误差和模型参数分别如表15,16 和17 所示。拟合误差如图11 所示。修正迭代收敛曲线如图12 所示。
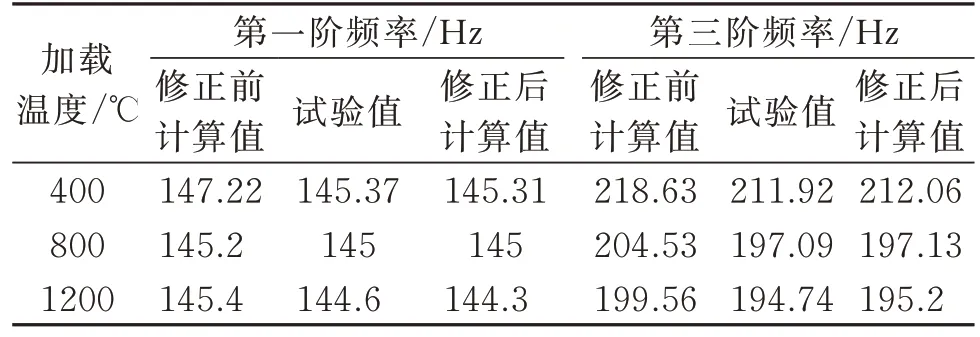
表15 修正前后固支边界高温模态频率结果Tab.15 High temperature modal frequency results of the fixed support boundary before and after modification
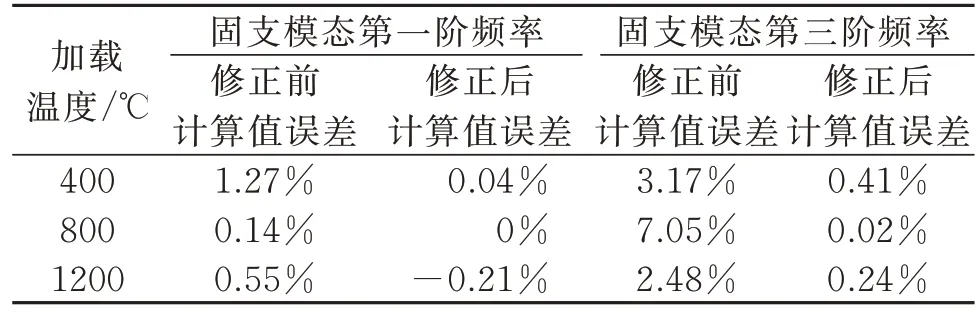
表16 修正前后固支边界高温模态频率误差Tab.16 High temperature modal frequency error of the fixed support boundary before and after modification
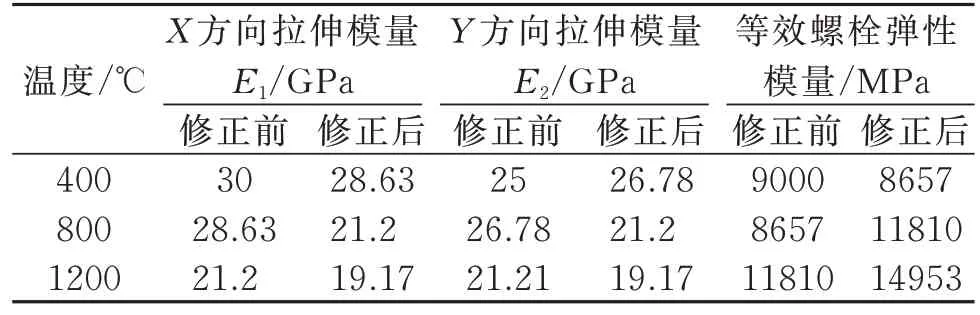
表17 修正前后模型参数Tab.17 Model parameters before and after modification
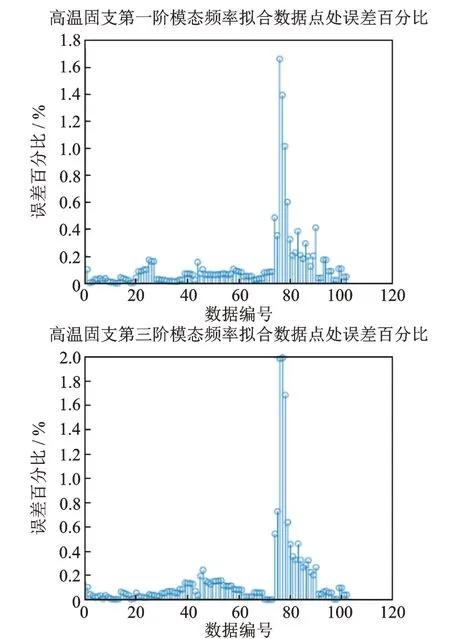
图11 高温固支第一、三阶弯曲模态计算频率拟合数据误差Fig.11 Errors of calculation frequency fitting data of the first and third order bending modals of fixed support at high temperature
由于高温试验传感器测点无法布置在高温区(C/SiC 复合材料试件),只在金属夹持段布置测点,无法测出结构完整振型,故高温修正后不计算修正后的MAC值。
对比修正前后固支边界高温模态频率结果发现,修正前后两阶模态频率误差均减小。随着加载温度升高,复合材料试件X,Y方向拉伸模量下降,等效螺栓刚度增大。修正后不同温度加载情况下第一、三阶固支模态频率误差都在0.5%以内。
4 结论
本文建立了考虑温度效应的C/SiC 复合材料结构的动力学有限元模型,提出了基于多层级思想的C/SiC 复合材料结构模型修正方法,以C/SiC 力学、热学性能参数以及等效螺栓连接刚度为修正变量,开展了模型修正。主要结论如下:
(1)在考虑温度效应的C/SiC 复合材料结构动力学有限元模型中,用梁单元和RB2 模拟金属夹持段螺栓连接,通过修正等效螺栓刚度可以有效模拟热应力影响。
(2)采用经典响应面法和牛顿迭代法对模型相关系数进行拟合和寻优,使有限元模型计算的模态频率与试验测得的模态频率结果相吻合,结果表明,此方法有显著的修正效果,修正后高温环境模态频率误差不超过0.5%,能够准确修正结构热环境下的复合材料参数及边界条件。

