全工况履带车协同天棚控制策略方法研究
李元芾, 邵昊南, 褚艳涛, 张会生
(1.上海交通大学 教育部重点实验室,上海 200240;2.中国北方车辆研究所,北京 100072)
在不同路面状况下行驶的振动控制是履带车辆整体性能的突破点,由路面激励引起的车辆振动和摆动的问题亟待解决,提高履带车悬架的控制效果至关重要.针对履带车在复杂地形上的振动控制,很多学者以车辆平顺性和安全性为指标进行了大量研究.曾谊晖等[1]开发了基于磁流变阻尼器的履带车辆半主动悬架智能复合控制系统.前馈控制方法为模糊控制,反馈控制方法是经典PID控制.于杨等[2]将最优控制理论与半主动履带式辅助车辆模型相结合,将悬挂系统置于正弦路面激励中,计算并比较前后控制系统之间的差异.阴运宝等[3]参考了线性二次型最优控制理论,为履带式车辆半车模型设计了主动悬架控制器,并分析了设计方案的有效性.
上述研究人员根据不同理论选择了半主动悬架控制系统并且能够实现振动平顺性的提升.然而,上述研究单独使用同一种路面或正弦路面,未考虑不同路面和不同速度下的激励影响,与实际情况不够符合;此外,实际履带车系统需要简单有效的控制模型来实现最好的控制效果,上述研究选取的控制策略过于复杂.因此,有必要采取新的控制策略并结合实际路面进行分析.
文中选取了一种在汽车中常用的天棚控制策略,并在6轮履带车动力学模型上完成了控制器的实现.同时,文中考虑了不同轮之间的协同控制,有效缓解了履带车辆的振动问题,提高了整车的平顺性,为履带车任务系统的控制提供了较好的控制基础.
1 天棚控制策略模型
1.1 天棚控制原理
悬架系统是履带式车辆的重要组成部分,其主要功能是减少从道路传递到车身的冲击载荷,减少车身振动,并确保车辆的驾驶舒适性.
悬架系统的天棚控制起源于汽车控制,其基本模型如图1(a)所示.为实现车身的振动控制,将天空视为固定不动的墙体,假设在车身与天空之间连接有一个阻尼器Csky,该阻尼器提供的阻尼力与车身的绝对速度成正比.EMURA J等[4]提出,上述假想的减振器可等效至簧载质量(车身)和非簧载质量(车轮)之间,原本处于该位置的减振器Cb等效为阻尼可调减振器Cbsky,如图1(b)所示.

图1 天棚控制原理
要实现减振器阻尼力的可调,将其阻尼元件改为可调式阻尼器.传统的机电式调节方法虽然能通过分级调节的方法适应不同的路面和工况,但其响应效果一般且结构较为复杂[5].采用安装电磁阀并控制其节流孔大小的方式进行阻尼调节,更能满足实际应用需求.
1.2 履带车天棚控制
目前的天棚控制器均以单轮为基础,传统的天棚控制使用如图1所示的单轮独立控制的方法,未将履带车系统考虑为一个整体.文中研究了履带车半车模型的天棚控制器的搭建,以某型号履带车辆为控制对象,控制的负重轮为第1轮、第2轮和第6轮.
采用天棚控制策略的1/2履带车主动悬架系统如图2所示,以下研究将以此模型为基础.其中:mb表示车身质量,θ表示俯仰角,I表示转动惯量;负重轮质量为mwi(i=1,2,3,4,5,6,下同);负重轮与路面间刚度为kwi;负重轮与车身质心之间的距离为li;车身与负重轮间刚度为kbi,阻尼为Cbi;假想的车身与天空之间的阻尼为Csky1和Csky2.此外,用Zb表示车身的垂直位移,Zwi与Zri分别表示负重轮和路面激励在垂直方向上的位移,v表示履带车水平方向的速度.
根据履带车辆悬挂系统的车体力学模型,得到系统的运动微分方程为

(1)

(2)
(3)
采用前文提到的假想减振器等效方法,将上述系统进行电磁阻尼等效.根据车辆实际情况,只有第1轮、第2轮、第6轮处可设置为可变阻尼,而其它三轮的阻尼为固定阻尼.用Ceq_sky1,Ceq_sky2和Ceq_sky6分别表示第1轮、第2轮、第6轮位置的等效阻尼,其余参数不变,得到等效后的天棚控制模型,如图3所示.
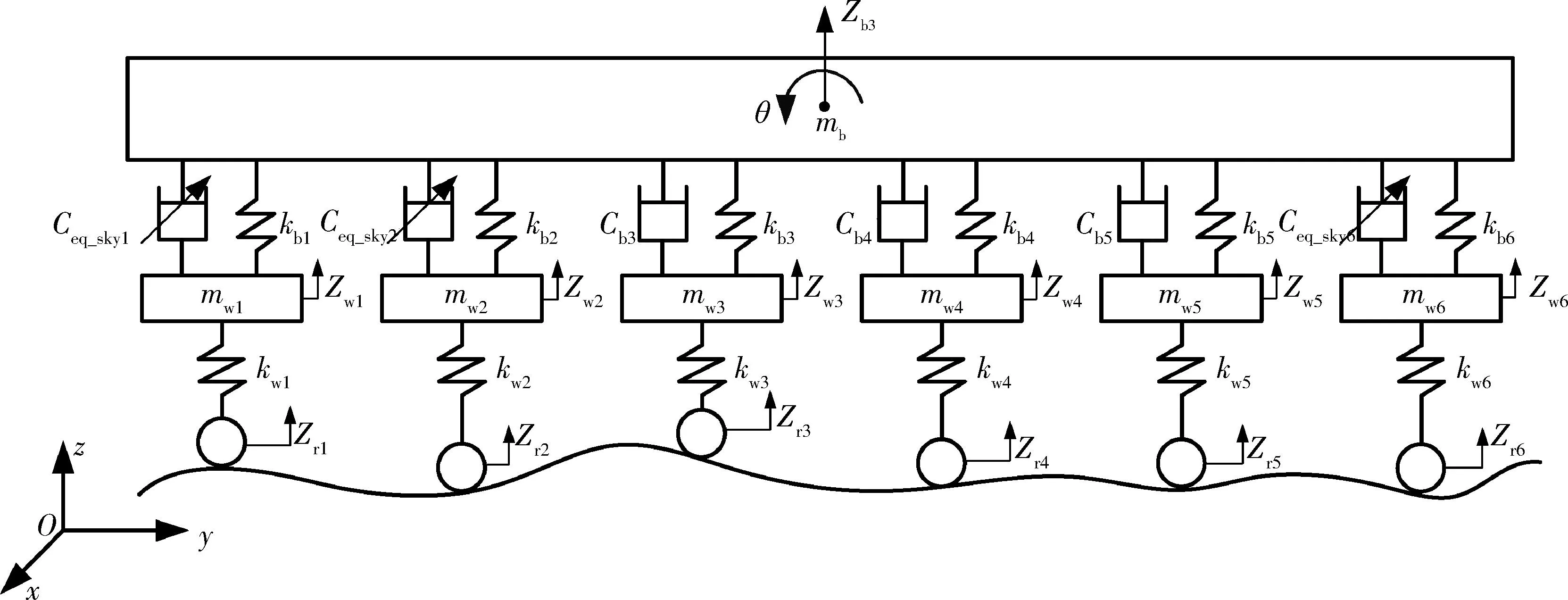
图3 等效天棚控制模型
根据履带车辆悬挂系统的车体力学模型,选择车身为研究对象,使车身的运动状态前后等效,得:

(4)
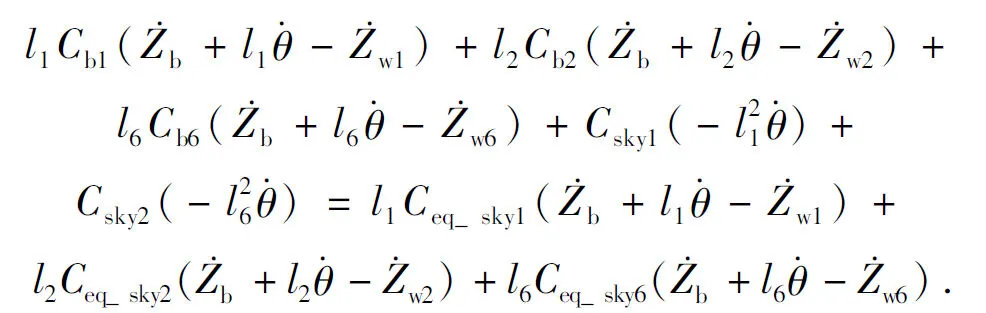
(5)
因此,在主动控制过程中,只需调整可变阻尼值,使之满足方程(4)和(5),即实现了履带车半车模型的天棚控制.
2 路面模型及车辆平顺性指标
2.1 路面激励源
使用环境的特殊性决定了履带车辆需要具有较高的行驶通过性和机动性,因此地面形貌对履带车辆性能有重要影响.
在道路工程中,不平度函数定义为道路纵向高度相对于参考平面沿道路方向的变化[6].这一概念在不同学科中也被称为路面轮廓曲线.为避免引起混淆,文中统一采用国标GB/T 7031-2005的定义,在下文中将不平度函数及其时域表达统称为路面不平度[7].本次研究作以下假设:履带车辆的行驶路面为无纵向变形的硬路面,即刚性路面,履带的碾压不会导致路面不平度发生改变,并且左右两侧路面的路面不平度函数一致;当路面波长小于履带节距时,因履带板的覆盖效果,路面不平度的影响基本可以忽略.
在系统研究中,考虑到路面不平度为随机过程,通常将其视为服从正态分布且均值为零的函数,其特性通过功率谱密度的形式进行描述[8].在本次研究中,采用谐波叠加法(或称三角级数法)构建路面不平度模型,即以离散谱对上述随机过程进行数值模拟逼近,通过傅里叶变换将随机信号分解为一系列正弦波或余弦波,并将不同频率和振幅的正弦波和余弦波叠加在随机相位上,以获得道路不平度的表示[9].
根据ISO标准,路面不平度的功率谱密度函数通常由以下拟合公式表示.
(6)
式中:n为空间频率;n0为参考空间频率(n0=0.1m-1);nl和nu分别为上、下限空间频率;Gq(n0)为参考频率n0下的空间功率谱密度;ω=2为频率指数[10].
考虑车辆行驶速度为u,将路面输入的空间频率功率谱密度Gq(n)转化为时间频率的功率谱密度Gq(f),得到时间频率为
f=u·n.
(7)
进而,时间频率的功率谱密度为
(8)
将空间频率区间nl和nu对应的时间频率(f1,fn)划分为N个小区间,用第i个小区间的中心频率fmid-1处的功率谱密度Gq(fmid-1)代替此小区间的功率谱密度,则第i个小区间的功率谱为
ωi=Gq(fmid-1)·Δfi.
(9)
根据功率谱ω与幅值谱A的关系式|A|=ω2,则第i个小区间对应的不平度幅值为
(10)
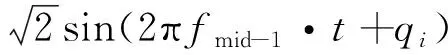
(11)
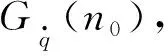

表1 不同等级路面功率谱密度
通过对实际道路的不平度测量,可知履带车辆行驶的典型路面覆盖了标准级路面C级至F级,因此,选取C级、D级、E级和F级路面作为地面形貌变量,据此研究路面不平度对履带车辆振动特性的影响.
运用MATLAB软件编程,由谐波叠加原理生成相应级数的功率谱密度值,并得到符合高斯分布的随机路面几何高程,空间频率范围为(0.011 m-1,2.83 m-1).
在MATLAB中仿真得出C级、D级、E级和F级路面不平度函数曲线.所构建的C级、D级、E级和F级路面如下图4所示.根据各个仿真工况的路长需求进行计算,合理选择道路的长度.过长的道路会增加仿真时间.
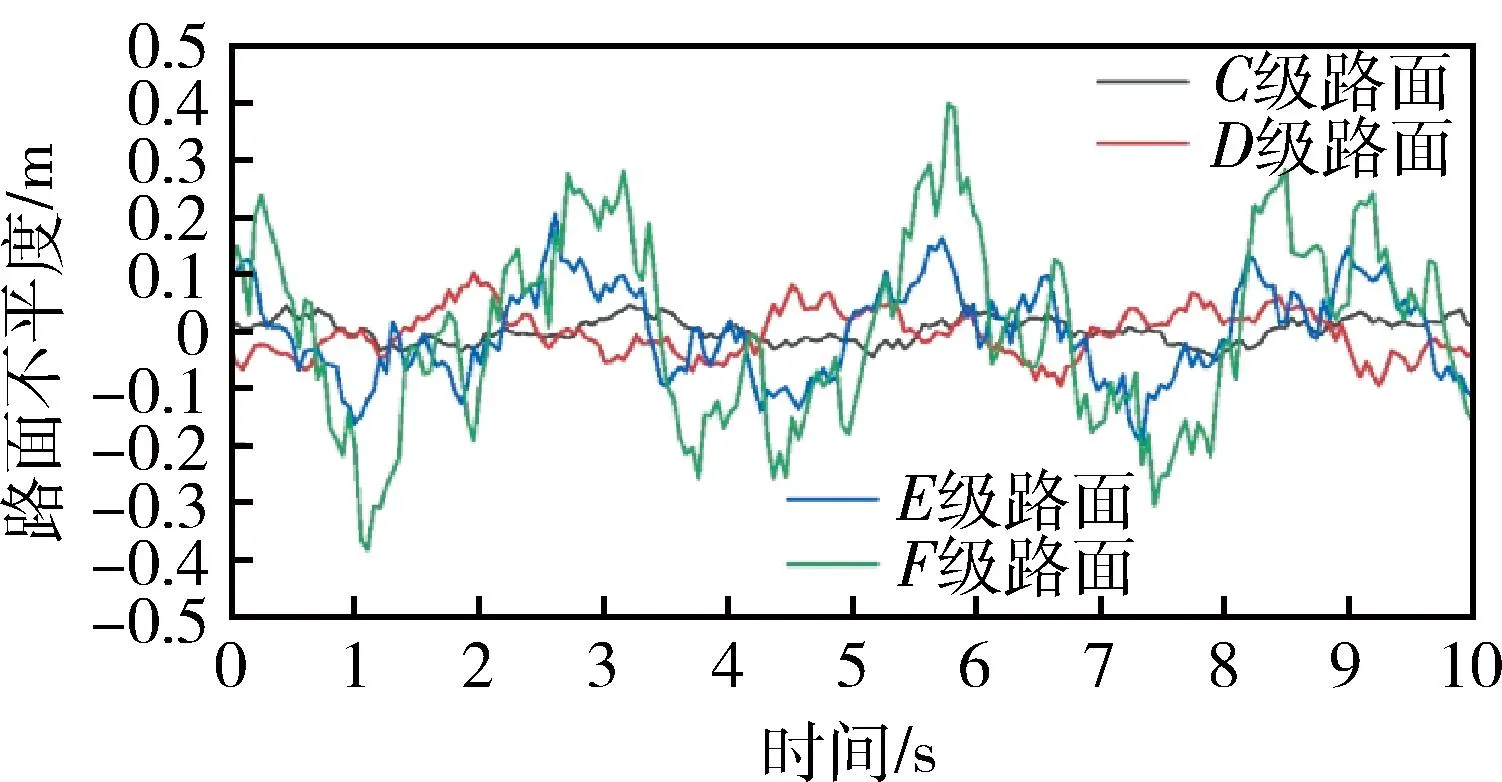
图4 路面激励源(30 km/h)
2.2 履带车控制指标
在悬架系统的控制器设计中,对悬架性能优劣有决定性影响的参数是悬架的刚度和阻尼.本研究中选择的控制指标为平顺性(乘坐舒适性).
簧载质量的加速度是一种被广泛认可的平顺性评价标准[11].具体而言,采用车体加速度的均方根(RMSE)值为指标,车辆的振动越大,对车内乘员的影响也越大.该值通常在驾驶员或乘客的座椅附近进行测量.在实际车辆中,悬架的工作空间是有限的.因此,若悬架振动幅度较大,达到其工作空间的极限,会与限位块发生碰撞,从而降低平顺性.而理论表明,较大的悬架动行程会快速耗散簧载质量的动能,从而减小其振动,提高平顺性.因此从上述两个方面看,提高平顺性和减小悬架动行程存在着矛盾.
一般而言,车辆平顺性通过车辆质心加速度和车辆质心处的俯仰角进行度量.目前大部分研究成果中采用下式所示的均方根值作为车辆平顺性的评价标准.
(12)
(13)

3 基于协同控制策略的履带车天棚控制效果分析
3.1 履带车及天棚控制的Simulink模型
基于控制模型与评价指标的分析结果,为研究天棚控制策略对全工况车辆平顺性的控制效果,在MATLAB/Simulink中搭建履带车悬挂模型.其中:车身质量mb=3×104kg;车身转动惯量I=2×105kg/m2;车身长度5 m;车轮等间距分布.弹簧刚度kbi=2.4 MN/m,(i=1,2,3,4,5,6);履带轮质量mwi=160 kg,(i=1,2,3,4,5,6);履带轮刚度kwi=48 MN/m.
在MATLAB/Simulink中建立模型,分为4个部分:第一部分是根据路面文件建立的路面激励输入;第二部分是建立的车体模型;第三部分是建立的车轮模型;第四部分是建立的第1、2和6轮上的控制器模型.应当指明的是,通过每个车轮之间路面激励的输入延迟确定车速的大小.其中,控制参数由粒子群优化算法(Particle Swarm Optimization,PSO)优化得到,第1轮、第2轮、第6轮位置的等效阻尼具体值Ceq_sky1、Ceq_sky2和Ceq_sky6分别为72 183.61 N/(m/s)、224 164.51 N/(m/s)、50 923.76 N/(m/s).
3.2 全工况平顺性控制效果分析
在工况选取方面,路面等级选取国家标准中规定的C级、D级、E级和F级,履带车运行速度选取典型运行车速30 km/h、40 km/h、50 km/h和60 km/h.平顺性指标选取车体竖直方向加速度均方根值(加速度指标)和车体角位移均方根值(俯仰角指标).在不同工况下,分别对采取文中的天棚控制模型前后的平顺性指标进行了测量和计算.
如图5所示,以E级路面为例,对比了采用文中控制策略前后,加速度和俯仰角指标的变化情况.横坐标为运行工况(道路等级和运行速度),纵坐标为平顺性指标.从图中可以看出,在不同工况下,两项平顺性指标在采用天棚控制后均得到了不同程度的提升,该控制策略能有效地提升履带车的平顺性.
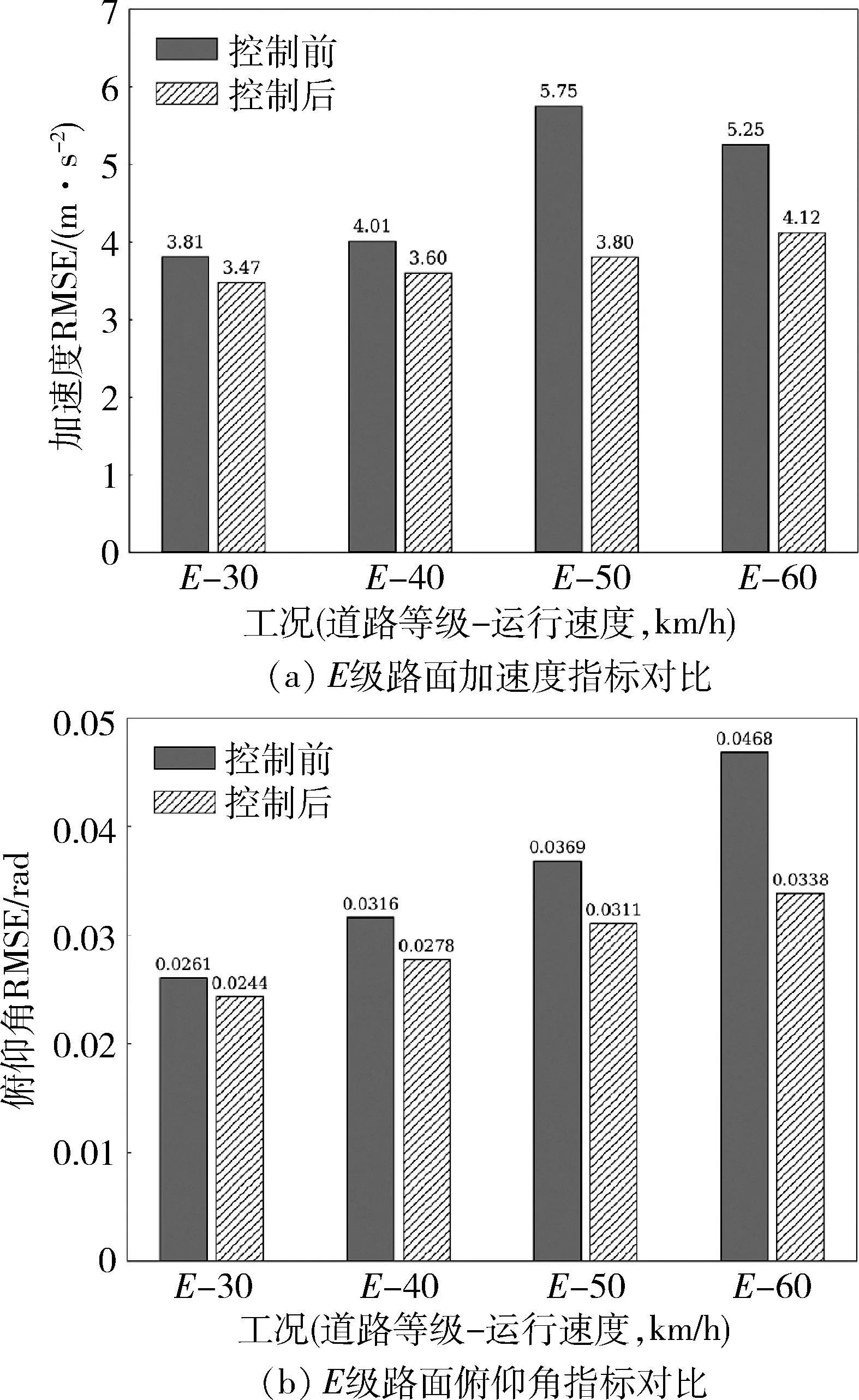
图5 采用天棚控制前后平顺性指标对比
采用文中控制策略后的不同工况下的加速度指标与俯仰角指标提升效果如表3所示,其中:V表示履带车运行速度.从结果中可以看出,在不同路面等级和运行速度下,加速度指标和俯仰角指标均有不同程度的提升.其中,当路面等级为E级、运行速度为50 km/h时,加速度指标提升最大,达到33.84%;当路面等级为C级、运行速度为60 km/h时,俯仰角指标提升最大,达到29.49%.在相同运行速度下,不同路面等级的平顺性提升效果相当;在相同的路面等级下,当车辆运行速度为50 km/h和60 km/h时,作为平顺性评价指标的均方根值较30 km/h和40 km/h更大,此时基于协同控制策略的履带车天棚控制方法对车辆平顺性的提升更为显著.上述结果表明,在不同工况下,采用同一种控制参数能够取得一定的效果,但部分工况下提升效果有限.要达成更好的控制效果,可考虑对不同的工况采用不同的控制参数.
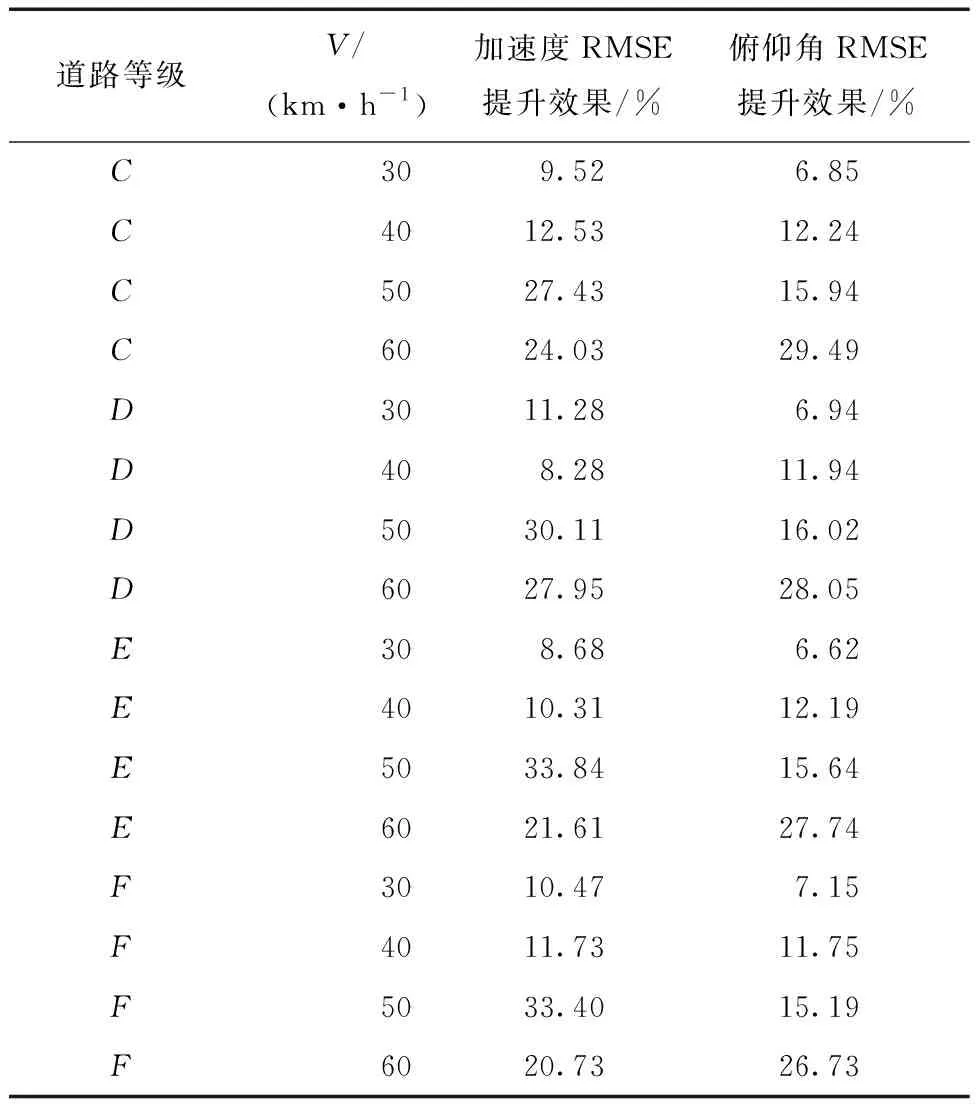
表3 不同工况下的加速度指标
以上分析均采用了不同工况下运行时间内性能指标的均方根值,为进一步说明主动悬架的控制效果,在时域对加速度指标和俯仰角指标进行直接比较,见图6.
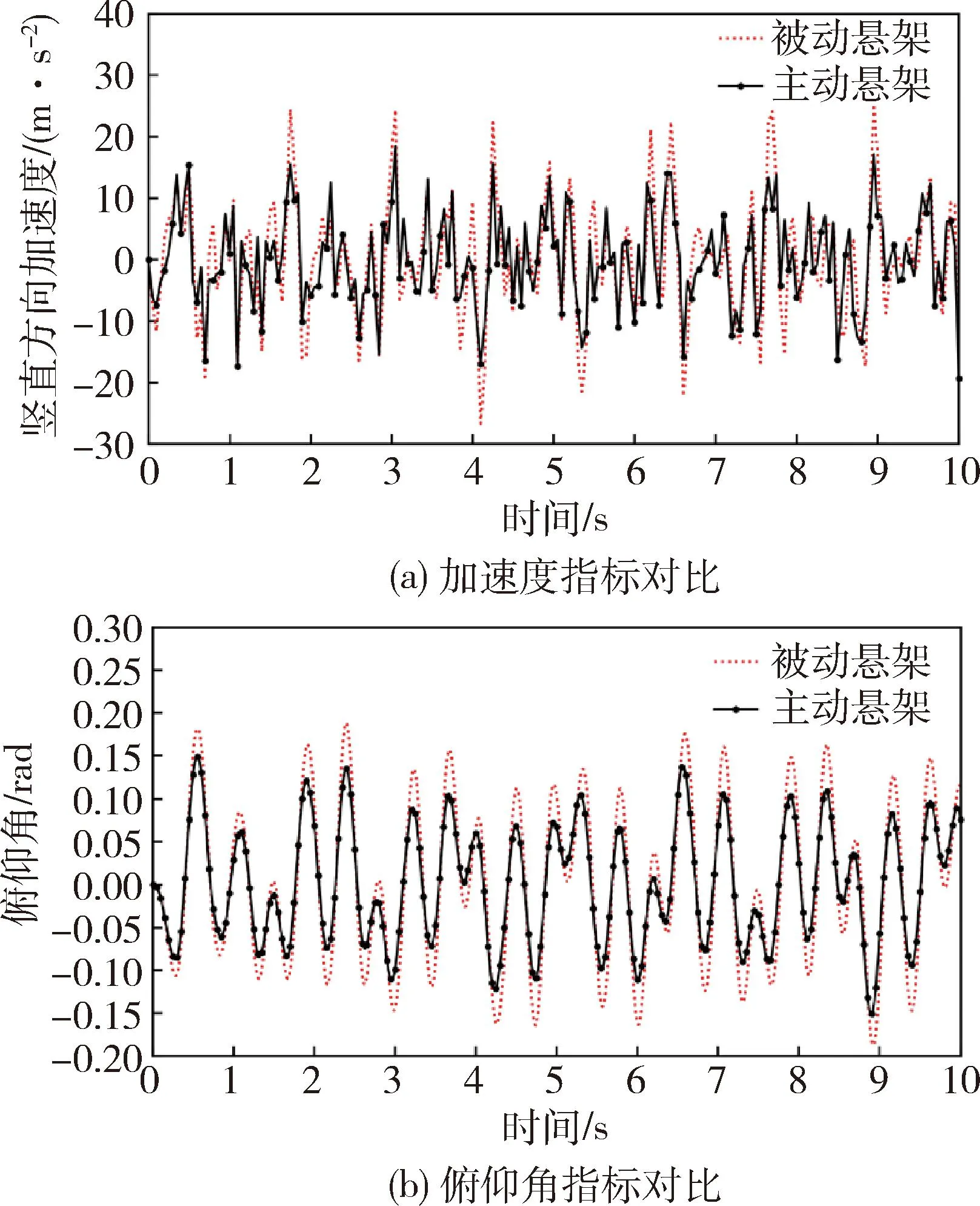
图6 F级路面60 km/h工况下平顺性指标对比
图6所示为履带车在F级路面以60 km/h速度运行工况(最恶劣工况)下竖直方向加速度和俯仰角指标的对比,虚线表示被动悬架,带实心圆的实线表示采用文中控制策略的主动悬架,横坐标为仿真时间.
从图6中可以看出,在加速度和俯仰角图线的每一个峰谷值处,主动悬架对应的指标绝对值均明显低于被动悬架,证明在仿真时间范围内,主动悬架的振动性能稳定地优于被动悬架.从表3和图5中已经得知,主动悬架整体性能优于被动悬架,而图6进一步说明,具体到某工况的运行过程中,悬架的振动幅度得以减小,性能得到提升.
4 结 论
履带式车辆的振动控制是整体性能的重要突破点.文中提出了一种基于协同控制的悬挂控制策略,并完成了全工况下履带车动力学模型及天棚控制器的实现.在不同路面等级和运行速度下,以平顺性为评价指标,对履带车进行了半主动悬挂性能的分析.仿真结果表明,改进的履带车天棚控制模型有效缓解了由路面激励引起的履带车辆的振动,车辆平顺性的加速度和俯仰角指标均有提升效果,最大提升为33.84%.其中,运行速度较快时,平顺性提升效果更加显著.
此外,在多种工况下采用同一种控制参数,其控制效果存在差异,部分工况下仍有提升空间.后续研究可考虑根据不同的路面等级和车辆运行速度,选择不同的控制参数.

