面向不同站间距的无网受流列车运行能量分析

张建敏， 闫 愿， 郝文美

(1.中车唐山机车车辆有限公司产品研发中心，唐山 064000；2.北京理工大学 电动车辆国家工程研究中心，北京 100081)

随着城市交通的不断发展，环境友好的城市轨道交通车辆成为城市综合交通发展战略框架中的重要组成部分.然而，目前使用的架空接触网的供电方式存在着摩擦电火花，景观性较差等诸多弊端.而感应电能传输(Inductive Power Transfer，IPT)技术是将电能以非接触的方式从供电电源传递给用电负载，具有安全、可靠、供电灵活等优点，因此，感应电能传输技术大功率化并应用于城市轨道交通已经成为国内外近几年研究的焦点.

IPT技术应用于城市轨道交通领域时，列车全线无接触网，而由于路权占用及线路适应性问题，无线供电系统无法全线铺设，脱线路段的存在就要求车辆必须自带车载储能装置实现能量供给，车辆停站无线充电实现能量补充，车载储能满足站间能量消耗.在这样的前提下，站间距、车载储能、无线充电功率与充电时间彼此相互影响，因此，基于不同站间距的运行工况明确运行能量是无网受流列车的稳定运行的关键.目前，已经有了诸多学者进行了能量策略的研究，主要可分为3个研究方向：基于实时检测车速、车载电池的荷电状态、驾驶员需求功率和此时汽车的工作模式(牵引或制动)等变量进行能量的控制[1-5]；对燃料电池混合动力汽车进行了研究，其动力源有燃料电池、蓄电池及超级电容，分别提供负载功率中的低频部分、中频段功率及高频部分[6-9]；基于动态规划法[10-13]、模糊控制[14-15]等优化方法，将车辆需求功率和动力电池的能量状态作为参数输入，发电机的输出功率为参数输出，实现了整车的能量分配，有效地提高了整车的燃油经济性，并使动力电池始终保持在高效区域内运行.

文中以100%低地板城轨列车为基础，对无网受流列车运行过程中的能量流动情况进行分析，根据车辆在线行驶段及脱线行驶段的能耗情况，计算得到无线充电功率与储能系统配比及车辆脱线比.并基于不同的站间距进行算例分析，明确不同站间距运行情况下车辆的能量流动、储能容量及充电功率需求.

1 系统结构

无接触网供电城轨车辆动力系统结构如图1所示，直流母线电压通过高频逆变器转换为高频交流电，再通过感应供电的方式传递给副边线圈，提供车辆动力驱动需要的能量并向储能系统充电.

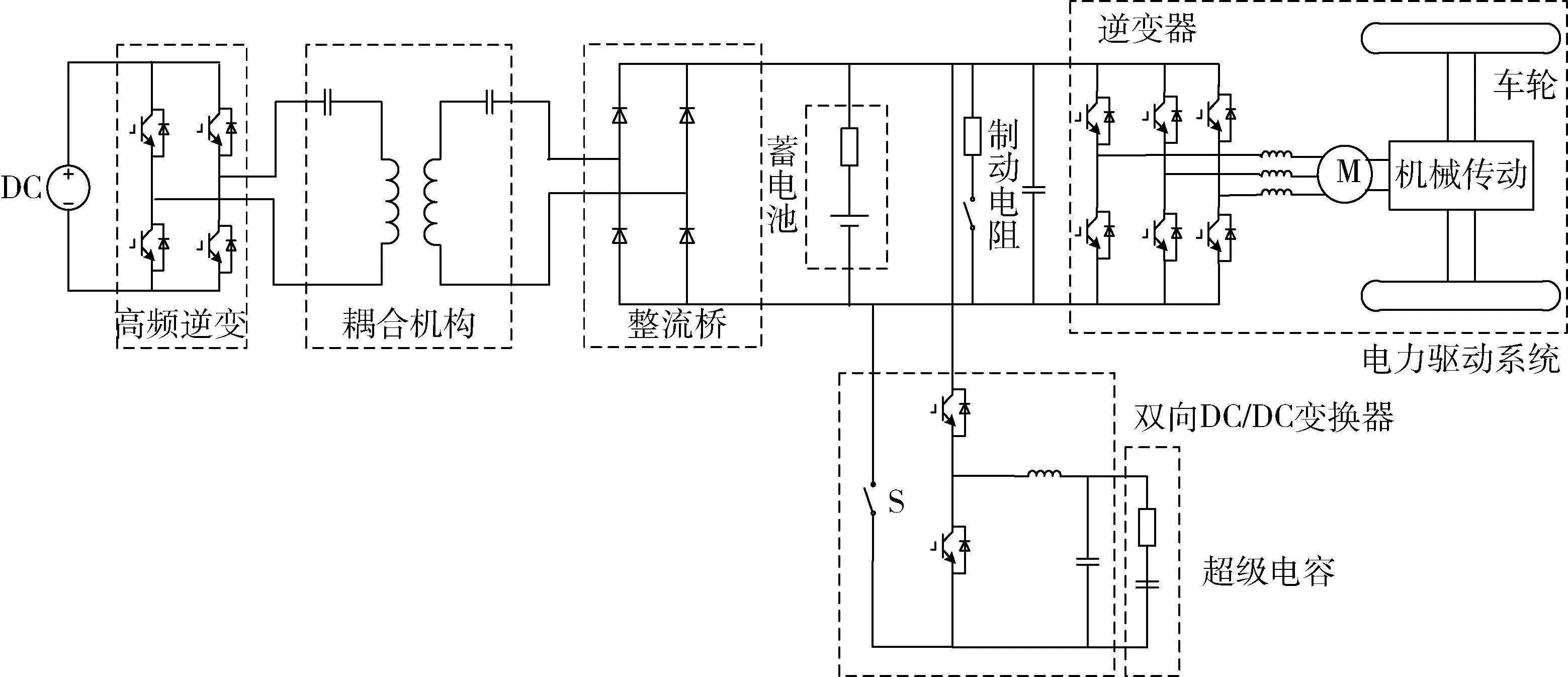
图1 无接触网供电城轨车辆动力系统结构

无接触网供电系统提供的供电功率PW基本保持恒定，稳定向车辆提供能量.车载储能系统需承担峰值功率，吸收制动回馈能量并通过无线充电补充自身能量.因此，无线电能传输及储能系统提供车辆运行过程中所需的全部能耗，以保证车辆的加速、制动、恒速运行、脱网运行及一些弯道、坡道等特殊路况造成的车辆附加能耗.能量管理系统结构其功能如图2所示.

图2 能量管理系统结构及供能

由系统结构可知，无接触网供电城轨车辆能量管理策略的设计原则为：以无网受流供电为主，储能系统为辅，两者峰值功率的叠加要大于车辆最大消耗功率.因此，无网受流功率及储能系统的能量配比须由车辆能耗情况进行综合分析.

2 能量管理

车辆正常运行过程中可以分为3个阶段，牵引启动阶段，以最大行驶速度恒速运行阶段，减速制动阶段.列车牵引制动特性曲线示意如图3所示.

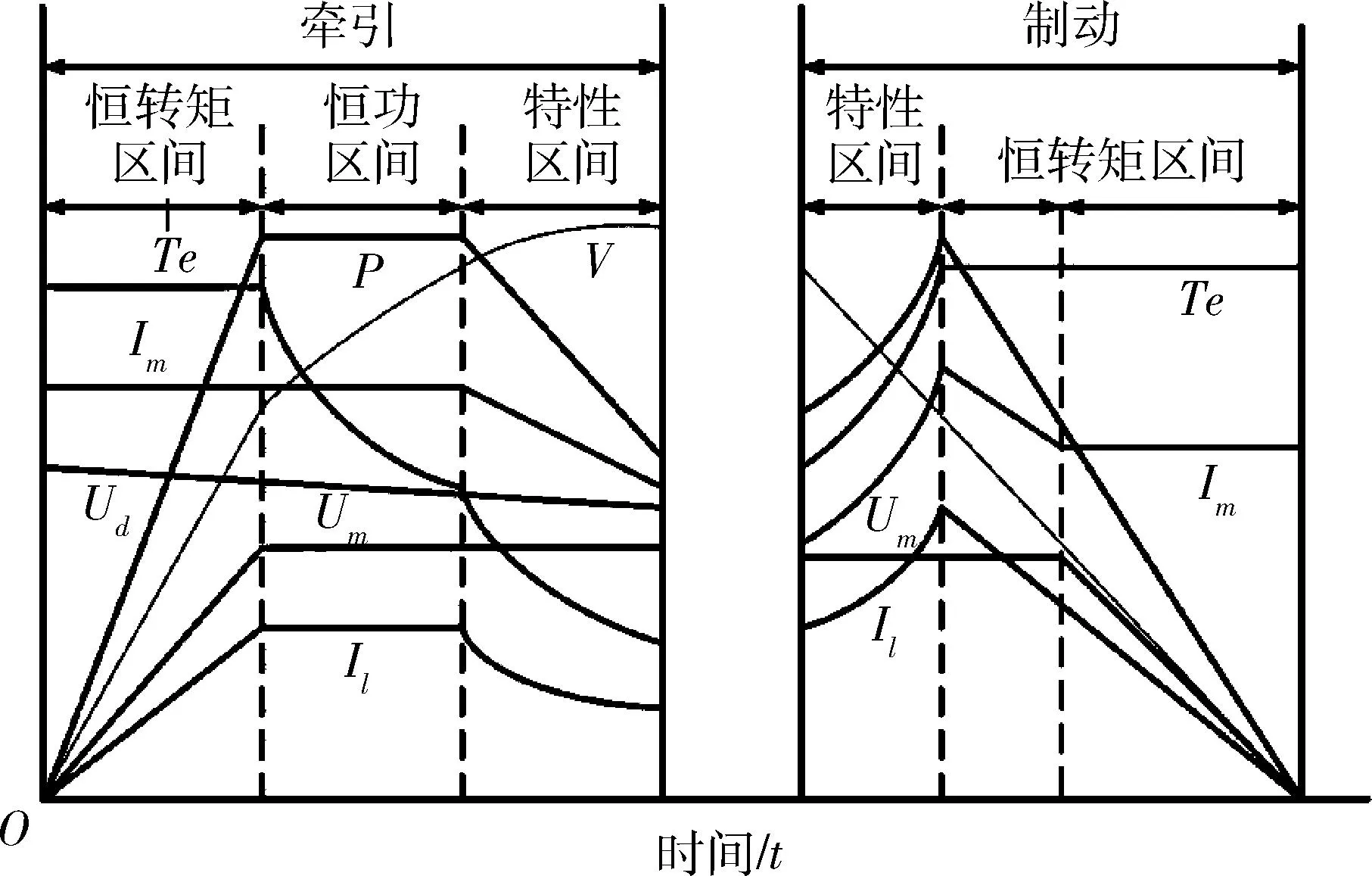
图3 列车牵引制动特性曲线示意

2.1 启动阶段

城市轨道交通车辆牵引启动阶段可分为3部分，分别为恒转矩区、恒功率区和自然特性区.当城轨车辆处于恒转矩区时，列车的转矩即牵引力保持不变，为与列车速度无关的一个常数；处于恒功率区时，输出的牵引功率保持恒定，车辆的牵引力与运行速度成反比，最大牵引功率出现在恒转矩区到恒功率区开始时刻，此后以最大牵引功率维持一段时间，在这个阶段储能系统要求放电功率达到最大；当车辆处于自然特性区域，车辆牵引力与列车运行速度平方的乘积为一常数，启动阶段功率要求较高，需由储能系统补充峰值功率，结构如图4所示.

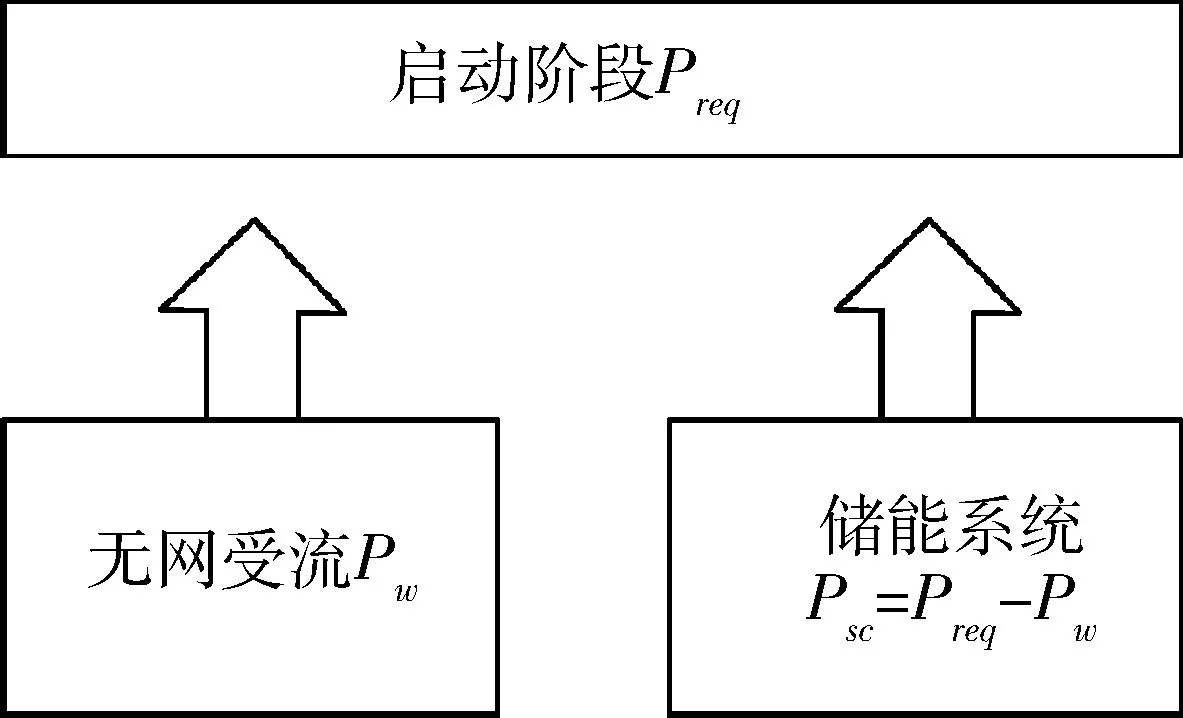
图4 启动阶段能量配比

忽略附加阻力，列车启动过程中所需系统提供的能量为启动阻力耗能、基本阻力耗能、车辆动能增量这3项之和[7]，即

E=EFq+EFj+Ek，

(1)

式中：EFq为启动阻力耗能；EFj为基本阻力耗能；Ek为动能增量.

启动阶段需要储能系统提供能量支持，考虑到转换效率和充沛裕量，储能系统存储的能量要大于车辆牵引运行时总的能量消耗，即Esc>E.

2.2 制动阶段

当列车准备进站停车时，牵引电机进入再生制动状态，回馈能量.列车实际运行时，制动阶段可分为两部分，自然特性区和恒转矩区，自然特性方式制动时，车辆制动力与列车速度平方乘积为一个常数；进入恒转矩制动阶段后，再生制动功率随着车速减小逐渐到零，制动功率最大发生在制动阶段恒转矩刚开始时刻[8].

忽略附加阻力，列车在制动过程中，车辆无需通过无网受流获取电能，将动能转换为电能回馈至储能系统中，储能系统能量饱和后，再生制动将自动切换为电阻制动，将再生到直流电路的能量通过电阻变成热能消耗掉，使直流母线电压保持在允许范围之内，结构如图5所示.

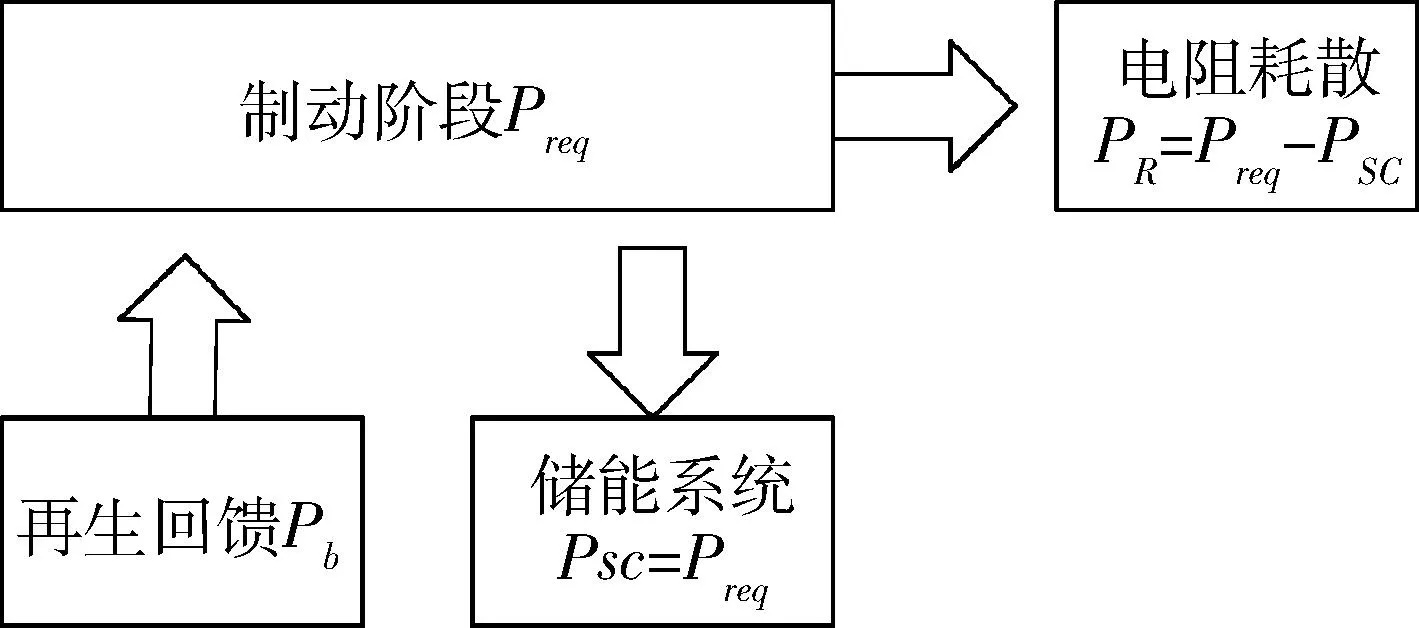
图5 制动阶段能量配比

列车制动过程中回馈能量为动能转化的电能，减去制动过程中的基本阻力消耗，即

E=Ek-EFj，

(2)

式中：EFj为基本阻力耗能；Ek为动能转化为的电能.

为避免电阻上的能量耗散，提高系统效率，储能系统应尽可能吸收全部的制动回馈能量，即Esc>E.

2.3 恒速阶段

由于建设条件、道路情况等限制，必然存在有些路段无法铺设非接触电能传输装置，因此，车辆恒速状态可分为在线行驶及脱线行驶.车辆在线行驶时，无网受流需提供车辆牵引能耗，并向储能系统充电，以满足脱线行驶需要；脱线行驶时，储能系统需提供车辆运行所需的全部能耗，结构如图6所示.

图6 恒速阶段能量配比

车辆正常运行过程中存在的阻力分为基本阻力和附加阻力，基本阻力是车辆在任何情况下都存在的阻力，主要包括轴承阻力、滚动阻力、滑动阻力、冲击振动阻力和空气阻力这5个部分.而附加阻力只在运行特殊情况才产生.基本阻力公式为

Fj=a+bv+cv2，

(3)

式中：Fj为辆运行的基本阻力，kN；a，b，c为阻力系数，其中，根据工程经验取a=2.59，b=0.092，c=0.001；v为车辆的运行速度，km/h.

车辆进入恒速运行过程后，其速度基本保持不变，牵引力主要是克服此时列车运行的基本阻力.当车辆以平均车速va行驶下每公里平均能耗Qa为

(4)

此时，无网受流提供能量为

(5)

在线行驶时储能系统每公里可获得

(6)

车辆在线以平均速度行驶时，储能系统充得的可用能量为

E=L*QCS.

(7)

式中：L为在线行驶距离.

因此，车辆脱线后可行驶的距离为

(8)

可得无网受流功率Pw与车辆在线行驶距离L与脱线行驶距离D的关系如图7所示.

图7 无网受流功率Pw，在线距离L与脱线距离D的三维关系图

由图像可以看出，随着脱线行驶线路长度的增加，对无网受流功率的要求也会相应变大，因此，可以根据线路情况选择合适的功率，也可以根据功率对可行驶的线路条件及车载储能系统的容量进行约束.

假设储能系统的容量为Esc，由于电压及放电深度的限制，车辆理论最大脱线行驶里程Dmax为

(9)

式中：λ为储能系统放电深度.

提升自身的知识技能和个人素养，也是增加婚恋筹码、规避单身的重要途径之一。现阶段精准扶贫过程中，劳动部门举办了多次专门针对贫困农村青年的职业技能培训和就业辅导，农村青年应抓住有利机遇，积极学习，掌握一技之长，提高致富能力，摆脱经济上的贫困，增强在婚姻市场上的竞争力，从而降低单身的几率。

3 算例分析

无接触网供电城轨列车采用100%低地板车为试验车型，车辆基本参数及运行参数如表1所示.

表1 无接触网供电城轨车辆基本运行参数

表2 不同站间距耗能

仿真得到列车牵引特性结果如图8～10所示.

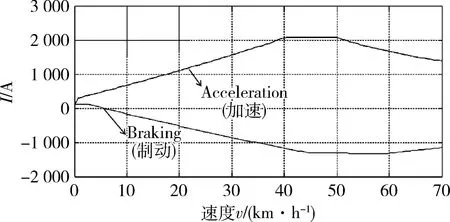
图8 接触网电流曲线

图9和10的仿真工况：AW2车辆数量为4；传动比为6.29；轮径(半磨耗)为0.57 m.

图9 列车牵引启动阶段牵动或阻力与加速度的仿真结果

3.1 车辆运行耗能计算

针对列车图像及数据进行站间2 km运行耗能计算：

(1)启动阶段

1)恒转矩(0～40 km/h)

2)恒功率(40～50 km/h)

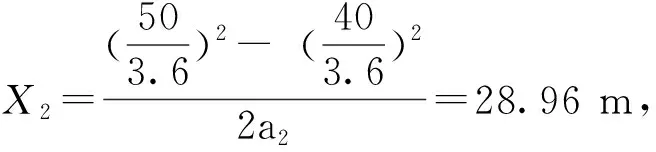
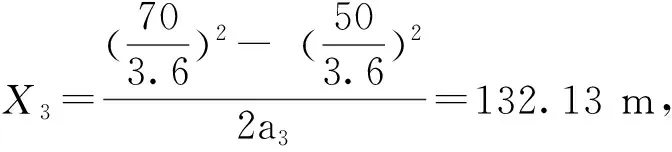
综上，启动阶段运行时间为T1=18.1 s，运行距离为S1=X1+X2+X3=205 m，耗能为W启=W1+W2+W3=5.7 kWh.

(2)制动阶段

此时车辆动能W动= mv2=0.5×76.7×103×19.442=14 474.09 kJ=4.02 kWh.

1)恒功率(70-45 km/h)

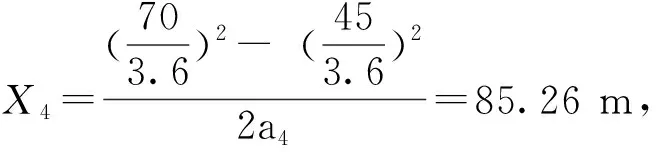
图10 列车制动阶段电制动力与电制动减速度的仿真结果

2)恒转矩(45-0 km/h)

由图10减速度基本不变，取值a5=1.05 m/s2，则恒功率减速阶段时间为t5=45/3.6/1.05=11.9 s，行驶距离为X5=1/2×1.05×11.92=74.35 m，由图8可知此阶段电流基本呈线性减少，取均值为650 A，电压选择825 V，由此可得再生制动能量为W5=650×825×11.9=6 381.375 kJ=1.77 kWh.

综上，制动阶段运行时间为T2=17.24 s，运行距离为S2=X4+X5=159.6 m，再生制动能量为W制=W4+W5=3.36 kWh.此阶段辅助耗能0.34 kWh.

(3)匀速阶段

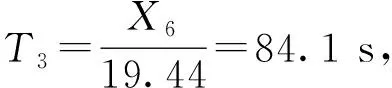
综上，整个2 km的站间运行区间内，运行时间T=18.1+17.24+84.1=119.44 s，辅助耗能为W辅=72×119.44/3 600=2.4 kWh，所以最后总能耗为W=5.7+3.95+2.4=12.05 kWh，再生制动能量为3.36 kWh，总的耗能为8.69 kWh.因此，根据不同的站间距可以得到不同的站间距下的能耗分析如下.

上表所示为正常运行状况之下的能耗计算数据，若按照惰性工况，启动加速至额定速度后，取消牵引与制动，让列车依靠惯性且仅在阻力作用下运行，能耗会更少，可是惰性点比较难掌控.

对于锂电池，若采用常规充电方式，将电池充满需要7到8 个小时，车辆进出始发站的间隔至多一小时，不可能停留这么长时间；而快速充电在充电桩上，采用2 C到3 C的充电电流可以在半小时之内将电池充进80%的电量，但是大电流充电会在电池内部产生大量热量，对电池有一定损伤[2].所以采用锂电池与超级电容一起供能，在终点站给锂电池充电的方式不现实，锂电池只能做备分使用，比如某几站的站间距大于平均站间距时或某一站的充电桩发生故障时使用，而站间全部采用超级电容充电.

3.2 超级电容容量配置与计算

(1)超级电容基本参数

超级电容器组是采用美国Maxwell公司生产的BMOD0063P125B04/B08模组，单体为2.7 V/3000 F.该模组集成度较高，模组自带散热系统及通讯系统，对于车辆供电系统应用来讲比较合适.基本参数见表3.

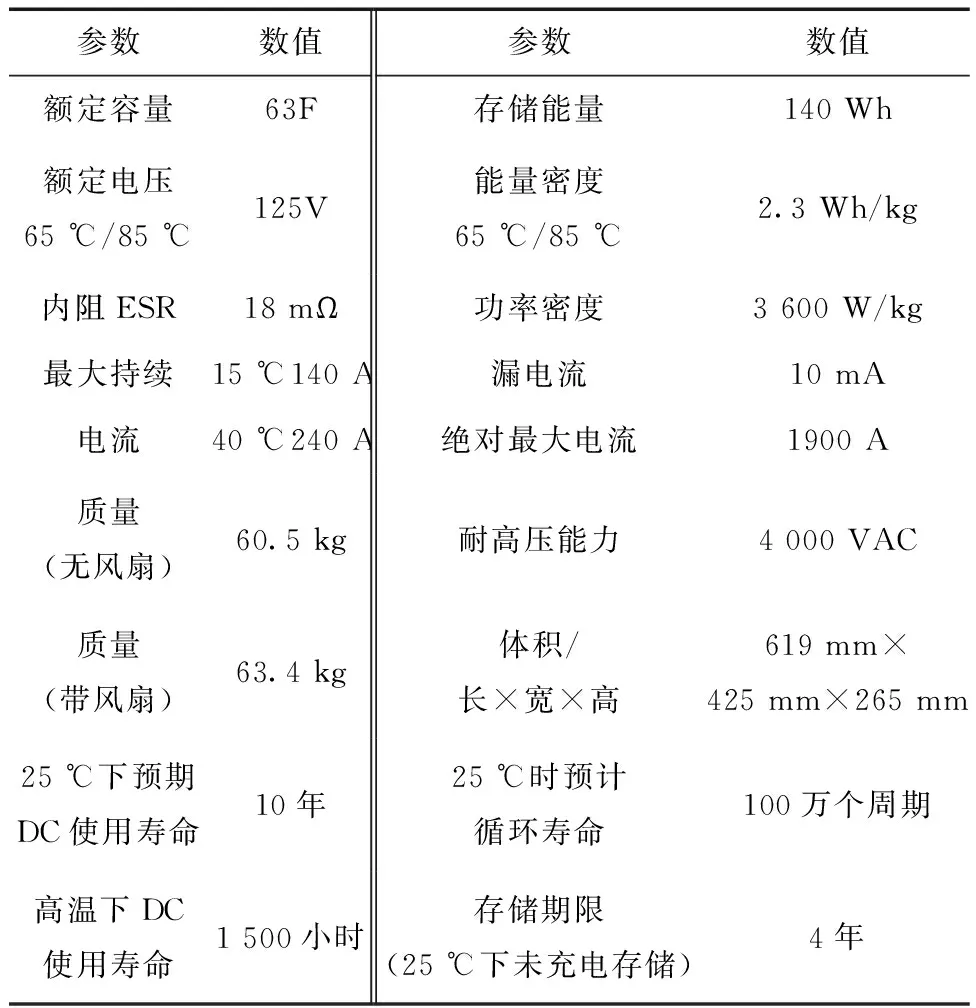
表3 超级电容器模组基本参数

根据车辆500～900 V的电压要求，取8个125 V/63 F超级电容器模组，通过串联的方式组成的超级电容器组，电容储能原系统参数见表4.

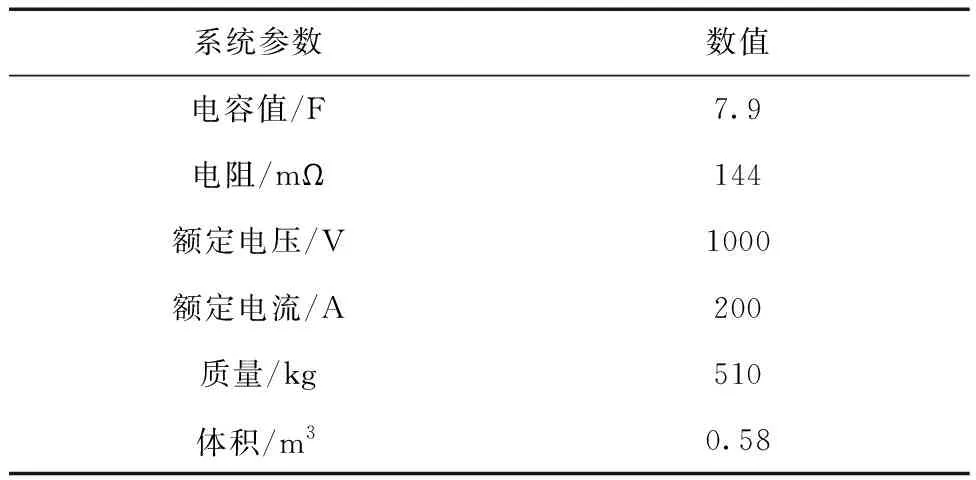
表4 超级电容储能系统参数

(2)超级电容容量配置

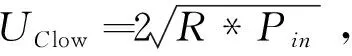
由超级电容组参数可知，此超级电容系统的电压下限制为Wlow=31.5×36×200/3.6×106=0.063 kWh，占总存储量的6.3%.因此，超级电容可释放自身存储量90%左右的能量.

由于所给车辆逆变器所能承受的电压范围为500～900 V，而改变车辆牵引变流器工程较大，改变了无线充电适配于现有列车的初衷，所以，保持直流侧电压波动范围在500～900 V为合理的方案.由超级电容的容量WC=1/2CU2可知，超级电容的电压被限制，则所提供的能量及配置也将受到限制.

考虑额定电压1 000 V的情况，超级电容的电压由900 V降至500 V，容量应对应从81%降至下限值25%，中间释放的容量对应为累计牵引能量(不包含再生能量)，则可计算出对应的总容量.可总结能量流如图11所示.

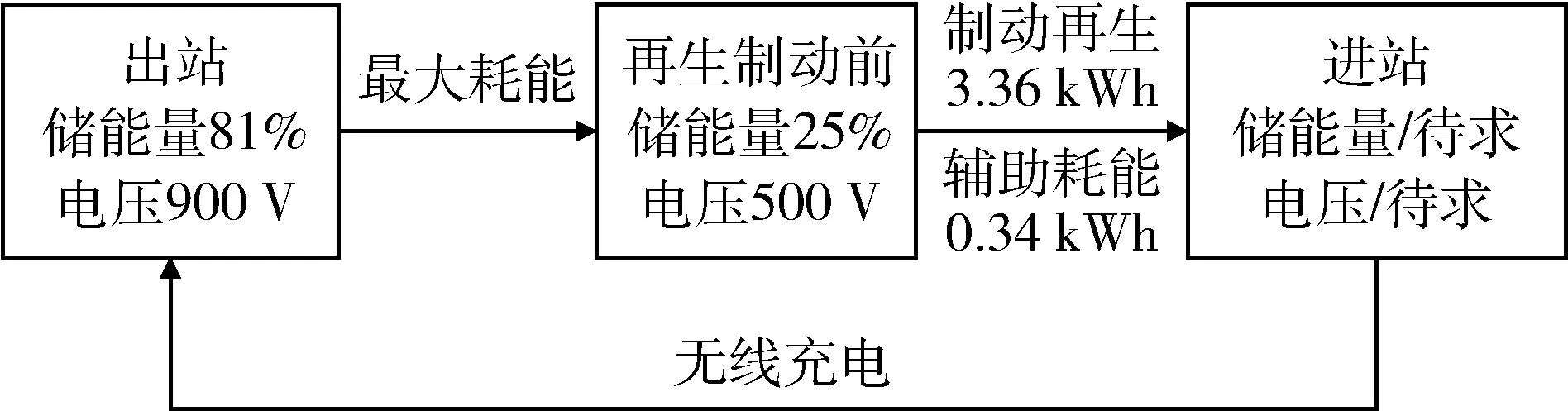
图11 超级电容充放电流程

根据文中表2的不同站间距能耗计算及超级电容器模组的数据，对超级电容模组的输出要求需达到电压>900 V，电流>2 100 A，得到超级电容的容量要求如表5所示.

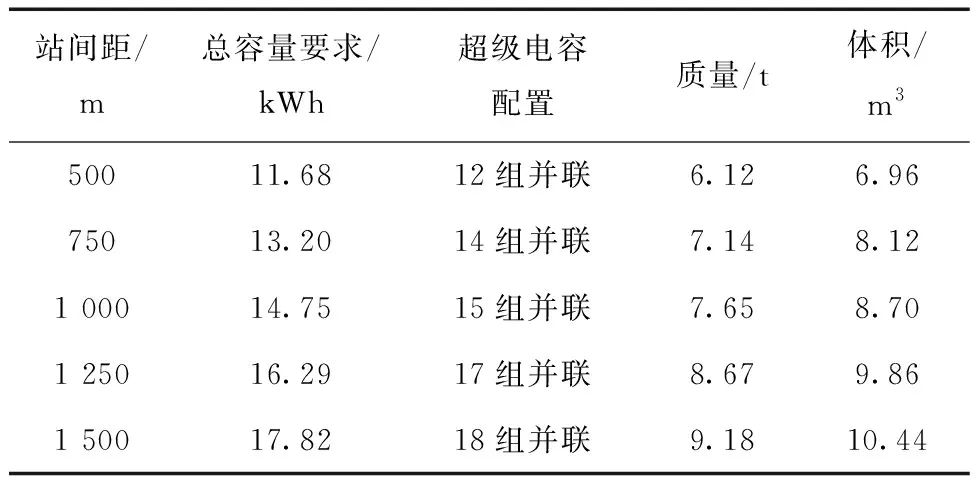
表5 超级电容容量配置

根据上表所得的不同站间距所得的超级电容器的尺寸、重量数据，选取1 200 m为最大站间距比较合理，选用8×16串并结构的超级电容模块组合，理论额定电压1 000 V，额定电流可达到3 200 A.对应超级电容模组的重量为8.16吨，总体体积约为9.3立方米.

3.3 无线充电功率计算

综合前文的分析，根据不同的充电时长与不同的站间距需要，得到表6充电功率，均以90%做为充电效率.

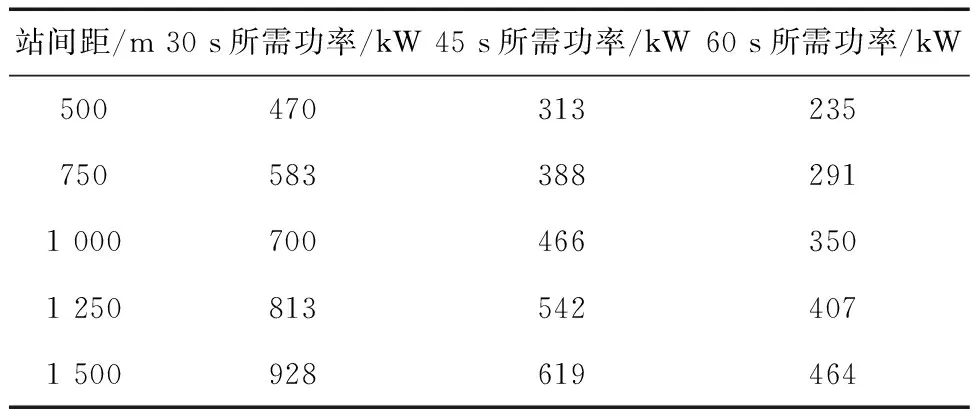
表6 充电功率计算

此表格中，①充电功率只以耗能进行计算，未考虑超级电容充电时电压变化带来的充电功率的变化.以恒流充电计算，电压波动从500～900 V的情况，无线充电系统设计最大充电功率应比上述计算功率高约30%.②此计算仅考虑无坡道、弯道的理想状态计算，这些因素也会影响最终功率计算，使得能耗增加，进而要求充电功率进一步加大.③目前列车计算中，未计算超级电容及无线充电功率拾取侧设备造成的列车质量的增加，加上这部分后，列车质量会增加10吨左右，损耗也会成比例增加10%以上.综合考虑，无线充电系统设计功率应比表格中的计算功率高约50%.参考超级电容设计数据，选用1 200 m为最大站间距，理想站间充电能量为5.93 kWh，对应45秒充电时间(仿真实例为610/14=44秒)，按充电效率90%计，充电功率为527 kW，考虑实际应用功率高50%的情况，静态充电功率应选800 kW.

4 结 论

文中针对无网受流列车实际应用过程中的运行能耗分析及各环节能量配置问题，首先基于无接触网供电城轨车辆动力系统结构，明确了能量管理系统的整体结构及供能方向.接着结合列车牵引制动特性曲线，分析了启动阶段、制动阶段及恒速阶段能量配比及运行脱线比.最后以100%低地板车作为分析对象，结合车辆实际牵引制动仿真曲线对车辆各阶段运行能耗进行计算，在不同站间距能耗的基础上，结合超级电容模块参数及放电特性，提出1 200 m的最大站间距要求，并基于此，选择了8×16串并结构的超级电容模块组合及800 kW的无线充电功率要求.文中提出的容量匹配方法及储能设计流程，为无网受流列车的实际应用及站间规划提供良好基础及理论指导.