不确定环境下多无人机任务分配

徐庆征，马依笑，王 娜

（国防科技大学信息通信学院，湖北武汉，430015）

0 引言

无人机具有成本低、无人员伤亡、操作方便、运用灵活、性能可靠等优点。近年来，无人机技术发展迅速，引起世界各国的高度关注[1]，在军事和民用领域获得广泛应用，包括目标监视、遥感、多目标跟踪等。随着任务复杂度的大幅提升，单一无人机并不能轻易地完成多项任务。因此，无人机集群之间的协同配合显得尤为重要[2]。

无人机集群协同的典型样式包括碰撞规避、任务分配、路径规划以及编队重构等。其中，任务分配是指在满足一定任务需求和无人机性能的前提下，将多项子任务分配给各架无人机，协同完成一项复杂任务[3]。针对多无人机任务分配问题，人们提出了多种方法，主要包括4种类型：集中式算法、分布式算法、群智能算法以及基于多融合的算法[4]。本文采用的差分进化（Differential Evolution，DE）算法属于群智能算法的范畴。

随着战场环境干扰因素的不断增加，实际的任务分配问题往往面临着部分信息不确定的困境。在这种时代背景下，对不确定环境下多无人机任务分配问题的研究逐渐成为当前热点[5]。针对单无人机任务分配问题和多无人机任务分配问题，文献[6]分别提出了基于一致性拍卖算法和基于一致性包算法，这2 种算法都不受态势感知的不一致性支配，能够分别产生无冲突的分配方案。随后，该方法又被扩展至解决不确定环境下异构无人机的任务分配问题[7]。2004 年，研究人员提出了1种基于嵌入式滤波器的鲁棒任务分配算法，实现了无人机在不确定动态环境下的任务分配[8]。文献[9]将区间直觉模糊集引入空战多目标威胁评估中，解决了传统方法在测量误差及空战环境方面造成的信息不确定性问题。2019年，针对多无人机在不确定环境下，面向压制敌防空系统约束的任务分配问题，研究人员提出1 种基于区间直觉模糊决策的多无人机任务分配方法[10]，借助逼近理想解排序法，作者考虑曼哈顿距离和犹豫度，求解每一个区间直觉模糊数对于最大区间直觉模糊数的相近度。

在复杂战场环境下，红方能够较容易地获知各架无人机的地理坐标，但是拟攻击的蓝方目标的地理坐标可能并不精确，或者在飞行过程中遇到了不可抗力，这都将导致无人机与攻击目标之间的距离是1 个模糊数。本文将其抽象为1 个区间数，即d=[dL,dU]，其中，dL,dU∈ℝ，dL＜dU。

本文的贡献主要包括以下3点：1）构建了不确定环境下多无人机任务分配的数学模型；2）提出了3种多变异策略的差分进化算法，以便最大限度地发挥各种变异策略的技术优势；3）重新设计了差分进化算法的编码方式和进化算子，以适合不确定环境下多无人机任务分配问题。特别是基于区间数排序方法，依照可能度来计算候选解被选中进入下一代的概率。

1 不确定环境下多无人机任务分配的数学模型

假定存在n架无人机以及n项任务需要执行，每项任务恰好需要1 架无人机。简而言之，多无人机任务分配问题就是确定哪架无人机去执行哪项任务，使得完成这些任务的总成本最低或总收益最高。本文中，总成本采用各架无人机与相应任务之间的距离之和来加以描述。

在该数学模型中，目标函数就是各架无人机与相应任务之间的距离之和，如下：

在该数学模型中，约束条件如下：

式（2）表示每架飞机只需要执行1 项任务；式（3）表示每项任务只需要1架飞机加以完成。

2 求解方法

2.1 差分进化算法

1995 年，美国学者Storn 和Price 首次提出了差分进化算法。该方法采用模拟生物进化的机制，通过种群内个体差异度生成变异个体，然后进行交叉、选择操作，实现种群的迭代进化。该算法具有原理简单、效率高、参数少、适用性强等特征，非常适合于一些常规数学规划方法不能或难以求解的复杂优化问题，其已在许多科学和工程优化等领域得到广泛应用。

标准差分进化算法的进化过程如下所述。

步骤1 种群初始化。

根据式（4），产生Np个向量粒子，构成初始种群。

式（4）中：rand表示[0，1]内均匀分布的随机数；xi_min和xi_max分别表示每一个向量粒子的每一维分量的上界和下界；i=1,2,…,Np；j=1,2,…,Nd；Np表示种群规模，即向量个数；Nd表示向量粒子的维度。

步骤2 变异操作。

差分变异操作通常是在1个基向量的基础上加载1 个缩放后的差分向量，得到变异向量。常用的变异策略如下：

式（5）中：F是变异缩放因子；vi是新产生的变异向量粒子；xi1、xi2和xi3是随机选择的互不相等的3个向量粒子。

步骤3 交叉（重组）操作。

为了维持变异向量的多样性，引入交叉操作，得到试验向量ui。交叉模式包括二项式交叉模式和指数交叉模式，本文使用的是二项式交叉模式：

式（6）中：CR是交叉概率；jr是随机选择的1 个维度，以确保至少有1个维度被更新。

步骤4 选择操作。

差分进化算法是基于贪婪原则来选择下一代向量个体。对于最小化问题，适应度值越小，表示个体越优秀，如下所示：

步骤5 终止条件判别。

如果算法取得理论最优值或者达到最大函数评价次数MaxNFC，则该种群进化过程结束；否则，重复步骤2～4。

2.2 差分进化算法求解多无人机任务分配问题

在标准差分进化算法中，各个进化算子操作能够直接应用于连续函数优化问题。针对多无人机任务分配问题的特殊性，须要重新设计编码方式、进化算子等。

2.2.1 编码方式

文中，向量个体采用整数编码机制。长度为无人机（或拟执行任务）的数量n，每个基因都为整数值，代表着所在位置的无人机拟执行的任务序号。

假设有5 架无人机和5 项任务，某候选解向量的编码如图1所示。该向量表示，第1架无人机执行第3项任务，第2 架无人机执行第5 项任务，第3 架无人机执行第1 项任务，第4 架无人机执行第4 项任务，第5架无人机执行第2项任务。

图1 向量个体编码示例Fig.1 Example of vector coding

2.2.2 种群初始化

按照2.2.1 节所述的编码方式，随机产生Np个向量个体，共同构成初始种群。

2.2.3 变异操作

求解多无人机任务分配问题时，仍然可以采用如式（5）所示的DE/rand/1 变异策略。须要注意的是，由于变异缩放因子F通常是1个小数，计算得到的变异向量vi不再是1个可行候选解。

本文提出1 种变异操作的修补策略，以便快速获得1个可行的候选解。首先，按照式（5）计算得到1个临时的变异向量v′i；然后，将计算得到的变异向量v′i的各个维度，按照数值由小到大进行排序。此时，就得到1 个可行的变异向量vi。例如，假设随机选取了3 个 向 量xi1=(3 5 1 4 2 )、xi2=(1 5 4 2 3) 和xi3=(4 1 2 3 5) ，变异缩放因子F=0.5。根据本节提出的修补策略，首先，按照式（5）直接计算得到v′i=(5 1 0.5 4 4.5) ；然后，对各个维度进行排序处理，就得到1个可行的变异向量vi=(5 2 1 3 4 )。

2.2.4 交叉操作

本文的差分进化算法仍然采用二项式交叉模式。须要注意的是，此时的交叉操作不再以变异向量的各个维度为操作对象，而是以各个变异向量为操作对象，如式（8）所示：

显然，这种处理方式能够有效避免算法产生不可行解，提高算法计算效率。

2.2.5 越界处理

按照前述变异和交叉操作，新产生的试验向量一定符合编码规则，是1个可行解。因此，无需额外的越界处理过程。

2.2.6 选择操作

本文的差分进化算法仍然基于贪婪原则选择下一代向量个体，如式（7）所示，无须任何改动处理。

2.3 区间数的排序方法

在复杂战场环境下，无人机与攻击目标之间的距离具有不确定性，本文将其抽象为1 个区间数。区间数是1 种描述不确定性信息的有力工具，它最早由Moore 提出，目前已广泛应用于多属性的不确定性决策、模糊控制等领域[11-12]。在应用区间数描述不确定性信息的决策过程中，除了要解决对区间数进行合成（加、减、乘和除法等）的问题，还要解决区间数排序的问题。

现有的区间数排序方法大致可以分为如下几类：确定性排序方法、基于序关系的区间数排序方法、基于粗糙集的区间数排序方法、基于集对分析的区间数排序方法、基于向量相似度的区间数排序方法、基于距离测度的区间数排序方法、基于概率分布的区间数排序方法、基于优势度的区间数排序方法、基于可能度的区间数排序方法等[13-14]。其中，基于可能度的区间数排序方法是目前应用最为广泛的1 种排序方法。其基本思想是，通过定义1种反映1个区间数大于另1个区间数程度的量，并以该度量为基础导出区间数之间的排序。

设区间数a=[aL,aU] 和b=[bL,bU] ，记p()a≥b为a≥b的可能度。可能度能够衡量2 个区间数之间的大小关系，它的取值一般在0～1之间，其数值大小根据不同的可能度定义公式来确定。

区间数a和b服从均匀分布，而且它们的取值情况是相互独立的，因此，计算可能度p(a≥b)就等价于计算u＞v的概率，其中，u和v分别表示区间a=[aL,aU]和b=[bL,bU]内的1个随机取值[15]。计算结果如下：

式（9）中，L(a)=aU-aL，L(b) =bU-bL。

2.4 差分进化算法求解不确定环境下多无人机任务分配问题

在不确定环境下多无人机任务分配问题中，将无人机与攻击目标之间的距离抽象为1 个区间数，会造成2 个新问题，须要研究解决：一是适应度（无人机与执行任务之间的距离）的计算；二是选择操作。

本文将适应度区分为适应度下界和适应度上界，分别加以计算。当计算适应度下界时，基于各个区间数的下界，代入目标函数；相应地，当计算适应度上界时，基于各个区间数的上界，代入目标函数。最终，适应度的输出结果同时包括这2个计算结果。

在选择操作中，算法把2 个区间数排序的可能度作为选择候选解的依据。例如，p()a≥b=0.6，那么，本文的差分进化算法将以60%的概率选择区间数b所对应的解xb，同时以40%的概率选择区间数a所对应的解xa。注意，可能度的计算过程已在2.3 节详细叙述，此处不再赘述。

3 基于多变异策略的差分进化算法

3.1 改进动机

差分进化算法的核心操作为变异操作。为了提高寻优的成功率，研究人员提出了多种变异策略。主要包括4种变异策略。

1）DE/rand/1变异策略：

2）DE/rand/2变异策略：

3）DE/best/1变异策略：

4）DE/best/2变异策略：

文献[17]分析了几个经典变异策略的优化特性，并指出：如果采用“rand”形式的变异基向量，算法具有较大的寻优范围，全局收敛性好，但是收敛时间偏长，因而对解决多峰问题表现比较好；采用“best”形式的变异基向量，算法收敛速度比较快，但易陷入局部最优，因而对解决单峰问题表现比较好。

综上，各种变异策略的内在特点和适用场合不尽相同，故很难找到1 种变异策略能够完美地解决所有的问题。为了最大限度地发挥各种变异策略的技术优势，本文尝试将4种经典变异策略进行多种组合，提出了3种多变异策略的差分进化算法。

3.2 3种多变异策略的差分进化算法

3.2.1 多变异策略的差分进化算法1

在多变异策略的差分进化算法1（Differential Evolution with Multi-Mutation strategies 1，DE-MM1）中，4 种变异策略能够以均等的机会被选中。因此，DE-MM1中变异向量个体的产生如下：

3.2.2 多变异策略的差分进化算法2

1个好的搜索算法应该在初始阶段尽量保持种群多样性，注重算法的探索能力，进行全局搜索；而在算法搜索后期偏重算法开发能力，进行局部搜索，以提高算法的收敛速率和精度。

因此，在多变异策略的差分进化算法2（Differential Evolution with Multi-Mutation Strategies 2，DEMM2）中，在算法搜索前期，更多地采用DE/rand/1 变异策略和DE/rand/2变异策略（以均等的机会使用这2种变异策略）；在算法搜索后期，更多地采用DE/best/1变异策略和DE/best/2变异策略（以均等的机会使用这2种变异策略）。

DE-MM2 中变异向量产生的流程图如图2 所示。其中，G表示当前进化代数，MaxG表示最大允许进化代数。

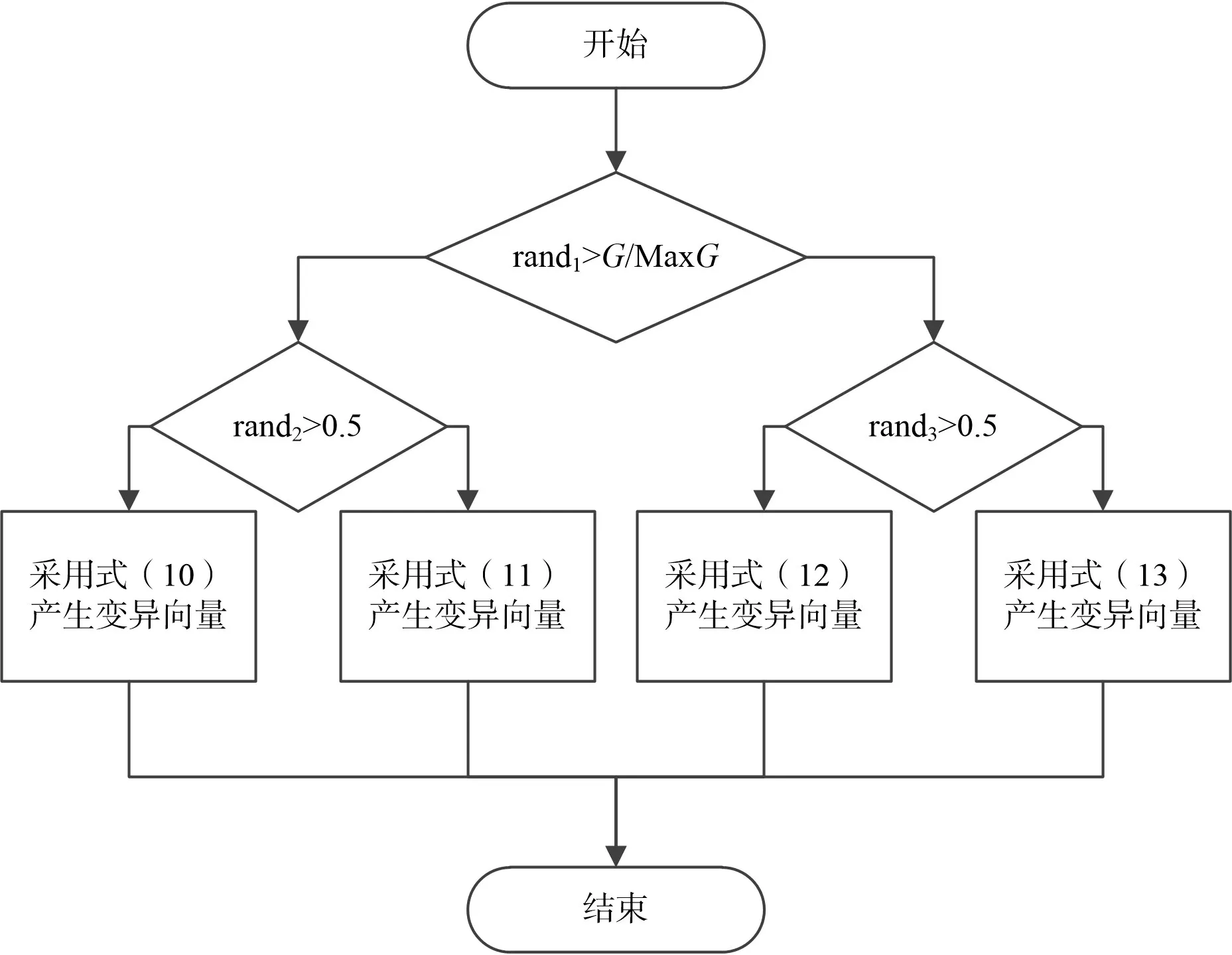
图2 DE-MM2中产生变异向量的流程图Fig.2 Flowchart of mutation vector generation in DE-MM2

3.2.3 多变异策略的差分进化算法3

在多变异策略的差分进化算法3（Differential Evolution with Multi-Mutation Strategies 3，DE-MM3）中，将当前种群划分为2部分：优秀个体子种群和劣等个体子种群。对于前者，改进的差分进化算法更倾向于开发能力，执行局部搜索（以均等的机会使用DE/best/1 变异策略和DE/best/2 变异策略）；对于后者，改进的差分进化算法更倾向于探索能力，执行全局搜索（以均等的机会使用DE/rand/1 变异策略和DE/rand/2变异策略）。DE-MM3中变异向量产生的流程图如图3所示。

图3 DE-MM3中产生变异向量的流程图Fig.3 Flowchart of mutation vector generation in DE-MM3

在DE-MM2中，各个向量个体执行全局搜索或局部搜索的概率是相等的，它只与当前进化代数相关。相反，在DE-MM3 中，各个向量个体执行全局搜索或局部搜索的概率是不相等的，它与其适应度排序相关联。个体的适应度越小，个体性能越优，就以更大的概率执行局部搜索。需要注意的是，此处的选择概率仍然取决于当前进化代数和最大允许进化代数。

4 实验结果与讨论

4.1 求解函数优化问题

4.1.1 实验建立

4.1.1.1 测试集

为了验证新算法的性能，将这3 种多变异策略的差分进化算法应用于CEC2013 的标准测试集[18]。该测试集包括28 个测试函数。其中，f1～f5是单模函数，f6～f20是多模函数，f21～f28是复合函数。

4.1.1.2 实验设置

对于每个问题和维度，每种算法独立运行51 次，以便尽可能地降低算法随机性对算法性能的影响。算法每次独立执行104×n次的函数评估次数。其中，n表示测试函数的维度。

4.1.1.3 算法参数

种群规模Np=50。根据文献[19]的研究成果，使用变异缩放因子F=0.5、交叉概率CR=0.9。

4.1.1.4 终止条件

根据CEC2013 测试协议，本文算法应用了2 种终止条件：1）最大函数评估次数（MaxNFE）达到104×n次；2）算法获得的最优解与全局最优值之间差异值，称为目标函数差值（FEV），小于或等于10-8。

4.1.2 实验结果与讨论

新算法性能可以采取当算法终止运行时所获得的FEV值的最佳值、最差值、平均值、中位数以及均方差等加以评估。表1 展示了3 种算法求解测试函数(D=10 )的性能，包括FEV值的平均值和均方差。

表1 3种算法求解测试函数(D=10 )的性能比较Tab.1 Performance comparison of three algorithms on test functions(D=10)

续表

本文采用统计测试的方法来分析实验结果，以便获得科学、可靠的统计结论。为了获得DE-MM1与另2 种改进差分进化算法之间的统计显著性，本文应用了Friedman检验和Wilcoxon秩和检验，其中显著性水平α=0.05。

表1中：符号“+”表示对比算法的性能要优于DEMM1；符号“ - ”表示对比算法的性能要劣于DEMM1；符号“≈”表示对比算法与DE-MM1之间性能差异不具有统计学意义。

如表1 所示，与DE-MM1 相比较，DE-MM2 在13个测试函数上表现更优秀，只在2 个测试函数上表现更差，在其余13个函数上，2种算法的性能差异不具有统计学意义；DE-MM3 在12 个测试函数上表现更优秀，在8 个测试函数上表现更差，在其余8 个函数上2种算法的性能差异不具有统计学意义。

此外，3种差分进化算法的Friedman检验结果，如表2所示。根据该检验结果可知，DE-MM2排名第一，DE-MM3次之，DE-MM1性能最差。

表2 3种差分进化算法的Friedman检验结果Tab.2 Friedman test results of three differential evolution algorithms

如上所述，3种差分进化算法全部采用了4种变异策略。但是，后2 种差分进化算法根据这些变异策略的技术特点，将其应用在种群进化的不同阶段。具体地，在进化初期，算法需加强全局探索能力，因此，适宜采用rand 型变异策略，而在进化后期，算法更偏重局部开发能力，适宜采用best 型变异策略。实验结果验证了上述改进思路的有效性。

4.2 求解不确定环境下多无人机任务分配问题

4.2.1 实验建立

假设作战区域内共有10 架无人机（地理坐标已知）、10 个任务目标（通过技术手段，能够初步估算出地理坐标）。为描述方便，我们将这些无人机与任务目标分别编为1～10号。无人机的坐标如表3所示，任务目标点的坐标如表4所示。

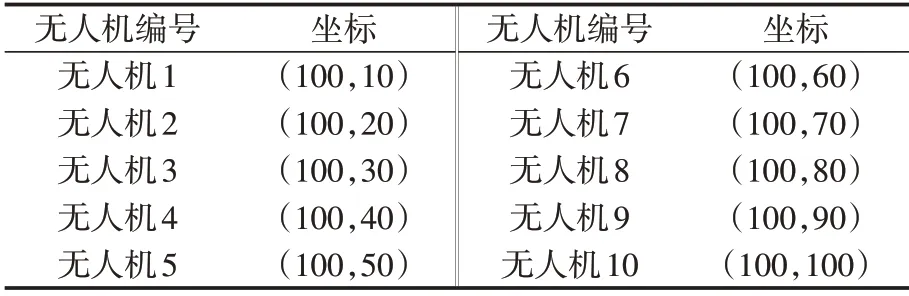
表3 无人机的坐标Tab.3 Coordinates of multi-UAV

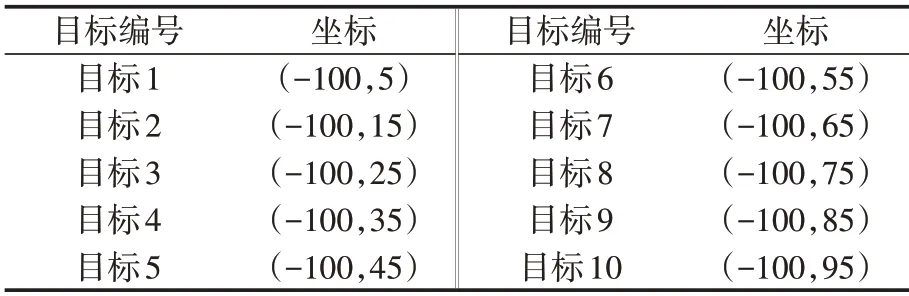
表4 任务目标的坐标Tab.4 Coordinates of task objects

鉴于战场场景的复杂性，估算出的地理坐标未必准确，无人机至任务目标之间的欧式距离具有不确定性，本文将其抽象为1 个区间数。假设任意1 个区间数的上界和下界是随机变化的（每次实验都不相同），且最大抖动范围不超过10。例如，在确定环境中，无人机1 与任务目标1 之间的欧式距离固定为200.062 5。由于战场环境的不确定性，将该飞行距离抽象为1个区间数（200.062 5-10×randL，200.062 5+10×randR），其中，randL和randR表示区间（0，1）内均匀分布的2 个随机数。

实验中，3 种多变异差分进化的参数如4.1 节所述，此处不再赘述。

4.2.2 算法有效性实验

以性能最优的DE-MM2为例，讨论差分进化算法求解不确定环境下多无人机任务分配问题的有效性。

多次仿真实验表明，DE-MM2能够快速地求解此类多无人机任务分配问题。鉴于区间数取值的随机性，每次实验结果具有显著的差异。下面，以1次实验为例，详细分析实验结果。假设DE-MM2求得最优解xopt=(1 2 4 3 7 6 5 10 9 8 )，据此能够获得最优分配方案，如图4所示。图中，右侧五角星表示各架无人机的位置，左侧星号表示各个攻击目标的位置。与之相对地，在确定环境的场景中，无人机和攻击目标之间的距离是确定的，那么，最优的无人机任务分配方案xopt=(1 2 3 4 5 6 7 8 9 10 )。可以认为，不同场景下（确定环境和不确定环境）实验结果的差异性，恰好体现了多变异策略差分进化算法的有效性。

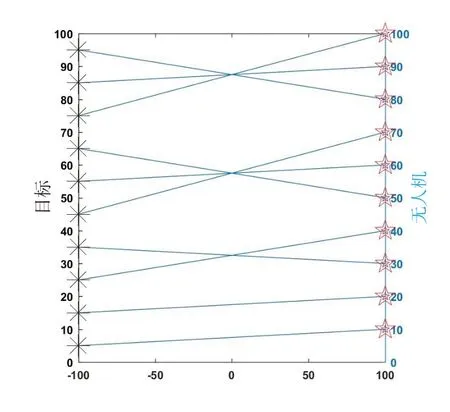
图4 最优无人机任务分配方案Fig.4 Optimal solution of task allocation for multi-UAV

如前所述，在计算适应度时，多变异策略差分进化算法每次都会得到2 个适应度值，分别为适应度上界和下界。它们的变化趋势如图5 所示。图中显示，适应度曲线并未持续性地单调下降，而是呈现抖动状态。这是因为，每个候选解获得的适应度都是1 个区间数，2个区间数往往存在较大范围的重叠部分，它们之间的比较大小是基于概率的（如2.4 节所述）。因此，此时的选择操作并不能保证最优解所对应的适应度持续性地单调下降。

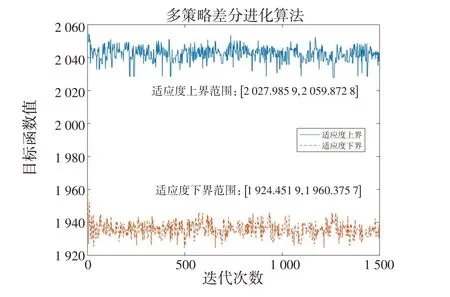
图5 适应度上界和下界的变化趋势Fig.5 Variation trends of the upper bound and lower bound of fitness values

4.2.3 算法性能对比实验

本节对比3 种多变异差分进化算法，求解此类多无人机任务分配问题的算法性能。

3 种多变异差分进化算法独立运行20 次，求得的适应度上界和下界的变化区间如表5所示。须要指出的是，在每次独立实验中，区间数的上界和下界都是随机选择的，而且3种算法运行时，这些（随机的）初始实验取值保持不变，以尽可能消除实验参数对算法性能的影响。

由于适应度的上界最大值和下界最大值都容易受到初始种群构建的影响，本文重点考查了适应度的上界最小值和下界最小值。在表5 中，各种算法中表现最优的结果，用粗体表示。根据表5的结果，可以发现，DE-MM2 获得了14 次最优的上界最小值和18 次最优的下界最小值，略多于DE-MM3的14次和15次，显著多于DE-MM1 的3 次和5 次。依据这20 次独立实验的平均值，DE-MM2获得的适应度的上界最小值（2 030.5281）和下界最小值（1 929.640 6）都是最优的，DE-MM3 次之，DE-MM1 性能最差。整体来看，该实验结果与4.1节求解函数优化问题得到的结论是一致的。

5 结束语

不确定环境下多无人机任务分配已经成为无人机集群之间的协同配合场景下的1 个热点研究方向。本文将无人机与攻击目标之间距离的不确定性抽象为1 个区间数，并构建了不确定环境下多无人机任务分配的数学模型。综合考虑各种变异策略的技术特征，设计了3种多变异策略差分进化算法，实验结果验证了改进思路的有效性。采用改进的差分进化算法求解多无人机任务分配问题，实验结果体现了多变异策略差分进化算法的有效性。