基于改进凸包检测算法的多幅芯片图像校正方法
朱俊杰,巢渊,马成霞
(江苏理工学院机械工程学院,江苏常州 213001)
随着电子市场的快速发展,半导体芯片的应用越来越广泛,需求也在不断增加,传统的人工抽检方法已难以满足表面贴装芯片高速高精度检测的需求[1]。机器视觉技术以其高效率、高精度、高可靠性、非接触性和客观性强等优点,在芯片封装模块检测方面得到了广泛研究和应用[2]。由于图像采集系统捕获的目标并非规则地出现,因此,在进行芯片封装缺陷视觉检测前,需要对芯片图像进行旋转校正,以提高后续检测的正确率以及基于缺陷检测的芯片分选效率[3]。
图像倾斜校正算法研究的重点在于倾斜角度检测。杨立刚等人[4]通过Hough 变换精确定位车牌位置,再利用Radon 变换获取车牌的倾斜角度,但此方法中Hough 变换和Radon 变换计算量大,校正效率较低。汪敏倩等人[5]通过车牌图像投影方差的规律性提取局部特征来获得车牌水平倾斜角度或垂直错切角度,但对于局部规律性不明显的图像,此方法难以获取精准的倾斜角度。胡人伟等人[6]运用傅里叶变换将商标图像从空域转换到频域,再通过Hough 变换求出频谱图像中的倾斜角度,以实现图像的倾斜校正;此方法虽然只做了一次空域到频域的变换,但耗时较长,实用性不强。邓翔宇等人[7]通过大尺度梯度下降法实现简谱的粗校正,再利用小尺度梯度下降法进行精细调整;但是当倾斜角度超过±8°时,该方法校正精准性下降明显。李青等人[8]结合Canny 边缘检测和Hough 变换获取交通标识牌矩形边缘的4 个角点坐标,再应用透视变换对其进行校正;但该方法中Hough变换耗时长,且较为依赖Canny 边缘检测获取的图像边缘,不适用于背景复杂的图像。
倾斜角度检测方法耗时长、难以获取精确角度,而凸包检测则可以通过叉乘、角度和长度等方法精准筛选凸包顶点,获取包含位置和角度信息的特征点[9]。黄珂等人[10]通过Harris角点检测算法获取QR 码图像的角点并进行凸包检测,以获取QR 码位置信息;但角点检测过于依赖拍摄的图像,难以获取复杂背景图像的有效角点,且参与凸包筛选的角点数量较多,耗时长。郭亚盛等人[11]运用Andrew 算法获取圆柱类零件图像轮廓凸包,再获取凸包的最小外接矩形以实现对圆柱类零件图像的尺寸测量;但凸包筛选边缘点较多,计算时间较长,且存在特征点集簇拥情况。王亚杰等人[12]提取棋盘轮廓边缘点后,运用凸包检测算法获取棋盘4个顶点坐标,以实现棋盘校正;但该方法需要筛选的棋盘轮廓边缘点较多,计算时间较长。朱俊卿[13]采用基于凸包检测的矩形顶点检测方法定位矩形的4个顶点,采用透视变换对畸变图像进行校正;但该方法需要进行凸包筛选的点集较多,耗时长。
针对凸包检测耗时长、特征点多的问题,彭志光等人[14]改进凸包算法,对叶片型截面点云数据进行排序和精准分割,通过矩形区域腐蚀法确定凸包边界区域,删除冗余点,以减少参与排序和生成凸包的点集数量,提高构造凸包效率。张勇等人[15]根据图像分辨率确定扫描行数,保留扫描行第一个和最后一个像素点形成点集,以提高构造凸包效率。蔡文婷等人[16]对二维条码的边缘点集进行预处理,滤除二维条码内部的点集,再对剩余点集构造凸包,从而实现图像的高效定位。
在图像倾斜校正算法研究中,旋转变换矩阵的选择也是校正的关键。旋转变换矩阵通常有三种:一是二维欧式变换矩阵[17],该矩阵包括平移、旋转和缩放三个基本变换矩阵,可用于对平面图形进行倾斜校正;二是仿射变换矩阵[18],该矩阵是在二维欧氏变换矩阵的基础上增加了一个错切变换矩阵,从而能够更加精确地对图像进行倾斜校正;三是透视变换矩阵[19],该矩阵在仿射变换矩阵的基础上增加了一个透视变换矩阵,能够对三维场景进行投影并进行倾斜校正。相较于二维欧式变换矩阵,仿射变换矩阵可更精确地校正倾斜图像。相较于透视变换矩阵,仿射变换可以保持直线的平行性,从而很好地保持图像的形状,而透视变换会改变图像的形状和大小,容易引起失真。
基于上述分析,本文通过标记多幅芯片图像中每个芯片的位置,改进Andrew 算法以获取倾斜角度和旋转中心,运用仿射变换实现多幅芯片图像的快速校正与提取。
1 图像预处理
半导体芯片在封装过程中存在尺寸公差,制造料盘承载口时会留有一定余量,导致芯片放置于承载口时存在一定程度的倾斜[20]。本文以QFN芯片引脚面图像为研究对象,为了减少噪声的影响,需要对图像进行预处理,获取芯片中心焊盘和引脚边缘点简化图像信息,减少后续处理的计算量。多幅倾斜芯片图像的预处理包括高斯滤波、灰度化和Canny边缘检测。如图1所示,为预处理流程图。

图1 预处理流程图
具体步骤为:
(1)采用3×3 高斯滤波器对图像进行卷积,以平滑图像,减少噪声对后续边缘检测的影响。
(2)对图像进行灰度化处理,以减少后续处理计算量。
(3)为减少噪声影响,获取芯片中心焊盘和引脚边缘点,采用Canny 边缘检测算法,设定低阈值为100,高阈值为200。
2 基于改进凸包检测算法的多幅芯片图像校正方法
常见的凸包检测算法有Graham 扫描法[21]、Andrew算法[22],其中Andrew算法是对Graham扫描法的优化。Graham 扫描法中需要对两个点算出叉乘,甚至在某些情况下还要算出两个点的距离,复杂度较高且极角排序会造成丢点现象,而Andrew 算法直接通过对点(x,y)排序就可以实现,降低了算法复杂度且解决了丢点的问题[23];但Andrew 算法在构造凸包时,存在特征点过多和计算时间较长等问题。因此,本文对Andrew算法进行改进。
2.1 Andrew算法
假设同一平面内3 个不重合的点A=(XA,YA)、B=(XB,XB)、C=(XC,YC),记AB为点A指向点B的向量,AC为点A指向点C的向量。那么,向量AB=(XB-XA,YB-YA) ,向量AC=(XC-XA,YC-YA)。两者叉积为:式中:T被称为点C相对于点A和点B的凸度,通过判断T的正负,可以确定这3 个点的相对位置。如图2所示,根据A、B、C这3个不重合点的相对位置,凸度T有3种情况:

图2 A、B、C三个不重合点相对位置情况
(1)若T(A,B,C)<0 ,则AB顺时针转向AC,如图2(a)所示。
(2)若T(A,B,C)=0,则A、B、C三点在同一直线上,如图2(b)所示。
(3)若T(A,B,C)>0 ,则AB逆时针转向AC,如图2(c)所示。
Andrew 算法通过对点(x,y)排序确定构造凸包的起始点和终点,点集按照点横坐标x从小到大排序,在横坐标x相同的情况下,再按照点纵坐标y从小到大排序。如图3 所示,为采用Andrew 算法构造凸包的示意图。从排序后的第一个点p1到排序后的最后一个点pn,通过判断凸度T大小顺时针构造凸包上部;再从排序后的最后一个点pn到排序后的第一个点p1,通过判断凸度T大小顺时针构造凸包下部;合并凸包上部和下部保留其中一个的起点和终点,获得完整的凸包。

图3 Andrew算法构造凸包示意图
2.2 Andrew算法改进思路
由Andrew 算法构造凸包的方法可知,当芯片的倾斜方向不同时,构造凸包上下部的点集不同。为了提高凸包算法的效率,本文通过设计新的点集排序方式,使芯片中心焊盘左下角、右下角和右上角3个拐角的边缘点在Andrew算法构造的凸包下部,以省去获取凸包上部点集环节,从而大幅度减少凸包计算量。
针对Andrew 算法筛选出的凸包点集存在边缘点簇拥情况,首先通过限制凸度大小减少凸包点集的数量;再设计新点集的排序方法对筛选后的凸包点集进行排序,滤除不需要的凸包点集。如图4 所示,为改进的Andrew 算法步骤示意图。具体步骤为:
(1)设计新的点集排序规则,以坐标系原点为旋转中心将图像逆时针旋转45 ° ,然后将点从下往上排序。 经过排序之后,得到序列φnew:p1,p2,…,pn,其中 p1是中心焊盘左下角的点,pn是中心焊盘右上角的点。如图4(a)所示,为点集排序示意图。
(2)创建3 个拐角边缘点点集序列ν,并在序列ν 中加入点p1。
(3)从第1 个点p1到最后1 个点pn逆时针构造凸包下部得到凸包点集。如图4(b)所示,为构造凸包下部示意图。可以看出,连接凸包下部需要筛选的边缘点为L 型。序列φnew: p1,p2,…,pn中的点从p1开始逐个加入序列τ ,若序列τ 中的点多余1 个,取出序列τ 中最后2 个点,设定当前点pi和序列τ中最后2 个点的凸度T(τlast-1,τlast,pi) 大小为20。若设定凸度的值较小,筛选的凸包点集将过多,不利于后续筛选;若设定的凸度值较大,则存在筛选后的凸包点集中,不能将3 个拐角点都包含在内的情况。 经过测试,选择凸度T(τlast-1,τlast,pi)为20,这样,筛选的凸包点集中能够包含3 个拐角点,且点集数量较少。判断T(τlast-1,τlast,pi) 是否大于等于设定值,若T(τlast-1,τlast,pi)小于等于设定值,则删除序列τ 中最后1 个点;若T(τlast-1,τlast,pi) 大于等于设定值,则将当前点pi加入序列τ 的最后。
(4)在序列ν 中加入点τlast。
(5)为了保证能精准获取L 型边缘点的拐角边缘点,设计新的点集排序规则,以坐标系原点为旋转中心将图像顺时针旋转45°,然后将点从下往上排序。如图4(c)所示,为序列τ 的点集排序示意图。将序列τ 的点集进行排序,取出排序后的第1个点加入序列ν。
(6)在序列ν 中获取芯片中心焊盘左下角、右下角和右上角3个拐角边缘点。
由上述步骤可知,该方法不仅适用于QFN封装芯片倾斜角度的快速获取;而且对于和芯片中心焊盘相同类型、可通过水平或垂直轮廓线来表示倾斜角度、且存在L 型轮廓边缘点的图像,也可以应用该算法快速获取倾斜角度。
2.3 多幅芯片图像校正
本文通过改进Andrew 凸包检测算法,快速获取多幅芯片的倾斜角度和旋转中心,校正多幅芯片图像。如图5 所示,为多幅芯片校正方法流程图。具体步骤为:
(1)预处理。根据本文第1 节预处理方法,完成多幅芯片倾斜图像的预处理,获取每个芯片的边缘点。
(2)边缘点筛选。筛选出中心焊盘轮廓边缘点,剔除非中心焊盘轮廓点。本文通过限制Canny边缘检测获取的边缘点个数,保留边缘点个数小于500 或大于2 000 的轮廓,筛选出中心焊盘的轮廓边缘点,滤除其余轮廓边缘点。
(3)记录芯片位置信息。为后续应用ROI 感兴趣区域提取校正后的图像,本文采用最小外接正矩形标记每个芯片位置信息。当得到目标对象轮廓后,获取包覆此轮廓的最小正矩形,并记录其左上角坐标和长宽。
(4)获取倾斜角度和旋转中心。为了获取每个芯片的倾斜角度,本文提出改进Andrew 凸包检测算法,筛选凸包点,获取每个芯片中心焊盘左下角、右上角和右下角3个拐角的边缘点。计算芯片中心焊盘左下角拐角点和右下角拐角点坐标组成的向量与坐标x轴之间的夹角,即每个芯片的倾斜角度。设两个坐标点分别为p(x,y)、q(x,y),则图像倾斜角度θ计算公式为:
式中:xp和yp为点p的横坐标和纵坐标;xq和yq为点q的横坐标和纵坐标。为了获取每个芯片的旋转中心,应用改进Andrew 凸包检测算法筛选凸包获得中心焊盘左下角边缘点和右上角边缘点,两者连线的中心点即旋转中心。
(5)校正倾斜芯片图像。基于改进Andrew 凸包检测算法获取多幅芯片倾斜角度,且以每个芯片形心为旋转中心获得仿射变换矩阵,通过仿射变换矩阵将倾斜图像上的每个点进行旋转校正。在二维空间内,常见的旋转变换矩阵有两种:一种为绕原点旋转;另一种为绕任意点旋转。绕原点旋转的旋转变换矩阵简单直接,但图像旋转中心不在原点,需先将图像移动到原点再进行旋转,该操作将增加计算量和实现难度。相比之下,绕任意点旋转可以直接指定旋转中心点的坐标,方便灵活。由于通过改进Andrew 算法已经获取了芯片的倾斜角度和旋转中心,因此,本文将芯片图像绕旋转中心旋转以实现校正。设旋转中心为(x,y),倾斜角度为θ弧度,绕旋转中心逆时针旋转θ的旋转变换矩阵M1计算公式为:
绕旋转中心顺时针旋转θ的旋转变换矩阵M2计算公式为:
设倾斜图像上的点为(x1,y1),旋转变换矩阵M为M1或M2,旋转后图像上的点(x2,y2) 计算公式为:
(6)提取校正后的芯片图像。根据最小外接正矩形标记每个芯片位置信息,以芯片的左上角坐标和芯片的长宽设定矩形ROI 区域,进而提取校正后多幅芯片图像的矩形ROI区域。
3 实验结果与分析
3.1 实验结果
本文通过改进凸包检测算法实现多幅芯片图像校正,解决了传统方法在处理多幅芯片图像时必须先进行图像切分才能够继续校正的问题[20],从而有效提高了多幅图像的校正效率。选取10 幅不同的多幅QFN 芯片引脚面图像为实验对象,每幅图像中包含9 个QFN 芯片,共90 个QFN 芯片。实验环境为四核十二线程、CPU@2.2 GHz、内存16 G、Visual Studio 2017。如图7(a)所示,为多幅芯片倾斜图像。如图7(b)至7(j)所示,为校正后的多幅芯片图像,其分别对应多幅芯片倾斜图像中第1 至第9 个芯片。由图7 可见,对于一幅包含9 个不同芯片的多幅QFN 芯片引脚面图像,本文方法能够省去单幅芯片图像的切分环节,直接完成每个芯片的校正与提取。

图7 采用本文方法校正多幅芯片图像
3.2 算法对比
3.2.1 时间对比
对于多幅芯片图像,传统算法需要先切分,再对切分后的单幅芯片图像进行校正。如图8所示,为了检测切分多幅芯片图像的运行时间,本文对采集到的9 幅多幅芯片倾斜图像进行切分,每幅图像中包含9 个芯片,使得切分后的图像中仅包含单幅芯片。如图8(a)所示,为多幅芯片倾斜图像,如图8(b)至8(j)所示,为切分后单幅芯片倾斜图像,其分别对应多幅芯片倾斜图像中第1 个至第9个芯片。

图8 切分多幅芯片图像
如表1 所示,为9 张多幅芯片倾斜图像的切分时间。从表1 可见,平均切分时间为406.67 ms,平均每个芯片的切分时间为45.18 ms。本文采用最小外接正矩形标记芯片位置信息,应用ROI 完成校正后的芯片图像提取,从而直接省去如表1 所示的45.18 ms 的平均单幅芯片切分时间。

表1 切分多幅芯片图像的时间 单位:ms
为了检测本文方法与传统Hough 变换校正方法[24]、最小外接矩形校正方法[25]、傅里叶变换校正方法[26]的时间差异,分别对9幅不同的QFN芯片引脚面图像进行运行时间对比。为了保证算法对比的有效性,首先,将3 种对比算法都按上述完成芯片倾斜图像的预处理,获取边缘点;接着,获取边缘点最小外接矩形,通过限制最小外接矩形长宽,筛选出芯片中心焊盘轮廓边缘点;最后,通过芯片中心焊盘的最小外接矩形确定旋转中心,该旋转中心即为最小外接矩形的中心点。
传统Hough 变换校正方法通过Hough 变换计算芯片中心焊盘水平或垂直轮廓线的倾斜角度,再应用仿射变换校正芯片图像。最小外接矩形校正方法通过最小外接矩形获取芯片中心焊盘的倾斜角度,再应用仿射变换校正芯片图像。傅里叶变换校正方法通过最小外接正矩形标记芯片中心焊盘位置信息,设定矩形ROI 区域提取芯片中心焊盘图像;再应用傅里叶变换求出芯片中心焊盘频域图像,应用Hough 变换计算频域图像中直线的倾斜角度;最后应用仿射变换校正芯片图像。如表2所示,为4种算法的运行时间。对9 幅芯片引脚面图像校正的平均时间,传统Hough 变换校正方法为153.89 ms,最小外接矩形校正方法为120.33 ms,傅里叶变换校正方法为191.89 ms,本文方法处理单幅图像的平均用时仅为45.11 ms;与对比方法中平均用时最少的最小外接矩形校正方法120.33 ms 相比,本文方法的平均用时少于其1/2。由于采用最小外接正矩形标记芯片位置信息,应用ROI 完成校正后芯片图像的提取,省去了单幅芯片图像切分环节,本文方法校正包含9个芯片的多幅芯片图像中每个芯片的平均时间为79.44 ms,与对比方法中校正单幅芯片平均用时最少的最小外接矩形校正方法120.33 ms 相比,本文方法校正多幅芯片图像的平均用时少于其2/3。
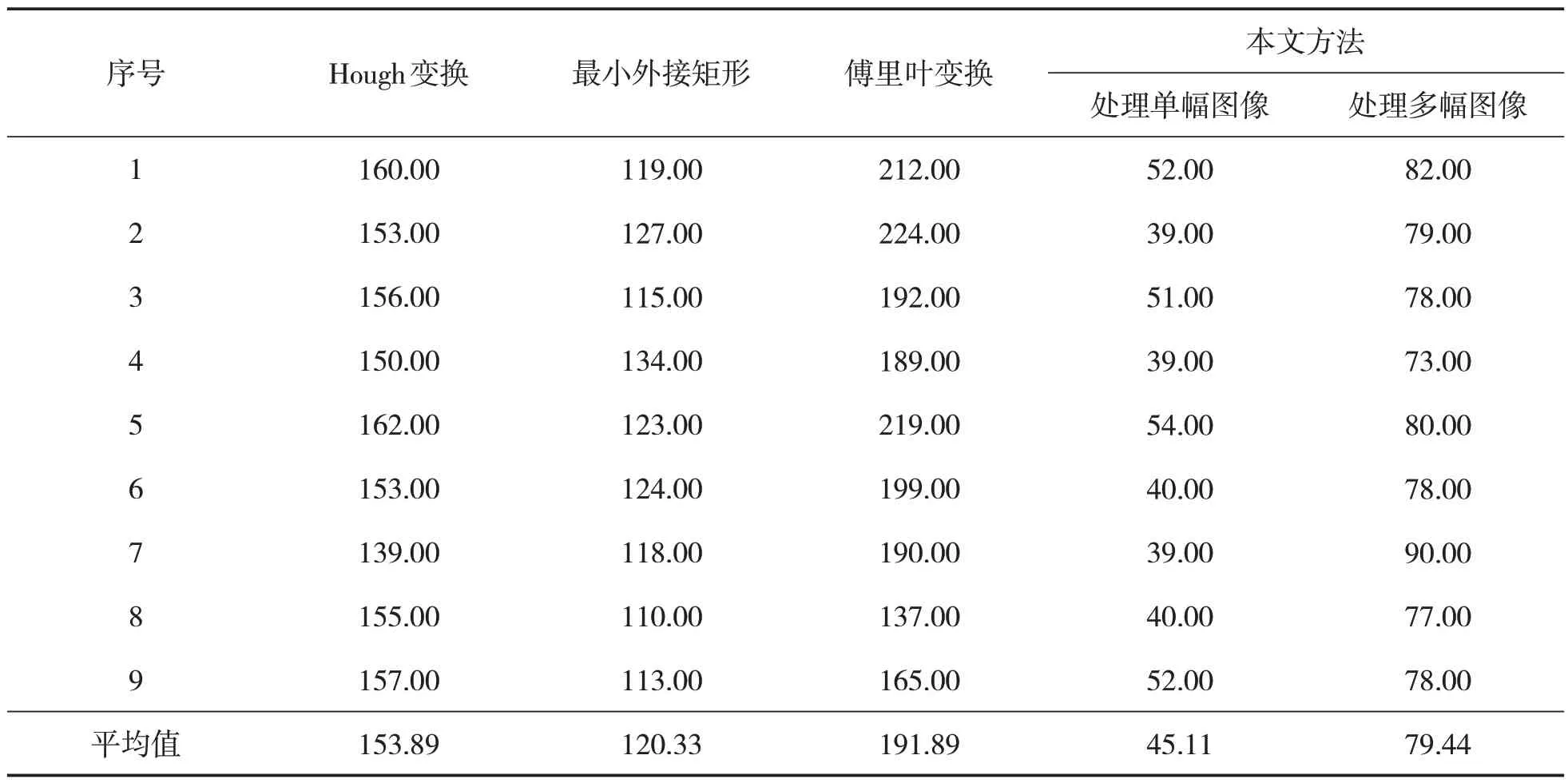
表2 4种算法校正图像的时间 单位:ms
3.2.2 角度偏差对比
如图9 所示,通过人工标定5 幅倾角分别为1°、2°、3°、4°、5°,规格为34 mm×30 mm×9 mm的金属量块图像,对本文方法获取倾斜角度的准确性进行验证。如表3所示,运用上述4种算法分别检测5幅量块图像得到倾斜角度及偏差值。根据表3,本文方法获取的5幅量块图像倾斜角度和人工标定角度的平均偏差为0.085°,低于其它3种对比方法,说明本文方法可以获取相对更为准确的量块图像倾斜角度。

表3 4种算法获取倾斜角度与人工标定角度的误差对比 单位:(°)
为了验证本文方法应用在QFN芯片引脚面图像检测中的准确性,如图10所示,选取一张标准无倾斜的QFN 芯片引脚面图像为实验对象,将此芯片图像每次顺时针旋转0.5°,旋转7 次获取倾角分别为0.5°、1.0°、1.5°、2.0°、2.5°、3.0°、3.5°的7 张标准角度倾斜芯片图像。如表4所示,运用上述4种算法分别检测7张标准角度倾斜芯片图像的倾斜角度及偏差值,平均偏差分别为:本文方法0.112°、传统Hough变换校正方法0.293°、最小外接矩形校正方法0.339°、傅里叶变换校正方法0.753°;本文方法获取的平均偏差小于其它3种对比方法,说明其获取倾斜角度更加准确。

表4 4种算法获取倾斜角度与标准角度的误差对比 单位:(°)

图10 标准角度倾斜芯片图像
4 结论
本文以多幅QFN 芯片图像为实验对象,针对芯片在封装缺陷视觉检测过程中存在的图像倾斜问题,改进Andrew 凸包检测算法,实现多幅芯片图像校正。首先,通过限制轮廓点个数筛选出芯片中心焊盘轮廓,用最小外接正矩形标记每个芯片位置信息;然后,采用改进Andrew 算法快速获取多幅芯片图像中每个芯片的倾斜角度和旋转中心;最后,应用仿射变换校正多幅芯片图像,根据芯片位置信息应用ROI完成芯片图像的校正与提取。实验结果表明,与传统的Hough 变换方法、最小外接矩形方法、傅里叶变换校正方法相比,该方法能够更精准校正芯片图像,且校正单幅芯片图像的运行时间少于对比方法的1/2。
本文方法采用最小外接矩形标记芯片位置信息,应用ROI完成校正后的芯片图像提取,省去了单幅芯片图像切分环节,能够进一步提高图像校正效率。改进的Andrew算法不仅适用于QFN芯片图像,而且同样适用于可通过水平或垂直轮廓线来表示倾斜角度且存在L 型轮廓边缘点的图像。但是,该方法依赖于能够获取连续不间断的L型边缘点,若缺少L型边缘点,则无法获取旋转中心;若边缘点不连续,则会出现两个倾斜角度和旋转中心,影响校正精度。在后续研究中,可研究边缘检测算法以获取连续边缘,再配合本文改进的Andrew 算法,获取存在L型边缘点图像的倾斜角度。

