一道北大保送题的证法探究、背景分析及推广

廖献文

(福建省永春美岭中学,福建 永定 362618)

勃罗卡点(Brocard point)问题自1875年由勃罗卡提出之后,已经有148年之久.在这段历史中,不断有人重新发现并研究它.时至今日,人们围绕勃罗卡点得到了很多结论,丰富了这个问题法的研究成果,使其成为三角形几何学中的一个亮点.2011年北京大学保送生数学考试试题第2题就是以勃罗卡点为背景来进行命制的.笔者经过探究,给出试题的四种证明方法,并将试题进行推广.

1 试题呈现

2011年北京大学保送生数学考试试题第2题如下:

如图1所示,已知△ABC中,∠BAO=∠CAO=∠CBO=∠ACO.求证:△ABC三边成等比数列.

图1 试题题图

分析本题实际上是当点O是(正)勃罗卡点时, 依定义,∠OAB=∠OBC=OCA=θ, 同时又满足∠OAC=θ, 表明OA又是角A的平分线. 实际上, 就是当点O是勃罗卡点时, 又增加了一个条件, 就预示着△ABC满足某些条件.

2 勃罗卡点与勃罗卡角的定义

如图2所示,设点P是△ABC内一点,满足∠PAB=∠PBC=∠PCA=θ,称点P为△ABC的正勃罗卡点,角θ为△ABC的勃罗卡角.

图2 正勃罗卡点(角) 图3 负勃罗卡点(角)

如图3所示,设点P′是△ABC内一点,满足∠P′BA=∠P′CB=∠P′AC=θ,称点P′为△ABC的负勃罗卡点,角θ为△ABC的勃罗卡角[1].

注若三角形给定,则三角形的勃罗卡点是勃罗卡角是存在的.所以,一个三角形有两个勃罗卡点,分别叫做正勃罗卡点和负勃罗卡点,对应的也有两个勃罗卡角. 可以证明,这两个勃罗卡角的大小是相等的,而通常情况下,两个勃罗卡点是不重合的.

3 证法探究

证法1如图4所示, 设∠BAO=∠CAO=∠CBO=∠ACO=θ, 延长AO交△BOC的外接圆O1于点D.由于∠OBC=∠OCA, 因此AC为外接圆O1的切线,C为切点, 所以∠ODC=∠ACO=θ, 故AC=CD.

在△BCD与△ABC中,

∠BCD=∠BOD=∠OAB+∠OBA=∠OBC+∠OBA=∠ABC,

即∠BCD=∠ABC.

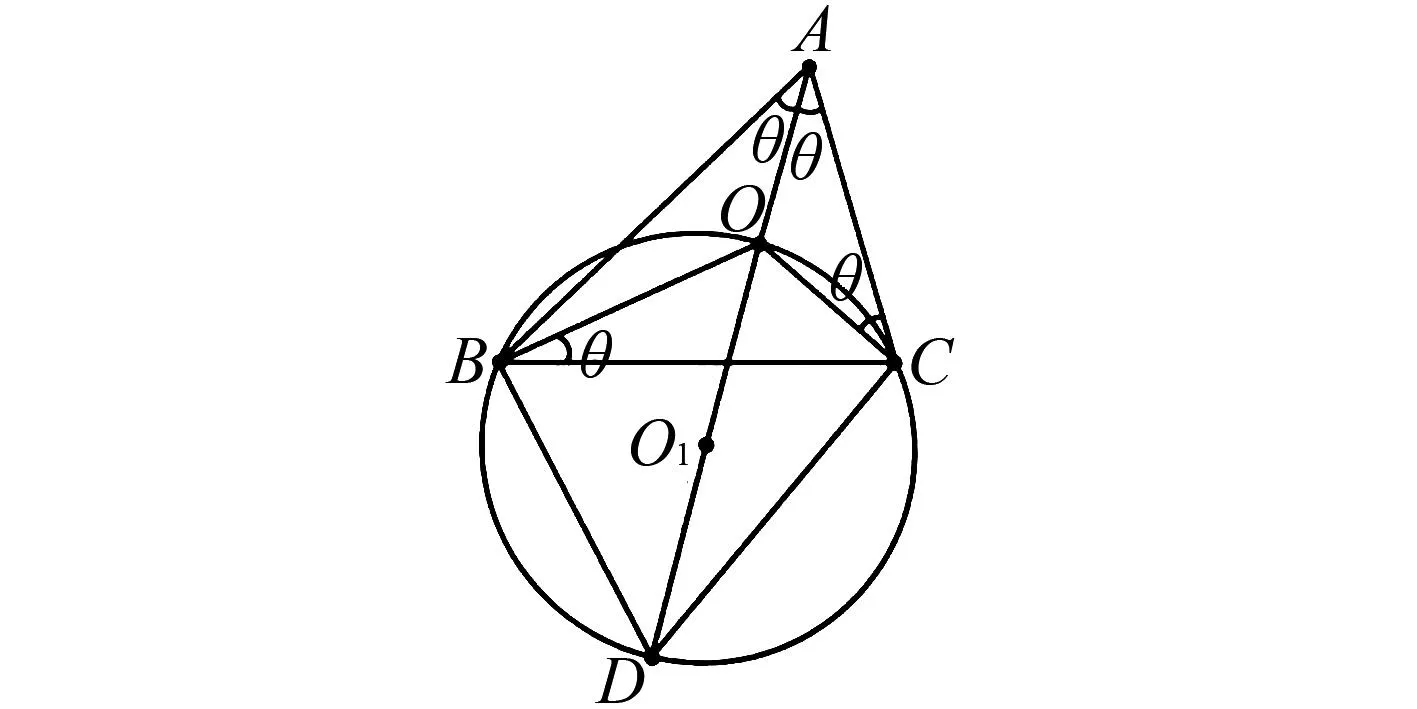
图4 证法1图

又因为cos2θ=cosA=-cos(B+C), 所以1+cos(B+C)-cos(B-C)=cos4θ, 展开得1-2sinBsinC=cos4θ, 即2sin22θ=2sinBsinB, 亦即sin2A=sinBsinC.再由正弦定理得BC2=AB·AC, 即AB,BC,CA成等比数列.

证法3 如图5所示, 对于任意△ABC, 过点A作BC的平行线AD, 作∠ACD=∠ABC, 连接BD, 在BD上取点O, 使得∠OCA=∠ODA=θ.

因为AD∥BC, 所以∠OBC=∠ODA=θ=∠OCA, 则A,D,C,O四点共圆, 所以∠OAC=∠ODC, 而∠BAC=∠ADC, 所以∠OAB=∠ODA=θ, 点O是△ABC的(正)勃罗卡点.

图5 证法3图 图6 证法3图

在图5的基础上,过D,A作BC(延长线)的垂线, 垂足分别为E,F, 得到图6,在△BDE,△ABF,△ACF,△DCE中, 易得

=cotB+cotC+cotA,

即cotθ=cotA+cotB+cotC.

⟺sin2A=sinBsinC.

再由正弦定理得BC2=AB·AC, 即AB,BC,CA成等比数列.

证法4如图1所示, 在△AOC中,∠AOC=π-θ-θ=π-2θ.

①

在△BOC中,∠BOC=π-C,

由正弦定理得

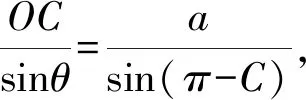
②

在△AOC中OA=OC.

结合式①、式②得

为了确保抛光过程覆盖的均匀性，Rososhansky等[39]在光栅轨迹规划方法当中引入柔性抛光头与工件的弹性接触变化。文献[40] 中针对光栅轨迹抛光引入行距适应算法，将该方法应用于自由曲面加工中，提高了抛光轨迹覆盖的均匀性。

即AB,BC,CA成等比数列.

4 试题推广

实际上, 我们得出下列结论:

结论1 已知△ABC中(见图1),∠BAO=∠CAO=∠CBO=∠ACO=θ, 则A=2θ⟺OA=OC⟺a2=bc.

我们知道, 一个三角形有两个勃罗卡点. 在本题中,O是正勃罗卡点, 且满足条件∠BAO=∠CAO=∠CBO=∠ACO=θ.如图7所 示, 若引人O′是负勃罗卡点, 即满足条件∠O′BA=∠O′CB=∠O′AB=∠O′AC=θ′. 利用证法 3 中同样的方法, 对负勃罗卡角θ′, 同样可得cotθ′=cotA+cotB+cotC, 所以cotθ=cotθ′, 即θ=θ′, 则AO,AO′都是A的内角平分线, 即A,O,O′三点共线, 且O′A=O′B.于是得到结论2.

图7 正、负勃罗卡点

结论2已知在△ABC中,O,O′分别是正、负勃罗卡点, 且各自满足:∠BAO=∠CAO=∠CBO=∠ACO=θ,∠O′BA=∠O′CB=∠O′AB=∠O′AC=θ′.则

(1)θ=θ′;

(2)A=2θ⟺OA=OC⟺O′A=O′B⟺A,O,O′共线.

回顾试题,我们发现试题实际上给出了三边成等比数列的三角形的勃罗卡点的一个性质, 容易想到的问题是:如果△ABC三边成等差数列, 那么相应的勃罗卡点有什么特殊性质呢?

下面研究三边成等差数列的三角形的勃罗卡点问题. 以下问题中, 三边成等差数列, 就是指a,b,c成等差数列.

首先我们给出如下引理:

其中a,b,c是△ABC三个内角A,B,C所对的边.引理1和引理2的证明参见文献[2].

结论3 在△ABC中,α是勃罗卡角,P是正勃罗卡点,Q是负勃罗卡点, 则

结论4 在△ABC中,α为正勃罗卡角,则

a2,b2,c2成等差数列⟺cotA,cotB,cotC成等差数列⟺cotα=3cotB.