基于时间序列预测的物料生产安排研究
郝 鹏
(山西机电职业技术学院 基础部,山西 长治 046000)
2019年以来,全球经济负向走势显观,我国某电子产品制造企业面临在多品种小批量物料生产中事先无法了解物料实际需求量的问题,需使用数学方法进行历史数据分析,对着重关注的物料(需从物料需求出现的频数、数量、趋势及销售单价等方面考虑)创建需求周预测模型(以周为基本时间单位,预测物料的周需求量),运用历史数据评价预测模型,帮助企业合理安排物料生产。对数据进行预处理,对异常数据进行分析处理,得到每种物料每周的用量与数据及每种物体周用量的变化图及数据的周期特征,选取特征,利用TOPSIS进行重点目标物料的选取,基于数据的时序周期特性建立Prophet时间序列模型,计算平均相对误差MSE,来评价模型的优劣,具体步骤如图1所示。

图1 具体步骤Fig.1 Detailed procedures
利用Prophet时间序列模型预测后续周期的库存量、缺货量、服务水平及非零周量,根据此方法求出相应的的生产计划数、实际需求量、库存量、缺货量、服务水平及非零周量。选取前n个数据进行模型训练,对第n+m周的生产计划进行预测。绘出6种物料的平均生产计划、平均实际需求、平均库存量、平均缺货量、平均服务水平与非零周数等数据及各物料的生产计划预测,其中平均服务水平为:

1 模型建立与求解
1.1 物料选取
对数据进行预处理,在时间尺度上,根据物料采购的时间特性用Python中的datetime库对数据进行时间处理,得到以天为单位和以轴为单位的时间间隔数据。在物料预定方面,对所有物料商品的订购数据进行处理分析,考虑中间存在周数据缺失的情形,为保证周数据连续,结合企业实际对缺失数据的周次进行赋0处理,得到每种物料的完整周期数据。统计出每种物料周用量及采购金额数据后,以时间为横轴,以物料用量,为纵轴绘制用量趋势。无周期性示意图如图2,有周期性示意图如图3。

图2 无周期性物料周用量趋势Fig.2 Aperiodic weekly material consumption trends

图3 有周期性物料周用量趋势Fig.3 Periodic material consumption trends

图4 多值时间序列预测Fig.4 Multi-valued time series prediction
观察可知,数据量少、周期性不明显的数据对于预测没有效果,而周期性强、数据丰富的物料有利于生产安排的提前预测。充分考虑物料的需求用量、金额及周期性,以这些因素为指标选定考察对象,选取讨论物料需求出现的频数、数量、趋势、销售单价及非零周量,将其用来进行物料数据筛选,得出每种物料不同指标的计算公式如下:
当N=177时,物料需求出现的频数为:
(1)
N表示总周数,mi为该物料第i周的用量。
物料总量为:
(2)
平均趋势为:
(3)
销售单价为:
(4)
其中,pi为第i种物料的使用金额。
非零天数为:
T=∑ti(ti=1或0)
(5)
选用TOPSIS对数据进行选择。
TOPSIS综合评价法利用已给出的数据准确反映出各评价方案之间的差距,在实际方案选择过程中充分利用数据本身的特性,而不是从人为主观角度来确定样本排序,目前已广泛应用于综合评价类问题中。根据TOPSIS的评价过程及指标优劣来评判方案可知,物料的频数、数量、趋势、销售单价及非零周量均为效益型属性,即属性值越大代表该方案越好。由于不同指标的单位不尽相同,为了将所有指标在同一尺度下进行比较,需要对数值进行归一化,所有指标数据均为正值,故采用线性变化进行操作。

(6)
xij为第i种物料第j个指标的实际数值。
向量规范化用式(7)进行变换:
(7)
变换后,属性值的大小上无法直接分辨属性值的优劣,各方案的同一属性值的平方和为1,计算各方案与某种虚拟方案(如理想点或负理想点)的欧几里得距离的场合。
构造加权规范阵为:
R=(rij)m×n
设给定每各指标的权重向量为[0.15,0.15,0.15,0.15,0.4],记为u=[u1,u2,u3,u4,u5],则:
rij=ui·yij,i=1,2,…,m;j=1,2,…,n
(8)

(9)
定义最小值:
(10)

(11)
(12)
(13)
计算排序指标值Fi,由值的大小可以确定各方案从好到坏的排序。
计算可知,排名前6的为6004020503、6004020908、6004010256、6004020656、6004100008、6004020374。
1.2 时间序列预测
根据数据的周期特征,利用Prophet时间序列算法对数据进行预测建模。
此模型预测示意图为滑窗模型,因为需要预测的结果在原数据结构种是连续排列的,故需通过之前的数据f将预测值K周预测出来,进而预测未来的数据。
Prophet对具有强烈周期性特征的历史数据拟合效果很好,可处理时间序列存在一些异常值的情况及部分缺失值的情形。
对数据进行周期性预测,利用傅里叶变换估计出周期的可能性,如表1所示。

表1 周期估计Tab.1 Period estimation
根据表1数据可以读出此6种物料中59占周期频率最多,故选取60作为周期参数。
选取滑动窗口60个作为周期参数,对6种物料进行预测,得到预测均方误差及平均相对误差,如表2。

表2 预测均方误差及平均相对误差Tab.2 Prediction mean square error and mean relative error
对于时间序列模型来说,在均方误差效果显示模型效果良好,平均相对误差相对较差。
Prophet适用于具有明显的内在规律的数据,对于题目中所给数据,基于分段线性函数的趋势项进行预测,算法模型为:
g(t)=[k+α(t)Tδ)·t+(m+α(t)Tγ]
(14)
其中,g(t)表示增长趋势项,表示时间序列在非周期上面的增长变化趋势;α表示滑动窗口,k表示增长率;δ表示增长率的变化量;m表示偏移量。
运用傅里叶级数近似这个周期属性。
根据题目要求需进行以周为基本单位的周期预测,其傅立叶级数的形式为:
(15)
N表示模型中使用这种周期的个数,对训练集来说,较大的N值可以拟合出更好的效果,但是容易出现过拟合,且泛化能力会降低。
按照经验值,对于以一周为周期的序列N=3时,有:
(16)
因此时间序列的周期项为:
s(t)=X(t)β
(17)
其中,β是服从标准正态分布的随机数。
根据以上模型预测出其结果与原始图数据的比较,如图5所示。
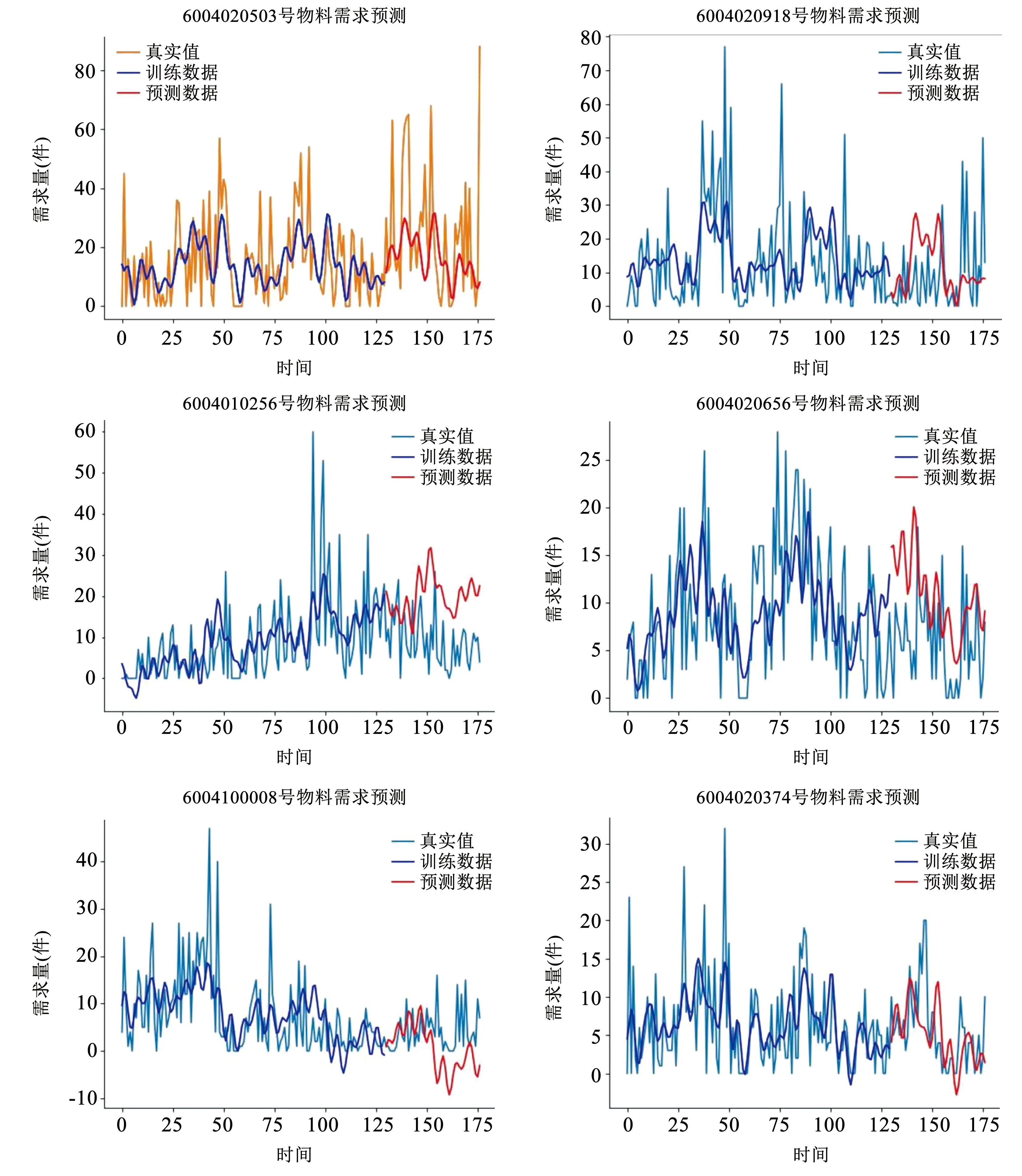
图5 预测结果与原始图数据的比较Fig.5 Comparison of prediction results with original graph data
从图5可以看出,预测总体趋势与原始数据较为吻合,故建立的模型是合理的,可用来进行需求量预测。基于Prophet的时间序列模型可以得到6种物料的每周计划数,包括平均生产计划、平均实际需求量、平均库存、平均缺货、平均服务水平,如表3所示。

表3 6种物料第101~177周的平均值Tab.3 Average value of 6 kinds of materials in week 101~177
由表3数据可知,此模型的平均服务水平均不低于工厂生产需求的85%要求,满足工厂要求。
2 模型检验
根据建立的Prophet时间序列预测模型可知,滑动窗口的选取对预测结果往往具有较大的影响,选用的滑窗模型将滑动窗口参考值由60改为30,观察模型的灵敏性,重新训练模型进行预测,计算均方误差及平均相对误差,如表4。

表4 均方误差与平均相对误差Tab.4 Mean square error and mean relative error
由表4结果可知,对于时间序列模型来说,平均相对误差相对改进前较为理想,均方误差效果显示,模型效果不太理想。
——HeightsTM用高效率和智能化提升服务水平

