基于粒子群算法的点云特征拼合方法*

束 怡，翟欢乐

（江苏航空职业技术学院工程学院，江苏镇江 212000）

0 引言

在逆向工程中，数据采集和处理是实现三维模型重建的第一步工作，数据采集也称零件的数字化，是通过特定的扫描设备和扫描方法获取零件表面离散点的几何坐标数据，这些几何坐标数据称为点云，在此基础上进行复杂曲面的建模、评价、改进和制造，点云数据处理的好坏程度直接影响整个逆向设计过程的精度[1]。点云数据常用采集方法有CMM 坐标测量、激光扫描等，受测量技术、周围环境、物体几何形状、定位以及夹具等因素的影响，通常需要对物体进行多方位测量，然后将不同方位下测的点云拼合成一个表达完整实物的点云，最后通过模型重建方法生成零件的三维模型[2]，然而这些方法获取的测量物体表面数据点信息有限，需要进行多次测量。点云的拼合过程就是根据点云间的共有特征信息，设定评判准则，求解坐标系变换的旋转矩阵和平移矩阵，以将所有点云拼合在同一坐标系下[3]。

点云拼合主要分为两种方式，一种是基于点云的直接拼合，如最常见的ICP 算法[4]，该算法是将目标点云P与源点云Q 进行比较，匹配得到最接近的点云对，再进行相关运算得到误差函数，并计算出使得误差函数最小的参数旋转矩阵R和平移向量t。在此基础上，再对目标点云P 进行旋转和平移变换，得到新的对应点集P′，随后不断重复该过程直到目标收敛条件达成。除了应用最广泛的ICP 算法，还有Horn[5]提出的四元数法，刘宇[6]提出的基于法矢的点云拼合方法，孙世为[7]提出的基于曲率RGB 的多视点云拼合方法等；另一种是基于参考点的间接拼合，孙殿柱[8]、程俊延[9]等通过在零件上粘附一些固定球或者标签，完成点云的拼合。

基于点云的直接拼合，优点是拼合精度高，缺点是计算难度大、成功率低；基于参考点的间接拼合，优点是拼合简单、成功率高，缺点是新增物在一定程度上覆盖了原有零件的部分表面，为后期逆向设计增加了难度[10]。鉴于此，本文基于零件原有的平面、直线或点特征来研究点云的拼合方法，并引入粒子群算法来提高拼合效率。

1 数据测量与处理

1.1 点云及几何特征的测量

零件表面测量可分为接触式测量与非接触式测量两种方式，接触式测量主要用不同类型的机械探头接触需要测量的物体表面，通过机械臂上的传感器得到相对坐标位置，最终得到测量零件的特征信息；非接触式测量则是使用类似光学、声学等领域的原理知识，再将得到的物理模拟量转化为测量零件的表面信息[11]。关节臂测量机集两种测量方式于一身，每次的测量数据可同时包含特征数据及点云数据，根据特征信息完成坐标系变换，即完成了点云数据的拼合。

测量时，会有环境、零件形状、零件放置方式等因素影响测量结果，因此在测量之前，要做好规划工作，以起到降低误差的作用，一是判断零件表面的颜色是否会产生镜面反射，再确定扫描次数及放置方式，遵循全面性及稳定性原则，将复杂面朝向容易扫描的方向；二是确定要测量的特征，确保所选的特征比较精确、距离相对较远且能够使点云拼合方式唯一[12]。零件放置方式的规划与特征的选择相互影响，要综合考虑，权衡取舍。

1.2 数据处理

通过关节臂测量机测量的平面特征可用4 个点来表达，直线特征可用2个点来表达。以2次扫描测得的数据进行分析，可分别写成数据集合A={MAI,XAJ,DAK,YAM}，B={MBI,XBJ,DBK,YBN}，其中MAI、MBI均代表I个特征平面组成的集合，分别用4I×3矩阵表示；XAJ、XBJ均代表J个特征直线组成的集合，分别用2J×3 矩阵表示；DAK、DBK均代表K个特征点组成的集合，分别用K×3 矩阵表示；YAM代表M个点组成的点云集合，用M×3矩阵表示；集合YBN代表N个点组成的点云集合，用N×3矩阵表示。

数据集合A中的MAI、XAJ和数据集合B中MBI、XBJ无法直接通过坐标变换建立重合关系，需要变换表达方式，用方向向量和点坐标来表示[13]。其中，方向向量根据特征点的相对位置确定唯一性，点坐标通过特征点在平面或直线上到投影获得。因此，集合A和B可采用新的表达方式：A={UA,WA,YAm}，B={UB,WB,YBn} 。其中，UA和UB表示方向矩阵；WA和WB表示坐标矩阵。因UB和WB的表达方式分别与UA和WA类似，只给出UA和WA的表达式：

2 拼合算法

2.1 点云拼合的约束特征分析

点云的拼合需要将零件的几何特征进行对齐才能实现，首先需要确保约束特征达到拼合条件，使得用于拼合的几何特征是表达三维空间的唯一方式。零件特征可简化为平面、直线和点，即用这3种特征建立一个唯一的坐标系[14]。

由于特征没有方向的特性，难以用来直接表达坐标轴，因此可以通过5个元素（原点、x轴、x轴正方向、y轴、y轴正方向）来定义坐标轴，x轴和y轴只是通过同一个原点，没有方向，满足这5个元素的特征集则被认为是唯一的定义三维空间[15]。平面、直线和点可以组成多种特征集，如点集、直线集、平面集、平面-直线-点集等。通过分析知，点云的约束特征是否能拼合的判断方法是这些约束特征是否可以定义唯一的坐标系来表达三维空间，点云约束特征的数量与特征集拼合的可能性成正比。

2.2 计算思路

点云拼合的效果与拼合的适应度函数有关，当适应度函数达到最小值时，点云拼合效果最佳。拼合的适应度函数包含平面、直线与点拼合适应度3 种，平面和直线因为具有无限延伸、没有边界的特点，不能采用距离的方式定义其拼合适应度，而点拼合适应度则可以[16]。因此，针对特征拼合效果的评价有3 种方法，一是参数法，即评价平面方程参数、直线方程参数及点坐标参数的数值偏差，这种评价方式属于直接评价，参数偏差大小与点云的拼合效果成反比；二是距离法，即在一个包含所有点云数据的长方体空间内评价平面、直线及点的最大距离偏差，这种评价方法属于间接评价，计算相较第一种更复杂，但精度更高；三是组合法，即参数法与距离法的组合使用，结合了两种评价方式的优势。

2.3 计算步骤

粒子群算法是一种智能算法，通过群体中每个粒子位置和速度的不断更新进行迭代计算，来完成对问题寻优[17-18]。粒子群算法与遗传算法类似，但在解决一些典型函数优化问题时，优化结果会比遗传算法更佳[19-20]，可以简化问题解的编码与适应性函数的选择等步骤，简单易实现，且需要调整的参数较少，同时具有收敛速度快的优点，具备良好的应用前景。

粒子群算法计算步骤[21]如下。

（1）将旋转矩阵R与平移矩阵T组合作为粒子的位置参数，设置粒子群规模，并初始化粒子的位置和速度。

旋转矩阵R表示为：

平移矩阵T表示为：

（2）计算适应度函数f，并与定义的收敛值ζ进行比较。

（3）更新粒子的位置和速度并再次计算，直至f≤ζ为止。

（4）将旋转矩阵R与平移矩阵T用于点云YAM的坐标变换，最终实现与点云YBN的拼合。

2.4 参数法适应度函数

确定粒子群算法的变量为旋转矩阵R和平移矩阵T，根据特征参数的对应关系建立参数法适应度函数。

适应度函数为：

式中：fU为方向矩阵UA经旋转矩阵变换后与UB的误差；fW为坐标矩阵WA经坐标变换后与WB的误差；a为引入的平衡系数，用于平衡方向矩阵和坐标矩阵在元素数值大小方面的差距。

fU和fW的表达式为：

2.5 距离法适应度函数

确定一个长方体区域ϕ，使得点云YBN和经过坐标变换的点云YAM均包含在内：

计算集合B中的某一平面与ϕ的边线相交得到的交点，再计算几个交点到经过坐标变换后的集合A中对应平面的垂直距离，取最大值，即表示两平面在长方体区域ϕ内的最远距离偏差。用Γ表示ϕ的边线集，针对集合A和B的i平面计算拼合偏差值fMi：

用Ψ表示ϕ的边界平面集，针对集合A和B的j直线计算拼合偏差值fXj：

针对集合A和B的k点计算拼合偏差值fDk：

由此得到距离法适应度函数f：

3 实例分析

本文以发动机右半轴支架为例进行分析，两次测量得到的点云和特征数据如图1 所示。安装面、安装轴与定位孔是这个零件比较重要的特征，因此可以选取一个平面、一条直线、一个特征点来代表这个发动机右半轴支架点云拼合的约束特征。其中，平面表示安装面，直线表示安装轴，点表示支架上其中的一个定位孔。

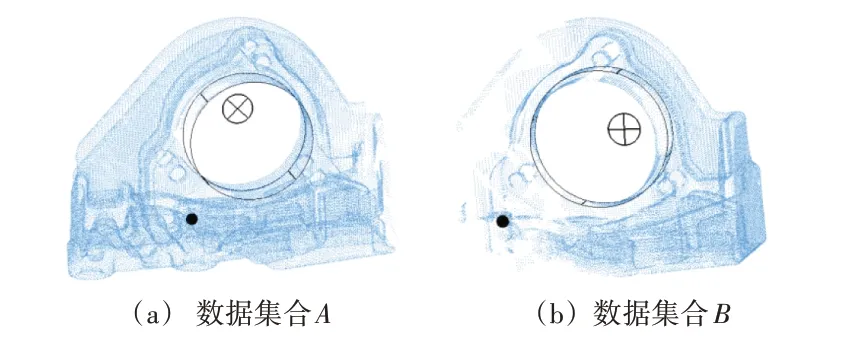
图1 测量数据

（1）设定适应度允许值为0.1，分别采用参数法与距离法进行计算及收敛性比较，结果如表1 所示。由表可知，参数法的收敛性很好，5 次计算均能够在10 s 内完成收敛；距离法的收敛效果很差，5 次计算仅有1 次完成收敛。

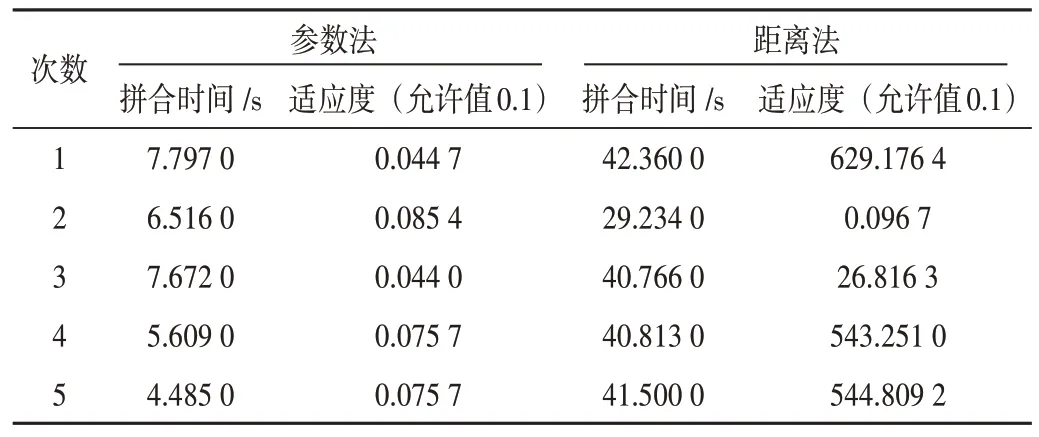
表1 参数法与距离法收敛性比较

（2）设定适应度允许值为0.01，分别采用参数法与组合法进行计算，其中组合法是进行两次粒子群计算，第1次采用参数法，第2次采用距离法，第1次的计算结果作为第2次计算的初始值。

比较参数法与组合法的收敛性结果如表2 所示。由表可知，两种方法的收敛速度相当，组合法的平均收敛速度略低。

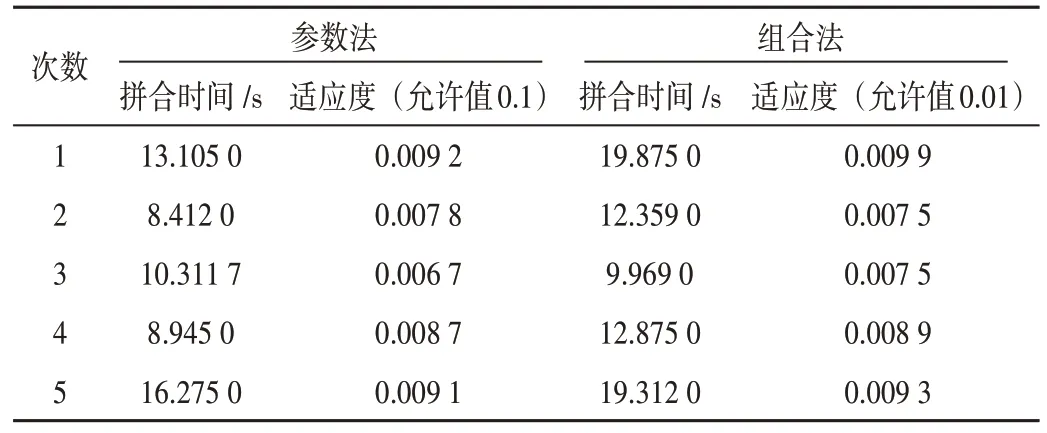
表2 参数法与组合法收敛性比较

比较参数法与组合法的拼合精度，选择拼合后点云的部分截线进行分析，参数法得到的拼合点云存在错缝，组合法得到的拼合点云重合度较好，如图2所示。

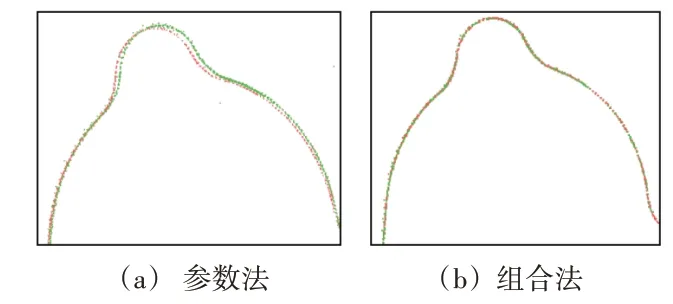
图2 拼合精度比较

采用组合法得到拼合点云如图3 所示，可很好地用于后期的三维模型重建工序。

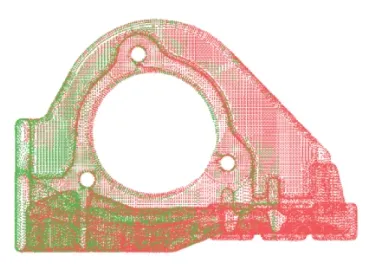
图3 组合法拼合的点云

4 结束语

本文基于粒子群算法，采用几种方法对点云特征进行拼合，结果表明：（1）参数法计算速度快，收敛性好，但整体精度不高；（2）距离法收敛性差，一旦收敛则具有较好的拼合精度；（3）组合法同时具备了参数法与距离法的优点，具有计算速度快，收敛性好，拼合精度高的特点。

本文以发动机右半轴支架为例进行点云拼合方法的研究，最终摸索出了基于零件原有平面、直线或点特征的一种点云拼合方法，通过粒子群算法进行参数法及距离法数学模型的计算，减轻复杂问题的计算负担；与原拼合方法相比，本文探索的拼合方法拼合速度更快、拼合精度更高，能够很好地用于点云数据处理，为后期三维模型重建打下坚实的基础。