不同冲刷及腐蚀环境下连续桥梁的概率地震需求分析

陈 刚，朱云会，陈小勇，李俊杰，何余良

1.绍兴市交通建设有限公司，浙江绍兴 312000

2.绍兴文理学院，浙江绍兴 312000

0 引言

国外的许多学者针对水流对桥梁的冲刷问题进行了相关研究，Smith［1］采用统计学方法对1784年至1975年全世界范围内典型的143座桥梁的破坏进行统计分析，其中由于水流冲刷造成的桥梁破坏多达70 座。Wardhana 等［2］利用数理统计学方法分析了1989年至2000年的500多座有关桥梁破坏案例，分析桥梁破坏原因时发现，洪水冲刷所占的比例最大。国内外有许多桥梁的破坏都与水流冲刷有关，如1987 年纽约Sehoharie Creek桥的倒塌，1989年俄亥俄州Miamstown便桥的倒塌，2009年黑龙江铁力桥垮塌事故，2010 年河南栾川汤伊运河大桥倒塌等［3］。

劳尔平等［4］采用二维平面建立水流数学模型来模拟建筑物周围的流场，研究水流在建筑物周围的冲刷深度变化，为研究水流冲刷深度公式提供了新的思路和方法。袁晓渊［5］建立不同的桥墩冲刷工况，归纳总结之前学者在二维平面中桥墩局部冲刷深度公式的方法和结论。

在冲刷深度公式研究方面，齐梅兰等［6］研究新型桥墩冲刷深度公式，对新型桥墩进行扩充试验，提出适合新型桥墩冲刷深度的理论公式。高徐昌［7］为了研究桥墩在潮流作用下局部冲刷和水流特性的变化规律，采用Fluent模型进行建模分析，利用桥墩局部冲刷试验数据和已有历史数据进行对比分析，拟合出桥墩在潮流冲刷下的局部冲刷深度公式。杨延凯等［8］建立了桥梁在冲刷和地震作用下的概率地震需求模型，研究桥梁的防灾体系并提出了基于地震风险思想的桥梁多灾害分析框架，此外，还提出并建立了桥梁在冲刷和地震共同影响下的组合计算方法，为继续研究桥梁在冲刷和地震作用下影响变化提供了新的途径和思路。

因桥梁下部的冲刷深度较难准确测量，张效忠等［9］提出一种适用桥墩冲刷深度的分析方法，采用先进的向量随机方法和特征算法对桥梁冲刷深度进行识别，此方法适用于桥梁在环境复杂条件下深度的测量，大大地提高了工作效率，减少了人力、物力及财力的投入，更重要的是提高了测量的准确度。

沿海桥梁在使用过程中，由于受水流冲刷和氯离子侵蚀等环境因素影响，桥梁中各种材料的性能会随着使用年限的增加而逐渐退化，抗震性能也随之降低。桥梁抗震设计时一般不考虑材料性能随使用年限增加而退化的问题，认为结构材料性能在运营期间不发生改变。相关资料显示，许多桥梁服役到一定时间，其结构材料的力学性能发生退化，根本达不到设计使用年限，桥梁在实际服役期间的平均使用寿命只有44年［10］。锈蚀因素对钢筋混凝土结构力学性能的影响主要表现在以下四个方面：第一，钢筋外部发生锈蚀，使得钢筋的有效截面积减小从而导致钢筋的力学性能逐渐下降［11］；第二，因钢筋发生锈胀，钢筋与混凝土之间会出现孔隙和裂缝，导致钢筋与混凝土之间的粘结作用逐渐降低［12］；第三，由于钢筋与混凝土之间的粘结作用下降，钢筋继续锈蚀膨胀时，之间的黏结作用力为零，导致钢筋外层的混凝土剥落［13］；第四，因钢筋发生锈胀，钢筋的截面积减小，钢筋与混凝土之间的握裹力下降，导致钢筋对核心混凝土的有效约束逐渐下降［14］。

Han等［15］研究冲刷作用对桥梁桩基的抗震性能变化规律，利用Pushover 方法对其进行模拟分析，结果表明冲刷使得桥梁基础所受土体的约束减小，结构的承载力下降。郑凯锋等［16］研究汶川地区简支梁桥的地震易损性，采用概率地震需求模型分析桥梁在地震作用下的抗震性能，得出了简支梁桥的抗震性能变化规律。周神根等［17］为了研究桥梁的抗震性能，较早地提出使用Pushover 分析法对其进行研究，并取得了不错的研究成果。本文尝试通过对某沿海桥梁（图1）在4种冲刷深度和4种腐蚀程度下进行纵横桥两个方向的Pushover 分析，研究桥梁在纵横桥方向上的概率地震需求分析。

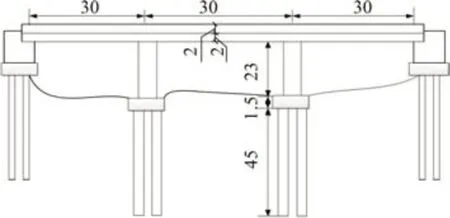
图1 某沿海桥梁

1 冲刷腐蚀桥梁Pushover分析

Pushover 分析方法常用于桥梁的抗震性能评估，是一种静力非线性的分析方法。本文采用静力加载方式进行逐级加载，牛顿迭代法进行分析计算，以及位移加载方式进行控制，每时间步位移增量为0.002 m，对桥梁进行500次水平推力分析，最大误差为1.0e-5，最大迭代数为5 000步，且边界约束采用OpenSees中的Transformation方法进行处理。

根据4种不同的冲刷深度和4种不同的腐蚀程度（表1），对全桥的纵横向进行Pushover分析，得出桥梁在4种不同冲刷深度下的纵横向Pushover曲线。

表1 腐蚀状态描述

1.1 各冲刷深度Pushover分析对比

当腐蚀程度一定时，桥梁在各种不同冲刷深度下纵横桥向的Pushover曲线见图2。

图2 不同冲刷深度下纵横桥的Pushover曲线

由图2可知，在纵横桥方向上，随着冲刷深度的增加，柱底剪力均逐渐减小。如零级腐蚀横向的水平位移为0.5 m时，随着冲刷深度的增加，其柱底剪力由9.987 2×107N分别减少到9.247 7×107、8.734 2×107、8.464 9×107N。由于水流冲刷作用，桩基础周围土体减少，暴露在外界环境中的桩体长度不断增加，结构在屈服状态时所受到的侧向抗力逐渐减少。在纵横桥方向上，桥墩的柱底剪力随着腐蚀程度的增加而逐渐降低，其原因是随着腐蚀程度的增加，墩柱的抗弯承载力逐渐降低，结构的侧向抗力也在逐渐减小。

1.2 各腐蚀程度Pushover分析对比

当冲刷深度一定时，桥梁在各种不同腐蚀程度下纵横桥的Pushover曲线见图3。

图3 不同腐蚀程度下纵横桥的Pushover曲线

由图3可知，零级腐蚀时，桥墩柱底剪力随着顶点位移的增加而逐渐增加，且冲刷为0 m时的剪力最大，其次是2、4 m，6 m冲刷时其剪力最小。当墩顶位移一定时，纵桥方向的柱底剪力大于横桥方向的柱底剪力，在一级腐蚀时，纵桥和横桥方向且墩顶位移为0.5 m时，剪力分别为9.473 2×106、8.867 7×106N。由图3 还可以发现，当桥梁发生一级腐蚀、二级腐蚀、三级腐蚀时，柱底剪力先增加然后逐渐下降，二级腐蚀时下降得较为明显，一级腐蚀和三级腐蚀影响不明显。在纵横桥方向上，随着腐蚀程度的增加，其结构的承载能力逐渐下降，墩底的柱底剪力逐渐降低。

2 概率地震需求模型的建立及分析

2.1 概率地震需求模型基本原理

首先选取合适的地震波并确定相关地震参数，之后对桥梁进行非线性时程分析，在选择地震波和确定地震需求参数后，对该桥的有限元模型进行了分析，得到地震动参数（im）与地震动需求参数（EDP）之间的关系［18］。本文假定桥梁结构服从正态分布，（EDP）样本与地震动参数（im）之间的关系满足公式（1）：

在本文中，假设地震需求参数的均值k和地震动峰值加速度PGA服从以下关系：

本文中结构的概率地震需求模型：

μ的统计参数为：

式（3）中的系数a和b是通过结构响应的统计分析和回归分析得到的。本文采用时程分析方法，对冲刷腐蚀桥梁在4种冲刷深度和4种腐蚀程度下的40条地震记录进行了分析。以峰值加速度PGA为自变量，对桥梁结构的地震响应数据进行回归分析，得到桥梁纵横向的概率地震需求模型。

2.2 各冲刷深度及腐蚀情况概率地震需求模型

1）冲刷深度为0 m，不同腐蚀情况下的概率需求模型以峰值加速度PGA为变量进行线性回归分析，4种腐蚀状态下纵横桥方向上的概率需求模型示意图见图4，线性回归函数见表2。

表2 冲刷深度0 m时不同腐蚀程度下概率需求模型

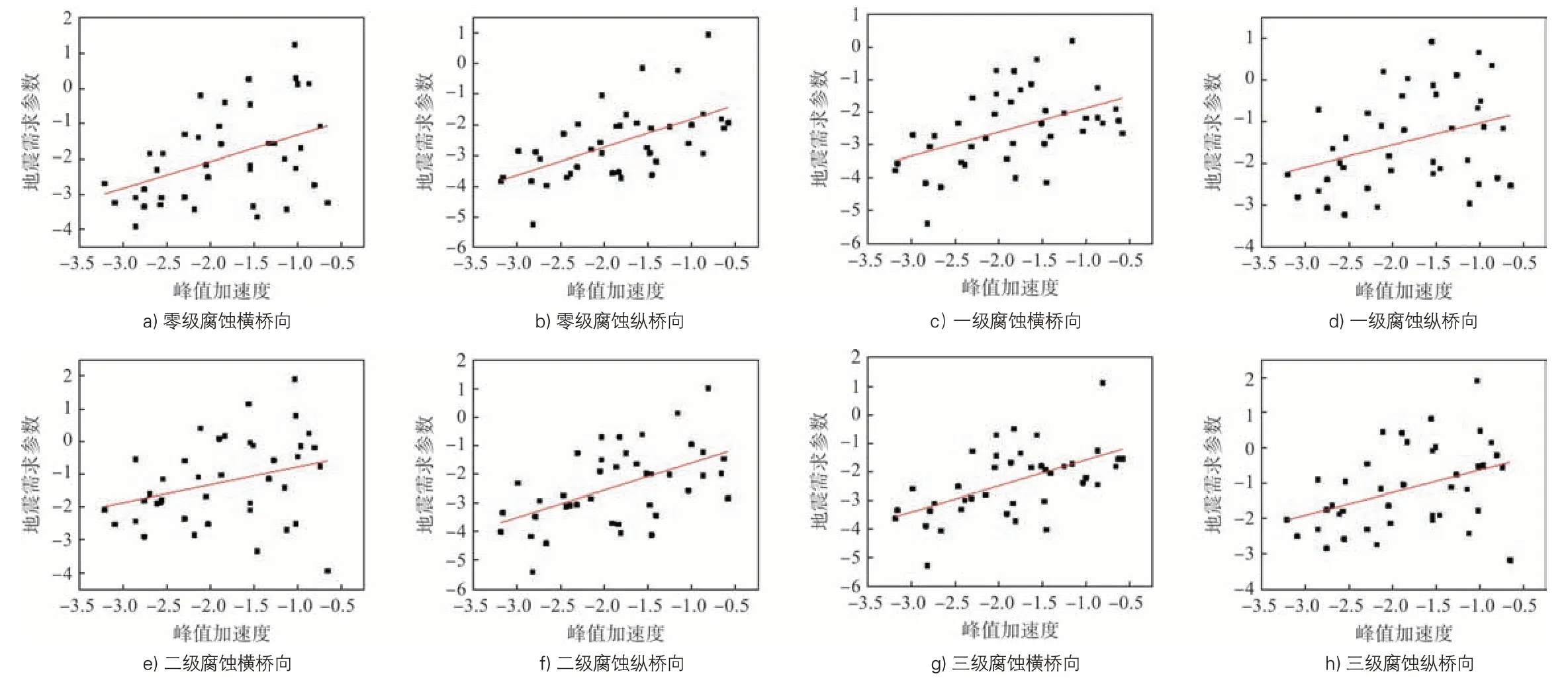
图4 冲刷深度0 m时不同腐蚀程度下概率地震需求

对比图4和表2可以发现，由横桥上和纵桥上的线性回归参数可知，横桥向和纵桥向的离散性较为接近，腐蚀因素对桥梁结构的影响较小。

2）冲刷深度为2 m，不同腐蚀情况下的概率需求模型以峰值加速度PGA为变量进行线性回归分析，4种腐蚀状态下纵横桥方向上的概率需求模型示意图见图5，线性回归函数见表3。

表3 冲刷深度2 m时不同腐蚀程度下概率需求模型

图5 冲刷深度2 m时不同腐蚀程度下概率地震需求

对比图5和表3可以发现，横桥方向上和纵桥方向上在一级腐蚀、二级腐蚀、三级腐蚀上线性回归方程的相关系数较为接近；横桥向和纵桥向的离散性较为接近。

3）冲刷深度为4 m，不同腐蚀情况下的概率需求模型以峰值加速度PGA为变量进行线性回归分析，4种腐蚀状态下纵横桥方向上的概率需求模型示意图见图6，线性回归函数见表4。

表4 冲刷深度为4 m时不同腐蚀程度下概率需求模型

图6 冲刷深度4 m时不同腐蚀程度下概率地震需求

对比图6和表4可以发现，横桥方向上在零级腐蚀、一级腐蚀、二级腐蚀、三级腐蚀上线性回归方程的相关系数较为接近；在地震强度作用下，腐蚀因素对桥梁的影响较小。

4）冲刷深度为6 m，不同腐蚀情况下的概率需求模型以峰值加速度PGA为变量进行线性回归分析，4种腐蚀状态下纵横桥方向上的概率需求模型示意图见图7，线性回归函数见表5。

表5 冲刷深度为6 m时不同腐蚀程度下概率需求模型

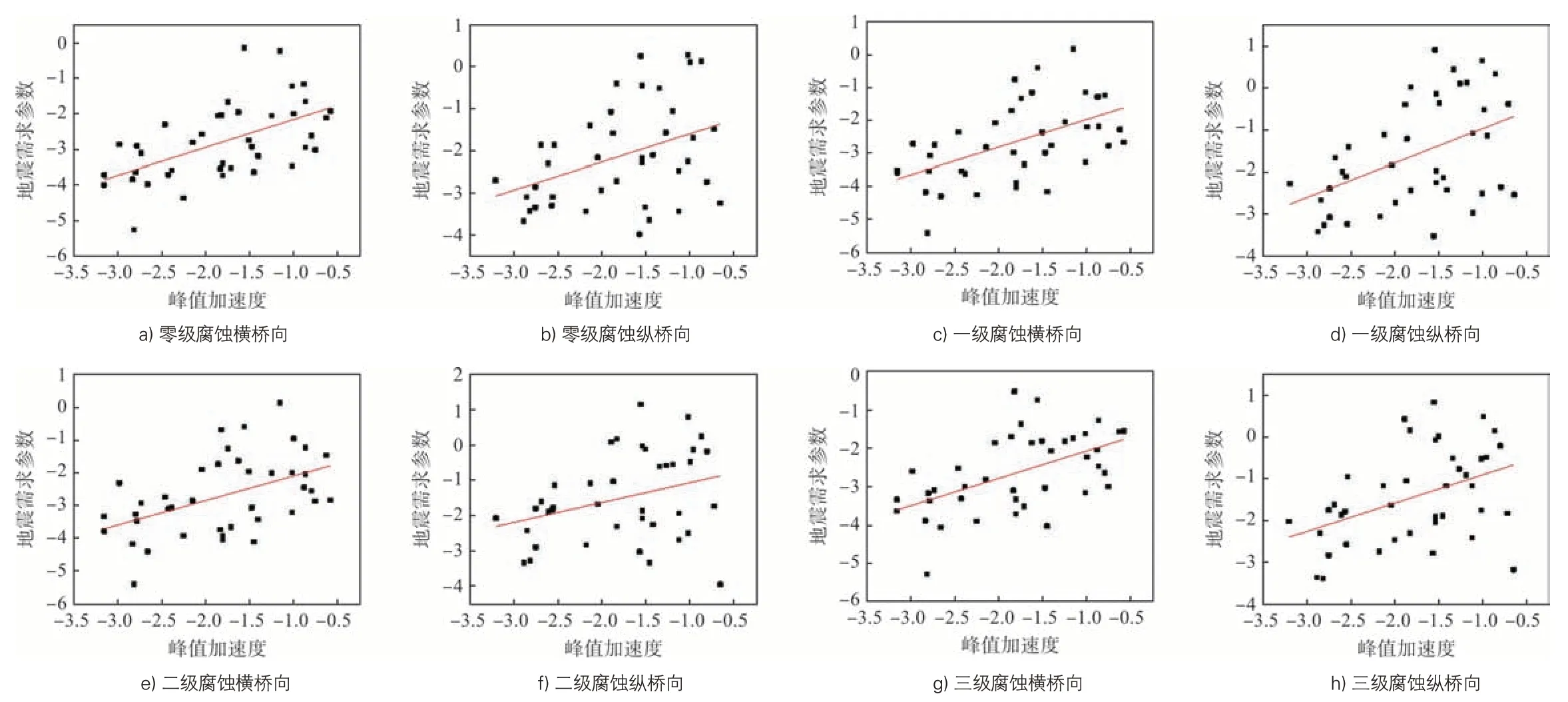
图7 冲刷深度6 m时不同腐蚀程度下概率地震需求

对比图7和表5可以发现，横桥方向上在一级腐蚀、二级腐蚀、三级腐蚀上线性回归方程的相关系数较为接近；在纵桥方向上，线性相关参数有差异；在地震强度作用下，纵桥的影响大于横桥的影响。

3 结论

考虑地震动的不确定性，对桥梁在不同冲刷深度和腐蚀程度下进行纵横桥方向的Pushover 分析和概率地震需求分析，得出以下结论：

1）对桥梁在4种冲刷深度和4种腐蚀程度下进行纵横桥两个方向的Pushover分析，结果表明：冲刷和腐蚀都会对桥梁的柱底剪力产生影响，且冲刷的影响更大；在纵横桥方向上，柱底剪力均随着冲刷深度的增加而逐渐减小。因为随着冲刷深度的增加，桩基础周围土体逐渐减少，裸露外界环境的桩体长度逐渐增加，导致结构的侧向抗力减少，桩的顶点位移逐渐增大；在纵横桥方向上，桥墩的柱底剪力都随着腐蚀程度的增加而逐渐降低，随着腐蚀程度的增加，墩柱的抗弯承载力逐渐降低，结构的侧向抗力也在逐渐减小。在纵横桥方向上，相同顶点位移所对应的柱底剪力，纵向大于横向，表明桥梁的纵向延性大于横向延性。

2）桥梁在4种冲刷深度与4种腐蚀程度横桥和纵桥方向上进行概率地震需求分析，并对地震参数和地震强度进行线性回归分析，得到桥梁在4种冲刷深度和4种腐蚀程度下纵横桥方向上的概率地震需求模型。

3）通过对比在纵横桥上的线性回归参数可知，横桥向和纵桥向的离散性较为接近。