基于分解法与轨迹搜索的无人机群轨迹多目标优化模型

柳隽琰，江沸菠*，彭于波，董莉

基于分解法与轨迹搜索的无人机群轨迹多目标优化模型

柳隽琰1，江沸菠1*，彭于波1，董莉2

（1.湖南师范大学 信息科学与工程学院，长沙 410081； 2.湖南工商大学 计算机学院，长沙 410205）（∗通信作者电子邮箱jiangfb@hunnu.edu.cn）

基于深度学习（DL）的传统多目标求解器存在模型利用率低以及容易陷入局部最优的问题。针对这些问题，提出了基于分解法与轨迹搜索的无人机群轨迹多目标优化模型（DTMO-UT）。所提模型包含编码与解码部分。首先，编码部分由设备编码器（Dencoder）和权重编码器（Wencoder）组成，用于提取物联网（IoT）设备的状态信息与权重向量的特征，其中权重向量代表分解多目标优化问题（MOP）的标量优化子问题，因此解决所有子问题即可解决该MOP。权重编码器可以实现对所有子问题的编码，从而提高了模型的利用率。然后，使用包含轨迹解码器（Tdecoder）的解码部分对编码特征进行解码，以生成帕累托最优解。最后，为了减少贪婪策略陷入局部最优的现象，为轨迹解码器设计轨迹搜索技术，即通过生成多个候选轨迹选标量值最优的轨迹作为帕累托最优解，从而增强了轨迹解码器在轨迹规划时的探索能力，并获得质量更好的帕累托集。仿真实验结果表明，所提模型相较于主流的基于DL的MOP求解器，在模型参数量降低98.93%的情况下，MOP解的分布性提高了0.076%，延展性提高了0.014%，平均综合性提高了1.23%，表现出较强的实用性路径规划能力。

轨迹规划；深度学习；多目标优化；分解法；帕累托集

0 引言

物联网（Internet of Things， IoT）技术的快速发展提高了诸多时延敏感型应用的服务质量（Quality of Service， QoS），例如智能交通［1］、智能辅助医疗［2］和应急救援［3］等。在这些应用中，被采集的信息需要尽快传输到中心服务器进行分析与决策，过时信息可能导致严重的控制错误或安全事故；因此，保证信息的新鲜度非常重要［4］，衡量信息新鲜度的指标为信息年龄（Age of Information， AoI）。数据收集系统中AoI的优化也在近几年受到了广泛关注［5］。无人机（Unmanned Aerial Vehicle， UAV）具有强大的机动性与灵活性，适合在数据收集系统中作为数据采集器［6］。一架UAV能按设定的轨迹依次采集沿线所有物联网设备（IoT Device， IoTD）的数据再返回数据中心，以实现高效化的数据收集；但相较于无人车和基站，UAV更易受到自身数据存储和电池容量的限制，所以在UAV辅助数据收集系统的设计中，通常需要考虑UAV的数据存储约束与能耗优化，而能耗与AoI存在的竞争关系会导致二者难以同时最小化［7］。如果降低系统能耗，那么被采集数据的AoI就会延长；同理，若缩短AoI，系统总能耗则会增加，因此，该优化问题是一个典型的多目标优化问题（Multi-objective Optimization Problem， MOP）［8］。在轨迹规划过程中，多目标规划存在多个需要优化的目标，且这些目标之间通常是互相竞争的关系。MOP的目的是同时极大化或极小化多个具有冲突性或矛盾性的目标的最优化问题［9］；而解决MOP不同于解决经典的单目标优化问题，它的解并非唯一，即不存在一个最优解，因此传统的单目标优化器［10］难以解决MOP［9］。所以只能通过在多个目标的优化中进行协调［7， 11］得到一组折中解以解决MOP，其中折中解也被称为帕累托最优解，这组折中解的集合被称为帕累托集。对于本文研究的场景，帕累托最优解是不被帕累托支配UAV轨迹，即如果一个UAV轨迹的能耗与AoI不能被其他任何UAV轨迹全面超越，那么该轨迹是一个帕累托最优解。

求解帕累托集的方法有精确法与近似法。由于帕累托集中解的数量庞大，且每个帕累托最优解的求解难度随着问题规模呈指数级上升，所以用精确法求解大规模的多目标优化问题是不实用的［12］，因此，在合理时间内找到接近最优解的近似法成为更实用的方法。其中：Srinivas等［13］提出了NSGA（Non-dominated Sorting Genetic Algorithm），通过生成数量庞大的解并筛选非支配解求出不被支配的帕累托最优解；Deb等［14］在NSGA中引入了精英策略并得到了著名的二代NSGA（NSGA-Ⅱ），大幅提高了运算效率；Bozorgchenani等［7］采用NSGA对移动边缘计算系统中的能耗与处理延迟进行优化；Ghambari等［15］改进了NSGA以优化UAV轨迹规划中的能耗与效率。NSGA可以快速、直观地得到帕累托集；然而，需要考虑多目标的适应度分配与解的多样化维护，需要大量的专家知识从而难以执行［16］，因此，复杂度更低且更容易实现的分解法成为了解决多目标优化问题的主流方法［9］。该方法把MOP分解为若干标量优化子问题，每个子问题采用一个权重向量聚合多个目标值从而得到一个标量值，目的是最小化该标量值。每个子问题的最优解都是帕累托最优解［16］，因此解决所有子问题即可求得整个帕累托集。在基于分解法的传统方法中，启发式搜索算法是主流：Zhang等［16］结合分解法与进化算法，并采用近邻策略优化种群，提出了MOEA/D（Multiple Objective Evolutionary Algorithm based on Decomposition）；周爱民等［17］在MOEA/D的基础上采用了一个改进的混合高斯模型对群体建模并采样产生新个体，并利用贪婪策略更新群体，从而求解整个帕累托集；侯薇等［18］采用混合交叉策略充分利用不同交叉算子的优势，同时针对演化过程收敛的特点与结合局部搜索策略求解帕累托集。在分解法的基础上采用经典单目标优化方法也能够解决子问题，其中较著名的工具为谷歌团队研发的OR-Tools（Operations Research-Tools）［19］，OR-Tools整合并改进了诸多经典优化器，如Concorde［20］、Gurobi［21］等，并在实际使用时根据问题规模与数据特点进行自适应选择。相较于帕累托占优的方法，基于分解法的方法具有更低的复杂度且更容易实现［16］

在基于深度学习（Deep Learning， DL）的优化方法中，已经有诸多解决单目标优化问题的研究，如循环神经网络（Recurrent Neural Network， RNN）［22］、指针网络（Pointer Network， PN）［23］和注意力模型（Attention Model， AM）［24］等。相较于启发式搜索算法，基于DL的方法运算速度大幅提升，且整体性能已经接近甚至超越启发式搜索算法。在DL解决MOP的研究中，Li等［25］采用分解法与PN模型对每个子问题进行求解，并训练了多组模型适应不同的权重向量；Wu等［26］采用分解法与AM求解所有子问题，并采用联合优化策略让权重向量接近的模型联合解决子问题；Zhang等［27］采用进化算法对AM的所有子问题的解二次优化，并用优化后的结果调优模型，同时解决了多目标优化中带时间窗的问题；董健等［28］提出了基于全连接神经网络的天线结构多目标设计方法，并采用多目标离子群算法对网络进行优化；黄博南等［29］采用若干RNN作为子问题的求解器解决综合能源系统的污染物排放量和综合运行成本。然而，这些方法需要训练多个模型以适应权重向量不同的子问题，因此模型利用率低［9］；同时，DL方法在输出轨迹时通常采用贪婪策略输出所有访问节点，容易陷入局部最优［30］。

本文的主要工作如下：

1）首先将UAV辅助的数据收集系统中能耗与AoI的优化建模为一个MOP，通过求解帕累托集解决该MOP。为此，采用分解法把MOP转换为多个标量优化子问题，每个子问题都是通过优化UAV轨迹最小化一个标量目标值，解决所有子问题可得到帕累托集，即优化能耗与AoI的折中方案下中所有最优UAV轨迹；同时，提出了高性能的DTMO-UT模型解决所有子问题，从而得到高质量的帕累托集。

2）在DTMO-UT模型的编码器部分，提出了设备编码器（Device encoder， Dencoder）与权重编码器（Weight encoder， Wencoder）分别提取IoTD状态信息与权重向量的特征，其中IoTD状态信息包含该IoTD的位置与带传输数据量。采用Dencoder与Wencoder即可编码所有标量优化子问题的特征，实现用一个模型解得整个帕累托集，提高了模型的参数利用率。

3）在轨迹解码器（Trajectory decoder， Tdecoder）中加入轨迹搜索。在解决子问题时，Tdecoder首先输出多个IoTD均不相同的初始访问候选轨迹，之后选择标量值最优的候选轨迹作为帕累托最优解。轨迹搜索增强了Tdecoder的全局搜索能力，能够得到质量更好的帕累托集。

1 系统模型与优化问题

1.1　系统建模

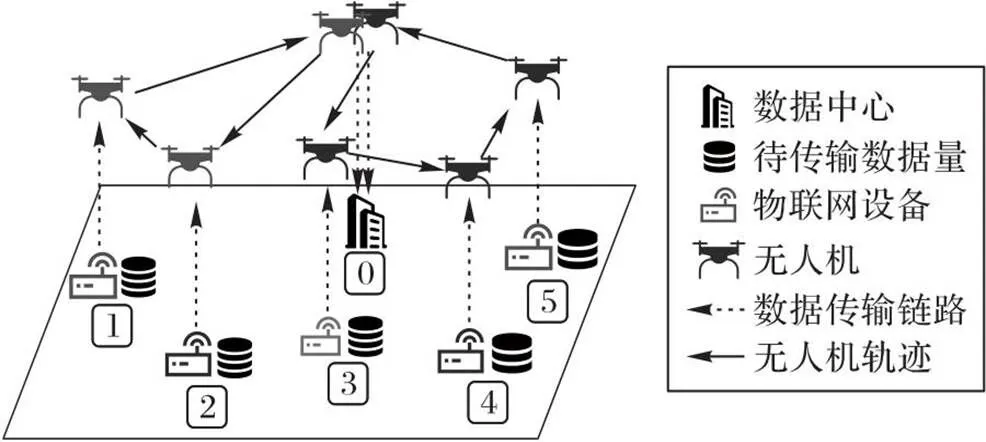
图1　多UAV辅助的数据收集系统

1.2　数据收集模型

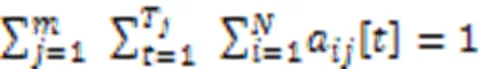
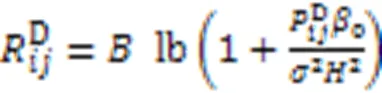
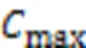
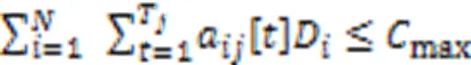
1.3　路径规划模型

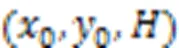
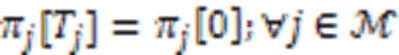
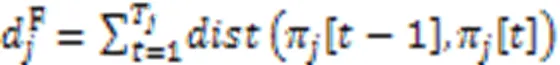
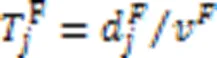
1.4　UAV能耗模型

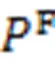
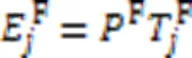
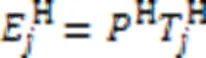
传输（T表示传输（Transfering））能耗为：

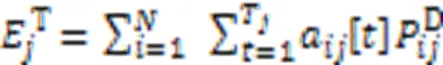
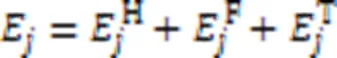
1.5　信息年龄模型

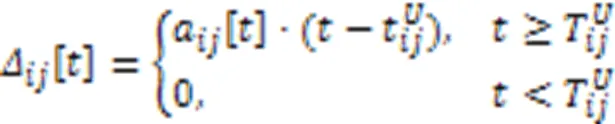
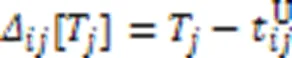
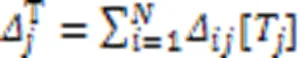
1.6　问题定义

在本文系统，有两个优化目标：一是最小化能耗，二是最小化采集数据的AoI。系统能耗的定义为：

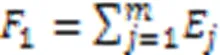
系统的AoI定义为所有UAV的最大AoI：

所以，本文的优化目标为：

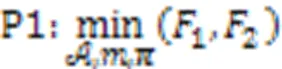
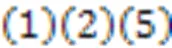
1.7　问题分析

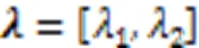
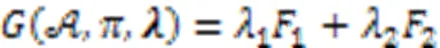
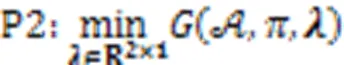
2 本文模型

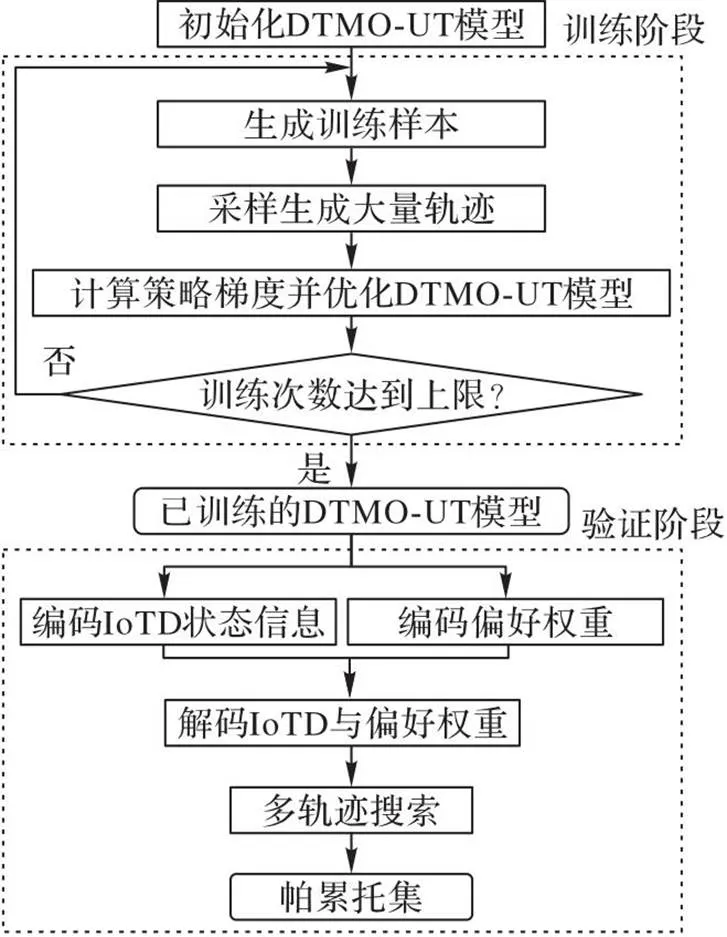
图2　DTMO-UT模型的训练与验证流程

为了得到高性能的DTMO-UT模型，训练阶段需要产生大量训练数据，其中一个训练数据包含随机分布的IoTD、不同的待传输数据量和一个对应偏好权重。之后DTMO-UT针对每个训练数据采样大量轨迹用于计算策略梯度从而优化DTMO-UT模型。当达到最大训练次数后即可完成训练。在验证阶段，DTMO-UT的Dencoder与Wencoder分别对IoTD状态信息与权重向量进行编码以提取特征，之后在Tdecoder中解码并生成解，轨迹搜索通过生成多个轨迹并择优的方式能帮助Tdecoder减轻局部最优并找到更好的解，当所有标量优化子问题解决后即可得到帕累托集。DTMO-UT模型实现了高参数利用率并能得到高质量帕累托集。所有帕累托最优解在多目标空间的映射称为帕累托前沿，也能体现多目标优化算法的综合性能，本文研究的多目标为能耗与AoI，因此每个帕累托最优解映射为一个点。当帕累托前沿越接近“左下”时，帕累托集的质量越高。得到帕累托前沿的过程如图3所示。

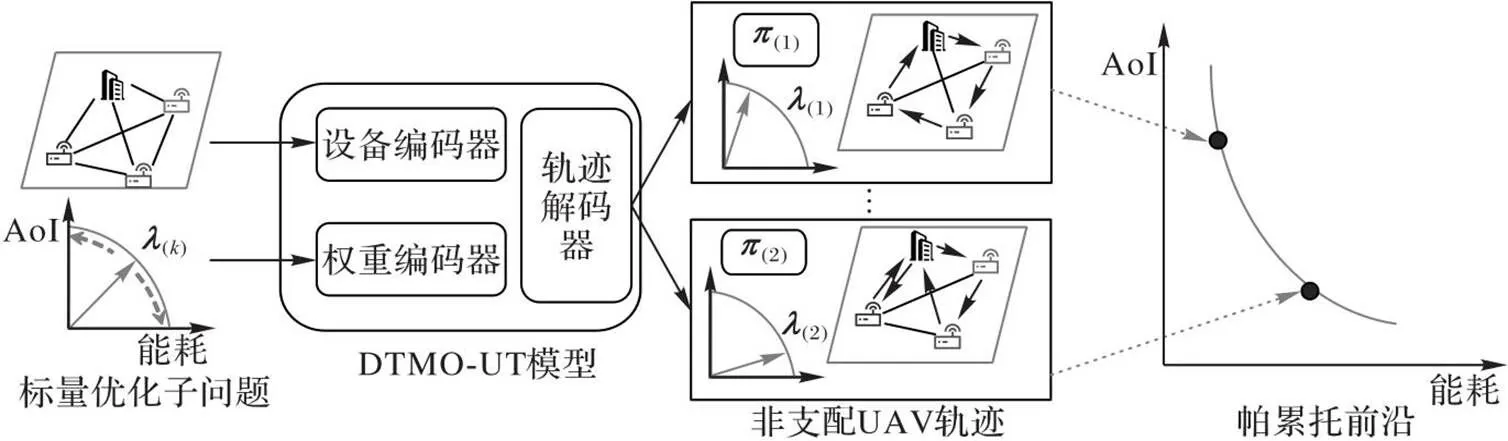
图3　DTMO-UT模型得到帕累托前沿的过程

在处理MOP时，本文采用在MOEA/D的分解法把能耗与AoI优化问题分解为若干标量优化子问题，并采用一组权重向量表示所有子问题。不过在解决子问题时，本文采用基于DL的DTMO-UT模型提取IoTD信息与权重向量的特征并生成对应的帕累托最优解，而非MOEA/D的启发式搜索；其次，DTMO-UT模型支持输入实数范围内的权重向量，因此能解决的子问题数为无穷，而MOEA/D仅能处理固定数量的子问题。

2.1　DTMO-UT模型

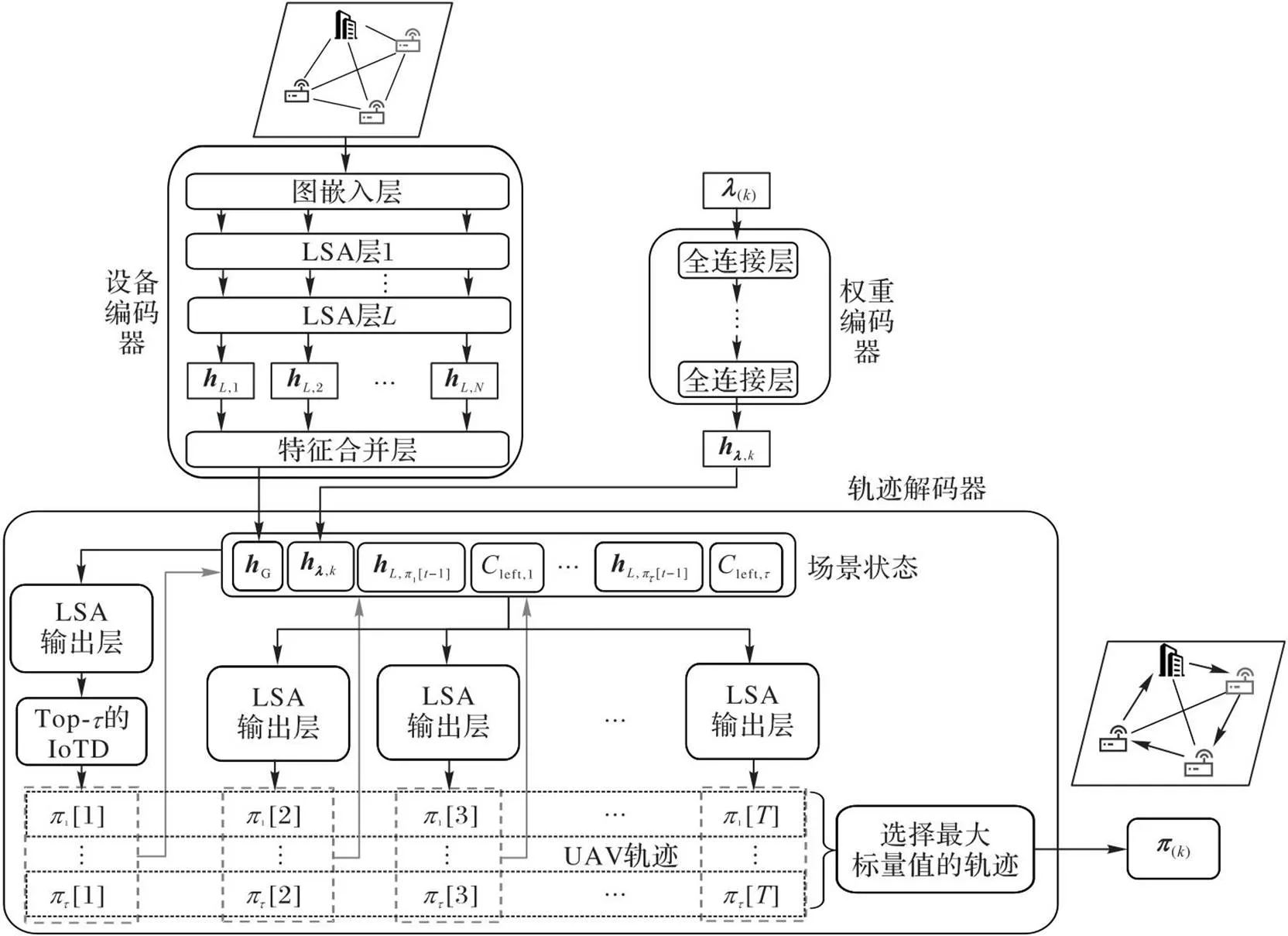
图4　DTMO-UT模型的结构

2.2　设备编码器

Dencoder主要用于提取IoTD状态信息。场景中的IoTD以图的形式进行存储，包含节点信息与边信息。Dencoder包含3个部分：图嵌入层、LSA层和特征合并层。

2.2.1图嵌入层

本文提出了基于图嵌入与LSA机制的Dencoder对IoTD状态信息编码。图嵌入可以有效提取IoTD的图信息，因此本文采用了基于Structure2Vector（S2V）［31］结构实现图嵌入层。注意力机制可以使模型注意重要的特征信息，并通过加权的方式体现关注程度［32］，LSA机制则可以让模型对输入的信息自发地产生不同的关注，从而提取IoTD自注意力特征以产生当前权重向量下的一组帕累托最优UAV轨迹。最后通过一个特征合并层合并所有IoTD自注意力为一个全局图特征。

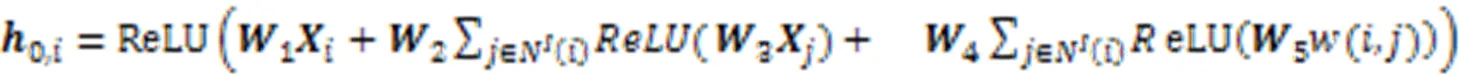
2.2.2线性自注意力层

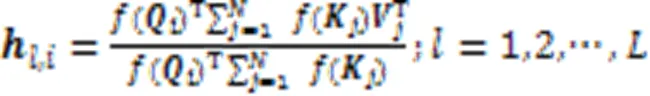
2.2.3特征合并层

在得到IoTD的自注意力特征后，对IoTD的自注意力特征进行合并。在合并特征时，文献［24］中对LSA特征以求平均值的方式进行合并；虽然平均值法非常高效，但是容易导致特征不可恢复的缺失［37］。所以本文采用一个可学习的线性特征合并层合并所有IoTD的自注意力特征得到全局图特征，公式为：

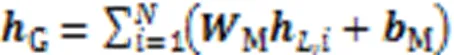
2.3　权重编码器

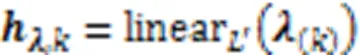
2.4　轨迹解码器

2.4.1轨迹搜索下的场景状态

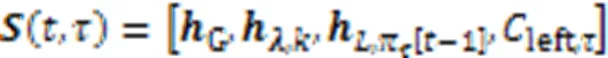
2.4.2线性自注意力输出层

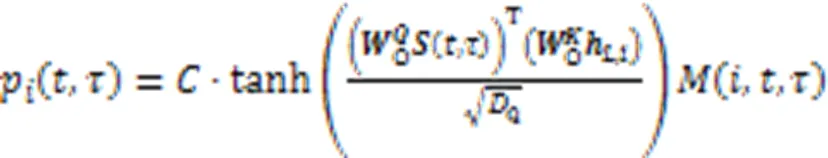
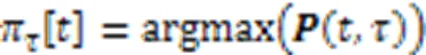
2.5　多目标REINFORCE训练算法

为了在无标签数据下训练得到高性能DTMO-UT模型，本节将介绍针对MOP的DL训练方法。因此，状态、行为和奖励如下。

状态 在每一步的轨迹规划中，输入的状态为：

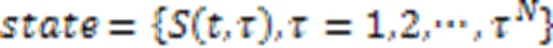
行为 DTMO-UT模型的行为是让UAV选择一个IoTD进行数据收集或者回到数据中心：

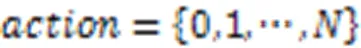
奖励 奖励为能耗与AoI与权重向量的加权和的负数：

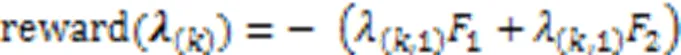
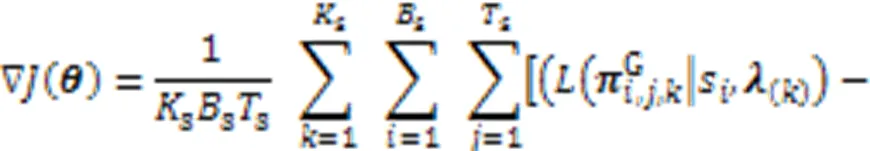
3 实验与结果分析

3.1　参数设定

本文将设计DL模型的参数对比、与主流方法的综合性能的对比实验验证DTMO-UT模型的高效性。此外，为了使模型收敛，本文的训练采用的学习率为0.001，学习率衰减（learning rate decay）为0.96，训练迭代次数为200［9］。运行环境配置是Windows 11操作系统，PyTorch 1.7.1框架，显卡为NVIDIA RTX3060，处理器为i7-11500与16 GB内存。

3.2　模型参数对比

首先，本文将DTMO-UT模型与同样基于分解法和AM的MODRL/D-AM（Multiple Objective Deep Reinforcement Learning using Attention Model）［26］模型的参数量与可解决的子问题数量进行对比，其中D（Decomposition）是多目标优化中常用的分解法。MODRL/D-AM把多目标问题分解为101个［9，16，39］标量优化子问题。因此，对比结果展示在表1中。

表1参数量与可解决的子问题数的对比

Tab.1　Comparison of parameter quantities and solvable sub-problems

在许多基于分解法的DL方法中，分解的子问题数为101［25-27］，在MODRL/D-AM中，由于需要针对每个子问题专门优化参数，因此总体参数量远超DTMO-UT模型。DTMO-UT模型的参数量相较于MODRL/D-AM减少了98.93%，且MODRL/D-AM只支持有限个标量子问题的权重向量；而DTMO-UT模型的Wencoder支持输入实数范围内的权重向量，因此可以解决数量不固定的子问题。从表1可以看出DTMO-UT模型具有更少的参数使用量，并支持灵活数量的权重向量。

3.3　总体性能对比

为了检验DTMO-UT模型的总体性能，本文采用对比帕累托前沿的方式，帕累托前沿是所有帕累托最优解在多目标解空间的映射，因为每个解有能耗与AoI两个指标，因此可以映射到一个二维平面。在对比算法中，除了上一小节提到的MODRL/D-AM，还有OR-Tools［19］、NSGA-Ⅱ［14］、MOEA/D［16］和未采用轨迹搜索的DTMO-UT（DTMO-UT model with No trajectory search， DTMO-UTN）模型。参数设定为：

1）MOEA/D。分解的子问题数为100，邻向量数为10，种群数为100，个体长度为150，单点交叉算子概率为0.9，变异算子概率为0.01，迭代次数为150。

2）NSGA-Ⅱ。种群数为2 000，个体长度为150，交叉算子概率为0.9，变异算子概率为0.01，迭代次数为25 000。

3）OR-Tools。子问题数为101，并采用加权求和的方式定义所有子问题。

4）MODRL/D-AM。分解的子问题数为100，隐藏层维度为128，训练数据批大小为200，数据量总大小为500 000。

由图5可得，所有方法得到的帕累托前沿均为凹状，其中DTMO-UT与MODRL/D-AM的曲线是接近的，因为这两个方法所提出的模型都是基于AM且采用深度强化学习进行训练，而它们均优于NSGA-Ⅱ、MOEA/D与OR-Tools。

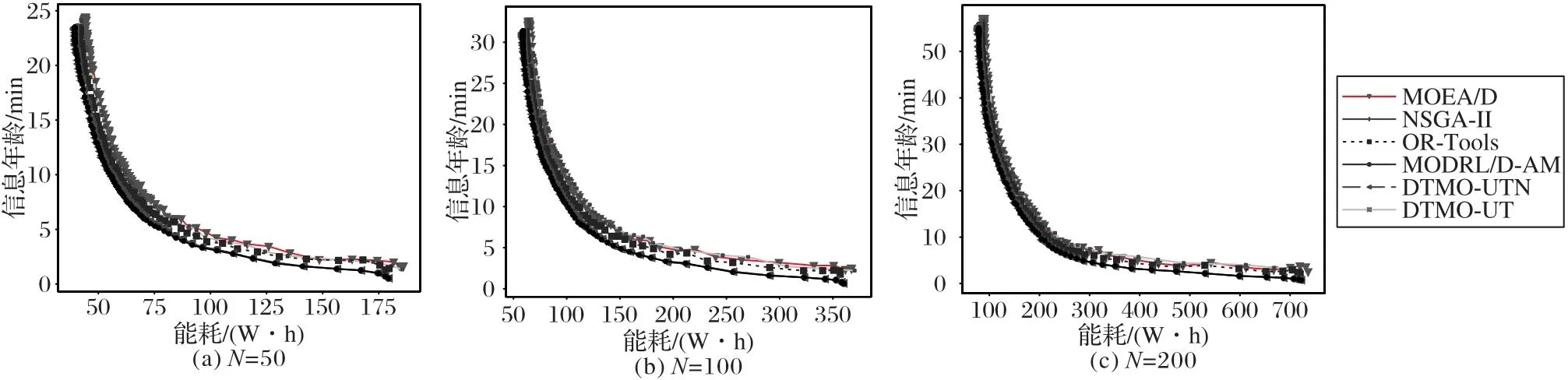
图5　不同场景下所有方法所得到的帕累托前沿对比

表2分布性与延展性指标的对比

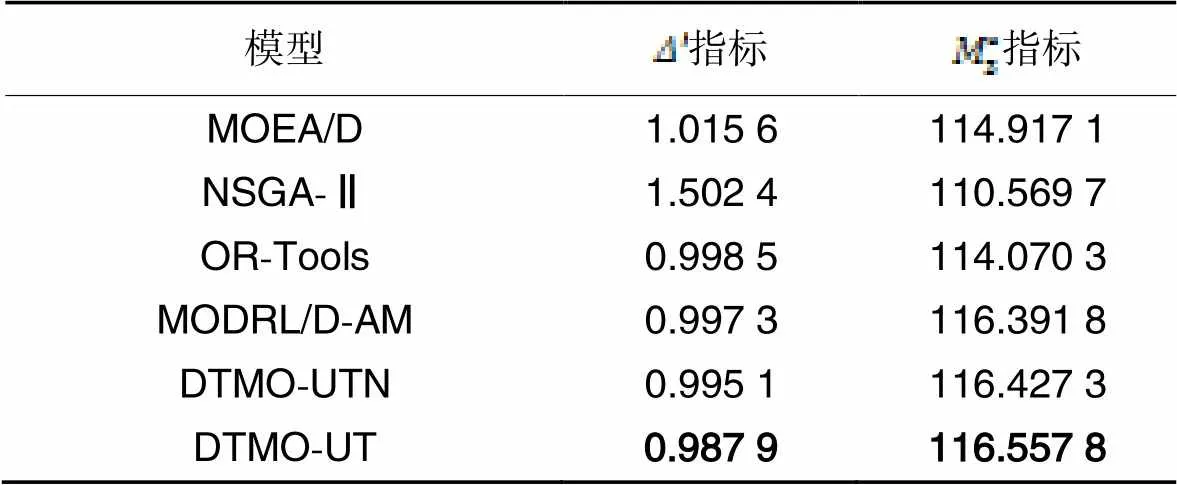
Tab.2　Comparison of distribution and ductility indicators

从表2中可以总结出DTMO-UT模型在分布性与延展性都优于其他方法，是因为：1）分解法更容易得到均匀的解集，2）DTMO-UT模型的轨迹搜索能提升每个子问题的解的质量，因此提高了解极端值的能力。在启发式方法中，NSGA-Ⅱ并非基于分解法，因此容易产生不均匀的解集，所以MOEA/D能得到比NSGA-Ⅱ更好的解集。

从表3可以总结出基于DRL的DTMO-UT、DTMO-UTN与MODRL/D-AM在所有测试数据中的性能以及运算时间均优于基于启发式搜索的NSGA-Ⅱ、MOEA/D与OR-Tools。

在运算时间的对比中，MODRL/D-AM优于DTMO-UTN与DTMO-UT，并远少于NSGA-Ⅱ、MOEA/D与OR-Tools，原因是：1）谷歌团队对OR-Tools的优化器进行了优化，从而比NSGA-Ⅱ、MOEA/D运算更快。2）基于DL的方法无须反复迭代且有并行计算的加持，使运算速度远超NSGA-Ⅱ与MOEA/D。3）MODRL/D-AM仅设计一个编码器用于编码IoTD信息，其模型结构比DTMO-UT简单，因此MODRL/D-AM运算速度较快。4）DTMO-UT的轨迹搜索会生成若干候选轨迹，因此DTMO-UTN运算比DTMO-UT更快。但是表1与表3所示MODRL/D-AM需要占用更多存储空间且性能不及DTMO-UT，采用轨迹搜索后DTMO-UT的运算效率并未损失太多同时性能上有提升。

在性能对比中，对于所有HV值的指标，DTMO-UT最高，DTMO-UTN与MODRL/D-AM次之，之后是OR-Tools、MOEA/D与NSGA-Ⅱ，原因是：1）DRL方法训练的模型具有更好的泛化能力。2）自注意力模型比启发式搜索算法具有更强的特征提取能力。3）采用了轨迹搜索的DTMO-UT模型能够减轻局部最优的现象，得到更高质量的帕累托集，从而提高了HV值，并降低了多次测试结果的标准差。

表3HV值的最大值、最小值、平均值、标准差以及算法运算时间的对比

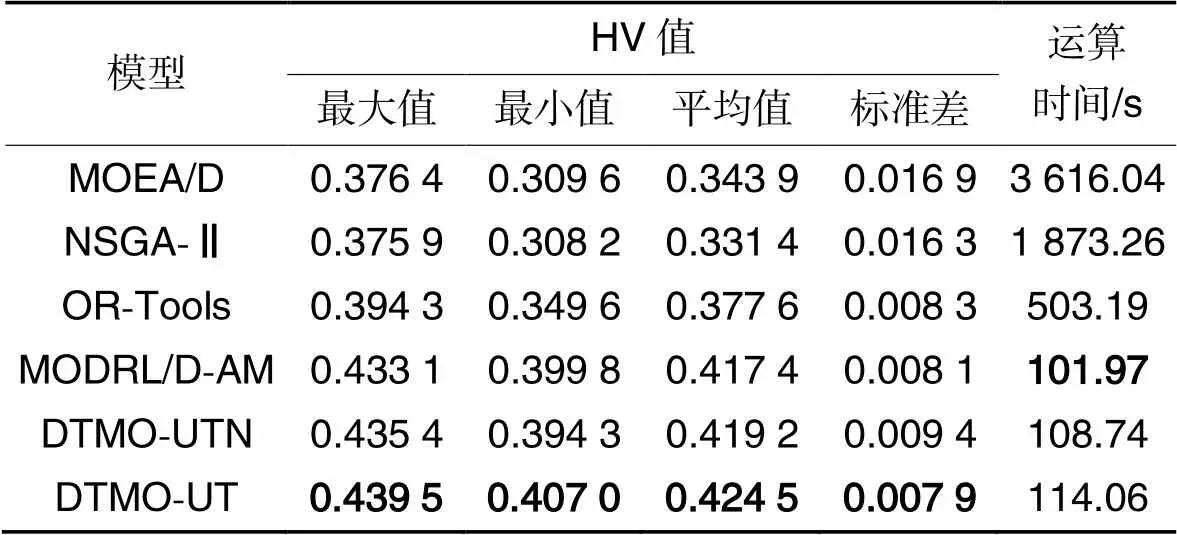
Tab.3　Comparison of maximum， minimum， average and standard deviation of HV value as well as algorithm running time

4 结语

本文研究的是一个通过优化UAV轨迹最小化数据收集系统中的能耗与AoI的MOP，通过求出帕累托集解决该MOP。考虑到求解帕累托集的传统方法存在模型利用率低和容易陷入局部最优的问题，本文在分解法的基础上提出了DTMO-UT模型。该模型的编码部分通过编码IoTD的信息与权重向量得到所有子问题的特征，实现了利用一个模型解决所有子问题的目的，从而提高了模型利用率。在解码器部分采用了轨迹搜索，提高了模型在轨迹生成时的探索能力与帕累托集的质量，减轻了陷入局部最优的现象。

然而，本文模型依然存在一些限制，本文所研究的MOP仅考虑了最小化能耗与AoI，而实际的数据收集系统中存在诸多指标需要优化，比如UAV的数量、任务完成时间等。因此，在未来研究中，将考虑更多的优化指标，并根据多个指标的特性进行优化，找到最合适的优化方法。

[1] CUI Q， WANG Y， CHEN K-C， et al. Big data analytics and network calculus enabling intelligent management of autonomous vehicles in a smart city ［J］. IEEE Internet of Things Journal， 2019， 6（2）： 2021-2034.

[2] VERMA P，SOOD S K. Fog assisted-IoT enabled patient health monitoring in smart homes ［J］. IEEE Internet of Things Journal， 2018， 5（3）： 1789-1796.

[3] PATHAK N， DEB P K， MUKHERJEE A， et al. IoT-to-the-rescue： A survey of IoT solutions for COVID-19-like pandemics ［J］. IEEE Internet of Things Journal， 2021， 8（17）： 13145-13164.

[4] HU H， XIONG K， QU G， et al. AoI-minimal trajectory planning and data collection in UAV-assisted wireless powered IoT networks ［J］. IEEE Internet of Things Journal， 2021， 8（2）： 1211-1223.

[5] YATES R D， SUN Y， BROWN D R， et al. Age of information： An introduction and survey ［J］. IEEE Journal on Selected Areas in Communications， 2021， 39（5）： 1183-1210.

[6] CHEN Z， CHI K， ZHENG K， et al. Minimization of transmission completion time in UAV-enabled wireless powered communication networks ［J］. IEEE Internet of Things Journal， 2020， 7（2）： 1245-1259.

[7] BOZORGCHENANI A， MASHHADI F， TARCHI D， et al. Multi-objective computation sharing in energy and delay constrained mobile edge computing environments ［J］. IEEE Transactions on Mobile Computing， 2021， 20（10）： 2992-3005.

[8] LIAO Y， FRIDERIKOS V. Energy and age Pareto optimal trajectories in UAV-assisted wireless data collection ［J］. IEEE Transactions on Vehicular Technology， 2022， 71（8）： 9101-9106.

[9] LIN X， YANG Z， ZHANG Q. Pareto set learning for neural multi-objective combinatorial optimization ［EB/OL］. （2022-03-29）［2022-08-10］. https：//arxiv.org/pdf/2203.15386.pdf.

[10] HELSGAUN K. An effective implementation of the Lin–Kernighan traveling salesman heuristic ［J］. European Journal of Operational Research， 2000， 126（1）： 106-130.

[11] 肖晓伟，肖迪，林锦国，等. 多目标优化问题的研究概述［J］. 计算机应用研究， 2011， 28（3）： 805-808， 827.（XIAO X W， XIAO D， LIN J G， et al. Overview on multi-objective optimization problem research ［J］. Application Research of Computers， 2011， 28（3）： 805-808，827.）

[12] FLORIOS K， MAVROTAS G. Generation of the exact Pareto set in multi-objective traveling salesman and set covering problems ［J］. Applied Mathematics and Computation， 2014， 237： 1-19.

[13] SRINIVAS N， DEB K. Muiltiobjective optimization using nondominated sorting in genetic algorithms ［J］. Evolutionary Computation， 1994， 2（3）： 221-248.

[14] DEB K， PRATAP A， AGARWAL S， et al. A fast and elitist multiobjective genetic algorithm： NSGA‑Ⅱ ［J］. IEEE Transactions on Evolutionary Computation， 2002， 6（2）： 182-197.

[15] GHAMBARI S， GOLABI M， LEPAGNOT J， et al. An enhanced NSGA‑Ⅱ for multiobjective UAV path planning in urban environments［C］// Proceedings of the 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence. Piscataway： IEEE， 2020： 106-111.

[16] ZHANG Q， LI H. MOEA/D： A multiobjective evolutionary algorithm based on decomposition ［J］. IEEE Transactions on Evolutionary Computation， 2007， 11（6）： 712-731.

[17] 周爱民，张青富，张桂戌.一种基于混合高斯模型的多目标进化算法［J］. 软件学报， 2014， 25（5）： 913-928.（ZHOU A M， ZHANG Q F， ZHANG G X. Multi-objective evolutionary algorithm based on mixed Gaussian models［J］. Journal of Software， 2014， 25（5）： 913-928.）

[18] 侯薇，董红斌，印桂生.一种改进的基于分解的多目标进化算法［J］. 计算机科学， 2014， 41（2）： 114-118.（HOU W， DONG H B， YIN G S. Enhanced multi-objective evolutionary algorithm based on decomposition ［J］. Computer Science， 2014， 41（2）： 114-118.）

[19] LAURENT P， VINCENT F. OR-Tools ［EB/OL］. （2022-11-25）［2023-11-29］. https：//developers.google.com/optimization/.

[20] COOK W. Concorde ［EB/OL］. （2003-11-05）［2022-12-05］. https：//www.math.uwaterloo.ca/tsp/concorde.html.

[21] GU Z H， ROTHBERG E， BIXBY R. Gurobi ［EB/OL］. （2021-11-16）［2022-12-05］. https：//www.gurobi.com.

[22] SUTSKEVER I， VINYALS O， LE Q V. Sequence to sequence learning with neural networks ［C］// Proceedings of the 27th International Conference on Neural Information Processing Systems-Volume 2. New York： ACM， 2014： 3104-3112.

[23] VINYALS O， FORTUNATO M， JAITLY N. Pointer networks ［C］// Proceedings of the 28th International Conference on Neural Information Processing Systems-Volume 2. New York： ACM， 2015： 2692-2700.

[24] KOOL W， VAN HOOF H， WELLING M. Attention， learn to solve routing problems！［EB/OL］. （2018-03-22）［2022-08-29］. https：//arxiv.org/pdf/1803.08475.pdf

[25] LI K， ZHANG T， WANG R. Deep reinforcement learning for multiobjective optimization ［J］. IEEE Transactions on Cybernetics， 2021， 51（6）： 3103-3114.

[26] WU H， WANG J， ZHANG Z. MODRL/D-AM： multiobjective deep reinforcement learning algorithm using decomposition and attention model for multiobjective optimization ［C］// Proceedings of the 11th International Symposium on Artificial Intelligence Algorithms and Applications. Singapore： Springer， 2020： 575-589.

[27] ZHANG Y， WANG J， ZHANG Z， et al. MODRL/D-EL： multiobjective deep reinforcement learning with evolutionary learning for multiobjective optimization ［C］// Proceedings of the 2021 International Joint Conference on Neural Networks. Piscataway： IEEE， 2021： 1-8.

[28] 董健，钦文雯，李莹娟，等. 基于改进反向传播神经网络代理模型的快速多目标天线设计［J］. 电子与信息学报， 2018， 40（11）： 2712-2719.（DONG J， QIN W W， LI Y J， et al. Fast multi-objective antenna design based on improved back propagation neural network surrogate model ［J］. Journal of Electronics & Information Technology， 2018， 40（11）： 2712-2719.）

[29] 黄博南，王勇，李玉帅，等. 基于分布式神经动态优化的综合能源系统多目标优化调度［J］. 自动化学报， 2022， 48（7）： 1718-1736.（HUANG B N， WANG Y， LI Y S， et al. Multi-objective optimal scheduling of integrated energy systems based on distributed neurodynamic optimization ［J］. Acta Automatica Sinica， 2022， 48（7）： 1718-1736.）

[30] KWON Y D， CHOO J， KIM B， et al. POMO： policy optimization with multiple optima for reinforcement learning ［J］. Advances in Neural Information Processing Systems， 2020， 33： 21188-21198.

[31] DAI H， KHALIL E， ZHANG Y， et al. Learning combinatorial optimization algorithms over graphs ［C］// Proceedings of the 31st International Conference on Neural Information Processing Systems. Red Hook： Curran Associates Inc.， 2017： 6351-6361.

[32] YANG L， WANG S， CHEN X， et al. High-fidelity permeability and porosity prediction using deep learning with the self-attention mechanism ［J］. IEEE Transactions on Neural Networks and Learning Systems， 2023， 34（7）： 3429-3443.

[33] NAIR V， HINTON G E. Rectified linear units improve restricted Boltzmann machines［C］// Proceedings of the 27th International Conference on Machine Learning. New York： ACM， 2010： 807-814.

[34] VASWANI A， SHAZEER N， PARMAR N， et al. Attention is all you need ［J］. Advances in Neural Information Processing Systems， 2017， 30： 6000-6010.

[35] KATHAROPOULOS A， VYAS A， PAPPAS N， et al. Transformers are RNNs： fast autoregressive transformers with linear attention［C］// Proceedings of the 37th International Conference on Machine Learning. New York： ACM， 2020： 5156-5165.

[36] CLEVERT D-A， UNTERTHINER T， HOCHREITER S. Fast and accurate deep network learning by exponential linear units （ELUs）［EB/OL］. （2015-11-23）［2022-12-26］. https：//arxiv.org/pdf/1511.07289.pdf.

[37] FANELLO S R， NOCETI N， CILIBERTO C， et al. Ask the image： supervised pooling to preserve feature locality ［C］// Proceedings of the 27th IEEE Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE， 2014： 851-858.

[38] WILLIAMS R J. Simple statistical gradient-following algorithms for connectionist reinforcement learning［J］. Machine Learning， 1992， 8： 229-256.

[39] ISHIBUCHI H， SAKANE Y， TSUKAMOTO N， et al. Adaptation of scalarizing functions in MOEA/D： an adaptive scalarizing function-based multiobjective evolutionary algorithm ［C］// Proceedings of the 2009 International Conference on Evolutionary Multi-Criterion Optimization. Berlin： Springer， 2009： 438-452.

[40] NAZARI M， OROOJLOOY A， TAKÁČ M， et al. Reinforcement learning for solving the vehicle routing problem ［C］// Proceedings of the 32nd International Conference on Neural Information Processing Systems. Red Hook： Curran Associates Inc.， 2018： 9861-9871.

[41] RIQUELME N， VON LÜCKEN C， BARAN B. Performance metrics in multi-objective optimization ［C］// Proceedings of the 41st Latin American Computing Conference. Piscataway： IEEE， 2015： 1-11.

[42] ZITZLER E， THIELE L， LAUMANNS M， et al. Performance assessment of multiobjective optimizers： an analysis and review ［J］. IEEE Transactions on Evolutionary Computation， 2003， 7（2）： 117-132.

Multi-objective optimization model for unmanned aerial vehicles trajectory based on decomposition and trajectory search

LIU Junyan1， JIANG Feibo1*， PENG Yubo1， DONG Li2

（1，，410081，；2，，410205，）

The traditional Deep Learning （DL）-based multi-objective solvers have the problems of low model utilization and being easy to fall into the local optimum. Aiming at these problems， a Multi-objective Optimization model for Unmanned aerial vehicles Trajectory based on Decomposition and Trajectory search （DTMO-UT） was proposed. The proposed model consists of the encoding and decoding parts. First， a Device encoder （Dencoder） and a Weight encoder （Wencoder） were contained in the encoding part， which were used to extract the state information of the Internet of Things （IoT） devices and the features of the weight vectors. And the scalar optimization sub-problems that were decomposed from the Multi-objective Optimization Problem （MOP） were represented by the weight vectors. Hence， the MOP was able to be solved by solving all the sub-problems. The Wencoder was able to encode all sub-problems， which improved the utilization of the model. Then， the decoding part containing the Trajectory decoder （Tdecoder） was used to decode the encoding features to generate the Pareto optimal solutions. Finally， to alleviate the phenomenon of greedy strategy falling into the local optimum， the trajectory search technology was added in trajectory decoder， that was generating multiple candidate trajectories and selecting the one with the best scalar value as the Pareto optimal solution. In this way， the exploration ability of the trajectory decoder was enhanced during trajectory planning， and a better-quality Pareto set was found. The results of simulation experiments show that compared with the mainstream DL MOP solvers， under the condition of 98.93% model parameter quantities decreasing， the proposed model reduces the distribution of MOP solutions by 0.076%， improves the ductility of the solutions by 0.014% and increases the overall performance by 1.23%， showing strong ability of practical trajectory planning of DTMO-UT model.

trajectory planning; Deep Learning (DL); multi-objective optimization; decomposition; Pareto set

This work is partially supported by National Natural Science Foundation of China （41904127）.

LIU Junyan， born in 1998， M. S. candidate. His research interests include deep learning， combinatorial optimization.

JIANG Feibo， born in 1982， Ph. D.， association professor. His research interests include deep learning， reinforcement learning， federated learning.

PENG Yubo， born in 1996， M. S. candidate. His research interests include edge computing， federated learning.

DONG Li， born in 1982， Ph. D.， association professor. Her research interests include deep learning， reinforcement learning.

TP183

A

1001-9081（2023）12-3806-10

10.11772/j.issn.1001-9081.2022121882

2022⁃12⁃22；

2023⁃03⁃15；

2023⁃03⁃17。

国家自然科学基金资助项目（41904127）。

柳隽琰（1998—），男，湖南岳阳人，硕士研究生，主要研究方向：深度学习、组合优化；江沸菠（1982—），男，湖南长沙人，副教授，博士，主要研究方向：深度学习、强化学习、联邦学习；彭于波（1996—），男，重庆人，硕士研究生，主要研究方向：边缘计算、联邦学习；董莉（1982—），女，湖南长沙人，副教授，博士，主要研究方向：深度学习、强化学习。