基于长记忆性特征的欧式回望期权模糊定价研究

□ 韦才敏 于 涛 王文华

（1.汕头大学 数学系，广东 汕头 515063；2.大连理工大学 商学院，辽宁 盘锦 124221）

一、引 言

期权作为市场上一种常见的金融衍生品，具备套期保值和规避风险等功能，因此对其进行精确且合理的定价具有重要的理论与实践意义。1973 年,Black 和Scholes[1]在假定股票价格满足对数正态分布的基础上，提出了著名的欧式期权定价模型, 奠定了期权定价研究的理论基础。但是随着经济和金融业的快速发展，投资者的投资需求更加细化，传统的欧式期权显然已不能满足实际金融市场的需求, 这就迫切要求对期权的种类进行改造与创新。回望期权是一种典型的对路径依赖的奇异期权，其敲定价格取决于期权有效期内的原生资产价格，期权持有者选取最低（最高）的原生资产价格作为敲定价格, 并以此购入（售出）一定量的原生资产。由于回望期权可以使期权的持有者在行权期间获得最大的可能收益，这也使得该类期权的价格会高于标准的欧式期权。近几十年来，众多学者对回望期权进行了大量研究[2-5]。

以往关于期权定价的研究大多是在Black-Scholes 模型上建立的，假定股票的对数收益率服从正态分布，使用几何布朗运动描述股票价格的变化过程。然而，一系列实证研究发现：在实际的金融市场中，当前股票价格会对未来价格产生持续的影响，即股票价格会呈现出长程相关性和自相似性，具有“尖峰厚尾”的特征[6]。为了便于刻画该特征，Mandelbrot[7]和Peters[8]将分形的概念引入到经济系统中，提出了“分形市场假说”，使用Hurst 指数H 刻画对数收益率的自相关性，对市场收益率的时间序列进行了研究。但是，分数布朗运动不具备鞅的良好性质，且会出现市场套利。因此，在描述股价变化时，单一地运用几何布朗运动或分数布朗运动总会存在以上问题。于是，Shiryaev 等[9]提出了混合分数布朗运动的概念，即利用两者的线性组合形式来刻画股价的变化过程，从而避免了这两类问题的出现。并且，Cheridito[10]证明了在Hurst 指数H∈ (0.75,1)的条件下，市场是无套利的，可以利用几何布朗运动的鞅性对期权价格进行研究。Rao[11]用混合分数布朗运动刻画股票价格的变化，给出了考虑长记忆性特征的亚式期权定价公式。Ahmadian[12]基于标准无套利的论点，研究了混合分数布朗运动下亚式彩虹期权的定价问题。尤左伟等[13]则建立了在混合分数布朗运动环境下可转债的定价模型，利用风险中性定价原理得出了可转债定价公式。赵明清等[14]研究了银行存款再保险问题，推导出混合分数布朗运动下溢额再保险的定价公式，并通过实证分析验证了模型的实用性。孙晓霞[15]等证明了在非Lipschitz 条件下, 由混合分数布朗运动驱动的随机微分方程解的矩估计和连续性。

面对投资者的多种需求，仅考虑随机性的定价模型已经不能满足实际金融市场的发展。同时，金融市场经常会被一些模糊因素所影响，因此迫切需要在随机和模糊环境下研究期权定价的相关问题。与随机性不同的是，模糊性是用来描述当投资者不知道股票的确切收益时，对是否进行投资以及投资份额产生的不确定性。1965年，Zadeh[16]提出的模糊集理论成为刻画金融市场模糊性的重要理论基础。Wu[17]给出了模糊集理论在B-S 模型中的应用，建立了模糊环境下欧式期权的定价模型，得到了任意期权价格的置信度，使得投资者可以按照任何具有可接受的信任程度选择期权的价格。Zhang 等[18]认为定价公式中输入的数据会随市场的波动而具有不确定性，因此在模糊环境下讨论了期权的定价问题，推导出了几何亚式期权的模糊价格公式，并使用插值搜索算法确定置信度，通过数值算例验证了模型的合理性与实用性。秦学志等[19]研究了三角模糊数下欧式期权的定价问题，构建了基于三角模糊数的欧式期权模糊定价模型。为了更好地刻画投资者对期权价格估计值的肯定、否定及犹豫程度，张茂军等[20]首次将三角直觉模糊数引入欧式期权中，建立了基于三角直觉模糊数的二叉树定价模型。明雷等[21]给出了三角直觉模糊数下Black-Scholes模型的期权解析式，推广了Yoshida 的相关结论，并对模型的稳定性和灵敏性进行了分析。

综上所述，本文结合已有文献结论及其存在的不足之处，在B-S 模型的基础上，考虑了金融市场存在的长记忆性特征和投资行为的犹豫性，建立了一种新的欧式回望期权定价模型。本文的学术贡献主要体现在：首先，选取标的股票初始价格作为模糊变量，构建了混合分数布朗运动下，欧式回望看涨期权的模糊定价模型；其次，论证了期权的模糊价格关于模糊变量的单调性，并给出了不同情形下期权的价格截集，期权持有者可根据自身需求及对风险的承受能力，选择合理的犹豫程度，补充了现有关于欧式回望期权定价文献的不足；然后，通过理论推导与数值实验，验证了长记忆性指标Hurst 指数H 对期权价格的影响，并揭示出该影响与行权时间T 相关；最后，对模型中的各个参量进行了数值分析，给出了期权价格截集变化的经济学解释，对模型的可行性和合理性进行了验证。

其余部分组织如下：第一节中，本文介绍了关于混合分数布朗运动和三角直觉模糊数的基础知识，并将长记忆性和模糊性融入到传统的欧式回望期权定价模型中，给出了期权的模糊定价公式，推导出了期权的价格截集及Hurst 指数H 对定价模型影响的相关定理；第二节中，本文进行了数值分析，对模型的长记忆性和其他参量对于期权价格截集的影响进行了检验，并对实验结果进行了解释，表明与理论推导一致；最后，第三节是本文的结论与展望。

二、混合分数布朗运动下欧式回望期权的模糊定价模型

定义1(混合分数布朗运动)[22]在一个完备的概率空间( Ω, F,P)中，定义混合分数布朗运动(α,β)与几何布朗运动tB、分数布朗运动的线性关系如下，

（ii）对任意H＞0,(α,β)的增量是任意的和混合自相似的，；

（iii）当0.5＜H＜ 1时，(α,β)的增量是长程且正相关的。

定义2 ( 三角模糊数)[20]设实数集R上的模糊集= (a1,a,a2)，其隶属度函数定义如下:

满足如上定义的模糊数，即为三角模糊数。

定义3 （三角直觉模糊数）[20]=＜ (a1,a,a2);,＞为定义在实数集R 上的三角直觉模糊数( 图1)，其隶属和非隶属函数定义分别为：

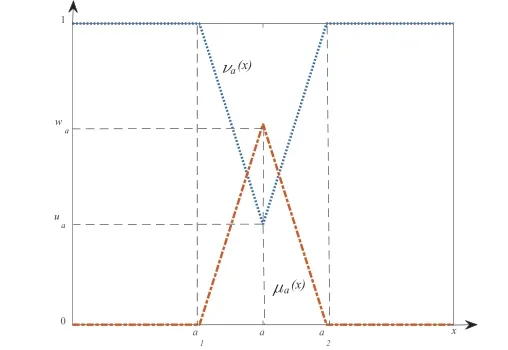
图1 三角直觉模糊数

首先，给定具有σ- 流的完备概率空间( Ω,F,P)及对应的域流{Ft,t∈ [0,T]}，假设模糊变量为标的股票的初始价格，金融市场上的现金市场Mt和股票可以进行自由、连续的交易，允许买空卖空且市场无套利，期权到期日为时间T。

其中：µ、σ均为常数，表示股票收益率和波动率。

最后，现金市场Mt满足：dM t=rM tdt,M0= 1 , 0≤t≤T,r表示无风险利率，不考虑支付交易费、税收及红利。

（i）利用Δ-对冲原理，形成投资组合[23]：∏ =V-ΔSt，适当选取份额Δ，使得Π 在(t,t+dt)是无风险的，即有dΠ=rΠdt,由公式得

从而（8）可简化为：

（iii）欧式回望看涨期权在T 时刻的模糊收益为：

边界条件为：

定理1 欧式回望看涨期权的模糊定价公式：

其中

证明：由以上的讨论知回望看涨期权满足如下条件

将(16)代入(15)后得到

令u(x,t) =eαx+β(T-t)·W(x,t),代入式(17)

令大括号中的式子恒为0，有

得

采用镜像法求解，令

又因为 Φ(x) 满足方程组

参照文献[23]知方程(19)的解存在且唯一，由Poisson公式，该方程的解可表为，代回原变量(S,J,t) 及函数V 即得结果，证毕。

在得到欧式回望看涨期权的模糊定价公式后，为了进一步得到期权的价格截集，需引入相关概念：

对应α-截集与β- 截集的定义，股票模糊初始价格的两类价格截集可表示如下:

α- 截 集：，β- 截 集 为：。

参照Yoshida[22] 的相关研究，令at=cSt，c表示模糊指标，则S1:=S t-at、S2:=S t+at。

记Δ=α(1 -uS～) - (1 -β)wS～，当Δ ＞ 0时，；当Δ ≤ 0时，。

定理3 （期权模糊价格对股票模糊初始价格的单调性判断）欧式回望看涨期权的模糊价格是关于标的股票模糊初始价格的单调递增函数。

将以上关系代入（20）有

由上式可得当θ取值较大时，可使≥0;以下继续判定的正负性，

证毕。

定理4 两类欧式回望看涨期权tV的价格截集：

（1） 当Δ ＞0 时，

其中。

（2） 当Δ ≤0 时，

定理3 证明了股票的模糊初始价格越高，期权的模糊价格也会越高，故在式(14)中将1I、I2依次替换并代入，得到并代入期权的模糊定价公式中，即为期权的价格截集，证明从略。

注1：当不考虑投资者的犹豫程度，即c= 0时，欧式回望看涨期权Vt的价格区间退化为一个数，I0=St。

这正是确定环境下，只考虑长记忆性特征的回望看涨期权的定价公式。

则平方后

注意到（29）各式中均含有T2HlnT-t2Hlnt,提取公因式即得结论，证毕。

注2：定理5 表明了T 的取值将会改变长记忆性指标H 对期权价格的影响。

三、数值实验

在第二节中主要进行了理论推导，包括建立了混合分数布朗运动下欧式回望期权的模糊定价模型，给出了期权的价格截集及对模型的长记忆性特征进行了研究等。本节在此基础上，将运用数值实验的方法对上述结论进行检验，首先研究Hurst 指数H 对期权模糊价格的影响；然后对期权的价格截集运用控制变量法，分析了模型的稳健性，给出了对应的经济学解释。其中：期权价格截集的上限价格用I2表示，下限价格用I1表示。

(一)基准模型的参数数据

当Δ ＞ 0时的基准数据：股票初始价格S= 25，期权期限t= 1，T= 2，Hurst 指数H= 0.76，无风险利率r=0.10，股票波动率σ= 0.10，α-截集α=0.75，最低价格J= 23，最大隶属度= 0.9，β- 截集β=0.2，最小非隶属度= 0.05，模糊指标c=0.05；当Δ ≤ 0时结论类似。图中虚线表示期权上限价格I2，实线表示期权下限价格I1。

(二)Hurst 指数H 对定价模型的影响

由定理5 知，在期权的模糊价格对H 求导后可提取公因式T2HlnT-t2Hlnt，这表明长记忆性对期权价格的影响会受到行权时间T 的作用。如图2 和图3 所示，本文在此理论基础上选取了两种不同的行权时间，可得出如下结论：当T＜1 时，期权的模糊价格随H 的增大而减小，当T＞1 时，期权的模糊价格随H 的增大而增大。

图2 T =0.5时，期权价格对H 的偏导

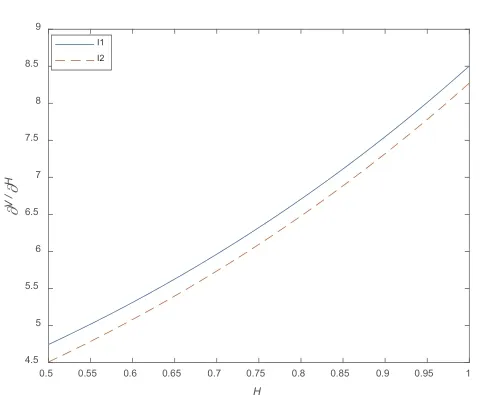
图3 T =1.45时，期权价格对H 的偏导

(三)灵敏性和稳健性分析

本节讨论了欧式回望期权的定价模型中，各个因素对期权价格截集的影响，并给出相应的经济学解释。

图4 和图5 分别展现了无风险利率r和波动率σ对期权价格截集的影响。在证明期权的模糊价格关于初始价格S为单调递增函数时，曾令θ的取值适当大，而这就要求无风险利率r的取值不宜过小、波动率σ的取值不宜过大。从图中可知，期权的上下限价格随无风险利率r、波动率σ的增大而增大。

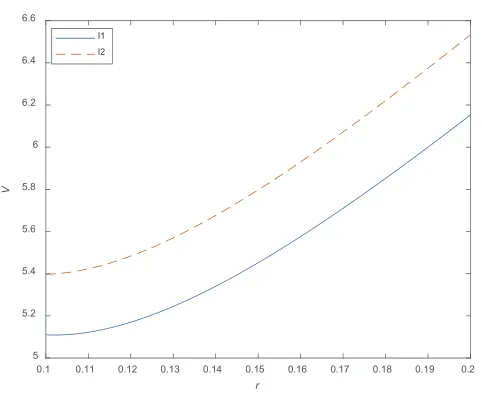
图4 无风险利率r 对期权价格的影响

图5 波动率σ 对期权价格的影响

图6 验证了定理3 的结论，表明了欧式回望看涨期权的价格会随初始股价S的增大而增大。图7 反映了在回望看涨期权中，最低价格J对期权价格的影响。 由欧式回望看涨期权的收益函数可知，股票的最低价格越大，期权持有者的收益也就越小，期权价格也应适当减小。而这与图7中期权价格是关于股票最低价格的单调递减函数相一致。

图6 初始价格S 对期权价格的影响

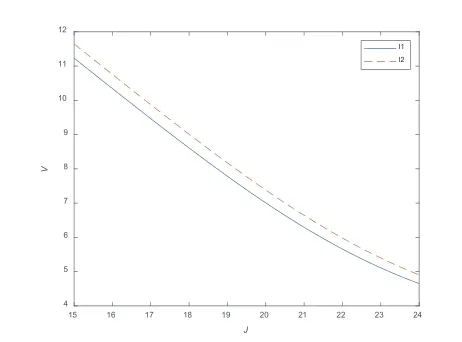
图7 最低价格J 对期权价格的影响

从图8 可以看出，可行度 对欧式回望看涨期权上下限价格的影响是相反的；意味着 越大，欧式回望看涨期权的定价区间越小，即越小。这满足了不同投资者的需求，对于相对保守的投资者，他们可以使用较高的可行度，但最大收益会较低；而对于那些较为激进投资者来说，他们可能会有更多的收益，但同时也伴随着更大的风险。图9反映了最大隶属度对期权价格的影响，隶属度用来描述不确定量的隶属程度，随着最大隶属度的增加，投资者的犹豫程度会减小，即变大，但不应过大，否则便失去了期权价格区间的估计作用；且当时，期权的上下限价格相等，故此时的取值也不应小于0.75。

图8 可行度α 对期权价格的影响

图9 最大隶属度 sw～ 对期权价格的影响

图10 反映了模糊指标c 对期权价格的影响，表明该参量对期权价格的影响为线性的。由于c=，c 越大，投资者承受风险的能力越高，可选择进行投资的区间也应越大，在图中表现为期权价格截集的区间长度I2-I1越大，因此投资者可根据自身需求进行合理的投资。

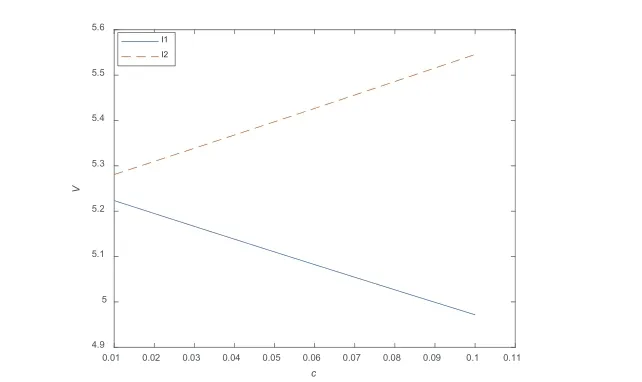
图10 模糊指标c 对期权价格的影响

四、结论

欧式回望期权是一种典型的强路径依赖期权，对其进行准确合理的定价是具有重要理论和实践意义的。与已有文献的不同之处在于，本文从随机性和模糊性两方面刻画了金融市场存在的不确定性，并且运用混合分数布朗运动描述了股票价格的长记忆性特征，建立了基于三角直觉模糊数的欧式回望期权定价模型，该模型更具有普遍性和现实意义。取得的主要结论如下：一，假定股票的价格变化满足混合分数布朗运动，并将标的股票的初始价格设为模糊变量，结合已有文献推导出了欧式回望期权的模糊定价公式。二，论证了期权的模糊价格是关于标的股票模糊初始价格的单调递增函数，并在此基础上给出具体的期权价格截集公式。投资者可以根据自身需求，对可行度α及模糊指标c 进行适当的调节，确定期权价格区间。比如投资者可选择较大的犹豫程度，相应的投资区间也会较大，风险和收益都会更高。三，研究了模型的长记忆性特征，从理论和数值实验上证明了Hurst 指数H 对期权价格的影响将会受到行权时间T 的作用。四，对影响期权价格截集的其他参数，如：无风险利率、波动率和模糊指标等进行了数值实验，将理论推导和实验结果相结合，从经济学的角度表述了不同参数对欧式回望看涨期权价格的影响。最后，在该领域还有很多问题可以进一步研究，例如金融市场中存在着一些突发状况，会使股票价格发生大的上下跳跃，因此可以考虑在分数跳跃- 扩散过程上建立欧式回望期权和障碍期权的定价模型；同时模糊性的研究也可以拓展到其他金融衍生品等。