重力位三阶梯度张量异常的波数域转换计算及其DEXP定量解释方法
邱 峰
(江西省水利科学院 建材与岩土研究所,江西 南昌 330029)
0 引言
重力位三阶梯度张量是重力位在坐标轴3个方向的三阶导数,表示重力梯度张量各个元素在3个方向上的空间变化率,相比传统的重力异常数据以及重力梯度异常数据,其对于微弱的密度差异引起的变化更为敏感。在重力勘探及大地测量领域,测量地球的重力位场的三阶导数及其时变场最早是由Balakin等[1]于1997年在Dulkyn项目中提出。之后基于此思想与概念,DiFrancesco等[2]在2009年提出重力三阶梯度张量的航空测量概念,Brieden等[3]又在2010年提出利用卫星测量地球时变重力场的计划。同时,Fantino等[4]和Casotto等[5]以及Fukushima[6]从2009~2013年相继发表了阐述重力位一阶至三阶梯度的球谐表达式及其计算问题的相关系列论文。而Rosi等[7]于2015年在实验室内利用冷原子干涉技术测量重力位三阶垂直梯度的成功实现,使得重力位三阶梯度张量研究取得突破性的进展。此外,由于重力位三阶垂向梯度对局部质量源具有高度敏感性,也被用于实验室测量万有引力常数[8];并且,由于地球重力位三阶垂直梯度具有不为零的特点,使得重力垂直梯度随高度变化存在非线性特征[9]。目前,重力位三阶梯度张量测量技术已经初见雏形,随着其将来的进一步发展,势必在重力勘探以及大地测量等领域引起新一轮的技术革命。
DEXP(depth from extreme point)变换成像法是近几年刚被提出并且发展较快的一种方法,由Fedi[10]提出,由于在计算过程中深度加权函数加入了异常体对应的构造指数,使得相比于其他成像结果更为准确。该方法的适用性比较广,不仅可以用于重力异常不同阶次导数来估计异常体的物性参数(如场源深度、剩余密度及构造指数等),也可以应用于自然电位数据处理,并有较好的结果[11]。由于重力位三阶梯度张量具有7个独立元素,因此其空间分布形态丰富多样,能够获取比传统重力异常以及重力梯度张量更多的场源信息[12],并且采用重力位三阶梯度张量异常进行DEXP定量解释具有更强的抗噪能力、受背景场影响也更小[13]。
由于重力位三阶梯度张量勘探方法还没有提出完善的测量体系,尚处于概念提出与理论基础研究阶段,因此在实际数据资料处理中,只能通过基于重力异常或重力梯度张量数据进行数据转换得到所需要的重力位三阶梯度张量数据。波数域数据转换计算方法是其中较为常用且有效的方法之一[14-15]。重力位三阶梯度张量波数域转换计算方法还未见国内外学者进行报道或发表,因此本文首先推导重力位三阶梯度张量的波数域转换计算公式,然后利用理论模型进行试验对比验证,最后将该方法应用到Vinton盐丘区DEXP数据处理中,取得较好的结果。
1 方法原理
1.1 重力位三阶梯度张量异常的波数域转换计算方法
1.1.1 基于重力异常的波数域转换计算方法
对于自由空间的重力矢量g(x,y,z) = (gx,gy,gz),其3个分量是连续可微的。Mickus等[14]根据拉普拉斯方程得到了重力矢量各分量的傅里叶变换式:
(1)
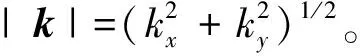
重力位三阶梯度张量是重力三分量在x、y以及z方向上的二阶导数,即Wαβγ=∂2gα/(∂β∂γ),∀{α,β,γ}∈{x,y,z},其仅有7个独立元素。因此根据式(1),由重力异常数据得到重力位三阶梯度张量数据的表达式为:
(2)
1.1.2 基于重力梯度张量的波数域转换计算方法
根据式(1)同样可得重力梯度张量的傅里叶转换表达式,Mickus等[14]已经得到基于重力异常数据波数域转换重力梯度张量的表达式:
Tij= FFT-1{[K(k)]Gz(k)},
(3)
其中:
。
(4)
由于重力三阶梯度张量是重力梯度张量在坐标轴3个方向上的导数,所以结合式(4)即可得基于重力梯度张量数据波数域转换重力三阶梯度张量的表达式:
(5)
其中:Гij为重力梯度张量各分量的二维离散快速傅里叶变换。
1.2 重力位三阶梯度张量异常的比值DEXP定量解释方法
根据Fedi[10]提出的DEXP变换方法理论可知,重力位异常在坐标轴3个方向上的p阶导数的DEXP变换函数可表示为:
Ωp=zNp/2fp,
(6)
其中:zNp/2为p阶DEXP变换的深度加权函数;fp为重力位异常p阶导数。
由于重力位三阶梯度张量异常为重力位在坐标轴x、y、z方向得到三阶导数,所以式(6)中Np可以写成N3=N+3,因此重力位三阶梯度张量各分量的DEXP变换函数为:
(7)
2 模型试验
首先令均匀直立棱柱体模型(如图1所示)的长(a)、宽(b)及高(c)分别为150 m、100 m以及60 m,剩余密度为0.5 g/cm3,中心埋深为100 m,计算点距为2 m,观测面为地面即z=0 m。直立棱柱体重力位一阶至三阶重力梯度正演公式众多文献已给出[16],因此可得模型重力位一阶至三阶重力梯度张量异常,如图2所示。
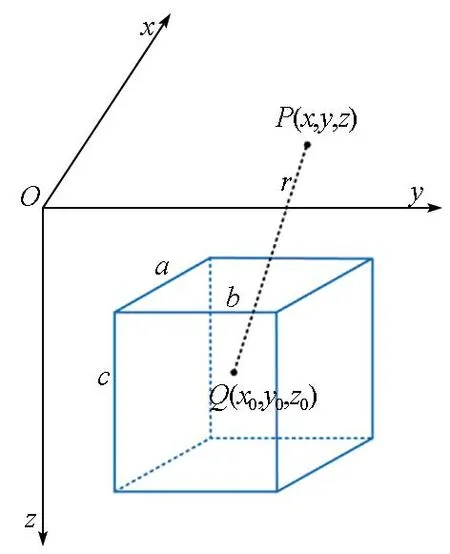
图1 直立长方体模型几何示意Fig.1 Geometric schematic diagram of upright cuboid model
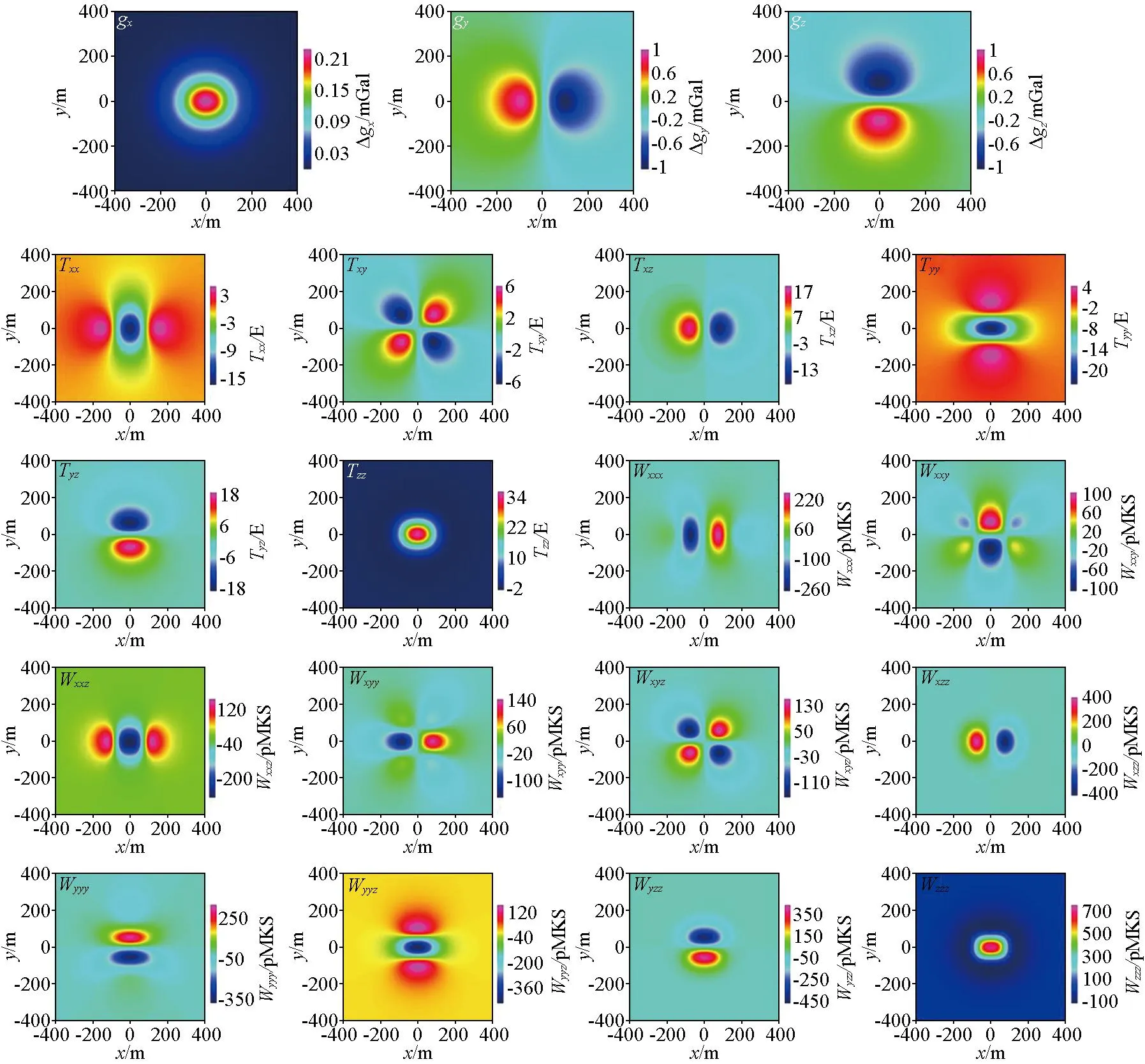
图2 模型重力位一阶至三阶张量异常空间分布Fig.2 The gravity tensor anomalies from first-order to third-order of upright cuboid model
2.1 基于重力异常的重力位三阶梯度张量异常转换计算
根据式(2)可知,为得到重力位三阶梯度张量各分量结果,首先须将重力异常模拟数据进行二维离散快速傅里叶变换(FFT),再乘以各分量对应的转化系数计算各自的频谱,最后再对所得频谱分别进行二维离散快速傅里叶反变换(IFFT),即可得到模拟数据的转换结果。本文提出的重力位三阶梯度张量计算算法使用到了二维离散快速傅里叶变换方法,因此FFT转换计算结果会存在一定的误差。为了直观地说明重力位三阶梯度张量FFT转换计算结果与模型正演计算结果的差异,本文计算并可视化了模型对应的每个分量之间的误差,如图3所示。由图可知,Wxxy、Wxyy、Wxyz分量的误差较小,误差绝对值最大不超过1.6 pMKS;但剩余的7个分量(Wxxx、Wxxz、Wxzz、Wxyy、Wyyz、Wyzz、Wzzz),由于FFT计算过程中受边界效应影响较大,使得分布在计算边界的数据结果误差也比较大,其误差较大的数据值分布在x、y剖面上-400~ -380 m和380~ 400 m范围之间,如果去除这些受边界效应影响较大的数据,则重力位三阶梯度张量FFT转换与正演计算之间的差异较小。
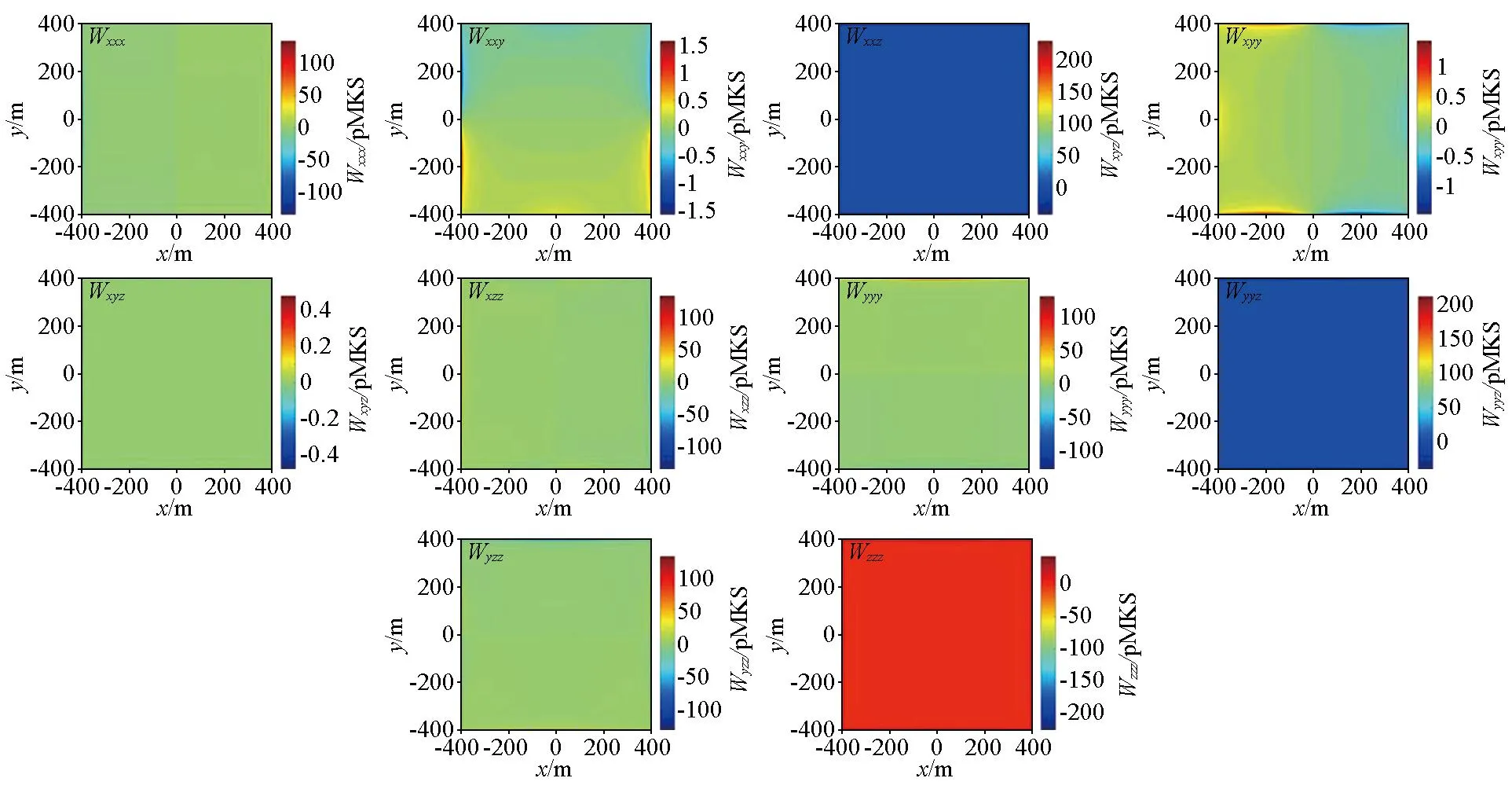
图3 基于重力异常的重力位三阶梯度张量FFT转换与正演计算各分量之间的差异Fig.3 The deviations between the FFT-derived and model-calculated third-order gradient tensor of gravitational potential from gravity value
此外,通过均方根误差(RMS)来量化本文所使用方法存在的误差,其计算公式如下:
∀{α,β,γ}∈{x,y,z} ,
(8)
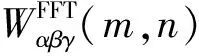
表1为正演模型重力位三阶梯度张量的均方根误差,其中去掉部分边界畸变值计算的是-390~390 m范围之间7个分量(Wxxx、Wxxz、Wxzz、Wxyy、Wyyz、Wyzz、Wzzz)的均方根误差。由表1可知,均方根误差比较大的是受边界影响较大的7个分量(Wxxx、Wxxz、Wxzz、Wxyy、Wyyz、Wyzz、Wzzz),其均方根误差均超过7 pMKS,RMS最大的为Wzzz分量;剩余的3个分量计算的均方根误差较小,均不超过0.2 pMKS,其中RMS最小的为Wxyz分量。对于去掉部分边界畸变值的计算结果,每个分量的均方根误差不超过2.55 pMKS,其中RMS最大的为Wxxx分量,RMS最小的为Wxyz分量。

表1 基于重力异常的重力三阶梯度张量异常转换计算结果与理论值间的均方根误差Table 1 RMS error between model and FFT third-order gradient tensor of gravitational potential
2.2 基于重力梯度张量异常的重力位三阶梯度张量异常转换计算
同理,根据式(5)可得出基于重力梯度张量波数域转换计算的重力位三阶梯度张量异常。为直观说明重力位三阶梯度张量FFT转换计算结果与模型正演计算结果的差异,同样计算并可视化了模型对应的每个分量之间的误差,如图4所示。由图可知,每个分量转换计算结果与模型正演计算结果的误差非常小,误差绝对值最大不超过2.2 pMKS,其中FFT转换计算误差最大的为Wzzz分量,误差最小的为Wxyz分量。
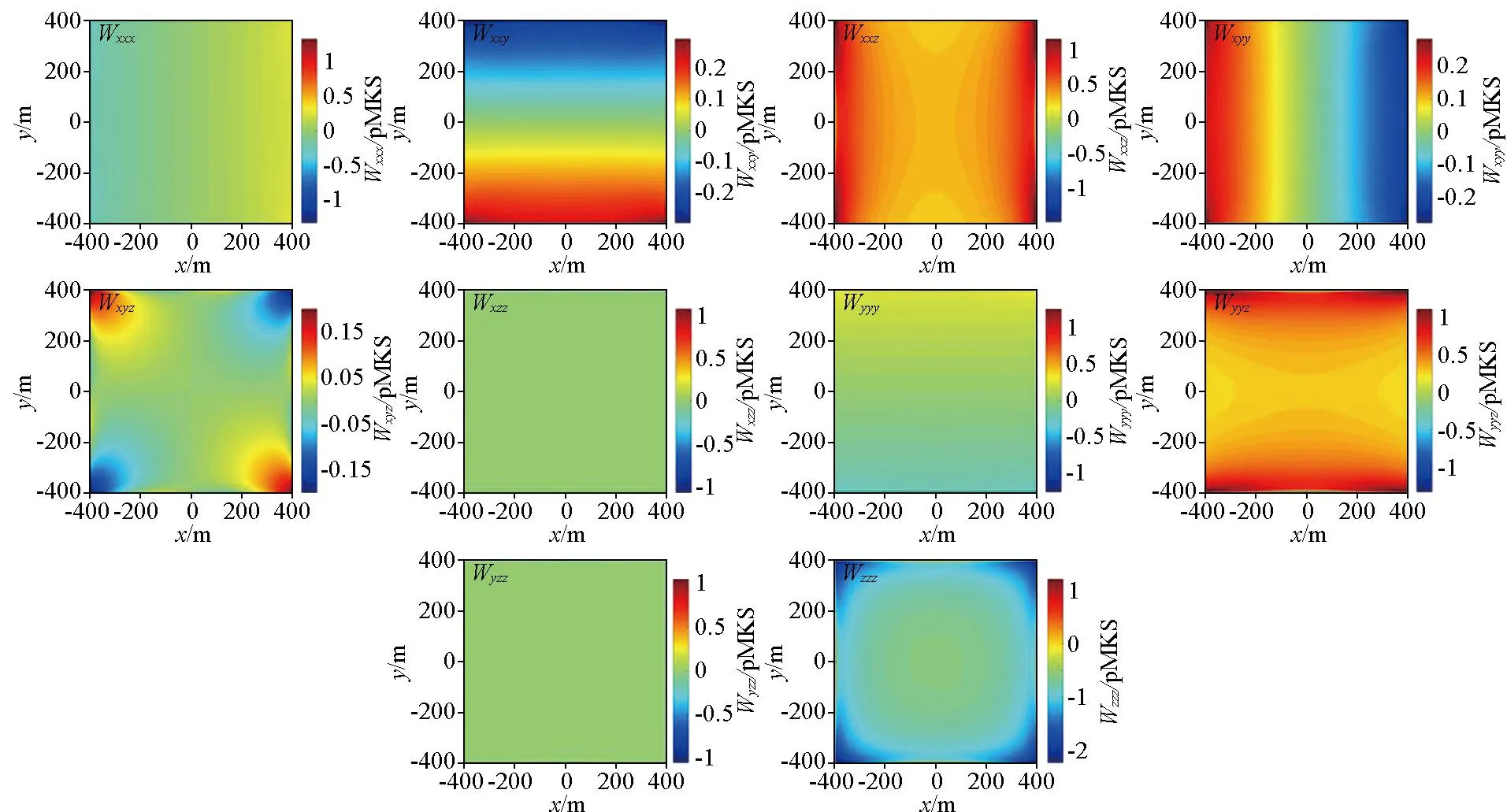
图4 基于重力梯度张量数据的重力位三阶梯度张量FFT转换与正演计算各分量之间的差异Fig.4 The deviations between the FFT-derived and model-calculated third-order gradient tensor of gravitational potential from gravity gradient tensor
通过式(8),可以计算出基于重力梯度张量数据的重力位三阶梯度张量FFT转换计算结果与理论值之间的均方根误差,如表2所示。由表可知,每个分量所计算的均方根误差都比较小,RMS最大不超过1 pMKS,对应为Wzzz分量,RMS最小为0.04 pMKS,对应为Wxyz分量。并且与重力异常数据的FFT转换计算结果相比,基于重力梯度张量的换算结果受边界效应的影响非常小,使得每个分量与理论值之间的误差也非常小,对应的均方根误差也很小,更接近理论值。

表2 基于重力梯度张量的重力三阶梯度张量异常转换计算结果与理论值间的均方根误差Table 2 RMS error between model and FFT third-order gradient tensor of gravitational potential
3 实际应用
3.1 数据及其预处理
本文所采用的文顿盐丘重力梯度张量(FTG)实测数据由Bell Geospace公司在2008年利用Air-FTG全张量重力梯度仪测量得到。其中,该测区范围为北纬30.07°~30.23°、西经93.53°~93.66°,总测线长度为1 087.5 km,测区面积为192.6 km2。在实际航空测量中,其飞行测线方向为SN向,其中,中间两侧53条测线间距为250 m,中间部分测线间距为125 m,航测飞行高度设定为80 m。由于数据量较大,为方便数据资料处理分析,本文只选取了面积较小的文顿盐丘测区。在实际异常数据资料的处理中,噪声以及区域背景场的存在往往会对数据处理结果产生较大的误差,尤其是背景场。因此,为提高后续数据处理结果的精度,先对实测重力异常以及重力梯度张量数据进行去噪处理,然后对去噪后的数据进行滤波,移除背景场。图5a~f为处理后的重力梯度张量异常数据。
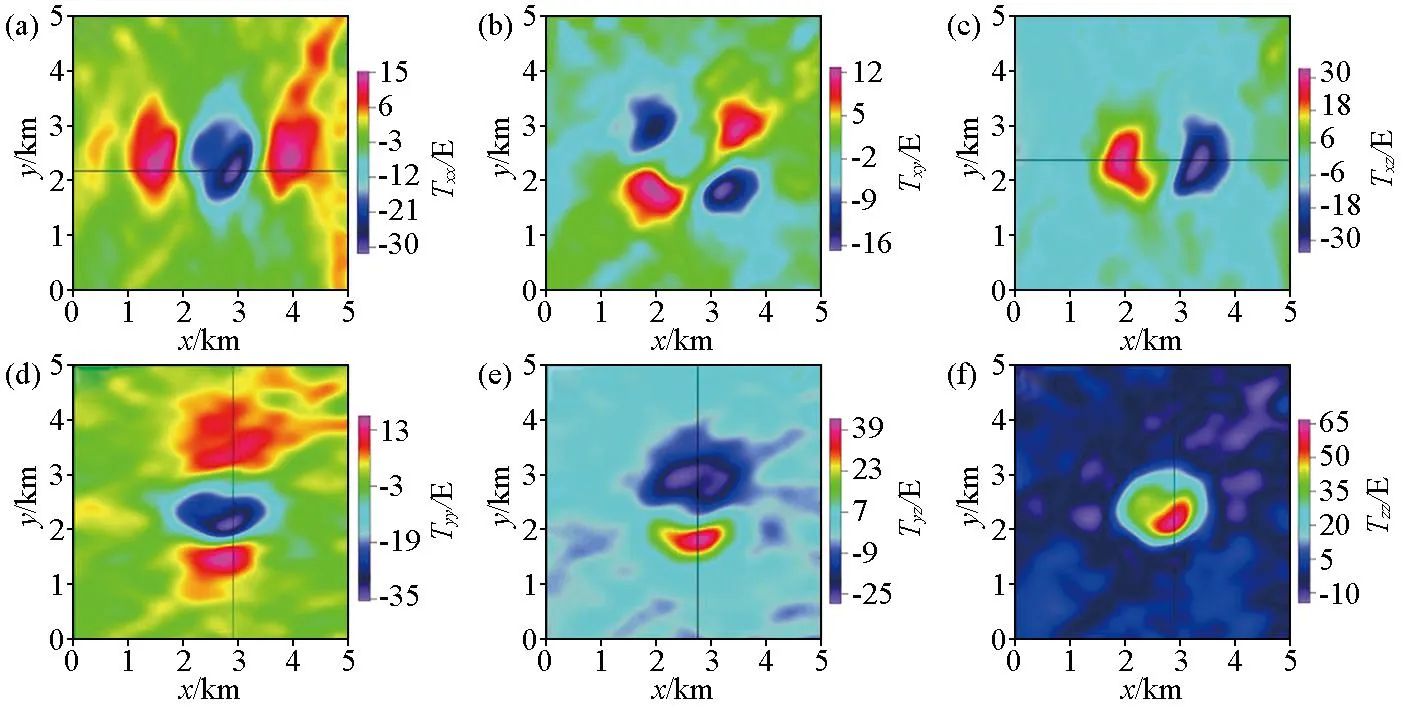
a—Txx异常;b—Txy异常;c—Txz异常;d—Tyy异常;e—Tyz异常;f—Tzz异常
3.2 重力位三阶梯度张量异常的转换计算结果
根据基于模型重力异常与重力梯度张量数据转换的重力位三阶梯度张量对比结果可知,由重力梯度张量转换的重力三阶梯度张量受边界效应的影响较低,计算结果精度更高。因此在本章实际数据资料处理中,结合前文数据波数域转换理论,采用如图5所示的经过处理后的Vinton盐丘区重力梯度张量数据进行波数域转换,即可得到该研究区较高精度的重力位三阶梯度张量异常数据,结果如图6所示。图中黑色实线为后续数据DEXP变换处理所选取的剖面位置。
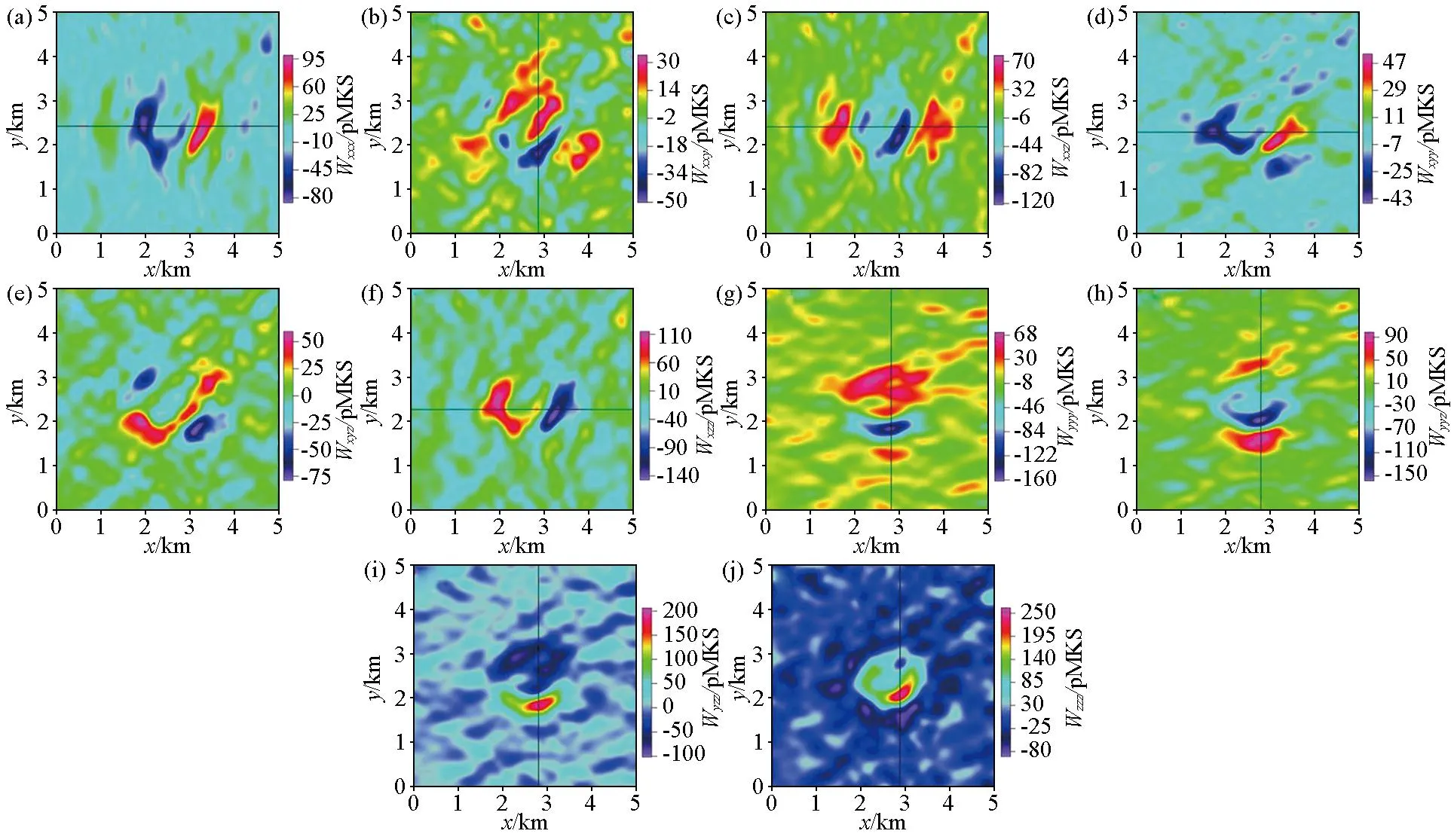
a—Wxxx;b—Wxxy;c—Wxxz;d—Wxyy;e—Wxyz;f—Wxzz;g—Wyyy;h—Wyyz;i—Wyzz;j—Wzzz
3.3 重力位三阶梯度张量异常的比值DEXP定量解释结果
根据DEXP理论,在对Vinton盐丘区实测数据进行DEXP变换处理时,需要预先知道该地区地下异常体的构造指数。根据Li[17]的研究可知,该盐丘体重力异常的构造指数为1.01,从而可以确定该盐丘体的重力位三阶梯度张量数据的构造指数为3.01。结合式(7),将波数域转换所得的重力位三阶梯度张量异常数据进行DEXP变换,即可得各分量所选剖面上的深度成像结果,如图7所示。
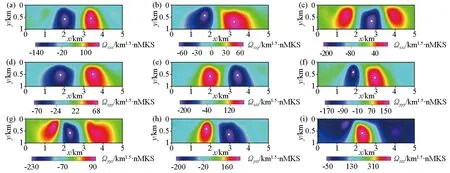
a—Ωxxx;b—Ωxxy;c—Ωxxz;d—Ωxyy;e—Ωxzz;f—Ωyyy;g—Ωyyz;h—Ωyzz;i—Ωzzz
由图7可知,能反映盐丘区深度信息的有Ωxxz结果(图7c)、Ωyyz结果(图7g)及Ωzzz结果(图7i),其各自的深度成像结果分别为580 m、660 m及600 m,减去航测飞行高度80 m,其反映的盐丘区平均埋藏深度约为533 m;Ωxxx结果(图7a)反映的是盐丘体EW向长度,其结果为1 350 m,Ωyyy结果(图7f)可以反映盐丘体SN向长度,其对应结果为1 125 m。Oliveria等[18]给出的盐丘区底面深度结果是460 m,Geng等[19]给出的底面深度结果是650 m,Ennen[20]给出Vinton盐丘区EW向长度为1 520 m,SN向长度为1 280 m。结合已知资料,认为本文所得结果是合理的。
4 结论
本文经过推导得到基于重力异常及重力梯度张量模拟数据的重力位三阶梯度张量波数域转换公式,并基于直立棱柱体模型进行试验验证,结果表明所采用的波数域转换方法是可行的,并且相对于重力异常数据,基于重力梯度张量数据的波数域转换结果精度更高。同时,将Vinton盐丘区实测重力梯度张量数据用于波数域转换方法中,得到该地区重力位三阶梯度张量数据,并将所得结果用于DEXP方法的数据解释中,得到该盐丘区的底面深度为533 m,EW向长度为1 350 m,SN向长度为1 125 m,所得结果与前人的研究结果相符合。
致谢:感谢美国Bell Geospace公司提供全张量重力梯度数据。

