自激振荡磁感应传感器研究

张志勇，陈正想，高俊奇

（1.哈尔滨工程大学 青岛创新发展基地，山东 青岛 266300；2.中国船舶集团有限公司第七一〇研究所，湖北 宜昌 443003）

0 引言

磁场传感器广泛用于地磁测量、导航定位、海洋探测及生物医学等领域。根据不同的应用场景，目前市面上已存在各种磁场传感器，例如：感应磁传感器（探测线圈）、霍尔传感器、磁通门传感器、GMI（Giant Magneto Impedance）传感器等，其原理及优缺点可在文献[1]–[8]中找到。

随着数字技术的发展，信息更趋向于以数字形式传输[9-10]，但上述所提及的磁场传感器输出均为模拟信号，即输出信号是电流或电压。要想达到数字形式输出，同时为了减少信号处理过程中的误差，需要使用高性能的模数（A/D）转换器件，这将提高系统的复杂性和成本[11-12]。因此，有必要寻求一种在不使用模数转换模块的前提下，便可实现磁场强度测量的磁场传感器方案。国外PNI 公司提出了磁感应（Magneto-Inductive，MI）技术[13]，应用MI 技术，PNI 公司研制了数字式的磁场传感器以实现磁场测量[14-15]。针对国内数字式磁场传感器的研究，本文提出了一种自激振荡磁感应技术，其测量原理基于励磁电压占空比与被测磁场的线性关系，通过测量占空比从而得到被测磁场强度。这种测量方式不需要模数转换器件，能够减少电路的复杂性和成本。

基于自激振荡磁感应技术，本文研制了一种数字式磁场传感器，并建立了励磁占空比与被测磁场的理论方程，通过实验测试后，验证了自激振荡磁感应技术应用于磁场测量的可行性。

1 系统组成和原理

自激振荡磁感应磁场传感器的原理结构图如图1 所示，其中线圈绕组W与高磁导率的非线性磁芯组成敏感探头，等效电感L、比较器A、采样电阻R3和门限控制电阻R1，R2构成自激振荡电路。电阻R1和R2为比较器电路的阈值设定电阻，采样电阻R3用于将流过线圈的激励电流转换为电压。

图1 磁场传感器原理结构图Fig. 1 Schematic diagram of a magnetic field sensor

传感器工作时，在探头线圈电感、线圈内部磁芯和放大器作用下，比较器输出正向电压为Vo＋，负向电压为Vo-的方波，设置合适的阈值电压V＋，磁芯会进入正负饱和区域。在正负激励电压Vo作用下，非线性磁芯工作在饱和与不饱和状态，由于探头线圈绕组的电感受内部磁芯磁导率影响，其电感在磁芯处于饱和区和线性区时有明显区别。在被测磁场影响下，磁芯提前或延长进入饱和状态，因此在同一振荡周期内，比较器输出方波占空比会增大或减小。

在被测磁场为0 时，磁芯上没有偏置磁场，此时磁芯的磁化曲线如图2（a）中实线所示，磁芯到达正负饱和状态临界磁场相同，在激励电流（图2（c））的作用下，输出电流呈周期对称，如图 2（b）中实线所示，因此在比较器比较输出后，电压Vo正负电压持续时间相同；当被测磁场不为0时，被测磁场与激励电流产生的磁场将叠加在一起，此时磁化曲线将发生偏移，如图 2（a）中虚线所示，磁芯将提前或延长进入饱和区，经比较器后，输出正负电压持续时间不相同，在同一周期内，占空比发生变化。

图2 激励波形下非线性磁芯的工作原理Fig. 2 Operation principle of a nonlinear core under an excitation waveform

综上所述，被测磁场与比较输出电压的占空比存在某种对应关系。因此，只要找到输出电压占空比与被测磁场的关系就能得到被测磁场强度。

2 数学模型

为了找到占空比与被测磁场强度的对应关系，假设磁芯的剩磁和矫顽力足够小，此时磁化曲线可以采用分段近似方法[16-18]。如图 2（a）所示，磁化曲线在线性区和饱和区可以近似为2 段不同斜率的曲线，在线性区内，假设线圈电感为L1，根据基尔霍夫电压定律，可以得到在线性区时输出电压的微分方程为

在饱和区时，假设线圈电感为L2，根据基尔霍夫电压定律，可以得到在饱和区时输出电压的微分方程为

分析图 1 中自激振荡电路，比较器阈值电压为V＋＝R1Vo/(R1＋R2)，采样电阻R3上的电压为V-＝iLR3，当采样电压V-＞V＋时，比较器输出高电平Vo＋，反之，比较器输出低电平Vo-。刚接通电源时，由于探头线圈电感的作用，激励电流iL从0开始增大，当电流增大到使采样电阻R3上电压V-到阈值电压V＋时，激励电压反转，电流将开始减少，如图3 所示。为了使磁芯进入饱和状态，iL应大于饱和临界电流Is，且：

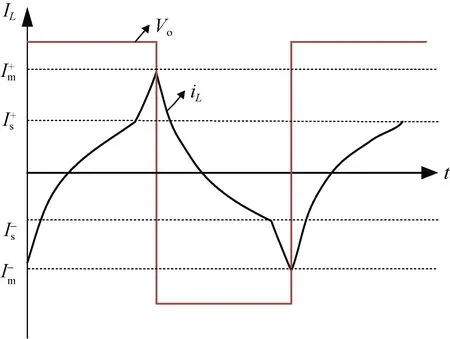
图3 被测磁场为0 时，激励电压和电流波形Fig. 3 Excitation voltage and current waveforms when measured magnetic field is 0

式中：μ为磁导率；N为线圈匝数；Bs为饱和磁感应强度；L为有效磁路长度。

假设被测磁场方向如图1 中所示，在被测磁场作用下，激励电流某时刻处于如图4 所示状态，假设此时被测磁场为B，与激励电流iL产生的交变磁场方向不一致，此时磁芯达到负向饱和所需的电流为Isn-＝-Is-IB（其中IB为被测磁场在线圈上的感应电流，其表达式为IB＝μLB/N）。磁芯达到正向饱和所需的电流为Isn＋＝Is-IB。

图4 被测磁场不为零时，激励电压和电流波形Fig. 4 Excitation voltage and current waveforms when measured magnetic field is not zero

在t= 0 时，磁芯在t1时间段处于负向饱和区，此时，有初始条件iL(0) ＝-Im,iL(t1)＝-Isn-；结合分段线性模型和式（1），可以解得：

式中：时间常数τ2＝L2/(R3＋RL)；RL为线圈内阻；Io＝Vo/(R3＋RL)。

随着电流继续增大，磁芯逐渐进入线性区（4），此时电感从L2变为L1，由iL(t1＋t2)＝-Isn＋，可以解得t2：

式中，时间常数τ1＝L1/(R3＋RL)。

经过t1＋t2时间段后，磁芯再次进入正向饱和区，在时间点t1＋t2＋t3，激励电流iex达到正向电流最大值Im，即iL(t1＋t2＋t3)＝-Im，可以解得t3：

由于磁芯的磁化曲线分段线性模型的对称性，时间段t4、t5、t6可以使用求解t1、t2、t3相同的方法，因此，解得t4、t5、t6如下：

由公式（3）–（8）可以得到负占空比时间Tn和正占空比时间Tp的表达式如下：

实际情况下τ2<<τ1，结合上述求解时间段与理想极限条件下分析，可以得到占空比D和被测磁场B的理论公式：

式中：μ为磁导率；N为线圈匝数；L为有效磁路长度；B为被测磁感应强度；Io为线圈上电流最大值；Is为饱和电流。

从式（11）可以知道，在磁化曲线分段近似的条件下，占空比与被测磁场大小存在线性关系。

基于该测量原理，需要考虑占空比测量精度，目前，测量占空比的方式有很多种，例如使用单片机定时器输入捕获。本文提出的磁场传感器以占空比形式测量更有利于实现数字化。

3 实验结果

基于原理性分析，制作了基于自激振荡磁感应技术的原理样机。磁芯材料性能和研制磁传感器之间有着密切的关系。为了提高磁传感器的测量精度和灵敏度，需要选择低矫顽力、高饱和磁感应强度、低剩余磁感应强度的磁芯材料。因此，本样机中探头内部磁芯采用高磁导率，低矫顽力的钴基非晶合金，磁芯为薄片状，通过骨架固定在线圈中心。将样机放在螺线管中心（在中心处可近似为均匀磁场），如图5 所示。加入不同电流使螺线管内部产生不同大小均匀磁场，记录每组设定磁场下样机输出占空比数据。实验结果如图6、图7所示，由实验波形可以看出，传感器输出波形与理论分析一致。

图5 样机测试图Fig. 5 Prototype test diagram

图6 被测磁场为0 时，输出电压和电流波形Fig. 6 Output voltage and current waveforms when measured magnetic field is 0

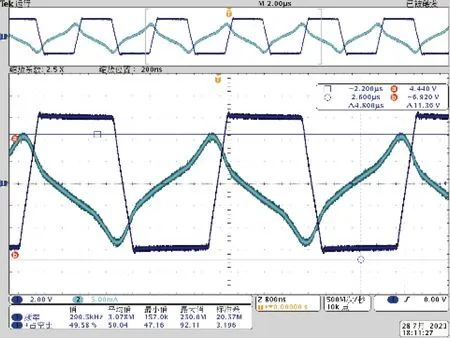
图7 被测磁场不为0 时，输出电压和电流波形Fig. 7 Output voltage and current waveforms when measured magnetic field is not 0

根据测试数据，得到了样机的输出特性曲线如图8 所示。由输出特性曲线可以看出，输出信号处于近似理想的线性工作区。结果表明，在开环条件下，±100 000 nT 量程下传感器的线性度在0.98%。

图8 输出特性曲线Fig. 8 Output characteristic curve

4 结束语

本文提出一种基于自激振荡磁感应技术的新型磁场传感器，该传感器利用了激励电压占空比与被测磁场的对应关系。通过推导理论公式验证了激励电压占空比与被测磁场存在线性关系。与其他磁场传感器相比较，本文提出的磁场传感器模数转换电路等信号调节电路，更有利于实现数字化和小型化。同时，制作了原理样机，并通过实验结果表明了在开环状态下，±100 000 nT 量程下传感器的线性度在0.98%。为后续优化设计自激振荡磁感应传感器有重要意义。