基于BP 神经网络的航磁补偿方法研究
张 宇,陈正想,覃 涛
(1.中国船舶集团有限公司第七一〇研究所,湖北 宜昌 443003;2.国防科技工业弱磁一级计量站,湖北 宜昌 443003)
0 引言
第一次世界大战以来,因人为倾倒、战争遗留等原因遗留了很多水下未爆弹,水下未爆弹危害极大[1],威胁着人民的生命安全以及渔业发展、港口建设等军事和民用领域,因此对水下未爆弹的探测十分必要[2]。
针对水下未爆弹的探测,通常使用磁探测、声探测等方式,其中磁探测相比其它探测方式具有不受空气、水、泥沙等介质影响的优势。相比水下探测,空中探测具有探测效率高的优势,相比有人机平台,无人机平台具有安全性高、成本低、可以低空仿地飞行等优点,因此对于水下未爆弹的探测,基于无人机平台的航磁探测具有重要的意义。
航磁探测通过将磁传感器搭载在无人机上在指定区域飞行来完成,综合精度、体积、重量和稳定性,通常选用光泵和磁通门作为搭载的传感器。目前磁传感器已发展的十分成熟,拥有极高的灵敏度,但是无人机平台本身具有的磁性会干扰传感器的测量,无人机自身的干扰磁场远大于磁传感器的灵敏度,这导致传感器优秀的性能无法发挥出它的作用,因此对无人机平台进行磁干扰补偿十分必要。
根据补偿方式的不同,磁补偿分为硬补偿和软补偿2 种。硬补偿是通过在飞机起飞前进行干扰测量,然后添加等量反向的磁体在飞机上来进行补偿,这种方式耗时长、成本大,因此逐渐被淘汰。软磁补偿通过对飞机干扰磁场进行建模,计算出相对应的补偿系数来计算干扰磁场,是现在常用的补偿方法[3]。
对于航磁补偿的研究从二战时就开始了,当时美军为了满足探潜的需要,将磁通门搭在海军航空兵的飞机上,并进行了一定的补偿。1950 年TOLLES分析了飞机干扰磁场产生的物理原理,将干扰磁场分为固定磁场、感应磁场、涡流磁场3 个部分,并给出了相应的表达式,得到一个具有21 个未知数的线性方程,被称为T-L 方程,为之后的补偿研究奠定了基础。1961 年,Leliak 设计了一套飞行标准来对T-L 方程进行求解;在此基础上,Bickle 设计了一种小信号补偿方法提升了求解的精度;1993年,Williams 提出利用神经网络进行航磁补偿,并建立了以飞机姿态、位置、时间等作为输入的神经网络模型;2014 年,LI 使用信赖域法完成了补偿参数的求解。此外,岭估计法、主成分分析法[4]、改进c-k估计法、截断奇异值分解法[5]、遗传算法[6]、神经网络[7-11]等都被用于补偿参数求解,这些算法的实现,都在不同程度上提高了航磁补偿的精度[12-18]。
针对T-L 模型存在多种假设和近似且补偿参数间存在极大的复共线性的问题,本文采用神经网络建立非线性的干扰补偿模型来进行求解,完成对干扰磁场的补偿,通过仿真和试验对补偿算法进行验证。
1 飞机干扰磁场分析与建模
1.1 干扰磁场组成原理分析
在假设传感器测得的磁场为理想值的情况下,传感器测得的磁场包含期望的磁场,飞机机动性动作产生的磁场、飞机供电设备等产生的电磁干扰。其中,电磁干扰频率较高可以通过低通滤波器滤除,因此研究的重点在如何补偿飞机机动性动作产生的干扰磁场。
Tolles 将飞机机动性动作产生的磁场概括为固定磁场、感应磁场、涡流磁场3 部分。固定磁场来源于飞机平台自身的硬磁材料产生的剩磁,这部分材料磁导率比较低,矫顽力高,它不随时间变化,固定磁场本身是个定值,但它随着飞机姿态的改变,在总场方向的投影也会改变。感应磁场来源于飞机平台的软磁性材料,这部分材料磁导率比较高,矫顽力低,它随着外界磁场的变化改变比较大。涡流磁场由飞机机体对磁感线切割产生,这部分磁场由外界磁场变化的速度决定。
建立飞机坐标系如图1 所示,以飞机的正前方作为T轴,飞机左侧作为L轴,飞机正下方作为V轴建立空间直角坐标系。

图2 磁场关系图Fig. 2 Magnetic field relationship chart
图1 中:Bt表示磁传感器测得的总场;Be表示地磁场;Bi表示飞机产生的干扰磁场;α为总场与T轴的夹角;β为总场与L轴的夹角;γ为总场与V轴的夹角。
设飞机3 个轴向的固定磁场分别为T、L、V,3 个轴之间的软磁系数为TT、TL、TV、VT、VL、VV、LT、LL、LV,3 个轴之间的涡流系数为tt、tl、tv、lt、ll、lv、vt、vl、vv,从而有:
式中:Bperm为固定磁场;Bind为感应磁场;Beddy为涡流磁场;Bt是表示传感器测得的总场;为总场的方向余弦,如式(5)所示;为方向余弦对时间的导数。
由此得到21 项系数的T-L 方程如下:
为了便于计算,将方程投影到总场方向,因为地磁场量级远大于干扰磁场如图 2 所示,因此地磁场方向可以视为与总场方向相同,即其投影值为地磁场自身的标量值,由此转换为标量方程如式(8)所示。
再根据感应磁场的对称性简化得到18 项系数的T-L 方程:
进行简化后得到:
式中:δ为18 个待求解的未知参数;为总场的标量值通过光泵获得;通过磁通门进行计算获得;Be在磁场较为均匀的环境下可以看作是总场的均值。因此方程中未知项为18 个补偿参数,通过求解补偿参数就可以求得飞机的干扰磁场。
1.2 神经网络建模
人工神经网络(Artificial Neural Networks)也简称为神经网络(NN),是根据生物学中神经网络以及网络拓扑知识为理论基础,将人脑结构和外界刺激响应机制进行抽象,模拟人脑的神经系统对复杂信息的处理机制的一种数学模型。
神经网络模型具有并行分布、容错率高、自学习、自适应的优势,在输入充足的节点和合适的模型参数的条件下,就可以对任意非线性函数进行拟合。根据它的这些特点,尝试用它来建立磁干扰补偿模型。经典的神经网络由以下3 个层次组成:输入层(input layer)、隐藏层(hidden layer)、输出层(output layer),如图3 所示,N为输入特征的数量,M为输出特征的数量。

图3 神经网络结构Fig. 3 Neural network structure
神经元是神经网络的基本组成单元,也称为节点或单元,它通过将权重与上一层神经网络的输入的乘积相加并输入激活函数并将结果输出到下一层,单个神经元的结构如图4 所示。图4 中:ijω表示第j个神经元的第i个输入的权重;xi为上一层的输入;yj为下一层的输出;f为激活函数。
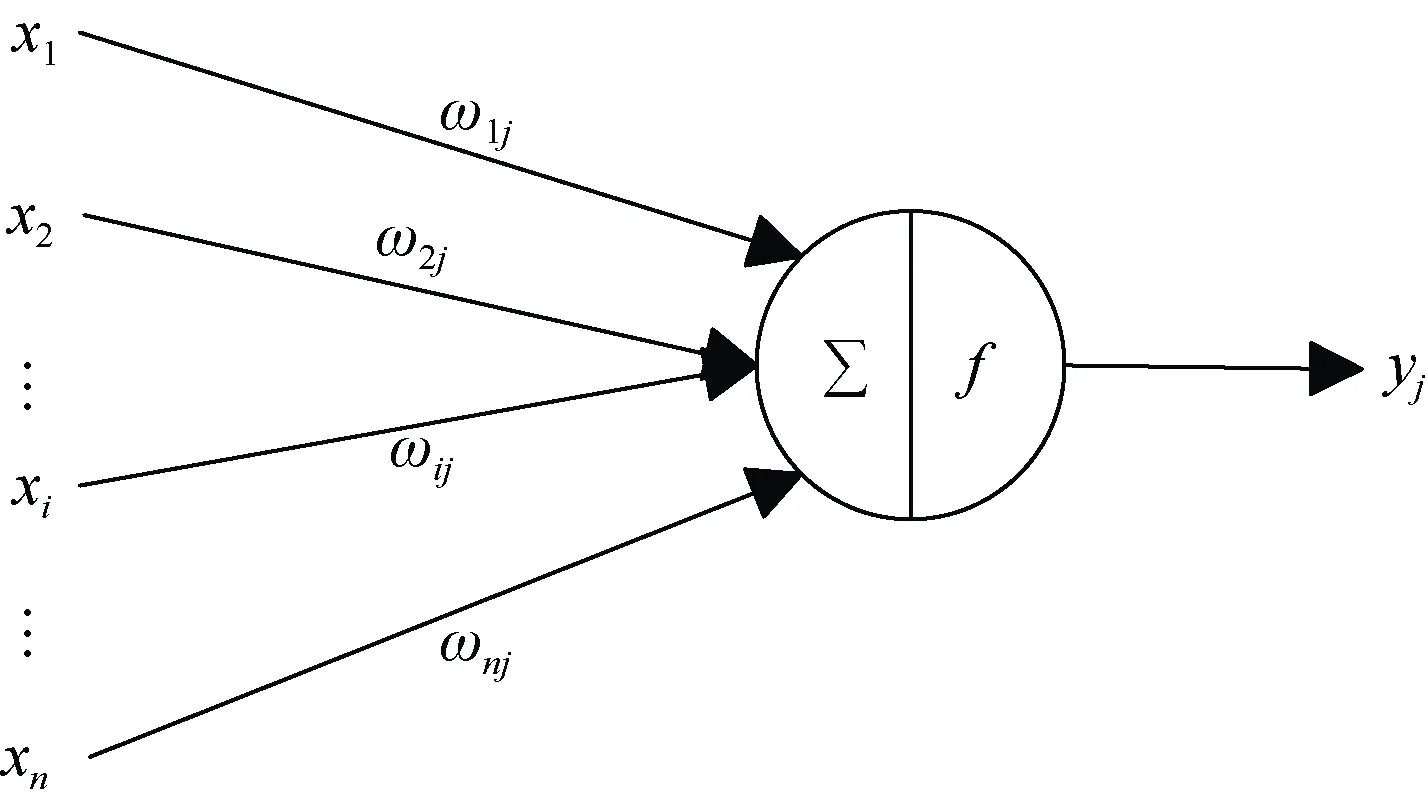
图4 单个神经元结构Fig. 4 Individual neuron structure
常用的激活函数如下,它们的函数图像如图5所示。
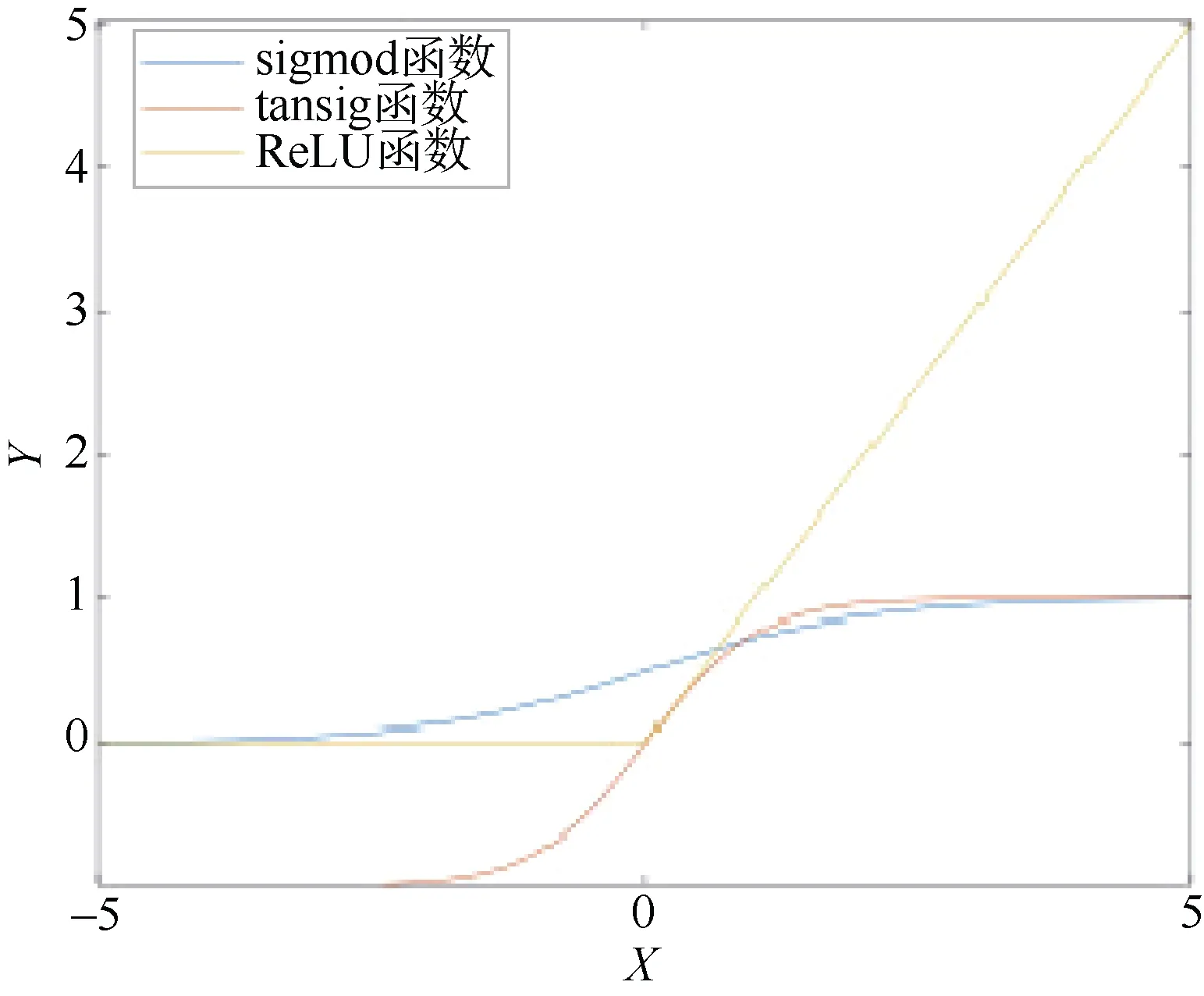
图5 常用的激活函数Fig. 5 Common activation functions
BP(Back Propagation)神经网络是一种误差反向传播的多层神经网络,BP 神经网络可以无需明确输入输出之间的物理联系,通过学习大量的输入和输出的映射关系,求解出其内在数学关系,算法流程如图6 所示。

图6 神经网络算法流程Fig. 6 Neural network algorithm flow
整个算法实现的关键步骤包括:
1)正向传播:
式中:yj为第j个神经元的输出;bj为第j个神经元的偏置。
2)误差计算:
式中:y为实际的输出;d为期望的输出;e为误差。
3)反向传播调整权重:
式中:ρ为学习率,表示权重更新的速度;Δijω为权重的增量。
根据式(10),将A中的18 项参数作为神经网络的输入特征,I作为神经网络的输出,设定单隐层神经网络,神经元个数为3,学习率ρ=0.01,期望误差e=0.01,选取激活函数为tansig (x),建立基于BP 神经网络的航磁补偿模型如图7 所示。

图7 航磁补偿网络Fig. 7 Aeromagnetic compensation network
2 仿真验证
2.1 补偿飞行仿真
设:正北方向与机头顺时针方向的夹角为飞机的航向角,记为φ;磁倾角为I;飞机机轴与水平面夹角为俯仰角记为κ;飞机横轴与水平面夹角为横滚角ω;飞机与航迹的夹角为偏航角,记为θ。
根据以上假设,飞机在不做姿态变换时,与飞机坐标系三轴夹角的方向余弦值可以通过航向角和地磁倾角表示为
飞机只绕T轴做横滚动作的旋转矩阵为
飞机只绕L轴做俯仰动作的旋转矩阵为
飞机只绕V轴做偏航动作的旋转矩阵为
因此可以表示飞机做任意机动性动作时的方向余弦值:
在此基础上,假设补偿系数δ为[–9.9,–2.9,6.5,–7.9 e-5,–2.5 e-5,–9.8 e-5,6.8 e-5,–2.1 e-5,–1.2 e-5,1.7 e-5,–2.3 e-5,–2.9 e-5,–5.8 e-5,–4.4 e-5,–4.7 e-5,1.4 e-5,3.1 e-5,6.2 e-5]。
假设飞机进行四航向飞行,由南向北顺时针进行,在每个航向上进行俯仰、横滚、偏航3 组机动性动作,每个动作做3 次,持续8 s,其中俯仰±5°,横滚±5°,偏航±10°,航迹示意图如图8 所示。
图8 补偿飞行轨迹Fig. 8 Compensated flight path
根据IGRF 模型选取宜昌地区,经度为30°37 ′,纬度为111°18 ′,地磁场强度为50 348 nT,磁倾角I=47°52′,磁偏角D=-4°1 6′,假设区域内地磁场均匀。
设置采样频率为160 Hz,根据式(10)计算得到飞机进行四航向飞行过程中的干扰磁场数据如图9 所示。
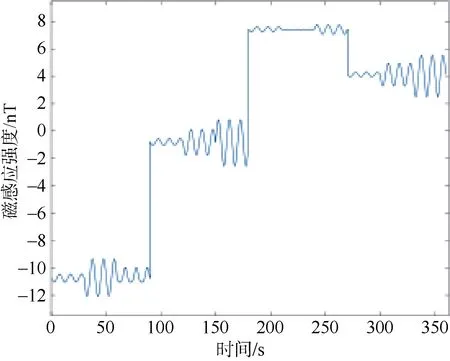
图9 干扰磁场仿真信号Fig. 9 Simulation signals of interfering magnetic field

图10 补偿前后对比Fig. 10 Comparison before and after compensation
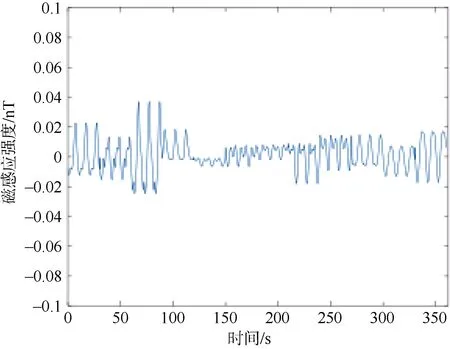
图11 补偿后剩余的干扰磁场Fig. 11 Residual interference magnetic field after compensation
根据假设的地磁场均匀的条件,仿真生成的信号即为式(10)的I,A通过设定的姿态通过计算得到,将A和I输入神经网络模型,并进行补偿得到以下结果。
对于补偿效果的通常采用改善比来评价:
式中:uσ是未补偿信号的标准差;cσ是补偿后信号的标准差。计算出神经网络补偿效果,补偿改善比38.29。
2.2 探测飞行仿真
在对干扰磁场仿真的基础上,添加未爆弹目标信号来仿真探测飞行的过程,从而进一步验证补偿算法。
设置未爆弹口径152 mm,长度1 100 mm,材料30 铬锰硅,假设其位于飞行区域的中心,使用maxwell 仿真未爆弹并添加地磁场得到地磁背景下的未爆弹周围的磁场如图12 所示。
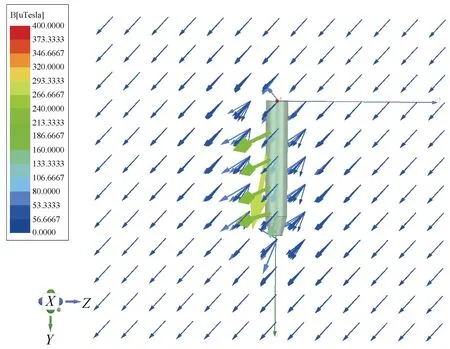
图12 地磁背景下的未爆弹周围磁场Fig. 12 Unexploded ordnance magnetic field in geomagnetic background
设定飞机进行探测飞行时,方向由西向东,与未爆弹目标正横距离为4 m,在图12 中截取出未爆弹磁场正上方4 m 处的磁场,整个平面的磁感应强度如图13 所示。此外假定飞行速度为2 m/s,飞行时间为50 s,采样率为160 Hz,得到探测飞行的期望信号如图14 所示,仿真得到在地磁背景下目标的磁场峰峰值为3.57 nT。
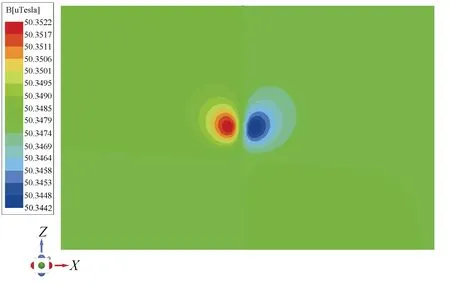
图13 目标上方4 m 处磁感应强度Fig. 13 Magnetic induction strength at 4 m above the target
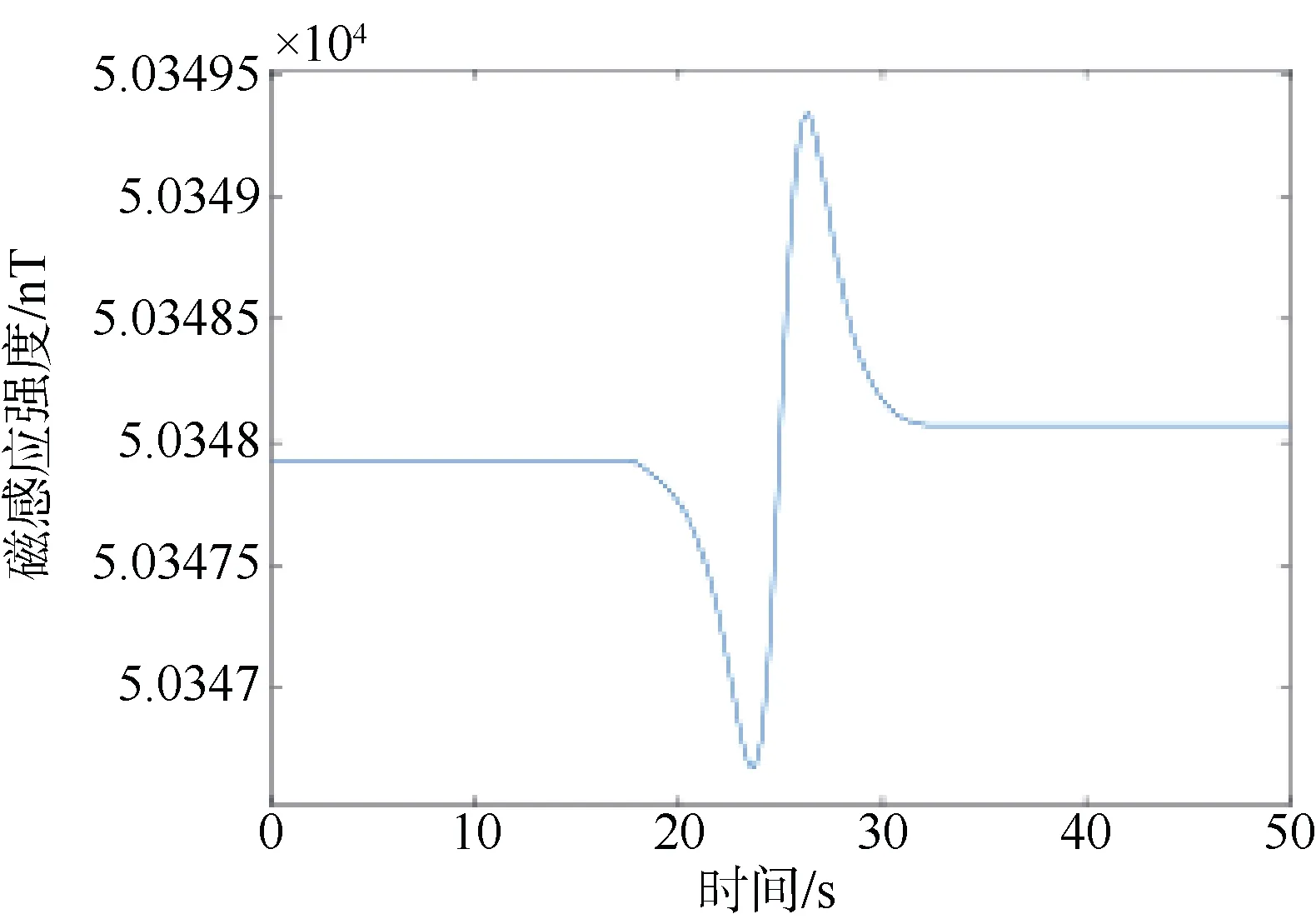
图14 飞机期望的探测信号Fig. 14 Desired detection signals for an aircraft
随机生成15 个姿态并根据采样点数进行3 次样条插值,作为飞机探测飞行过程中的姿态变化,变化范围限制在1°以内,如图15 所示。然后将姿态角代入式(24)计算出探测飞行过程中的干扰磁场,如图 16 所示。
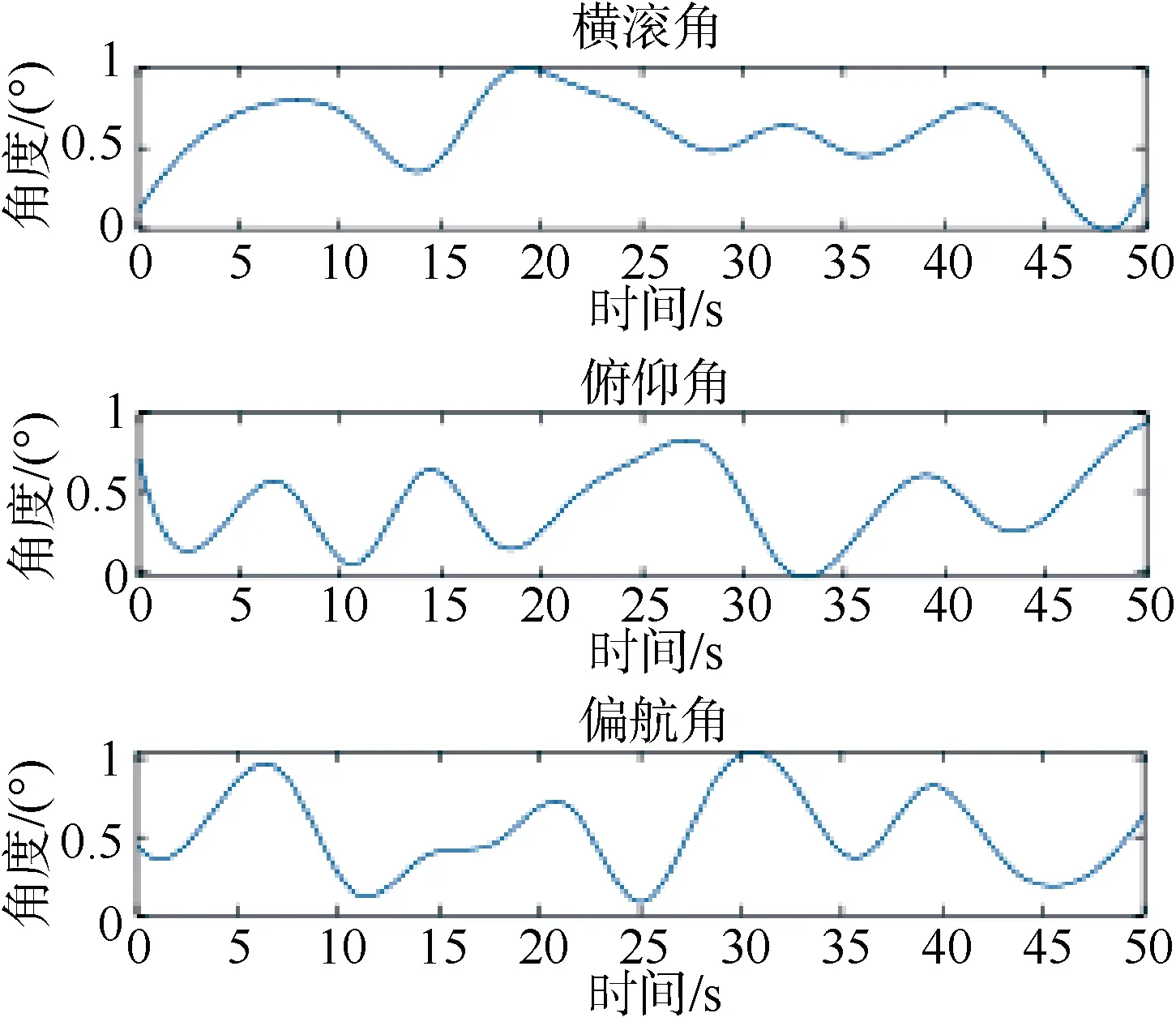
图15 探测飞行中三种姿态角变化Fig. 15 Detection of 3 types of attitude angle changes during flight

图16 探测飞行时的干扰磁场Fig. 16 Interference magnetic field during detection flight
将干扰磁场与未爆弹信号叠加,如图17 所示,可见信号完全淹没在干扰中,将叠加后的信号作为神经网络的输出,姿态角计算出神经网络的输入。补偿后的结果如图18 所示,补偿后信号峰峰值3.46 nT,基本没有衰减,补偿改善比32.08,可以明显发现目标。

图17 叠加干扰后的信号Fig. 17 Signals after overlaying interference
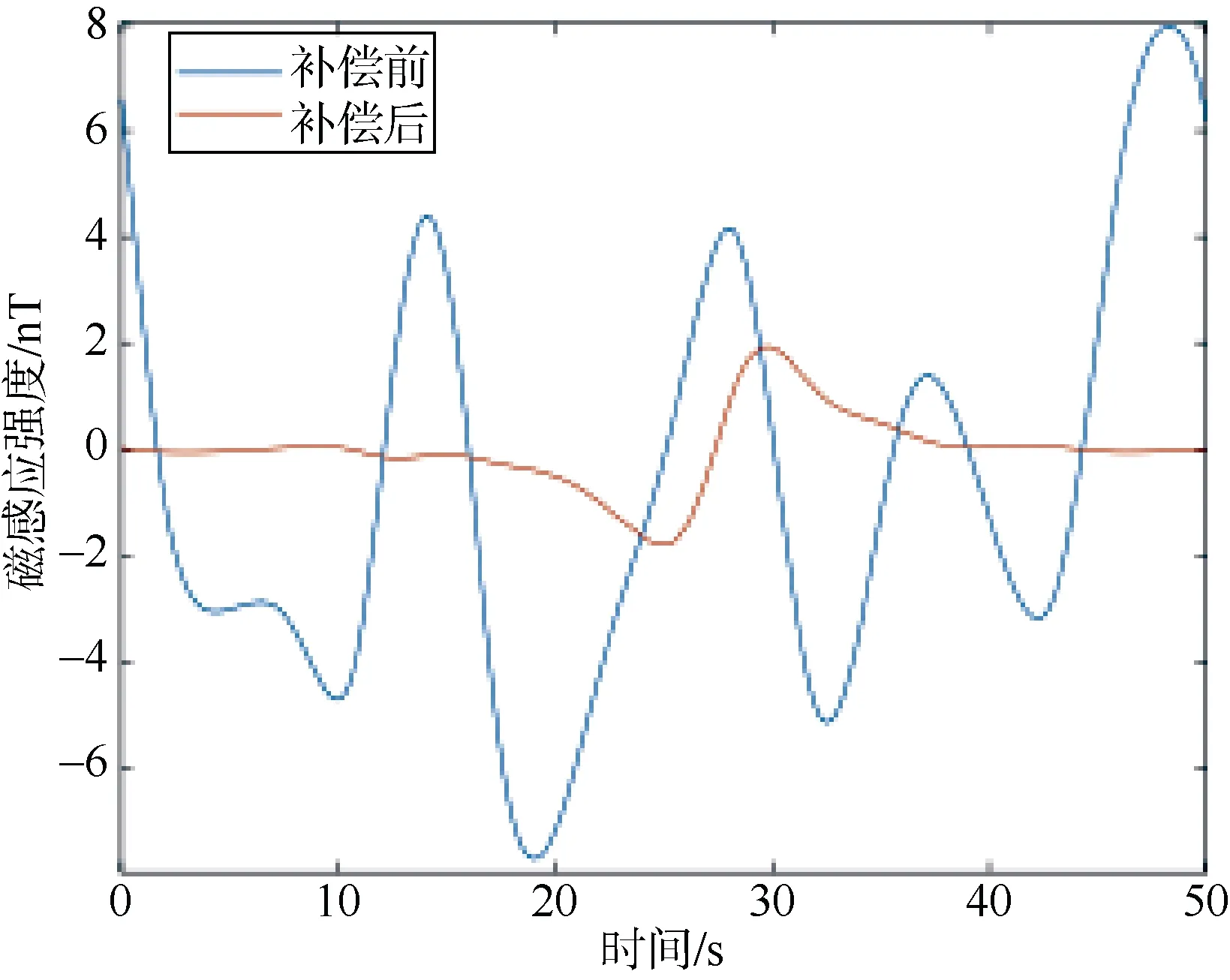
图18 补偿前后对比图Fig. 18 Comparison before and after compensation

图19 实际信号与期望信号对比图Fig. 19 Actual signals and expected signals
3 飞行试验
选择四旋翼无人机平台来进行飞行试验,搭载2 个光泵和1 个磁通门,整个系统如图20。

图20 四旋翼无人机磁探系统Fig. 20 Quadcopter UAV magnetic detection system
由于试验条件限制,且磁场在空气和水中衰减速度近似,试验在陆地进行,选取在宜昌(经度30°37 ′,纬度111°18 ′)附近,分为补偿飞行和探测飞行2 个阶段,与仿真飞行的步骤一致,补偿飞行阶段进行由南向北顺时针四航向飞行,实际目标与仿真目标尺寸相同,探测飞行阶段由西向东离目标正横距离4 m 飞过,目标垂直于地面置于探测航迹正中。
传感器采集到的信号通过滤波消除高频噪声后如图21–22。
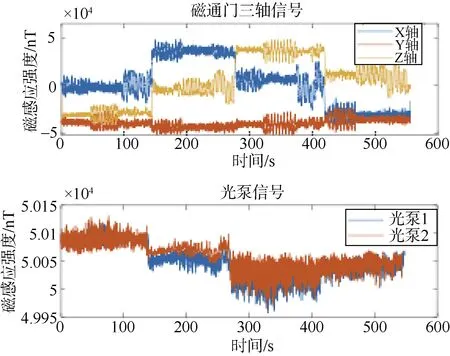
图21 滤波后的补偿学习数据Fig. 21 Compensated learning data after filtering

图22 滤波后的探测飞行的数据Fig. 22 Filtered detection flight data
将单个光泵的信号作为神经网络的输出进行计算,结果如图23–24。

图23 光泵1 补偿效果Fig. 23 Compensation effect of Optical Pump 1
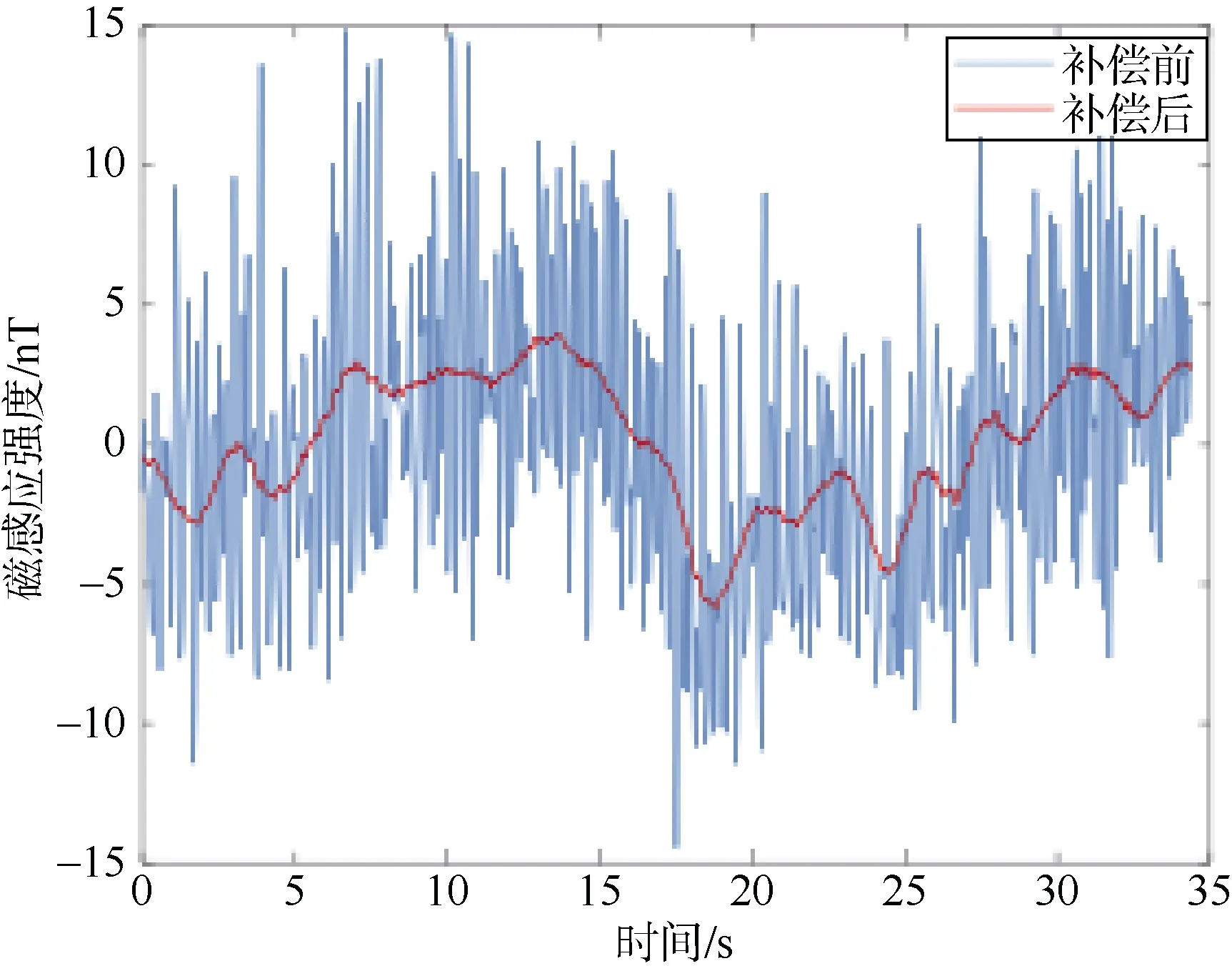
图24 光泵2 补偿效果Fig. 24 Compensation effect of Optical Pump 2
补偿后计算出单光泵改善比为20.57,干扰得到明显抑制。
使用2 个光泵求得的磁场梯度作为神经网络的输出进行计算,补偿结果如图25。
双光泵补偿后,改善比为25.73,信号峰峰值3.2 nT,可以有效分辨目标。
4 结束语
本文利用BP 神经网络搭建了航磁补偿模型实现了对无人机干扰磁场的高精度磁补偿,通过仿真补偿飞行阶段的干扰磁场和探测飞行阶段的干扰磁场以及目标磁场这2 种方式对算法进行了初步验证,在此基础上进行了目标探测飞行试验进一步完成了算法的验证,补偿改善比超过20,试验表明四旋翼无人机平台的航磁补偿方法可以用于提高对水下目标探测的精度。

