新能源车永磁同步电机定子振动分析与结构优化

李民生，黄凯伦，田 锋，赵 坚

（天津城建大学控制与机械工程学院，天津 300384）

为实现“碳达峰、碳中和”的这一重要战略政策目标，国内各大汽车厂商纷纷将目光投向新能源汽车，新能源汽车已经逐渐取代燃油汽车成为人们出行代步的首选.而永磁同步电机具有效率高、响应快、成本低和调速范围宽等众多优越性能[1]，成为了目前新能源汽车驱动最常用的电机类型.永磁同步电机的定子和转子之间有较强的电磁吸引力，其振动主要是由电磁吸引力的径向分量引起的，径向分量会导致定子变形，所以当电机的转子转动时，会直接导致定子的机械振动[2]. 当电磁力的频率与电机固有频率相同或相近时，电机就会发生共振，导致结构变形，使用寿命大大缩短.作为新能源汽车的重要核心部件，电机的平稳安全成为大众关注的焦点，对电机进行振动研究更是对新能源汽车平稳性、安全性评估的重中之重[3].

单夏祺[4]等针对非接触式章动减速电机进行研究，利用Maxwell 有限元软件分析了电机的内部磁场特性.Yang[5]等结合麦克斯韦应力法和洛伦兹力法计算了12 槽14 极永磁同步电机的径向电磁力，并给出了径向电磁力的时空分布图.Li等[6]给出了整数槽多极永磁同步电机的零阶力波的主要来源和频率等特征参数，并提出一种通过增加定转子固有频率和降低电磁力波的谐波含量和振幅的结构优化方法. Zhao[7]等运用子结构模态综合法对永磁同步电机进行计算模态分析，并对其进行结构优化.屈峰等[8]利用模态分析法对电机-减速器总成系统进行研究，得到电机前10 阶模态频率，并通过实验验证了模型的有效性.王大文等[9]采用数值计算的方法对永磁同步电机的运行性能和振动响应进行分析，得到其振动幅值较大的原因是电磁力波与定子固有频率相近引起了共振. 王峰等[10]针对开关磁阻电机进行多物理场仿真分析，研究不同相电机壳体的振动振型.王强等[11]针对某感应推进电机进行谐响应分析，并通过实验验证了结果的有效性.目前，针对新能源车用永磁同步电机定子振动特性的研究较少.

本文针对新能源车用8 极48 槽永磁同步电机定子，利用电磁-结构耦合仿真分析的方法，对其振动特性进行研究，并对其进行结构优化.

1 电机电磁力的计算

永磁同步电机在运行过程中会产生的随时空变化的电磁力，其作为激振力直接作用到定子齿表面导致电机定子产生振动，从而引起整个电机振动.因此，首先要对电磁力进行准确计算.

1.1 电磁力的解析计算

气隙中的磁通密度是由定子的旋转磁场和转子中的磁极相互作用产生的.根据Maxwell 应力方程，永磁同步电机气隙中单位面积受到的径向电磁力可表示为[12]

式中：Pr为径向电磁力；Pt为切向电磁力；Br为径向磁通密度；Bt为切向磁通密度；μ0为真空磁导率；θ 为位置角度；t为时间.

由于径向气隙磁密Br一般远大于切向气隙磁密Bt，故径向电磁力可简化为

当忽略电机铁芯磁路的饱和效应时，电机气隙磁密B可用气隙磁动势与气隙磁导的乘积来确定，即

式中：f（θ，t）为气隙磁动势；λ（θ，t）为气隙磁导.

1.2 电磁力仿真计算

本文研究的新能源车用永磁同步电机为8 极48槽，其主要参数见表1.根据电机的主要参数利用Maxwell电磁仿真软件建立2D 电磁仿真模型如图1 所示.为了保证气隙磁场计算的高精度，在划分网格时，须对定子齿、气隙和转子表面的网格进行细化，剖分结果如图2 所示.

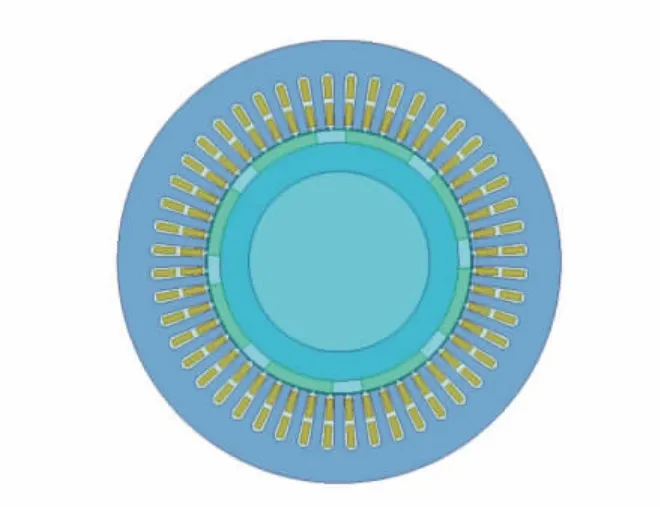
图1 电机2D 电磁仿真模型

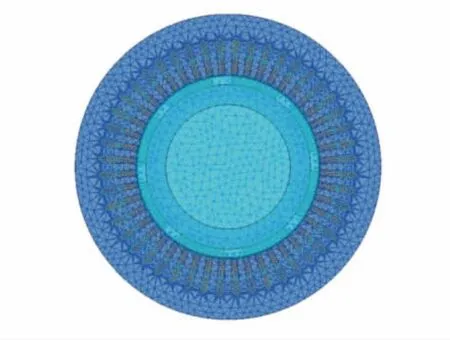
图2 电机2D 有限元剖分模型

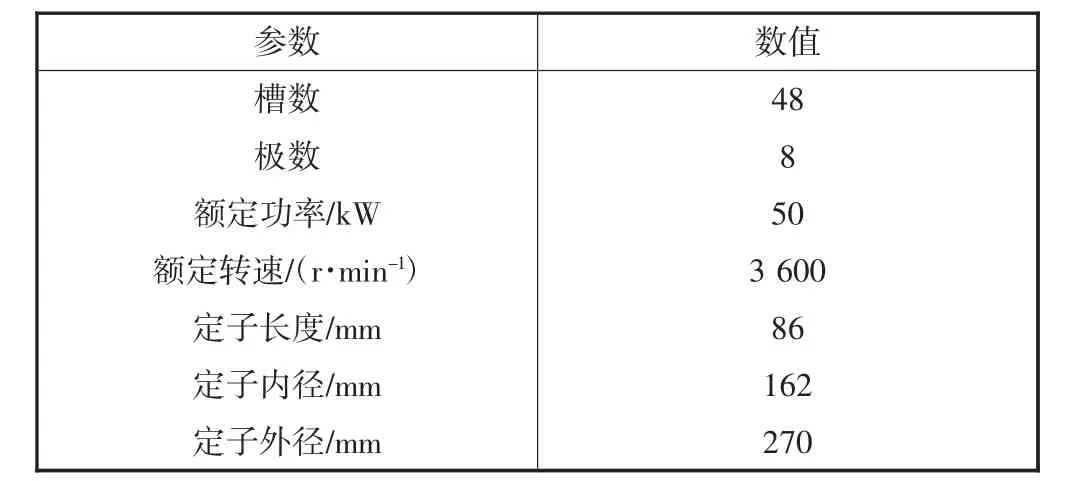
表1 永磁同步电机的主要参数

将永磁同步电机的主要参数代入解析计算式（4）中，利用有限元软件进行求解得到电机在2 m·s 时刻的磁力线（见图3）和磁密云图（见图4）.并通过计算得到电机径向磁密和径向电磁力随空间位置的变化曲线，如图5、图6 所示.

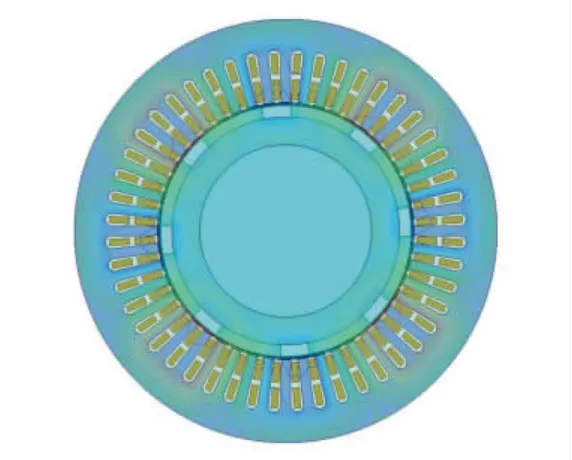
图3 电机磁力线分布

图4 电机磁密云图

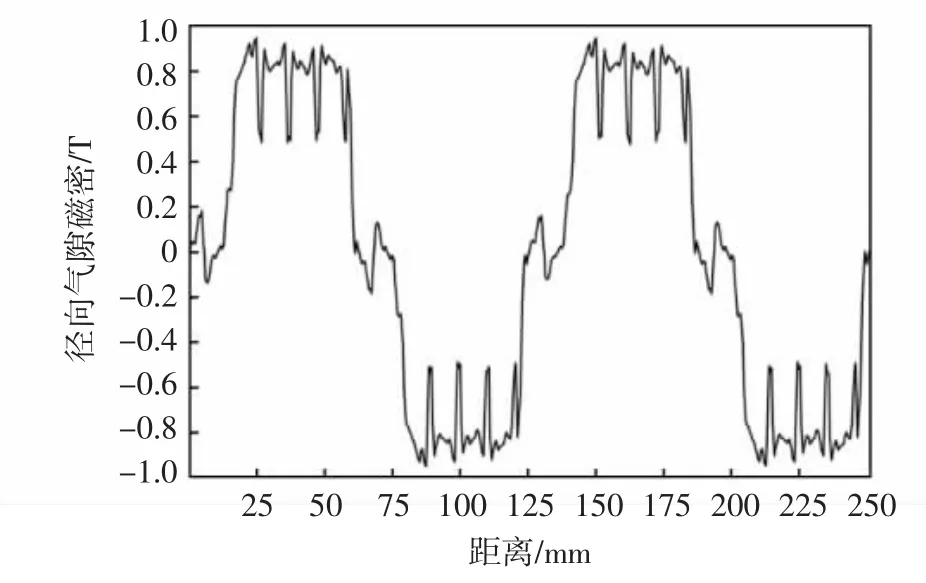
图5 电机径向气隙磁密空间位置分布

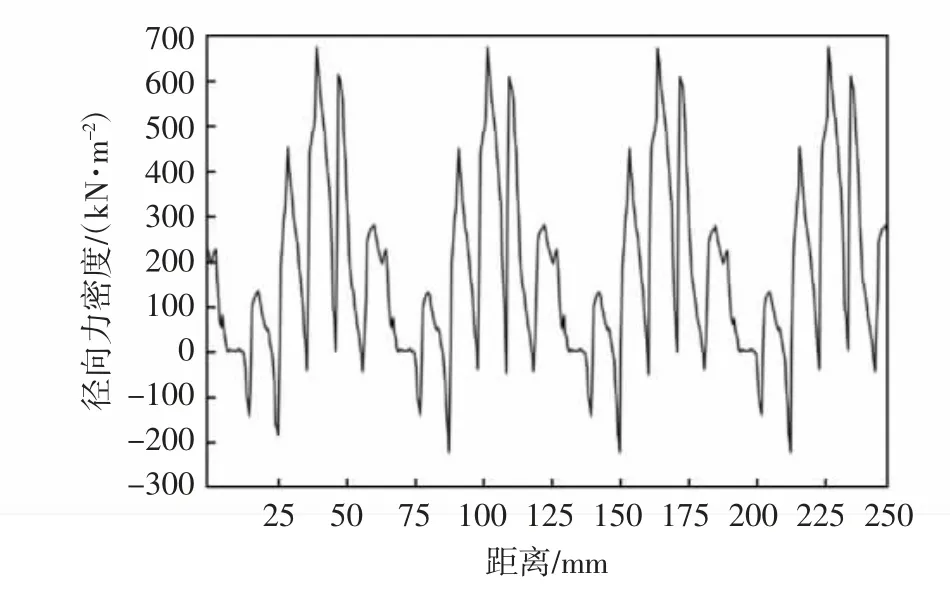
图6 电机径向电磁力空间位置分布

从图4 中可以看出，电机的气隙磁密最大处位于定子齿部.

取电机气隙中靠近定子齿面一点，计算得到电机电磁力密度随时间变化曲线，如图7 所示.对随时间变化的电磁力密度进行二维FFT 分解，得到感兴趣的频率区间0～5 000 Hz 内径向电磁力随频率分布情况，如图8 所示.

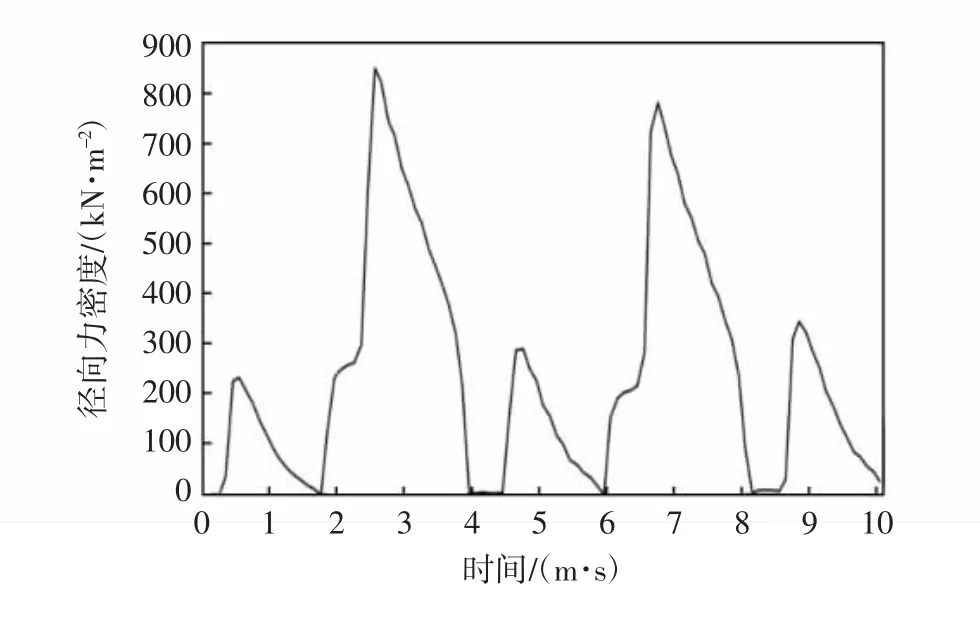
图7 电机电磁力密度随时间分布曲线

2 定子振动特性分析

将计算得到的电磁力与定子进行耦合，通过计算定子的响应加速度，从而分析电机定子在电磁力激励下的振动特性.

2.1 定子3D 建模

根据表1 中电机的基本参数，利用SolidWorks 软件建立电机定子的三维模型，如图9 所示.

图9 电机定子三维实体模型

将电机定子的三维实体模型导入ANSYSWorkbench中，并设置电机定子的材料参数，材料参数如表2 所示.网格划分的质量决定着计算结果的准确性，将定子齿面、齿根及外表面进行网格加密处理，以保证计算结果的准确性，其他设置为默认.生成网格后，查看求解信息得到，电机定子被划分为129 907 个单元，235 163 个节点，网格划分结果如图10 所示.

图10 电机定子网格

表2 材料参数

2.2 定子振动分析

将计算得到的电磁力耦合到电机定子齿面，求解定子在电磁力激励下的振动加速度. 设置分析频率为5 000 Hz，计算定子的振动加速度，得到定子振动加速度随频率变化曲线，如图11 所示.

从图11 中可以看出，定子在受到频率为4 300 Hz的电磁力激励时，振动加速度幅值最大达到2071.6mm/s2.

3 定子模态分析

当定子的模态固有频率与永磁同步电机的工作频率相同或相近时，结构会产生共振，除此之外，当电磁激振力的频率与定子模态固有频率相等或相近时，也会引起结构产生共振.因此，分析电机定子的模态固有频率是十分必要的.

3.1 模态理论分析

模态分析是解决结构振动相关问题的关键，通过模态分析能够得到结构的固有频率与模态振型，这些模态参数只和结构自身的属性有关，如质量、刚度和阻尼[13].根据有限元理论，电机定子的动力学方程可表示为

式中：M为定子质量矩阵；C为阻尼矩阵；K为刚度矩阵；x为节点位移；F为外部激励力.本文研究的电机，阻尼很小，可以忽略不计，可视为n自由度无阻尼的自由振动，其振动方程为

将电机定子的自由振动方程拆解成多个简谐振动的形式，且假设简谐振动的解为

式中：ω 为简谐运动的频率；θ 为任意常数.

将式（7）带入式（6）解得

式中：ω2为特征值；特征向量A为振型.

3.2 定子计算模态分析

计算电机定子的模态固有频率，得到感兴趣的频率范围（0～5 000 Hz）内电机定子的8 阶模态固有频率（见表3），模态振型如图12 所示.

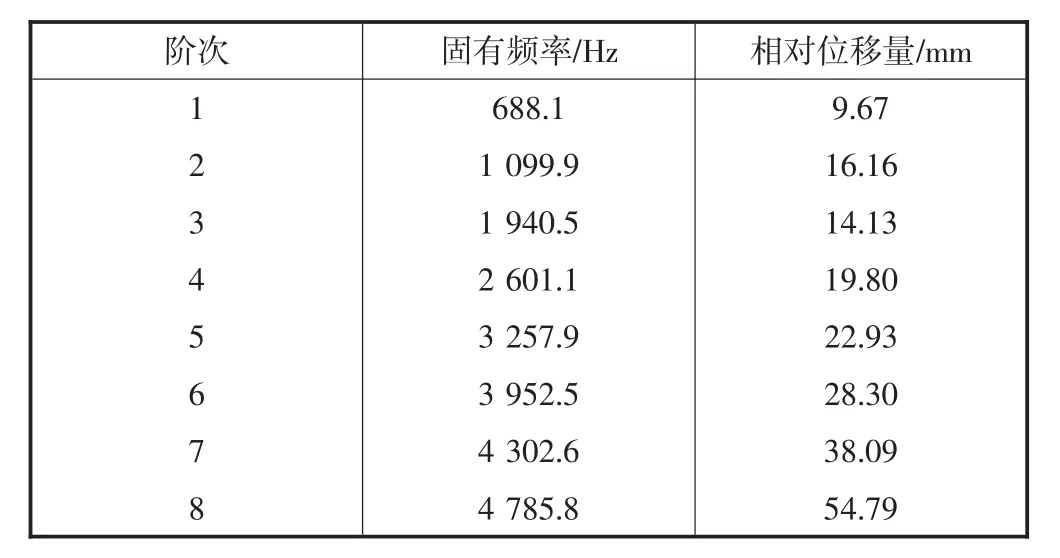
表3 电机定子模态固有频率

结合计算得到的定子模态参数和振型云图可知：固有频率为688.1 Hz，定子呈径向一阶弯曲振动；固有频率为1 099.9 Hz，定子呈径向一阶扭转振动；固有频率为1 940.5 Hz，定子呈径向二阶弯曲振动；固有频率为2 601.1 Hz，定子呈径向二阶扭转振动；固有频率为3 257.9 Hz，定子呈径向三阶弯曲振动；固有频率为3 952.2 Hz，定子呈径向三阶扭转振动；固有频率为4 302.6 Hz，定子呈径向四阶弯曲振动；固有频率为4 785.8 Hz，定子呈径向五阶弯曲振动.

对比图11 和表3，发现定子振动幅值在激励频率为4 300 Hz 时出现最大值，分析其原因是由于电磁力激励频率与定子的第7 阶模态（见图12 g）频率相近，故引起定子强烈共振.因此，有必要对电机定子进行结构优化从而减小振动.

4 电机定子结构优化

定子电磁力频率和模态频率避开有两种方法：一种是改变径向电磁力频率；另一种是改变定子结构的模态频率.由于径向电磁力频率与电机通入的电流、转速、和电机性能有关，改变的难度较大，因此，本文选择改变定子结构的模态频率.

基于以上分析，本文采取减小定子质量的方式，并提出三种定子优化方案：优化模型a 将原定子外圆周均匀加工6 个梯形槽，如图13 所示；优化模型b 将原定子外圆周均匀加工6 个弧形槽，如图14 所示；优化模型c 将原定子外圆周均匀加工6 个平面，如图15所示.

图13 优化模型a

图14 优化模型b

图15 优化模型c

将优化后的三种定子模型重新导入ANSYS Workbench 中，定义材料和单元类型，将相同的电磁力耦合到优化后的定子齿面，进行振动特性分析，计算定子的振动加速度.原始模型和三种优化模型的振动加速度变化曲线如图16 所示，三种优化模型的最大振动加速度幅值和相对变化量见表4.

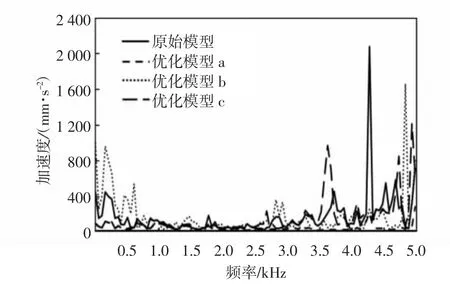
图16 优化前后定子振动加速度随频率变化曲线

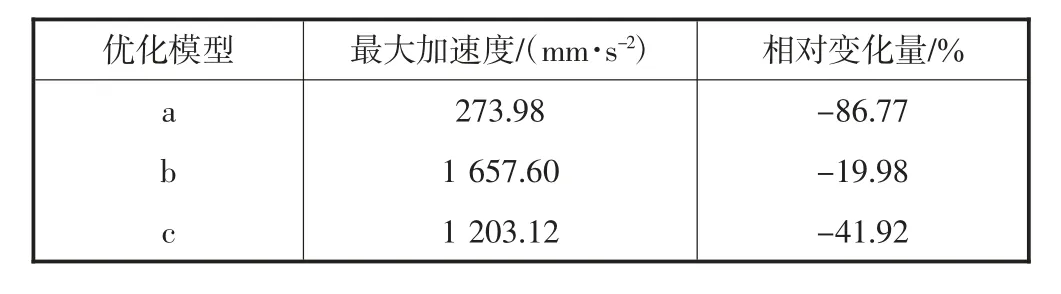
表4 定子优化后各模型的最大振动加速度及相对变化

从图16 可以看出，三种定子优化模型的振动加速度最大值均有不同程度的减小，优化模型a 的振动加速度幅值比其他两种优化模型整体上减小更明显.由表4 可以看出，优化模型a 最大振动加速度幅值由原来的2 071.6 mm/s2减小到273.98 mm/s2，减小了86.77%；优化模型b 最大振动加速度幅值由原来的2 071.6 mm/s2减小到1 657.60 mm/s2，减小了19.98%；优化模型c 最大振动加速度幅值由原来的2 071.6 mm/s2减小到1 203.12 mm/s2，减小了41.92%.

5 结 论

（1）分析新能源车用永磁同步电机定子的振动问题，采用电磁-结构耦合仿真的方法，能够准确计算出电磁力随时间和空间的变化曲线，得到电机定子在受到不同频率激励时的振动情况.

（2）定子在激励频率为4 300 Hz 的电磁力作用下振动幅值最大.对电机定子进行计算模态分析，得到8阶模态频率，发现引起电机定子产生最大振动加速度的激励频率恰好与定子的4 302.6 Hz 固有频率相近，导致其产生强烈共振.

（3）提出三种电机定子结构优化方案. 三种方案均能够使定子的最大振动加速度幅值减小，但优化模型a 的优化效果更好，最大振动幅值减小了86.77%，分析结果为下一步优化电机振动噪声提供了可靠数据.