基于回波模型仿真的ADCP实验室校准中波束间干扰研究

刘建遥, 焦君圣, 郭世旭, 张纪炜

(中国计量大学 计量测试工程学院，浙江 杭州 310018)

1 引 言

声学多普勒流速剖面仪(acoustic Doppler current profiler,ADCP)是一种新型流速测量仪器,其工作原理为应用多普勒效应,能测量包括流速在内的船速、水深、水温等多项海洋环境[1]。因其测量精度高、测量范围广、测量时对流场无影响等优点,而被广泛应用于水下导航、水利监测、海洋观测等领域[2]。

ADCP作为测量仪器,需对其进行定期的检定校准[3]。目前ADCP校准存在水域校准和无水域校准两条技术路线[4～6]。以往对ADCP的校准是在大深度的开阔水域中通过实物船只进行校准实验[7～9],其对水域环境要求严格,并且成本不菲;现今Strathclyde大学的开尔文流体力学实验室通过建设大型水槽,并使用拖车产生速度和螺旋桨产生水流用于ADCP单波束校准[10],实验结果表明精度不受拖车速度的影响;杨枭杰等开发了一套ADCP单波束校准系统[11],其通过应答器阵列回发频偏信号能实现ADCP现场校准;马龙等研究了一种校准ADCP的声学仿真方法,通过对接阵回发仿真信号实现对ADCP的实验室环境下无水域校准[12],由于其使用的是理想的仿真信号,与实际情况存在些许偏差,使得校准不全面。以上校准方式在校准成本、校准效率以及完整性上皆存在一些不足。

本文针对上述问题建立了一种较为真实的ADCP仿真回波模型,并根据模型提出一种ADCP实验室水池环境下多个波束同时校准方式,针对该方式可能出现的波束间干扰问题,利用仿真模型对不同类型的ADCP进行干扰探究。

2 底跟踪回波模型

基于射线声学的假设,声源发射的声波以波束形式在海洋中传播,声波投射到海底后与散射物质发生散射形成散射回波,并在接收声呐处叠加形成混响,这就是ADCP的底回波[13]。

海底环境对于底回波的贡献集中在两个方面,一个是海底的粗糙界面所造成的界面散射,另一个是海底沉积物的非均匀性引起的体积散射。Jackson模型是一种应用了复合粗糙度模型的高频海底声散射模型,包含散射强度、入射声波频率、声波掠射角、海底环境等一系列参数,能对各种海底环境进行建模分析[14]。如图1所示为海底散射示意图。

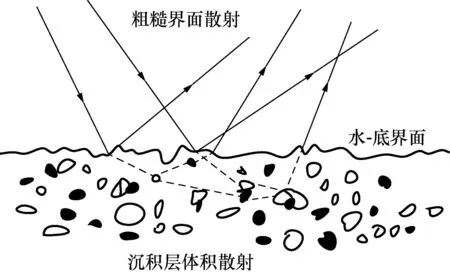
图1 海底散射示意图

通常使用散射截面的分贝形式来定义海底散射强度Sb,Jackson模型的散射强度计算公式为:

Sb=10lg(σSSA+σv)

(1)

式中:σSSA为海底粗糙界面散射引起的散射截面;σv为海底沉积物体积散射引起的散射截面[15]。

2.1 粗糙界面散射

在Jackson模型的发展中,基尔霍夫近似和微扰理论一直是研究粗糙海底界面散射的主要方向[16]。但近些年小斜率近似法(small slope approximation,SSA)发展较为迅速,其囊括了基尔霍夫近似和微扰理论,并在适当的边界粗糙度范围内减少每一次近似,弥补了两种经典近似之间的差距[17]。故本文采取SSA模型对粗糙界面散射进行计算。

在高频状态下,最低阶小斜率近似模型的粗糙海底界面散射截面为[18]:

(2)

式中:

(3)

(4)

(5)

式中:ki和ks分别是入射波和散射波矢量,两者之间的水平波矢量差Δk称为Bragg波矢量,定义如下:

Δk=ki-ks

(6)

ki=kw(excosθi-ezsinθi)

(7)

ks=kw(excosθscosφs+eycosθssinφs+ezsinθs)

(8)

式中:kw为水中的声波数;式(3)中C(x)为在零滞后条件下单位归一化的表面粗糙度相关函数;h表示的是均方根起伏(RMS),其意义为海底起伏与平均沉积物-水界面的均方偏差,表示如下:

(9)

式中:ω2为海底界面起伏谱强度;γ2为海底界面起伏谱指数;Lr为截止长度。式(5)中W(K)是海底粗糙度的二维高度谱密度,符合“幂律”拟合形式。

(10)

式中:K表示二维矢量波数[19]。

2.2 沉积层体积散射

沉积层体积散射是由于沉积层中内部介质的不均匀性引起声速和密度的随机起伏,进而导致体积散射。在沉积层中,声压符合Helmholz方程,根据 Born 近似求得其远场解,得到其沉积层体积散射截面如下[20]:

(11)

式中:

(13)

Δ=cos2θi+cos2θs-2cosθicosθs

(14)

式中:γ3为海底沉积物不均匀性谱指数;ω3为海底沉积物不均匀性谱强度;ρ为沉积物与海水密度比;μ为海底沉积物中密度扰动的压缩比。κ为沉积层中的声波复数波与海水中声波实数波之比,其定义如下:

(15)

式中:ν为沉积物中声速与海水中声速比值;δ为损失参数,定义为沉积层中声波虚波数和实波数之比,定义如下:

(16)

式中:αb是沉积物的吸声系数[21]。同时在式(11)中定义了如下两个表达式:

(17)

(18)

R(θ)定义为声波通过流体-流体介质中的Rayleigh反射系数。

3 底跟踪模型建立

ADCP发射的声波照射到海底所形成的区域是一个椭圆形,任一时刻对混响有贡献的散射体都存在于一个圆环内,并且圆环随着时间外移。设定不考虑发射波束旁瓣的影响。示意图如图2所示。

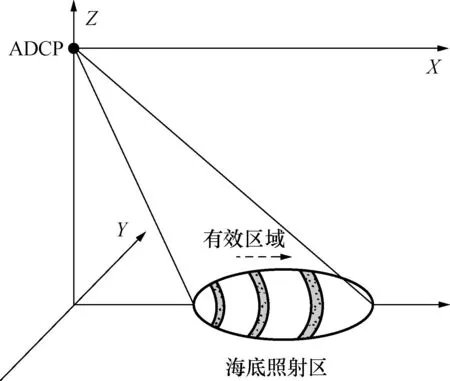
图2 ADCP海底散射模型

假设散射体出现在海底任意位置的概率相同,则任意面积单元内的散射体数量符合泊松分布:

(19)

式中:Δr表示面积单元大小,泊松分布的均值λ为:

(20)

式中:ρ(r)为Δr区域内散射体数量。故只需设定一个平均散射体密度,就能得出各个面积单元内的散射体数量。

模型根据散射体数量选择单元散射和点散射计算,当某一时刻内有效散射体的数量超过阈值,则认为其满足中心极限定理[22],采用单元散射模型,反之选用点散射模型。

本文采用射线理论建立传播模型,设定后向散射回波过程是一个线性时不变系统,并且ADCP存在一定的速度。则底回波模型为:

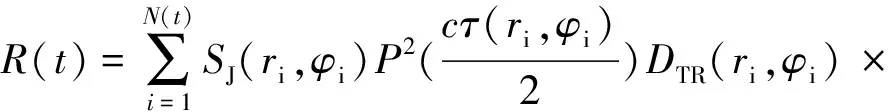
X(kd(t-τ(ri,φi)))ej[ω0τ(ri,φi)+φi]

(21)

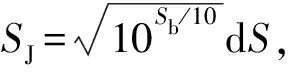
(22)

式中:a为吸收系数(dB/m),根据Thorp[24]给出的表达式为:

(23)

式中:f为信号的频率。式(21)中DTR是换能器的波束图;X(t)为发射信号的复包络;φi为混响的随机相位,服从[0～2π]之间的均匀分布;τ为声波传播延时;ω0为发射信号的载波中心频率。kd为时间尺度压缩因子,其值为:

(24)

其含义是多普勒频偏,经过解算可得速度信息。

4 水层跟踪回波模型

声波在水中传播时,水体中存在很多悬浮的散射物质(如浮游生物、颗粒、气泡等),其随着水流一起运动,两者速度相同。在散射物质作用下,将产生各个水层的混响信号并共同作用于接收声呐处,此为ADCP的水层回波。

当ADCP换能器向下发射信号时,不同深度水流所携带的速度信息是不一样的,所以需要对其进行分层测流。通过对回波信号进行时空特性分析,可以得出如图3所示的时空传播模型。

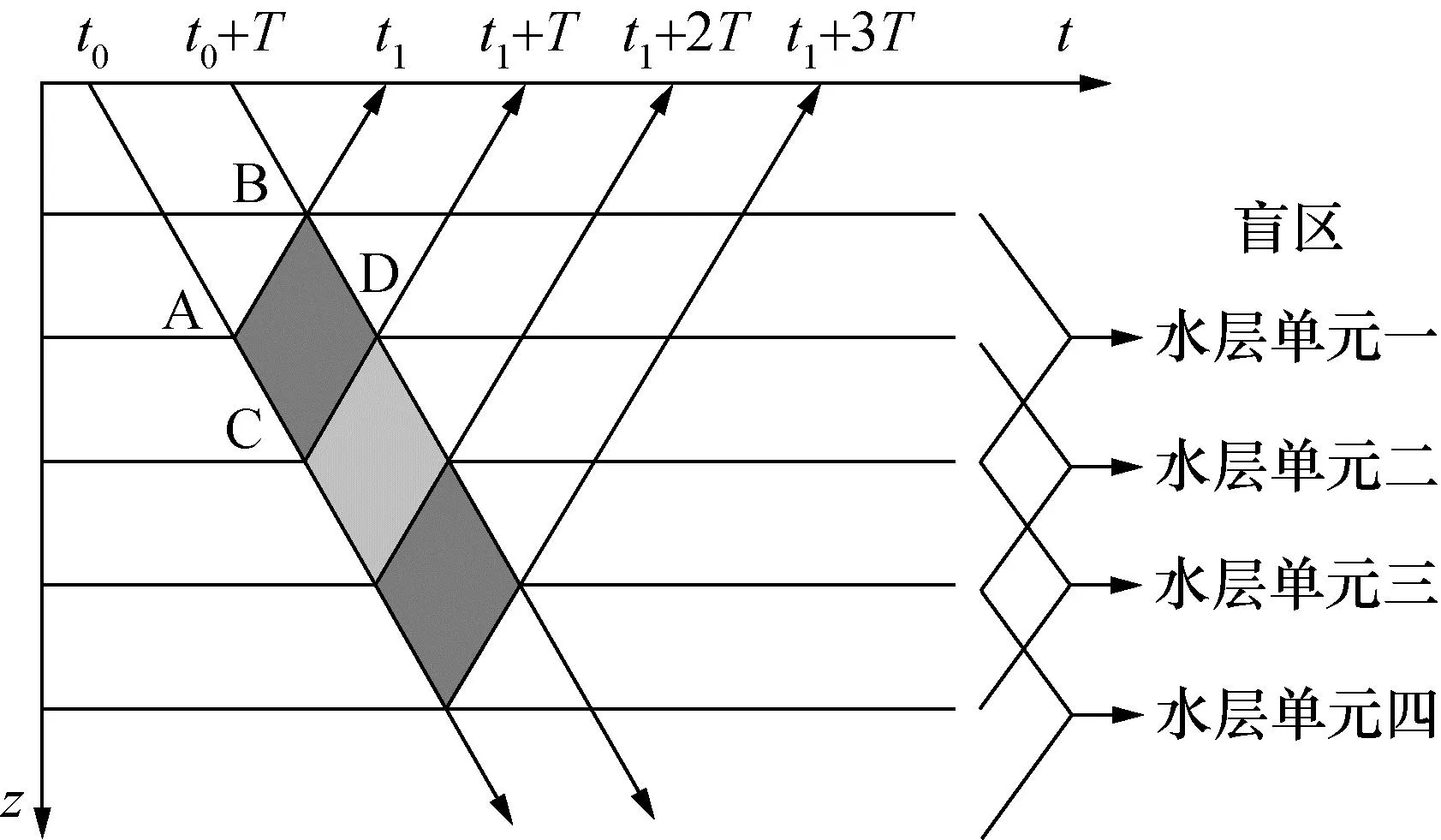
图3 ADCP水层回波时空模型

假设ADCP在t0时刻开始发射声脉冲前沿,t0+T时刻发射脉冲后沿,T为脉冲长度。声波在水中传播经过盲区后,脉冲前沿到达A处形成后向散射回波,该回波到达B处时与脉冲后沿在此处形成的回波叠加后被ADCP在t1所接收。同理在t1+T时刻接收到的信号是C和D处的散射回波。则在时间窗T内,所有有贡献的散射体位于ABCD区域内,此即为一个水层单元。由以上分析可知,某一时间窗的回波由其主体的水层以及相邻水层内散射体的后向散射回波混叠而成。中间位置的贡献最大,越到两端,贡献越小。

ADCP发射的声波存在发射角度φ和波束立体角θ,所以其照射的区域是一个斜圆锥体,某一时间窗内有效区域是一个倾斜的圆台。为了简化计算,本文选择一种近似模型,即将圆台的上下椭圆面进行掠射角方向旋转[25],得到一个圆面,并将圆面进行下凹成球面,至此将斜圆台转换为下凹圆台,下凹圆台内各球面距ADCP距离相等。示意图如图4所示,旋转会造成部分区域的散射体被忽略以及其他水层的散射体被涉及,但是区域处于边界附近,所占比例较少,影响较为微弱。

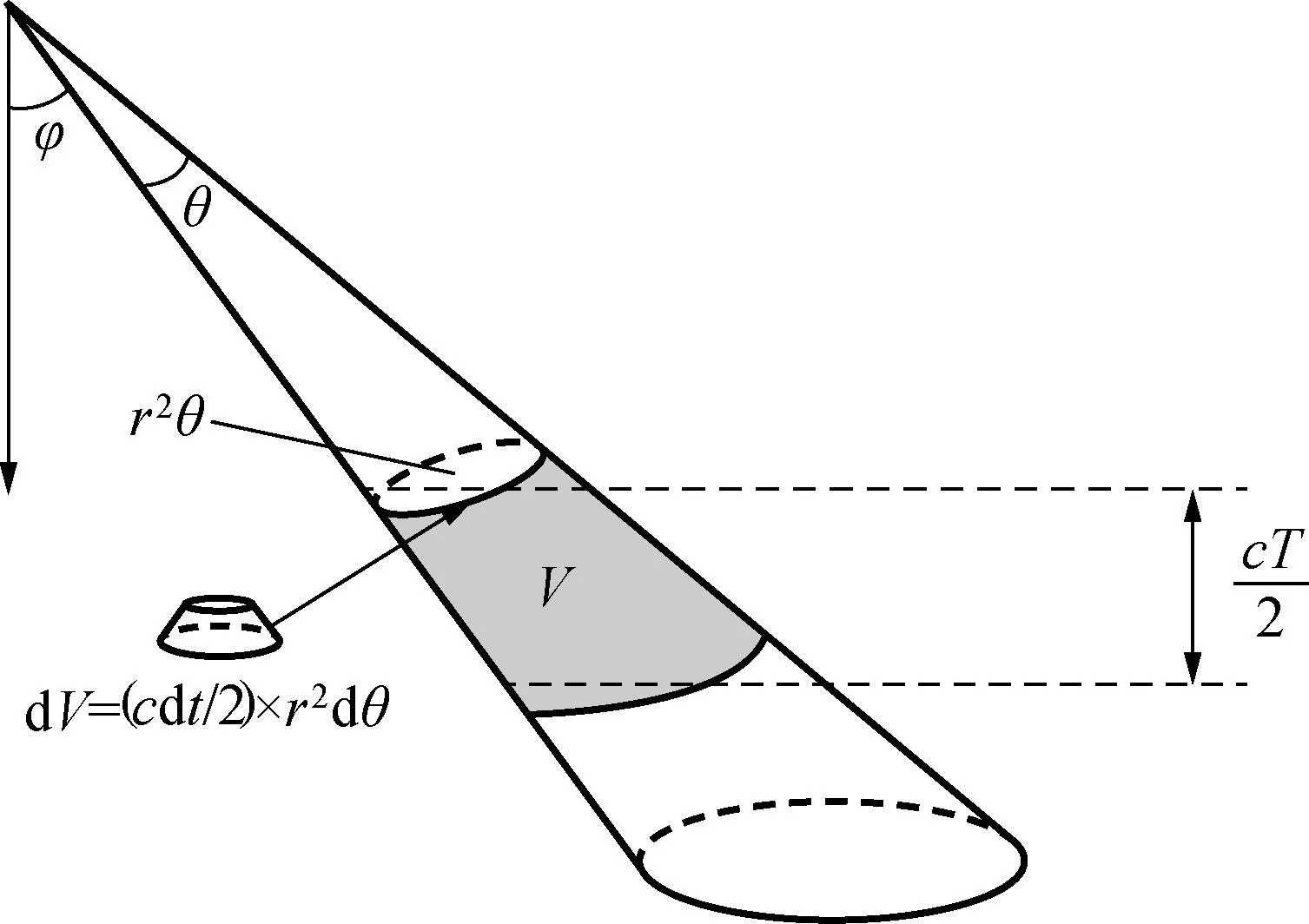
图4 ADCP水层回波模型

根据上述体积散射回波模型,某一水层回波信号可以表示为:

X(kd(t-τ(ri,φi))+φi/ω0)

(25)

5 回波模型实验验证

根据所建立的ADCP回波模型,在浙江千岛湖进行湖试实验验证模型准确性,实验水深约 52 m,ADCP固定在静止船的船头,入水3 m向下发射声波,对底对流测量精度为:±0.5%V±0.005 m/s。模型参数与实验参数一致,载波频率614.4 kHz,宽带信号为5阶m序列编码,码片宽度0.009 7 ms,重复次数19次,仿真环境选取一组典型的海底环境参数[26]。分别对比回波模型和实验的时域信号和统计特性。图5所示为底回波仿真和实验的结果。

图5 SSA仿真模型和湖试底回波时域图

可以看出,两者在时域的波形上存在极大的相似性,并且在图6的统计规律上,仿真和实验的结果在瞬时值和包络的概率密度分布上遵循高斯分布和瑞利分布,其中拟合的瑞利分布曲线的分布模型参数为0.26。

图6 SSA仿真模型和湖试底回波统计特性

另外对底回波模型进行50次重复性试验,以检验模型的速度误差和方差。

图7为对底回波模型进行重复性试验得出的底跟踪各速度点平均误差和方差,结果为误差和方差都比较小,模型稳定性较高。同理,对水层回波选取某一水层进行验证,水层回波模型进行100次重复性试验。如图8所示为水层回波仿真与实验的时域对比图,两者一致性较高。图9表明,瞬时值和包络都满足相应的统计规律,其中拟合的瑞利分布曲线的分布模型参数为0.22。图10为水层回波重复性实验的流速平均误差和方差,误差较小且稳定性较高。综合以上验证分析,建立的海底和水层回波模型都符合要求。

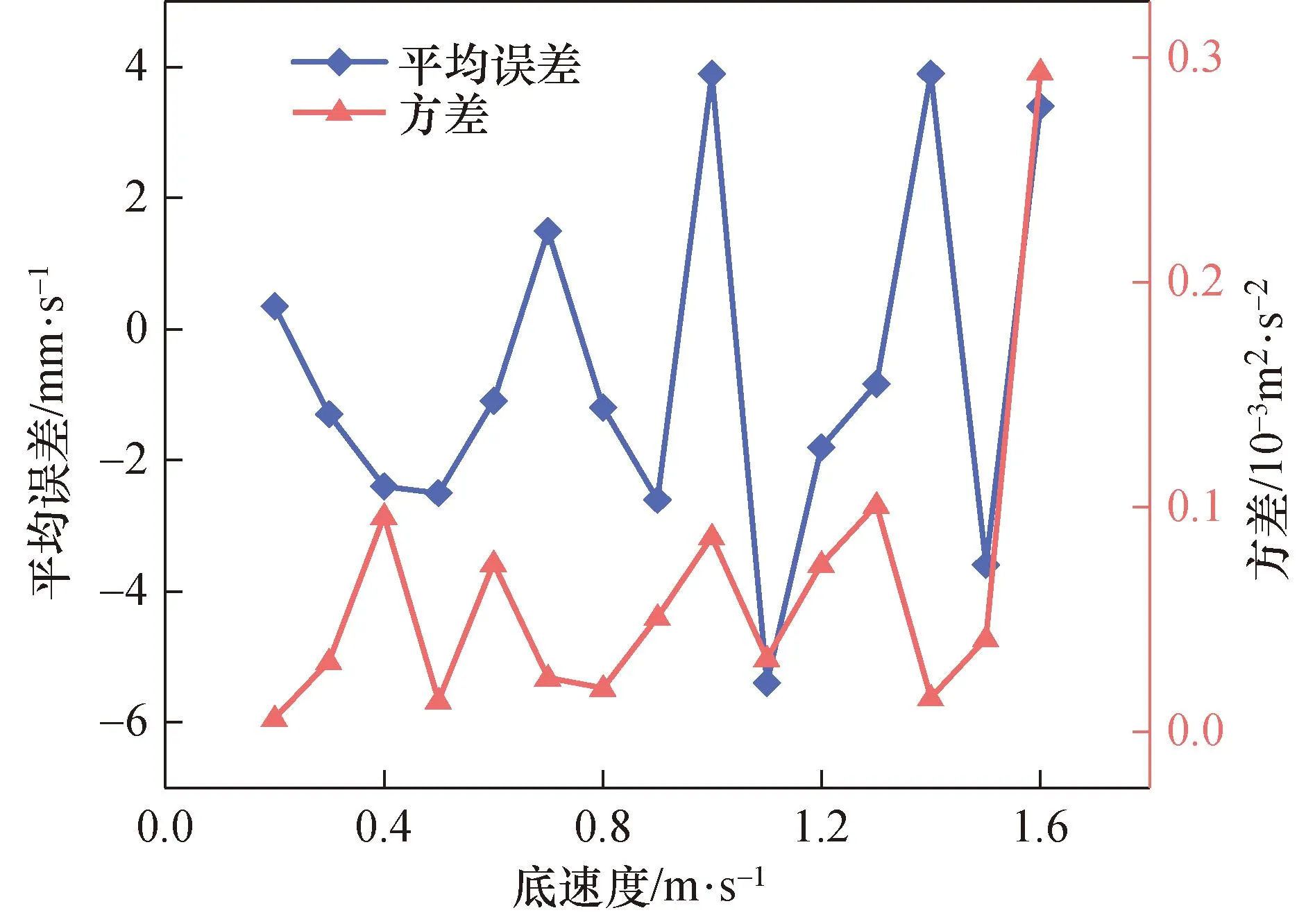
图7 底回波速度误差及方差

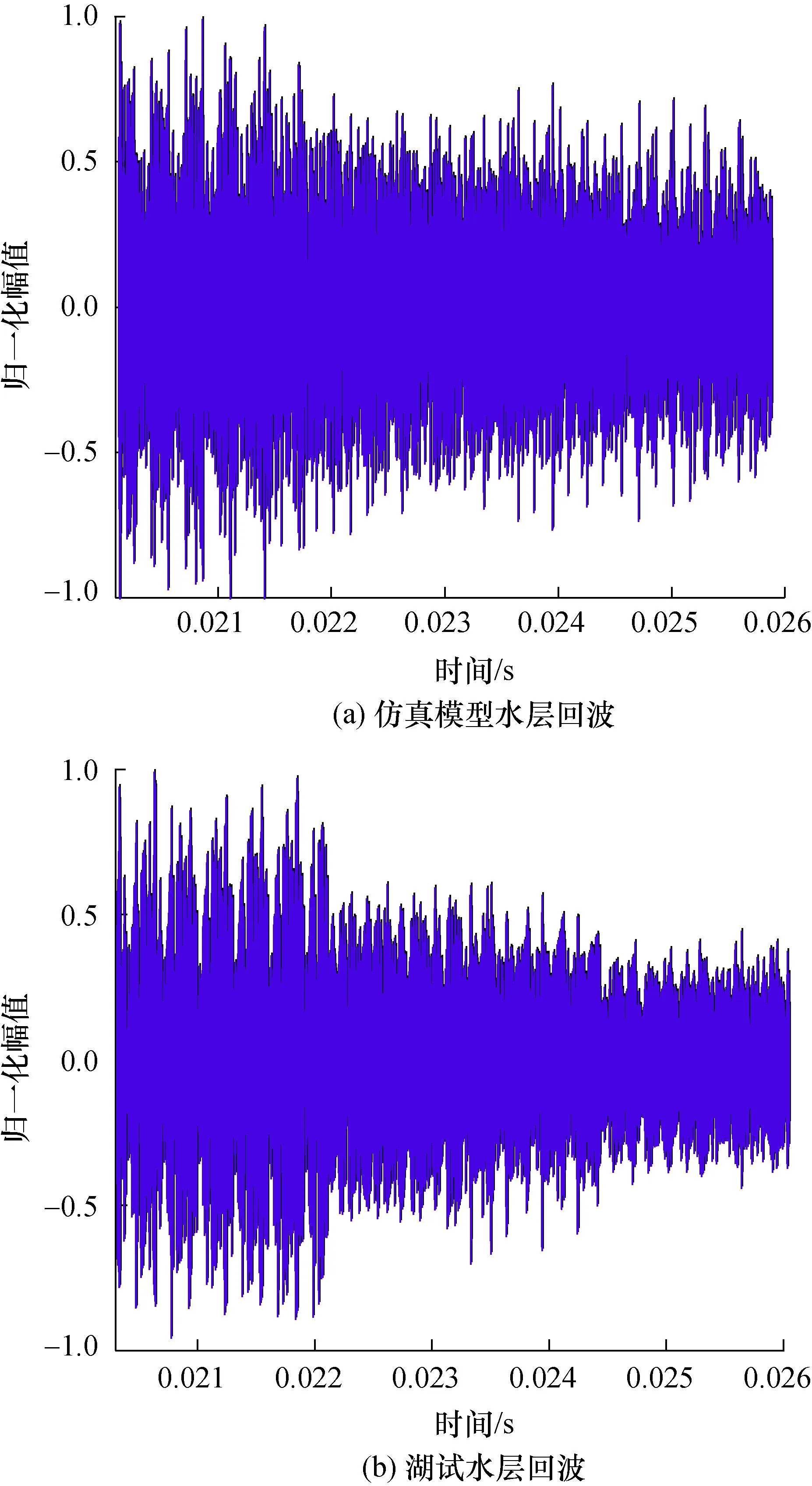
图8 水层仿真模型和湖试水层回波时域图

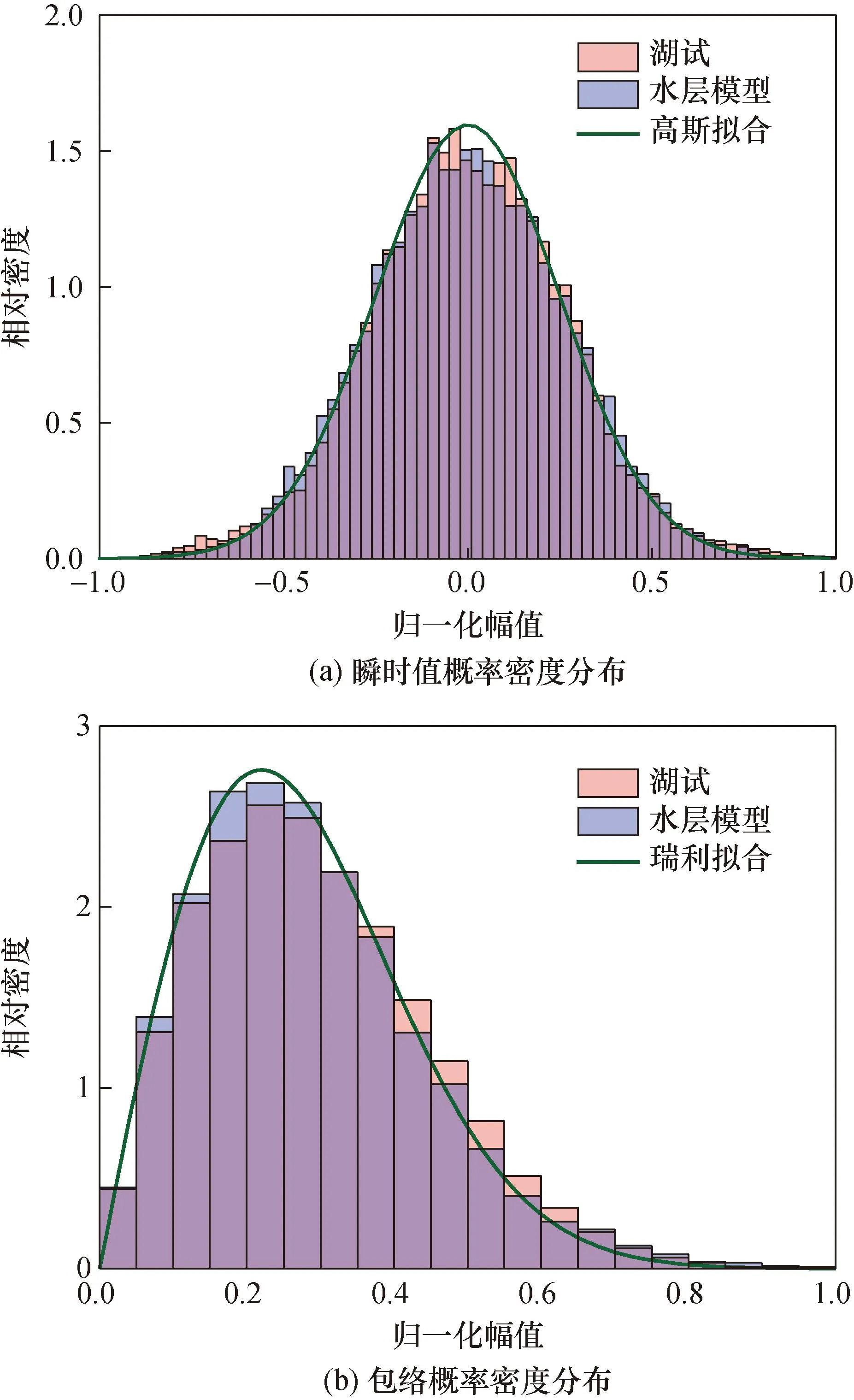
图9 水层仿真模型和湖试底回波统计特性

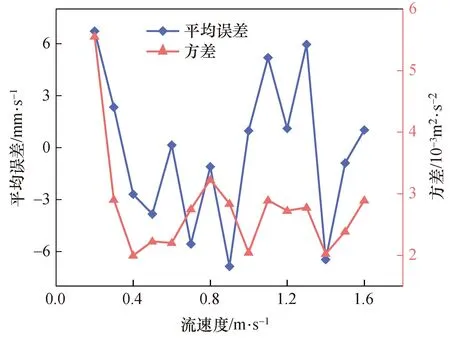
图10 水层回波速度误差及方差

6 多波束校准的波束间干扰

现阶段的水域环境ADCP校准中,大都是对ADCP的某一个波束进行校准。本文提出如图11所示的实验室水池环境下多个波束同时校准系统,其主体由ADCP和多个换能器组成,校准的原理为多个换能器同时回发所建立的回波模型信号,以此达到对ADCP底速度和流速度的校准。

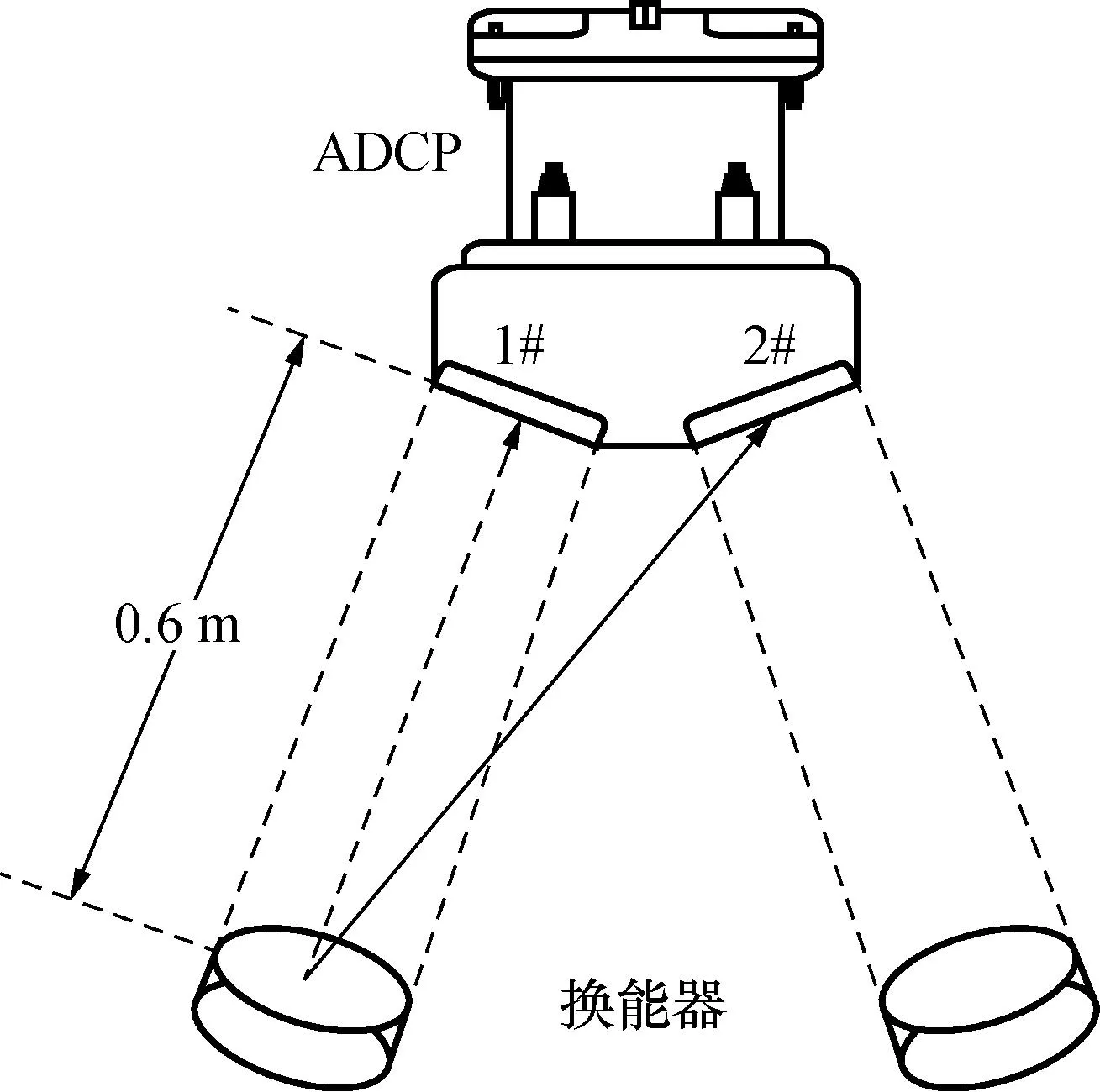
图11 ADCP多波束校准波束间干扰

在ADCP水池校准系统中,根据ADCP换能器的声轴声压分布情况[27],选择换能器距ADCP 0.6 m作为校准距离。在非开阔自由场环境中,ADCP的多个换能器同时接收回波,波束间的干扰不可忽略。在校准过程中,ADCP的2#换能器会接收到1#换能器的回波信号,并与其本身的回波信号产生混叠。由于ADCP所采取的是Janus结构,两个波束所携带的多普勒信息一个为正向频偏,另一个为负向频偏,两个信号混叠将会对速度的解析产生影响。

利用前述所建立的仿真回波模型,进行ADCP多个波束同时底回波校准中波束间干扰仿真探究。由于两个换能器轴线之间存在44°的夹角,所以其它波束作用在换能器的旁瓣区,通过仿真可得图12实验ADCP换能器波束图,此时旁瓣衰减为-30 dB。

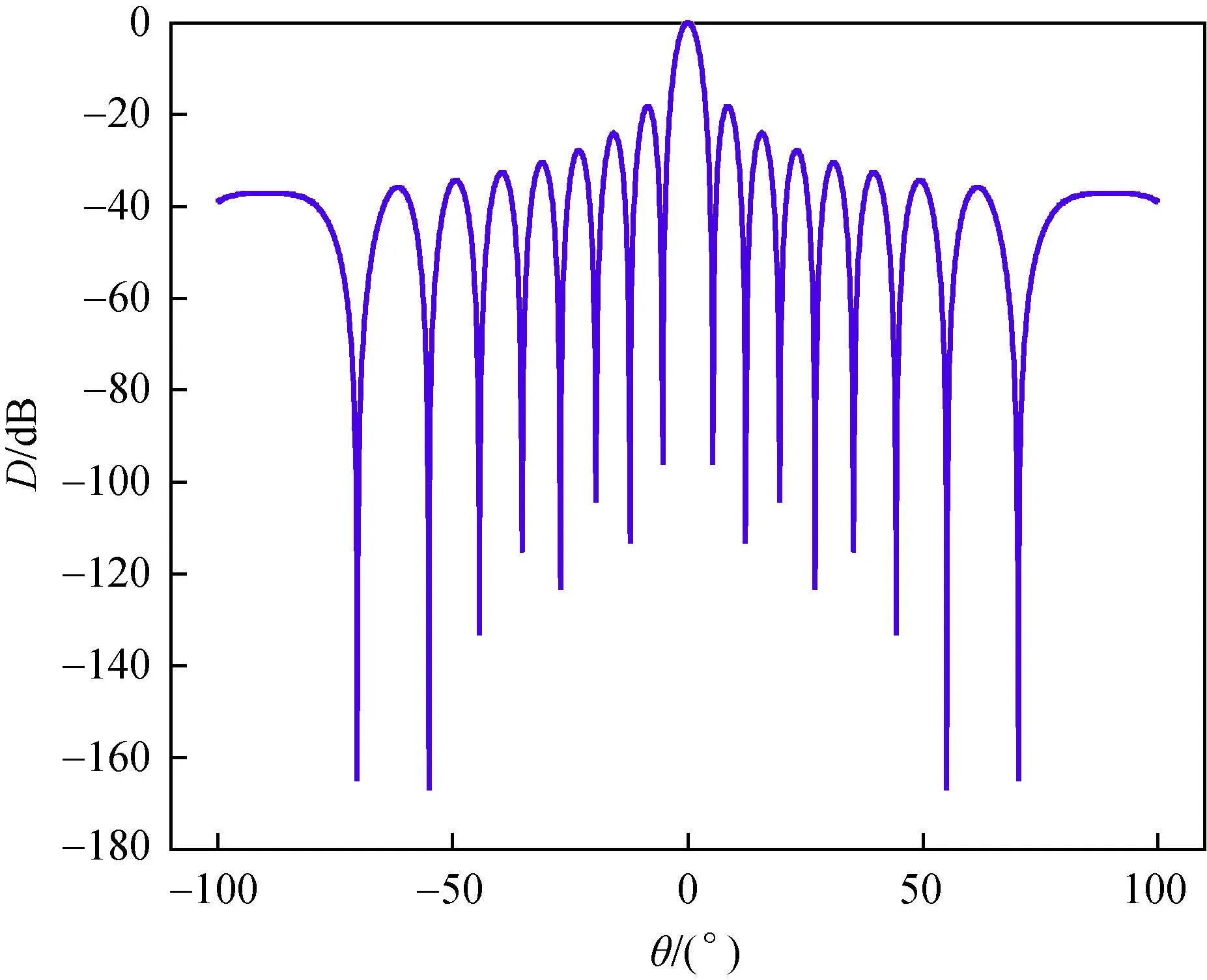
图12 实验ADCP指向性图

考虑其他波束底回波较主波束存在些许的延时。将其他波束的回波和主波束进行混叠,对比有无波束间干扰的校准底速度,解析速度误差如下。

图13所示为多个波束底回波校准中波束间干扰误差随速度变化结果。由图13可知,误差值与相对误差值随着速度增大而增大,其原因是两个波束的频偏值互为正负,且随速度增大而增大,则干扰也逐渐增大。观察相对误差的量级可知,其值在0.6%以下。实验ADCP的底跟踪测量精度为:±0.5%V±0.005 m/s(其中V为载体对地航速),由此可知在ADCP底跟踪多个波束校准中,速度为1.6 m/s及以下波束间的干扰影响都处于测量精度范围内,1.6 m/s以上的底速度校准中,波束间干扰将会带来校准误差,可以选用添加障板的方式进行抑制。

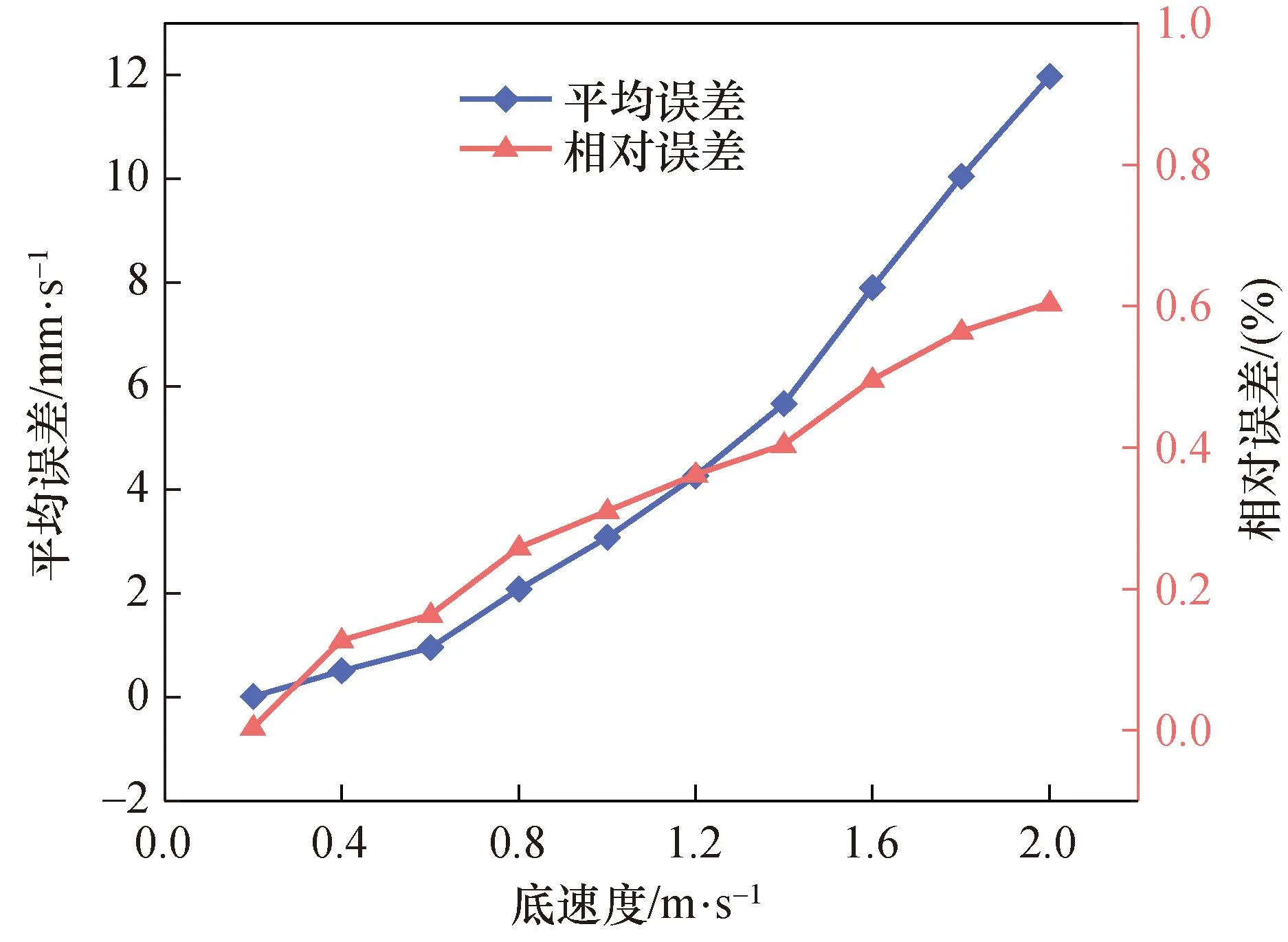
图13 底回波波束间干扰误差

同理对水层回波进行探究,在水层回波中设定了全水层统一流速和变流速两项测试,其中变流速采用递增和递减的双重线性变化,即随着水层增加流速值先增大,随后再减少。

图14所示为ADCP多个波束水层回波校准时的波束间干扰误差,可知误差与流速之间无明显关联,并且误差的数值普遍在毫米每秒以下。观察其相对误差可知,各速度值的相对误差都接近于0%。实验ADCP的流速测量精度为:±0.5%V±0.005 m/s(其中V为真实流速值),可知水层回波波束间的干扰对校准无影响。其原因为叠加的干扰是多个水层信号共同作用的结果,存在很大的随机性。

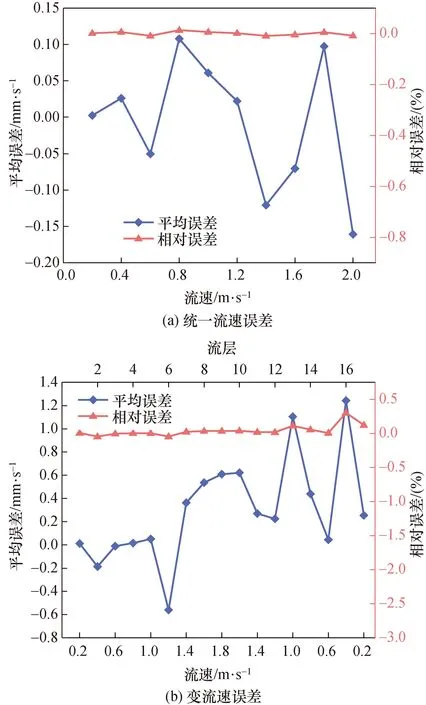
图14 水层回波波束间干扰

由于水层回波波束间的干扰误差表现出很强的随机性,故根据重复性实验的结果对其误差的分布规律进行分析。

如图15所示,水层回波的波束间干扰误差在分布上满足高斯分布,故可以认为ADCP多个波束流速度校准时,水层回波的波束间干扰是一个随机噪声,影响及其微弱,可以忽略。

图15 水层回波波束间干扰误差分布

同时针对不同型号的ADCP,其声束轴线角一般在15°～30°之间,造成的旁瓣衰减不同,故需对不同衰减值下的波束间干扰进行仿真探究。根据实验ADCP换能器的波束图,仿真选取的旁瓣衰减值在-20～-40 dB之间,能够覆盖绝大多数ADCP型号的换能器旁瓣衰减。

如图16所示,随着换能器的旁瓣衰减增大,波束间的干扰在减少并达到稳定。由图16可知在旁瓣衰减达到-25 dB时,干扰所带来的影响就达到了一个稳定的值,此时的相对误差非常小,不再随着衰减值的变化而变化。

图16 误差随旁瓣衰减值变化图

7 结 论

本文介绍了一种精确的ADCP回波仿真模型,依据此模型提出一种ADCP水池环境下多个波束同时校准的方法,并针对该校准方法存在的波束间干扰问题进行了仿真分析。这种校准方法通过对海底和水层中的散射物质进行仿真建模,构建了精准的底回波和水层回波模型,并进行实验对仿真模型在信号、统计规律和速度3个方面进行验证。实验验证了所建立模型的准确性,利用建立的模型信号回发给ADCP,即可实现对ADCP的多个波束同时精确校准。在多个波束同时校准中存在的波束间干扰,仿真结果表明底回波中干扰误差随着底速度增大而增大,当底速度超过阈值之后,误差将超过测量精度而造成干扰,需要对这个干扰误差进行有效规避;而水层回波的波束间干扰影响要小很多,其相对误差接近于0,分布规律也符合高斯分布,故其影响可以理解为一个高斯随机噪声。仿真结果还表明在对不同型号的ADCP校准时,波束间的干扰误差将逐渐趋于稳定。本文为ADCP的实验室水池校准提供了可行性方案,并且为后续的ADCP水池多个波束同时校准实验和系统开发奠定了基础。