一种突触可塑性导致的觉醒-睡眠周期中突触强度变化和神经动力学转变*

李瑞 徐邦林 周建芳2)† 姜恩华2) 汪秉宏 袁五届2)‡

1) (淮北师范大学物理与电子信息学院,淮北 235000)

2) (淮北师范大学,安徽省智能计算与应用重点实验室,淮北 235000)

3) (中国科学技术大学近代物理系,合肥 230026)

1 引言

行为学研究表明,长时间保持觉醒会对人的学习和记忆产生负面影响,睡眠则有助于学习和记忆的恢复[1-5].基于一些脑区的突触强度变化的实验结果[1,6,7],Tononi和Cirelli[5,7]提出了一种可能的“突触稳态假说”来解释这种现象.这种假说指出,学习导致了觉醒时突触强度的净增加,增加大脑能量消耗的同时降低了学习和记忆的效率;睡眠会将突触强度净减弱到维持能量的基本水平,使学习和记忆能力恢复.实验发现,这种突触强度变化通常伴随着神经动力学的转变[8-11].觉醒期间突触强度净增强伴随着神经电活动从强直性(tonic: 有节奏的单次峰值)发放到阵发性(burst: 多次峰值的重复序列)发放的转变,睡眠期间突触强度净减弱伴随着从阵发性发放到强直性发放的转变.另外,神经元群在觉醒状态下主要表现为不同步的强直性发放,在睡眠时则主要表现为具有阵发同步的阵发性发放,并进而产生慢波活动(slow-wave activity,SWA)[9,11,12].神经元群的这两种发放状态并不是觉醒和睡眠的显著区别.在觉醒状态的后期,也就是疲惫或困倦时,神经元群也可以表现为同步的阵发性发放[10,12,13];在睡眠状态的后期,也就是觉醒之前的浅睡阶段或是快速眼动睡眠期,一些脑电信号和功能核磁共振表明神经元群也可能表现为不同步的强直性发放[14,15].因此,神经元群在觉醒状态下是一个趋向同步化的过程,由初始不同步的强直性发放向同步的阵发性发放逐渐过渡;睡眠则是一个去同步的过程,在将突触强度降低到基准水平的同时,使具有阵发性同步的阵发性发放恢复到不同步的强直性发放.最新的理论研究表明,突触强度的变化可以导致上述神经动力学的强直性和阵发性发放的转变,这种动力学的转变源于突触电流的振荡特性[12,16].

上述实验和理论上的发现为行为学“突触稳态假说”提供了动力学机制上的基础,相应的理论研究需要建立具体的突触可塑性机制.然而,当前的这些理论研究仅使用简单的线性时变函数来模拟突触强度的变化[12,16],没有考虑产生这种变化的具体的突触可塑性机制.本文旨在建立一种突触可塑性模型,以实现觉醒-睡眠周期中自发调节突触强度的变化,进而引起相应神经动力学的转变.

在神经系统中,突触可塑性分为长时程可塑性和短时程可塑性,每种可塑性都有多种不同的类型[17-19].一些研究者认为,一种属于长时程可塑性的发放时序相关可塑性(spike-timing-dependent plasticity,STDP)负责大脑的学习和记忆功能[19-22],这种可塑性可以引起突触强度的长时程增强(long-term potentiation,LTP)和长时程减弱(long-term depression,LTD).一些改进的STDP模型也被提出,并用于模拟不同脑区或不同动物物种的实验观察结果[19,21,23,24].近年来,这些STDP模型受到了广泛的理论关注,特别是模型引起的神经网络自组织的突触权值(即突触强度)分布,例如双峰分布[21]、前向型网络分布[22,25]、幂律分布[20,26]等.目前,这些模型及其研究的理论结果在实验中得到了广泛的验证.相关实验表明,一些参与突触可塑性的神经递质和神经调质在觉醒和睡眠期间发生改变,包括乙酰胆碱、去甲肾上腺素、皮质醇等[2,27].因此,STDP在觉醒和睡眠状态下可能具有不同的特定属性.综合考虑“突触稳态假说”及其相关实验可以很自然地提出假设: 在觉醒状态下,突触可塑性的LTP起主导作用并进而导致突触强度净增强;在睡眠状态下,突触可塑性的LTD起主导作用并进而导致突触强度净减弱.本文基于一种突触权值依赖的改进STDP,提出一种觉醒和睡眠周期中的突触可塑性模型,在觉醒-睡眠周期中交替改变模型的参数,以实现觉醒-睡眠周期中突触强度的变化并进而引起相应神经动力学的转变.研究发现在长时间的觉醒或睡眠后,网络的平均突触权值将达到稳定值,并且稳定后的突触权值呈现出稳定的真实神经系统中观察到的对数正态分布.特别地,通过数值模拟和理论分析,本文深入地研究了这种改进的STDP的特定参数对稳定的平均突触权值及突触权值分布的影响.

2 模 型

2.1 神经元的网络耦合模型

考虑N个Hindmarsh-Rose (HR)神经元[28],这些神经元之间以概率p通过兴奋性化学突触随机相互连接,形成一个Erdős-Rényi (ER)随机网络[29].网络中,第i个神经元的动力学方程可以表示为

方程中,xi代表神经元膜电位,yi和zi分别表示与快电流和慢电流相关的量,Iext是外部输入电流.在方程(1)中,g是网络的全局耦合强度;反转电位Vs被设置为2,这意味着对于所有神经元i,在任意时刻t都满足Vs＞xi,即所有突触都是兴奋性化学突触[12].Aij(i≠j) 是网络连接矩阵的一个元素: 如果神经元j到神经元i之间有突触连接,则Aij=1,否则Aij=0;Wij(i≠j) 代表相应的突触权值(在Aij=1 时),其取值被限定在 [0,1] 之间.每个初始突触权值都随机且独立地在0—1的范围内选择,并且受到2.2节中改进的STDP影响;Gj是来源于神经元j的化学突触耦合函数,每当神经元j发放时,Gj增加一个常量 ΔG,其余时间,Gj以时间常数τ 指数衰减,即 dGj/dt=-Gj/τ[12,30,31].上述神经元动力学方程(包括Gj的变化方程)的参数选择如下:a=1,b=3,g=0.035,c=1,d=5,e=0.002,q=4,x0=-1.6,ΔG=1,τ=1.这些参数取值是很多经典文献中常用的,是依据实验并能够很好地模拟出实验结果的参数值[12,13].ER网络的参量取为N=100和p=0.2.需要指出的是,下面的结果并不依赖于N和p的具体取值,本文选择的N值不太大,是为了减少数值计算量.在动力学方程中,调节参数Iext可以使单个HR神经元表现出强直性或阵发性发放(详见文献[12]中的图1): 当Iext＞3.3 时,出现强直性发放;当1.27＜Iext＜3.3 时,出现阵发性发放.本文取Iext=3.6,在该值时单个(或无耦合)神经元表现出强直性发放.

2.2 突触权值依赖的STDP改进模型

原始的STDP模型中,突触强度的变化由突触前和突触后神经元发放的先后顺序及其相应的时间间隔值决定.当突触前神经元早于突触后神经元发放时,突触强度增强,反之则突触强度减弱[32].突触强度Wij的变化量 ΔWij由以下关系式给出:

其中,Δtij表示突触后和突触前神经元发放的时间间隔,即突触后神经元发放的时刻值减去突触前神经元发放的时刻值[21].(4)式中,Δtij≥0 表示突触前神经元发放早于突触后神经元发放,表示突触强度增强(LTP);Δtij＜0表示突触前神经元发放落后于突触后神经元发放,表示突触强度减弱(LTD).因为神经网络中的连接具有随机性,使突触前和突触后神经元的发放序列变得复杂.在进行数值模拟时,配对并计算所有突触前和突触后神经元的发放时间间隔比较困难.为了解决这个问题,本文引入变量Pi(t)和Mi(t) 来综合考虑所有突触前和突触后神经元之间的影响[21,20].Pi(t)和Mi(t) 分别是以时间常数τ+和τ-指数衰减的函数,满足dPi(t)/dt=-Pi(t)/τ+,dMi(t)/dt=-Mi(t)/τ-.每当神经元i发放时,Pi(t) 增加A+,Mi(t) 减少A-,所有与神经元i相连的突触权值Wij和Wji根据如下关系进行更新:

根据表达式(5),如果权值更新使得Wij＞1 (或Wji＜0),则Wij(或Wji)被取为最大权值1(或最小权值0).有研究发现,原始的STDP模型导致突触权值呈现双峰分布,即突触权值会集中在最大权值1和最小权值0的附近[21].还有一些不同的实验结果表明,在部分脑区突触权值呈现单峰分布.这种单峰分布常被认为是更稳定、更接近大脑真实情况的[33].因此,本文借鉴了一种突触权值依赖的改进STDP模型[33].避免了原始的STDP模型中突触权值总是被增强到最大值或减少到最小值附近的问题,并且可以模拟实验观察结果,即在强突触权值时的增强作用较弱.加入这种改进的STDP机制后,突触权值的更新关系式从原来的表达式(5)变为

式中,Pj(t)(cp+νWij) 表示突触强度的增加量,参量A+,τ+和cp反映突触强度增强的LTP特性;Mj(t)(cdWji+νWji)表示突触强度的减小量,参量A-,τ-和cd反映突触强度减弱的LTD特性.ν是均值为零、标准差为σν的高斯噪声.该更新关系式意味着,突触权值每次更新量不仅与突触前和突触后神经元发放的顺序和时间间隔有关,还受到当前突触强度和噪声的约束.

基于上述突触权值依赖的改进STDP,本文提出一种觉醒和睡眠周期中的突触可塑性模型,在觉醒-睡眠周期中交替改变模型的参数(包括A+,A-,τ+,τ-,cp和cd),使觉醒状态下,突触可塑性的LTP起主导作用;睡眠状态下,突触可塑性的LTD起主导作用.本文使用步长为 0.01 的四阶龙格-库塔法对神经网络的动力学方程组进行数值计算.每个神经元i的初始状态值在其动力学稳定后的数值范围内独立且随机选取,其中xi取值范围为 (-0.5,1.5),yi为 (-6,0.9),zi为 (3.1,4.2).

3 结果

3.1 突触强度的变化和神经动力学的转变

在STDP或改进的STDP的理论研究中,参数A+和A-常用于调节LTP和LTD的变化量[19].有实验结果表明,参与突触可塑性的一些神经递质和神经调质的数量和活性在觉醒和睡眠期间存在明显的变化,并且在觉醒时突触强度变化的幅度很可能大于睡眠时的变化幅度[34,35].因此在觉醒和睡眠周期中,突触可塑性模型中的参量值有很大可能也是有规律地变化,这种参量变化很难用明确的函数和数值进行描述,模型中的参量A+在觉醒时很可能大于A-,睡眠时则相反.在数值模拟中,为了减少参量的数量,简单地用A+和A-在觉醒-睡眠周期中以较短的时间相互交换数值来满足上述条件(见图1(a)).值得一提的是,以下的结果不仅限于A+和A-数值交换这种方法,只要满足上述A+和A-在觉醒和睡眠周期中的大小关系(即觉醒时A+＞A-,睡眠时A+＜A-)就可以得到相同的定性结果.由图1(b)和图1(c)可以看出,突触可塑性可以诱导觉醒-睡眠周期中的突触强度变化和神经动力学转变: 在觉醒期间,突触强度净增强,平均突触权值增加,导致神经电活动从强直性发放转变为阵发性发放;相反,在睡眠期间,突触强度净减弱,减小,导致神经元由阵发性发放恢复为强直性发放.

神经活动的转变经常伴随着网络同步性能的变化[12,16].为了探究上述过程中同步的演化,引入一种关于神经元发放同步的度量方法[36].首先构建如下的神经元发放序列: 在当前时刻向前取一个长度为T的时间窗口,并把它分成m个长度为ΔT的小时间段[37];神经元i的发放序列用Bi(n)表 示,n=1,2,···,m(m=T/ΔT),如果神经元i在第n个时间段内有发放,则令Bi(n)=1,否则Bi(n)=0;在时间演化过程中,让所取的时间窗口以时间步长 ΔT向后移动.然后用同步指数Syn(i,j)表示神经元i和j之间的发放同步度,Syn(i,j)定义如下:

整个网络的同步指数Syn定义为所有神经元对(i,j) 的同步指数Syn(i,j) 的平均值.本文选择参数T=400和ΔT=10.

接下来对觉醒-睡眠周期中的突触强度变化进行研究,并比较使用原始STDP ((5)式)和改进STDP ((6)式)的模型之间的差异.结果如图2(a)所示,在没有使用权值依赖的情况下,突触强度很容易达到Wmax=1 或Wmin=0 的饱和值.并且随着觉醒或睡眠时间的延长,观察到更多的突触权值集中到饱和值附近(见图2(b)).加入权值依赖后,突触强度的变化受到限制,即使在长时间的觉醒或睡眠后,突触权值也可能远离饱和值(见图2(c)和图2(d)).并且在长时间觉醒或睡眠后,权值依赖的改进STDP会使网络的平均突触权值和突触权值的分布都达到一个稳定的状态(见图2(d)).虽然每个突触的权值仍然随着神经元的发放进行更新,但是整个网络中突触权值的平均值几乎保持不变.我们将网络达到稳态时的平均突触权值定义为稳定的平均权值.下面详细研究含有权值依赖的STDP对稳定的平均权值(见3.2节)以及突触权值分布(见3.3节)的影响.

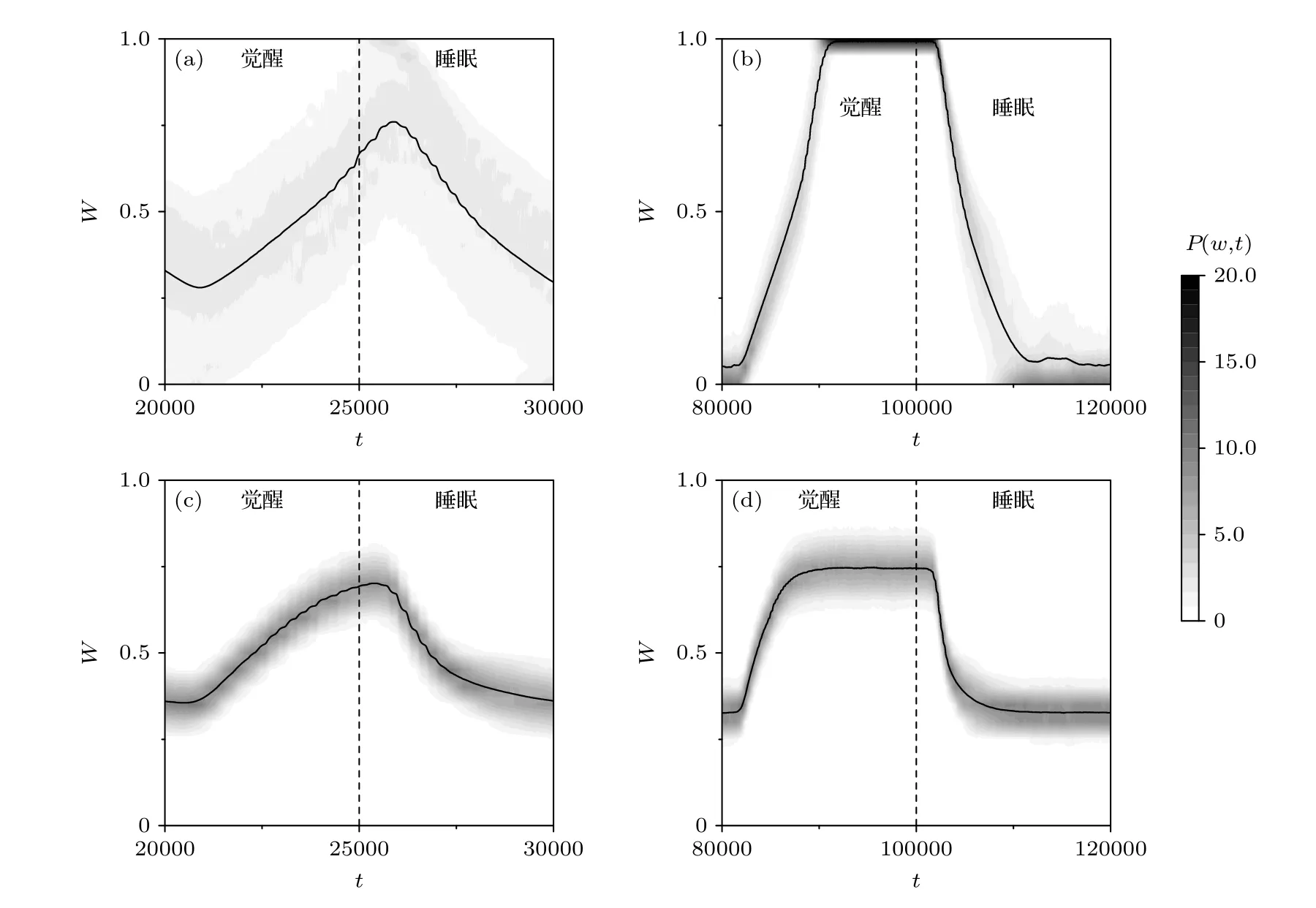
图2 在一个觉醒-睡眠周期内,突触权值分布概率密度 P (W,t) 的灰度图及网络平均突触权值的变化曲线(实线) (a),(b)不含有权值依赖的原始STDP情况;(c),(d)含有权值依赖的改进STDP情况;觉醒睡眠周期设置为10000 (a),(c) 和40000 (b),(d);垂直虚线表示觉醒和睡眠的交替时刻Fig.2.Gray-scale plots of probability density P(W,t) for weight distribution and the average synaptic weight (solid line) in the absence of weight dependence (a),(b) and in the presence of weight dependence (c),(d),for the different periods of wakefulnesssleep cycle,10000 (a),(c) and 40000 (b),(d).The vertical dashed lines indicate the moments of exchange between wakefulness and sleep.

3.2 稳定的平均突触权值

图3 稳定的平均突触权值 与比值 A+/A- 的函数关系 (a) cp=cd=1 固定不变,τ+/τ- 取不同的比值;(b) τ+=τ-=25 固定不变,cp/cd 取不同的比值.参数选择如下: A- 在 [0.002,0.01] 的范围内随机取值,A+ 的值通过A-乘以相应的比值得到;(a)中 τ-=25,τ+ 分别根据相应的比值计算给出;(b) 中 cp=1,cd 分别根据相应的比值计算给出.每个数据都是5次独立数值计算的平均数;为了对比,在图(a),(b)中分别用实线表示=0.5A+/A-,=A+/A- 和=2A+/A- 的线性关系Fig.3.Stable average weight as a function of A+/A- : (a) At different ratio τ+/τ- and cp=cd=1;(b) at different ratio cp/cd and τ+=τ-=25.Here,A- is given randomly in the range of 0.002 to 0.01,A+ is calculated and given by using the ratio of the corresponding parameter.τ-=25,and τ+ is calculated and given by using the ratios of the corresponding parameter in panel (a).cp=1,and cd is calculated and given by using the ratio of the corresponding parameter in panel (b).Data are averaged over 5 independent realizations.For comparison,the solid lines indicating the linear relations =0.5A+/A-,=A+/A-and =2A+/A- are shown in panels (a) and (b).

图4 稳定的平均突触权值 与比值 τ+/τ- 的函数关系 (a) cp=cd=1 固定不变,A+/A- 取不同的比值;(b) A+=A-=0.006 固定不变,cp/cd 取不同的比值.参数选择如下: τ- 在 [10,75] 的范围内随机取值,τ+的值通过 τ- 乘 以相应的比值得到;(a)中 A-=0.004,A+ 分别根据相应的比值计算给出;(b)中 cp=1,cd 分别根据相应的比值计算给出.每个数据都是5次独立数值计算的平均数;为了对比,在图(a),(b)中分别用实线表示=0.5τ+/τ-,=τ+/τ- 和=2τ+/τ- 的线性关系Fig.4.Stable average weight as a function of τ+/τ- : (a) At different ratio A+/A- with with cp=cd=1;(b) at different ratio cp/cd with A+=A-=0.006.τ- is given randomly in the range of 10 to 75,τ+ is calculated and given by using the ratio of the corresponding parameter.A-=0.004,and A+ is calculated and given by using the ratio of the corresponding parameter in panel (a).cp=1,and cd is calculated and given by using the ratio of the corresponding parameter in panel (b).Data are averaged over 5 independent realizations.For comparison,the solid lines indicating the linear relations =0.5τ+/τ-,=τ+/τ-and =2τ+/τ- are shown in panels (a) and (b).

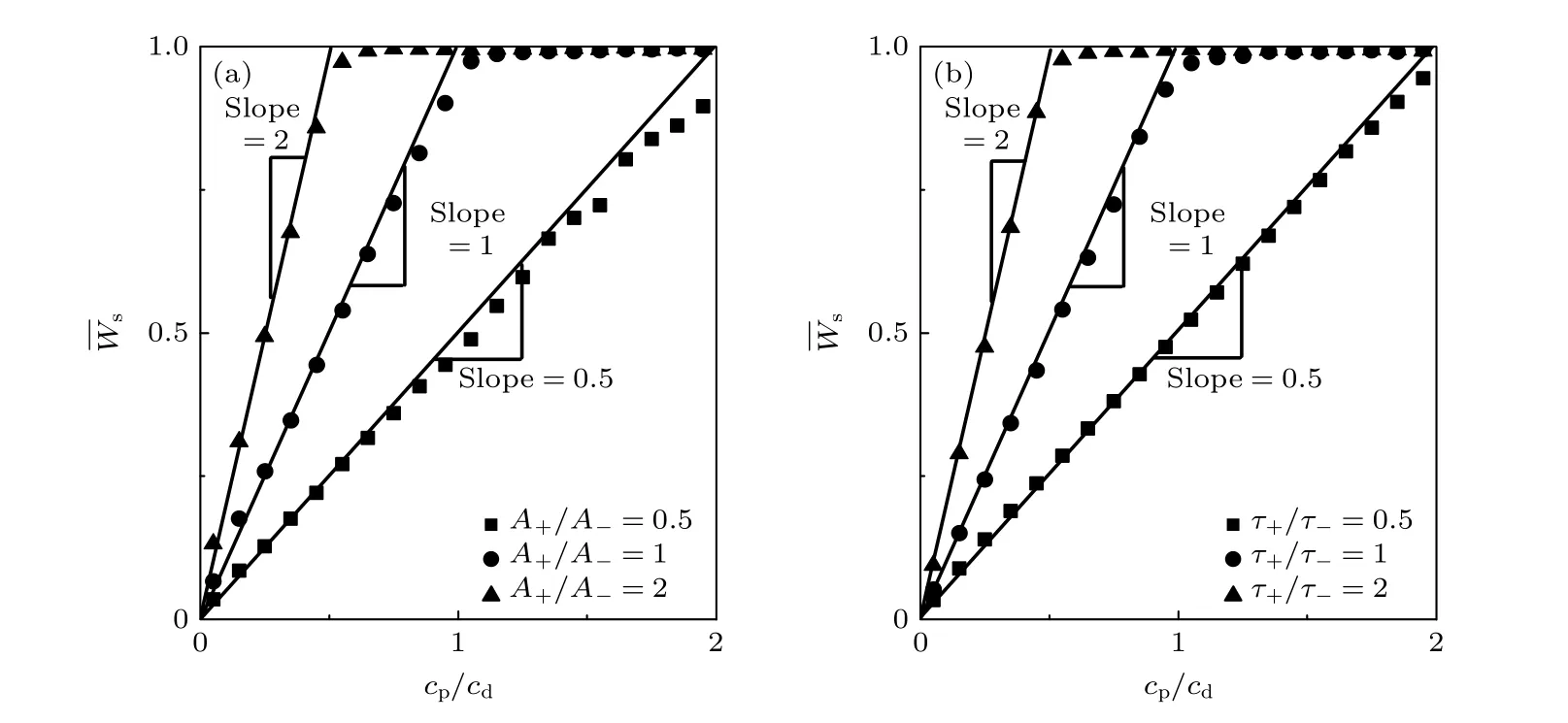
图5 稳定的平均突触权值 与比值 cp/cd 的函数关系 (a) τ+=τ-=25 固定不变,A+/A- 取不同的比值;(b) A+=A-=0.006 固定不变,τ+/τ- 取不同的比值.参数选择如下: cd 在 [0.5,2.5] 的范围内随机取值,cp 的值通过 cd 乘以相应的比值得到;(a)中A-=0.004,A+ 分别根据相应的比值计算给出;(b) 中 τ-=25,τ+ 分别根据相应的比值计算给出.每个数据都是5次独立数值计算的平均数;为了对比,在图(a),(b)中分别用 实线表示 =0.5cp/cd,=cp/cd 和=2cp/cd 的线性 关系Fig.5.Stable average weight as a function of cp/cd : (a) At different ratio A+/A- with τ+=τ-=25;(b) at different rations τ+/τ- with A+=A-=0.006.cd is given randomly in the range of 0.5 to 2.5,and cp is calculated and given by using the ratio of the corresponding parameter.A-=0.004,and A+ is calculated and given by using the ratio of the corresponding parameter in panel (a).τ-=25,and τ+ is calculated and given by using the ratio of the corresponding parameter in panel (b).Data are averaged over 5 independent realizations.For comparison,the solid lines indicating the linear relations =0.5cp/cd,=cp/cd and =2cp/cd are shown in panels (a) and (b).

下面对(8)式进行理论分析.

当网络的平均突触权值达到稳定时,意味着网络中突触强度的平均增加量与平均减小量相等.也就是说,表达式(6)中LTP和LTD部分在网络中的平均值相等,即:

如图1所示,当突触权值较小时,神经元表现出不同步的强直性发放.相反,当存在较大的突触权值时,神经元虽然表现出同步的阵发性发放,但是阵发性发放内的峰值仍然不同步.因此,网络在整个演化过程中任意的神经元i和j的发放时间间隔Δtij和Δtji都可以近似地被看作从-∞到 +∞的均匀分布.根据(4)式可以得到

(10)式是对稳定的平均突触权值进行理论分析的结果.当A+τ+cp/A-τ-cd＜Wmax=1 时,的理论值与数值模拟得到的结果((8)式)一致.而当A+τ+cp/A-τ-cd≥Wmax=1 时,的模拟结果总是接近1,小于理论值.这是因为突触强度Wij存在最大边界,而在理论分析中未考虑边界的影响.因此,本文的理论分析结果与数值模拟结果是一致的.

为了进一步验证(8)式(或(10)式)是否具有普遍性,令参数A+,A-,τ+,τ-,cp和cd分别在一定范围内随机取值,并进行大量的数值模拟,这些随机组合的比值A+τ+cp/A-τ-cd与相应的函数关系如图6所示.结果表明,数值模拟结果与(8)式(或(10)式)一致.

图6 稳定的平均突触权值 与比值A+τ+cp/A-τ-cd的函数关系.其中A+和A- 在 [0.002,0.01]范围内随机选取,τ+和τ- 在 [10,75] 范围内随机选取,cp和cd 在[0.5,2.5]范围内随机选取Fig.6.Stable average weight as a function of A+τ+cp/A-τ-cd.Here,A+ and A- are both chosen randomly in the range of 0.002 to 0.01,τ+ and τ- are both chosen randomly in the range of 10 to 75,and cp and cd are both chosen randomly in the range of 0.5 to 2.5.

3.3 稳定的突触权值分布

一些实验结果表明,大脑中某些脑区的突触权值表现为单峰分布[33].特别地,有些脑区还表现出对数正态分布[39,40].本文对平均突触权值达到稳定值后的突触权值分布情况进行了研究,结果如图7(a)所示.当平均突触权值达到稳定的时,突触权值的概率密度P(W) 呈现出单峰分布.并且对横坐标W取对数后,P(W) 服从一种类似的正态分布(见图7(b)),这种分布就是所谓的对数正态分布.在这种分布中,概率密度函数P(W) 存在一个最大值(即峰值)Pp,相应的突触权值Wp可称为最概然权值.从图7可以看出,这种对数正态分布受到突触可塑性模型中噪声ν的影响.很显然,随着噪声波动(即标准差σν)的增加,权值分布的范围变宽.下面详细地研究噪声波动对分布的影响.

图7 不同σν条件下突触权值分布的概率密度P(W)(a) 在线性-线性坐标中;(b) 在对数-线性坐标中.纵向虚线表示不同 σν的相应最概然权值Wp.参数选择如下:A+=A-=0.004,τ+=τ-=25,cp=1和cd=2.结果是20次数值计算的平均Fig.7.Probability density P(W) for different σν in linear-linear space (a),and in log-linear space (b).The vertical dashed lines indicate the corresponding most probable weights Wp for different σν.Here,parameters A+=A-=0.004,τ+=τ-=25,cp=1 and cd=2 are given.Results are averaged over 20 realizations.

如图8(a)和图8(b)所示,随着噪声波动(即标准差σν)的增加,权值分布的最概然权值Wp及相应的最大概率密度Pp都减小.σν的值较小时,稳定的平均权值与(10)式给出的理论值(见图8(a)中的水平虚线)非常一致.当σν增加到一临界值时,逐渐小于理论值,此时Pp刚好减小到一个饱和值.图8(c)显示了权值分布的标准差σW及其变分系数CV(标准差除以平均值)的变化.结果发现,σW和CV都随着σν的增加而增加,表明噪声波动的增加导致了突触权值波动的增加(即分布范围变宽).但是,当σν增加到上述的临界值时,σW将增加到一个饱和值.很显然,σν存在一个相同的临界值(见图8中σν=6 处的垂直虚线),当σν超过该临界值时,小于理论值,Pp或σW也都减小或增加到一个饱和值.这是由于当σν达到该临界值时,部分突触权值增加到Wmax而被设置为最大值1导致的(见图7中σν=6 时的曲线).也就是说,这种现象是由权值的最大边界引起的.

图8 稳定的突触权值分布的各特征量与 σν 的函数关系(a) 平均突触权值和最概然权值 Wp;(b) 概率密度峰值 Pp;(c) 突触权值的标准差σW和变差系数 CV.为了比较,图(a) 中水平虚线表示用(10)式计算的 的理论值;垂直虚线表示 σν 的临界值.参数选择如下:A+=A-=0.004,τ+=τ-=25,cp=1和cd=2.结果是20次 数值计算的平均Fig.8.Characteristic quantities of the stable synaptic weight distribution as a function of σν : (a) The average synaptic weight and the most probable weight Wp;(b) the most probability density Pp;(c) the standard deviation of weight σW and the coefficient of variation CV.For comparison,the theoretical value of in Eq.(10) is shown by using the horizontal dashed line in panel (a).The vertical dashed line denotes the critical σν.Here,parameters A+=A-=0.004,τ+=τ-=25,cp=1 and cd=2 are given.Results are averaged over 20 realizations.

4 结论

综上所述,基于权值依赖的改进STDP,本文提出了一种觉醒和睡眠周期中的突触可塑性模型,通过调节觉醒和睡眠周期中该模型参数A+,A-,τ+,τ-,cp和cd的数值,只要使觉醒时A+τ+cp/A-τ-cd的值比睡眠时大,就可以实现: 觉醒时突触强度净增强及其导致的神经动力学从强直性发放到阵发性发放的转变,睡眠时突触强度净减弱及其导致的神经动力学从阵发性发放到强直性发放的转变.无论是在长时间的觉醒还是睡眠后,本文提出的突触可塑性所产生的平均突触权值都能达到一个稳定的.通过数值模拟和理论分析发现,当没有达到最大的饱和值Wmax=1 时,=A+τ+cp/A-τ-cd,即该值取决于模型中代表LTP和LTD的各参数乘积的比值.特别地,当平均突触权值达到稳定的时,突触权值的分布呈现出稳定的真实神经系统中观察到的对数正态分布.并且,这种分布受到突触可塑性模型中噪声波动的影响: 随着噪声波动的增加,权值分布的范围变宽,分布的最概然权值以及相应的最大概率密度均减小.值得一提的是,本文在ER网络上得到的上述结果不依赖于网络的类型,例如,在无标度网络或小世界网络上也有相同的结果.本文的研究结果可为觉醒-睡眠周期中突触可塑性及其神经元发放的生理机制研究提供理论参考,并在睡眠障碍治疗或干预措施的开发中具有潜在的应用价值.