基于平行平板电极的非球面双液体透镜的仿真与实验分析*

孔梅梅 董媛 徐春生 刘悦 薛银燕 潘世成 赵瑞

1) (南京邮电大学电子与光学工程学院、柔性电子(未来技术)学院,南京 210023)

2) (南京南瑞信息通信科技有限公司,南京 211100)

1 引言

可变焦液体透镜由于其结构简单、操作方便、尺寸小等优点在成像[1]、光电信息集成[2]和生物医学[3]等方面得到广泛应用.目前已提出的能够实现可变焦液体透镜装置中,所采用的主要原理有电化学[4]、热效应[5]、流体压力[6]、电润湿[7,8]和介电泳[9,10].其中,基于电润湿和介电泳的电控液体透镜的研究最多,然而由于接触角的饱和,液体透镜中大多数仅允许在保持球形形状的同时调节焦距[11].为了获得高像质的成像结果,研究者尝试采用固液相结合的透镜结构形式,比如,2017年Zhang等[12]提出了一种可以用来消除像差混合式可变焦液体透镜.但是,这种固液混合式的透镜结构的像差校正仍主要依赖于固体球面透镜,不仅整个透镜结构的复杂性增大而且像质优劣仍受限于固体球面透镜,因此,为了简化结构,并提高成像质量,人们直接在液体透镜中引入了非球面,并展开了一系列相关的研究.

目前国内外有关非球面液体透镜的研究,主要有2008年Hung等[13]提出了以静电梯度力调制非球面微透镜,但是需要高驱动电压,实用性受限.2010年新加坡国立大学Yu等[14]通过在制造过程中将高精度单点金刚石车削(SPDT)引入到标准的软光刻工艺中,以获得非球面.利用该设计,可以补偿与常规设计相关联的球差.结果表明,在特定的工作区域内,透镜相关的光学性能可以得到显著改善.然而,该装置制备工艺复杂,不利于透镜的快速和低成本生产.荷兰Twente大学的Mishra和Mugele[15],Lima等[16]以及Mishra等[17]分别于2016—2019年提出了利用流体静压力和电场力共同调节双液体界面面型的曲率和椭球度,得到相应的非球面面型.通过使用100个可单独寻址电极阵列,Lima等[16]演示了不同类型的光学像差的调节,例如像散、彗差和球差.然而图案化的电极无疑增加了器件制造的复杂性.Chen等[18]于2020年通过使用两个阵列的电极条对称地控制两个空气/液体界面的介电泳效应.每个电极的独立控制使得容易将空气/液体界面调整为任意非球面形状,从而能够消除面内光流体透镜的球差.本课题组分别于2016年[19]和2019年[20],基于液体的密度差,在双液体透镜和三层液体透镜中分别引入了非球面面型,分别进行了相关的光学特性分析和非球面三层液体透镜在人眼晶状体光学模型中的应用研究.

在我们之前的研究基础之上,本文通过仿真与实验分析,研究了一种基于平行平板电极的非球面双液体透镜结构.通过理论仿真,结合球面液体透镜,对比分析了不同电压下的非球面界面面型的焦距变化,并对其焦距和成像质量进行了实验分析,实验结果与仿真基本一致.与图案化电极相比,该非球面液体透镜结构使用连续电极,加工更简单,成本更低,更易于实现,更具有实用性.

2 基本理论与结构设计

介电泳(dielectrophoresis,DEP)是一种将粒子置于非均匀电场中时发生的现象.当带净电荷的粒子被置于电场中,电场会使粒子产生极化,携带的电荷不均匀分布在介质界面,其沿着电场线受力,如果电场是非均匀的,那么电场强度较高的区域的极子会占据主导地位,粒子产生移动,产生介电泳现象.

当不施加电压时,液滴处于放松状态,此时液滴的曲率最小.当施加电压时,两种液体受到电场力作用.对于液滴,其内部的电场可以表示为

参数设置如图1所示.ε1,ε2和εp分别代表环境液体、液滴和介质层的介电常数;h是腔体高度,dp是介质层的厚度,U是外加电压,t是液滴沿着垂直方向从液滴曲面到介质层表面的高度.

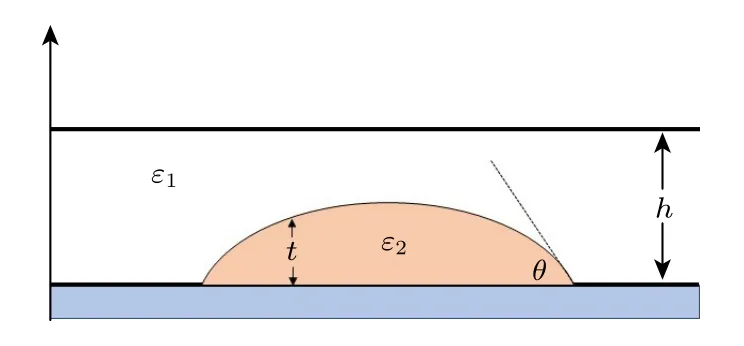
图1 液体透镜参数设置示意图Fig.1.Schematic diagram of parameter setting of the liquid lens.

在(1)式中,假设介质层涂覆得非常薄,即dp→0,那么dp/εp对电场Et的影响可以忽略.在这种情况下,液滴边缘附近的电场可以近似为

假设液滴的顶点非常地接近腔体的高度,即t→h.那么液滴顶点处的电场Et可以近似为

从(2)式和(3)式可以看出,液滴边缘附近的电场强度是顶点处的ε1/ε2倍.由于液滴的表面是连续变化的,因此电场呈梯度分布,液滴受到非均匀电场力的作用,产生介电泳现象,液滴受到的介电泳力[21]为

其中ε0表示真空中的介电常数,ε1表示环境液体的介电常数,ε2表示液滴材料的介电常数.由(4)式可以看出,介电泳力与液体材料的介电常数差成正比.

基于介电泳原理,所设计的非球面双液体透镜结构示意图如图2所示,该双液体透镜主要由上下两块ITO导电平面玻璃板、腔体、介质层和疏水层组成.其中,ITO导电玻璃上涂覆的介质层和疏水层分别采用SU8和Parylene溶液.腔内的环境液体和液滴材料分别采用去离子水(密度为1000 kg/m3,介电常数为78.36,折射率为1.333)和甲基硅油(密度为970 kg/m3,介电常数为2.7,折射率为1.403),二者存在较大的介电常数差,由(4)式可知,可产生较大的介电泳力.由于无需使用标准光刻工艺对电极进行图案化处理,所以,与平面环形电极和径向叉指电极等各种不同的图案电极形式相比,该结构更简单,更易于制造和批量化生产.

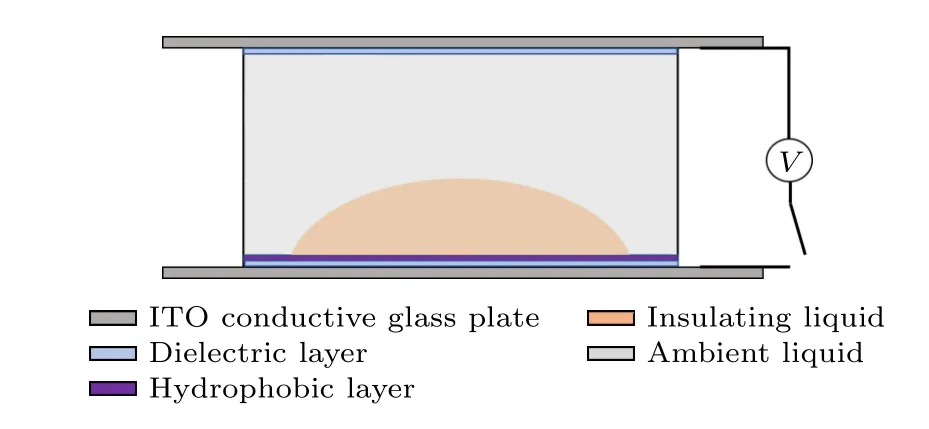
图2 基于平行平板电极的非球面双液体透镜的结构原理示意图Fig.2.Structural principle diagram of the aspherical double-liquid lens based on parallel plate electrode.

3 仿真分析

非球面双液体透镜建模的仿真流程图如图3所示,主要包含3个部分的内容.首先利用Comsol软件建立不同电压下的双液体透镜的模型,导出界面面型数据,然后利用Matlab软件拟合界面得到相应的非球面系数,最后利用Zemax软件建立相应的非球面双液体透镜光学模型.

图3 利用软件进行非球面双液体透镜建模的仿真流程图Fig.3.Simulation flow chart of aspherical double-liquid lens modeling with softwares.

利用Comsol软件,首先构建高5 mm的腔体,封装腔体的上下为ITO导电平面玻璃板(厚度均为0.7 mm).其次,在材料中添加液滴和环境液体,其中甲基硅油液滴在底面覆盖半径约2.7 mm,环境液体设置为去离子水,随后在上下平面玻璃板添加电场,得到的模型如图4所示,其中图4(a)是它的立体斜视图,图4(b)是当施加电压40 V时,基于上下ITO导电玻璃的平行平板电极所产生的电场线分布示意图.对整个非球面双液体透镜模型进行网格划分,并对双液体界面处进一步细化.最后,对模型施加不同的电压,得到不同电压下非球面面型数据.

图4 Comsol中的非球面双液体透镜模型 (a) 立体斜视图;(b) 电场线分布图(40 V)Fig.4.A spherical double-liquid lens model in Comsol:(a) Stereoscopic oblique view;(b) electric field line distribution diagram (40 V).

基于Comsol中得到的非球面面型数据,利用Matlab软件,采用(5)式所示的非球面公式进行拟合,可以获得不同电压下的面型图和其相应的系数[22]:

其中a表示双液体界面的位置;b,c,d,e,f表示多项式系数.表1展示了不同电压下非球面面型的拟合精度,通常R-Square的值越接近于1,拟合精度越好,从表1可以看出,该值均大于0.99,拟合精度非常高.图5是施加电压280 V时双液体透镜的非球面面型拟合图.

表1 不同工作电压下面型拟合精度(R-Square值)Table 1.Precision of surface fitting under different working voltages (R-Square value).

图5 利用Matlab拟合的280 V电压下的界面面型图Fig.5.Surface diagrams of interfaces fitted with Matlab under the voltage of 280 V.

传统的双液体透镜的界面面型是以球面变化的,为了进一步研究非球面双液体透镜的特性,遂将其与球面的特性进行对比.球面液体透镜的界面曲率半径R和外加电压U的关系以及焦距f′和外加电压U的关系[23]为

其中θ0为零电压下的接触角,V为液滴的体积,γm为液滴和环境液体之间的界面张力,d为介电层的厚度,nr为液滴的折射率,nm为环境液体的折射率.通过(6)式可以计算出不同电压下球面双液体透镜的曲率半径,从而就可以在Zemax中建立相关的光学模型.基于Matlab拟合得到的不同电压下的多项式系数,利用Zemax软件,建立相应的非球面双液体透镜的光学模型;球面双液体透镜的液体材料、腔体结构和液滴体积设置与非球面双液体透镜保持一致.将上述两种模型进行对比.

图6展示了工作电压为320 V时非球面与球面双液体透镜的光路图,像面选取为高斯面,可知非球面双液体透镜的球差明显小于球面,前者在像面上形成的圆形弥散斑也明显小于后者.

图6 同一电压(320 V)非球面和球面双液体透镜的光路图 (a) 非球面双液体透镜;(b) 球面双液体透镜Fig.6.Optical path diagrams of aspherical and spherical double-liquid lenses surface at 320 V: (a) Aspherical doubleliquid lens;(b) spherical double-liquid lens.

当工作电压由0 V逐渐增加至340 V,通过Zemax软件中建立的不同电压下的模型仿真得到非球面双液体透镜的变焦范围,通过(7)式计算得到相同电压变化下的球面双液体透镜的变焦范围,将两者的变焦范围和成像质量进行了比较分析.

图7展示了不同电压下非球面与球面双液体透镜的焦距对比图,可以看出,前期当施加电压为0—180 V时,两种液体透镜的焦距变化基本一致.随着施加工作电压的逐渐增大,两者的差距逐渐变大.当工作电压在0—340 V之间调节时,非球面双液体透镜的变焦范围为52.7171—23.1045 mm,变焦比约为2.28;球面双液体透镜的变焦范围为52.2746—34.9423 mm,变焦比约为1.5.由此可以看出,在调节焦距方面,非球面双液体透镜的调焦范围要比球面双液体透镜大.

图7 不同电压下非球面与球面双液体透镜的焦距对比图Fig.7.Comparison of focal lengths between aspherical and spherical double-liquid lenses at different voltages.

光学系统的成像点列图的RMS半径(root mean square radius)即均方根半径,它是一个重要的半径参数,可以反映由像差引起的弥散斑的大小,是可直观地表征光学成像质量的一个重要参数指标.图8展示了不同电压下非球面与球面双液体透镜的成像点列图的RMS半径对比情况,可以看出,当工作电压在0—160 V之间时,两种透镜的RMS半径几乎没有差距;当工作电压在160—280 V时,球面双液体透镜的RMS半径从1.71 mm增大到3.38 mm,而非球面双液体透镜的RMS半径从1.67 mm增大到2.35 mm,增加幅度明显小于球面双液体透镜.随着工作电压继续增大,球面双液体透镜的RMS半径迅速增大,当工作电压为340 V时,RMS半径6.5 mm;而非球面双液体透镜的RMS半径逐渐减小到1.9 mm.图8也给出了当工作电压为320 V时非球面和球面双液体透镜的具体点列图示例,相同标尺下,可以明显地看出非球面双液体透镜的成像光斑比球面的小得多.图8的结果表明,随着工作电压的增加,球面双液体透镜的弥散斑大小不断增加,成像质量逐渐变劣,相反非球面双液体透镜的弥散斑大小先缓慢增加后逐渐减小,且增值范围仅有1.07 mm,远小于球面透镜,综上非球面双液体透镜的成像质量优于球面透镜.

由于刚施加电压(0—160 V)时,非球面液体透镜中液体界面的变形不明显,与球面面型相似,所以,成像的弥散斑大小也与球面的液体透镜相似,先缓慢增加;而随着工作电压的逐渐增大,液体界面的形变变大,非球面面型的非球面性逐渐显现,对像差的校正能力逐渐提高,所以弥散斑先增大后又逐渐减小.

4 实验分析

4.1 实验制备

实验中所用ITO导电玻璃的尺寸为19 mm×24 mm,厚度为0.7 mm,首先用无水乙醇对ITO玻璃片正反两面进行完整洗涤,接着用无尘纸进行擦拭,去除表面可见乙醇;放入超声波清洗仪中,利用去离子水清洗电极3 min左右,清洗完毕之后关闭清洗仪,取出玻璃片再次用无尘纸擦拭干净.在ITO板上先后涂覆SU8和Parylene溶液,选择圆柱形透明亚克力管作为腔体材料,尺寸为外径17 mm,内径13 mm,壁厚2 mm,高5 mm.使用紫外固化剂以及紫外固化灯照射,在处理好的ITO导电玻璃片上固定腔体.然后先注入约6/7腔体体积的去离子水,后将甲基硅油滴在疏水层的中心,注入的甲基硅油液滴在松弛状态时覆盖半径约为2.7 mm,再注入去离子水至液面高于腔体呈微凸起状态,最后使用UV胶将上层ITO导电玻璃片与腔体连接,完成封装,成品如图9所示.

图9 制备的基于平行平板电极的非球面双液体透镜实物图Fig.9.Actual image of prepared aspheric double-liquid lens based on parallel plate electrode.

4.2 焦距测量

使用实验室自制的焦距仪,通过记录目镜中不同线对的位置读数,来测试并计算出所制作的液体透镜的聚焦能力.测量原理如图10所示[24].

图10 放大率法焦距测量原理 (a) 焦距测量原理;(b) 玻罗分划线Fig.10.Magnification method focal length measurement principle: (a) Principle of focal length measurement;(b) the Porro dividing line.

平行光管物镜焦平面上从内向外依次有三组玻罗分划线,三组线对关于光轴对称,其间距为y,平行光管物镜的焦距为;分划板经过被测透镜在其像方焦面上成像y′,经读数显微镜物镜成像面上y′′,M0为读数物镜的放大率.读数模块由物镜和测微目镜组成.转动测微目镜使目镜焦面上的分划板上瞄准用的叉丝线与分划线相平行,固定目镜;接着调节读数旋钮使叉丝作横向移动,直至叉丝对准最右边的分划线无误差,随即可开始进行读数测量,原理是依据放大率法来测量焦距.

从几何光学原理可知y′′与y′的关系为

被测透镜的焦距可以表示为

根据(9)式和(10)式可整理为

将所制备的非球面双液体透镜置于焦距仪的可伸缩测量台,记录不同电压下三组线对的读数,结合(11)式计算出不同电压下的非球面双液体透镜的焦距值.如图11所示,当工作电压在0—280 V时,仿真的非球面双液体透镜的焦距值为52.7171—34.1314 mm;实验测得的焦距值为54.2391—34.5855 mm,实验与仿真的焦距变化基本一致.

图11 不同电压下仿真与实验测得的焦距对比图Fig.11.Comparison of focal length measured by simulation and experiment at different voltages.

4.3 成像分析

利用该非球面双液体透镜对USAF 1951分辨率板进行成像实验分析,得到不同电压下的成像结果如图12所示.从图12可以看出,当工作电压为0 V时,液滴处于放松状态(图12(a)),非球面双液体透镜的分辨率为14.254 lp/mm (第3组的第6号元素);随着电压增加,液体界面逐渐凸起,成像范围逐渐缩小,焦距逐渐减小,成像质量逐渐提高,如图12(b)所示非球面双液体透镜的分辨率最大可达到45.255 lp/mm (第5组的第4号元素),此时的工作电压为280 V.

图12 不同状态下非球面双液体透镜的分辨率图 (a) 0 V;(b) 280 VFig.12.Resolution of aspherical double-liquid lens in different states: (a) 0 V;(b) 280 V.

5 结果与讨论

本文利用介电泳原理,研究了一种基于平行平板电极的非球面双液体透镜,通过理论仿真建立了相关的光学模型,得到不同电压下非球面双液体透镜的焦距和成像点列图的RMS半径,并与球面双液体透镜模型进行了变焦范围和成像质量的比较分析.结果表明,非球面双液体透镜的变焦范围大于球面双液体透镜,前者的像质也优于后者.对所设计的非球面双液体透镜器件进行了实验制备,测量了其焦距和成像分辨率,当工作电压为0—280 V时,焦距的变化在54.2391—34.5855 mm范围内,与仿真基本一致,实验验证了该液体透镜结构的可行性,而且其成像分辨率最大可达到45.255 lp/mm.

本文所设计的非球面双液体透镜,虽然与2008年Ren等[25]提出的基于连续平板电极的可变焦液体透镜结构相似,但是他们的结构尺寸和调焦范围都是微米数量级,也未具体讨论液滴界面的非球面特性,而本文中的都是毫米数量级;而且,本文的液体透镜与2022年Xu等[26]提出的一种基于新型透明电响应液体己二酸二丁酯DBA (微毒)的球面液体透镜相比,都是结构简单的平凸透镜,结构尺寸都在毫米数量级,其分辨率约为28.5 lp/mm,而本文所提出的非球面液体透镜的分辨率最大可达到45.255 lp/mm,像质优于他们所提出的液体透镜.并且,本文的非球面液体透镜具有结构简单、易于实现的特点,与图案化电极相比,加工更简单,更具有实用性.