基于偏差补偿TCN-LSTM 和梯级迁移策略的短期风电功率预测
宋技峰,彭小圣,杨子民,段睿钦,周彬彬,陈凯,王有香
(1. 强电磁工程与新技术国家重点实验室(华中科技大学),电力安全与高效湖北省重点实验室(华中科技大学),武汉 430074;2. 云南电力调度控制中心,昆明 650011)
0 引言
随着“双碳”目标下新型电力系统建设的不断推进,风电装机规模持续上涨,不断有新建风电场并网发电。对于这些新建风电场,由于其未积累充足的历史运行数据,因而难以按照常规深度学习方法[1-4]直接训练完备的功率预测模型[5]。为解决这一问题,可以借助先进的迁移学习手段[6-8],为新建风电场引入相关风电场的历史数据或完备的预训练模型。
对于风电功率预测[9-11],迁移学习的可迁移对象包括数据和模型。数据迁移本质上是一种数据扩充手段,主要是采用相关性分析等方法从源风电场筛选出大量符合目标风电场规律的相似历史样本,再将这些样本视为目标风电场的历史样本,进而获取充足的历史运行数据来训练功率预测模型。模型迁移则是采用参数赋值和微调复训练等方法将源风电场训练好的完备功率预测模型迁移至目标风电场。
在深度学习预测建模上,时间卷积网络-长短时记忆网络(temporal convolutional network-long short term memory neural network, TCN-LSTM)是一种前沿的神经网络,其进一步强化了对时序特征的解析能力[12-15],近年来被逐渐应用于时间序列预测问题[16-18]。本文选用TCN-LSTM 网络作为预测建模的基本模型。
在风电功率预测方法上,采用偏差补偿方法对风电功率的预测偏差进行补偿修正,能有效提升预测精度。偏差补偿方法包含两个由不同数据集训练的独立网络,分别对功率和偏差进行预测,再将二者的预测结果叠加,进而得到最终的功率预测结果。文献[19]采用经粒子群算法优化的极端梯度提升法(extreme gradient boosting, Xgboost)作为功率预测模型,采用传统随机森林作为偏差补偿模型。文献[20]采用优化后的循环卷积网络作为功率预测模型,采用Xgboost 作为偏差补偿模型。文献[21]则采用极限学习机和多层感知机分别作为功率预测模型和偏差补偿模型。不难发现,上述研究多侧重于优化功率预测模型,偏差补偿模型则较为浅层,然而偏差序列中蕴含的信息与功率序列应当是同量级的。此外,在将该方法用于新建风电场时,由于新建风电场的历史样本不足,因而难以将样本等分为两份分别独立微调两个预测模型。
近年来数据迁移方面的前沿研究表明,将源域的数据按照相似度排序分批迁移,不同批次分别训练不同的网络结构,取得的效果优于一次性迁移所有数据训练整个网络。在此基础上,文献[5]进一步提出了一种基于多层次数据迁移的风电功率预测方法,采用相关性逐步增强的源域数据由浅入深地训练神经网络的各个隐层,并通过算例证实了这种分级迁移方式的有效性。然而在模型迁移方面,现阶段的模型微调策略通常是采用目标域的数据一次性地微调整个神经网络。这种方式在模型结构简单时能满足需求。但随着风电功率预测模型深度的不断增加,这种微调方式难以保证根据目标域的特征有效地优化整个神经网络。因此将数据迁移中由浅入深的网络训练思想用于模型迁移,对模型进行梯级微调,有望进一步提升迁移模型的预测精度。
本文提出基于偏差补偿TCN-LSTM 和梯级迁移策略的短期风电功率预测方法,采用结构相同的两个TCN-LSTM 网络分别作为源风电场的功率预测模型和偏差补偿模型,并采用模型并联融合的方式构造计及偏差的组合功率预测模型,提升了偏差补偿方法在模型迁移上应用的可行性,再采用梯级迁移策略逐级微调模型结构,最后通过算例验证了所提方法的优势。
1 基于偏差补偿TCN-LSTM 和梯级迁移策略的短期风电功率预测
1.1 总体框架
本文提出基于偏差补偿TCN-LSTM 和梯级迁移策略的短期风电功率预测方法,整体框架如图1所示。该模型分为两个阶段,分别为:1)为源风电场训练基于偏差补偿TCN-LSTM 的风电功率预测模型;2)采用目标风电场的数据对源风电场的模型进行梯级微调。
这两个阶段包含7个步骤。
1)步骤1,训练基于TCN-LSTM 的功率预测预训练模型。将源风电场的历史样本划分为两份,分别记为训练集A 和数据集B。采用训练集A 为源风电场训练基于TCN-LSTM的功率预测模型。
2)步骤2,为源风电场训练基于TCN-LSTM的偏差补偿模型。依据偏差补偿方法,基于与步骤1 相同结构的TCN-LSTM 网络,采用数据集B 为源风电场训练偏差补偿模型。
3)步骤3,功率预测模型与偏差补偿模型并联融合。将步骤1 获取的功率预测模型和步骤2 获取的偏差补偿模型并联融合,构成计及偏差的组合功率预测模型。
4)步骤4,将目标风电场的数据按照与源的相关性分为两份。基于目标风电场历史样本和源风电场历史样本的相关性排序,将目标风电场的历史样本集分为二等分,分别构成强相关数据集和弱相关数据集。
5)步骤5,采用强相关数据集对TCN 模块进行微调。本文采用的TCN-LSTM 模型包含两个TCN 模块和两个LSTM 隐层。本步骤冻结除了第二个TCN 模块以外的其他全部网络结构,采用步骤4所得强相关数据集对该TCN模块进行微调复训练。
6)步骤6,采用弱相关数据集对LSTM 模块进行微调。本步骤冻结除了第二个LSTM 隐层以外的其他全部网络结构,采用步骤4 所得弱相关数据集对该LSTM模块进行微调复训练。
7)步骤7,采用全部数据微调尾部全连接层。本步骤冻结尾部全连接层以外的其他全部网络结构,采用目标风电场的所有历史样本微调该尾部全连接层,最终得到目标风电场的功率预测模型。
1.2 基于偏差补偿TCN-LSTM的预测模型
源风电场是指区域内与目标风电场高度相似的历史数据充足的风电场。由于源风电场和目标风电场高度相似,因此可以将源风电场的完备预测模型迁移至目标风电场。源风电场的选择参考文献[5]。
1.2.1 TCN-LSTM功率预测模型
本文采用两组TCN残差块和双LSTM 隐层作为TCN-LSTM模型,具体结构如图2所示。
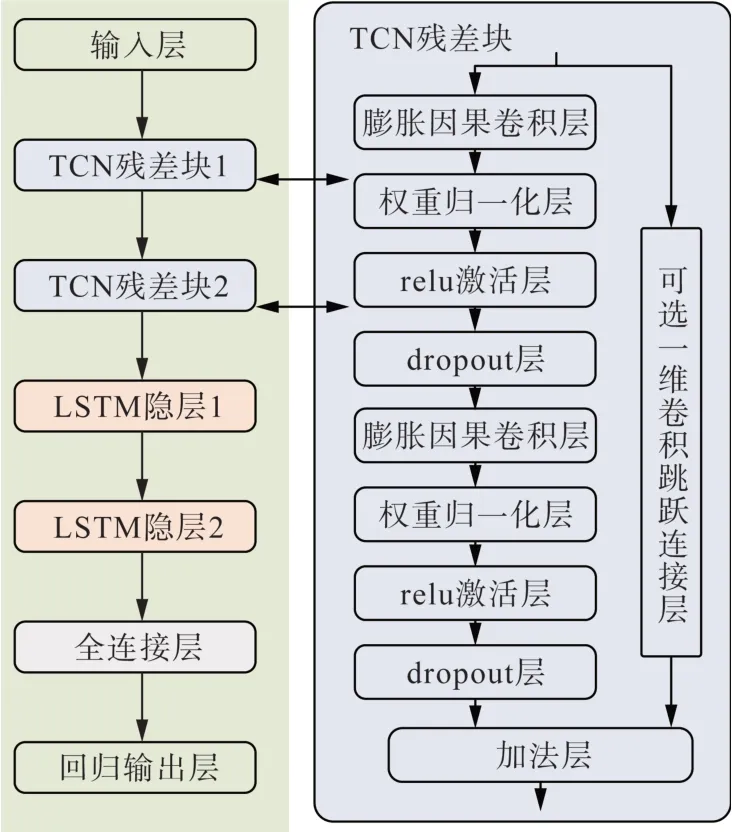
图2 偏差补偿TCN-LSTM模型结构图Fig. 2 Structure of TCN-LSTM model with deviation compensation module
LSTM 是当前的主流时间序列预测模型,在风电功率预测中能有效计及风电序列的时间连续性;TCN则通过膨胀卷积抓取长时间特征,其跨层连接的模型结构能在加快模型训练速度的同时避免原始信息丢失。采用TCN和LSTM 串联结合的方式,能够更有效地从数值天气预报(numerical weather prediction,NWP) 数据中提取高阶时序特征,过滤无用信息,并提高LSTM记忆单元的处理效率。
1.2.2 基于偏差补偿的功率预测方法
偏差补偿方法是指在预测功率时同时预测功率的偏差序列,再将预测功率序列和偏差序列叠加,进而得到更为精准的功率预测结果。偏差补偿模型的训练过程如图3所示,分为3个子步骤。

图3 偏差补偿模型的建模框架图Fig. 3 Framework of modeling with deviation compensation module
1) 子步骤1,采用功率预测模型对数据集B 进行功率预测。采用训练集A 训练的TCN-LSTM 功率预测模型对数据集B 进行功率预测,获取数据集B的预测功率。
2) 子步骤2,计算获取预测偏差序列。预测偏差序列等于真实测量功率减去预测功率。
3) 子步骤3,训练偏差补偿模型。该模型的输入NWP 特征和训练集A 训练的功率预测模型一致,均为空间风资源,模型输出为子步骤2 获取的预测偏差序列。
1.2.3 基于并联融合方法的偏差补偿模型
阶段一源风电场预测建模环节采用结构相同的TCN-LSTM 分别训练功率预测模型和偏差补偿模型。在输入上两个TCN-LSTM 模型一致,均为空间风资源。在输出上两个模型的输出结果直接相加即为最终预测功率。因此可以将两个模型并联融合,构成计及偏差的组合功率预测模型。
本文所提的模型并联融合的方式对于新建风电场具有较高的有效性。对于新建风电场而言,若不进行模型融合,则需要采用两套独立的数据集分别微调功率预测模型和偏差补偿模型。将两个独立的模型视为两个子模块组合成一个网络,进而仅采用一套数据集便可对两个模块同时进行微调,避免了对新建风电场历史数据集的分割,使得偏差补偿方法能被用于新建风电场的功率预测建模。
1.3 基于梯级迁移策略的风电功率预测方法
在获取源风电场完备的计及偏差的组合功率预测模型后,采用目标风电场的少量历史样本对其进行微调,进而将预测模型迁移至目标风电场。
本文采用与源域相关性较高的通用数据和相关性较低的独有数据分别微调复训练功率预测模型的前部和后部特征层。本文所提梯级迁移策略如图4所示。
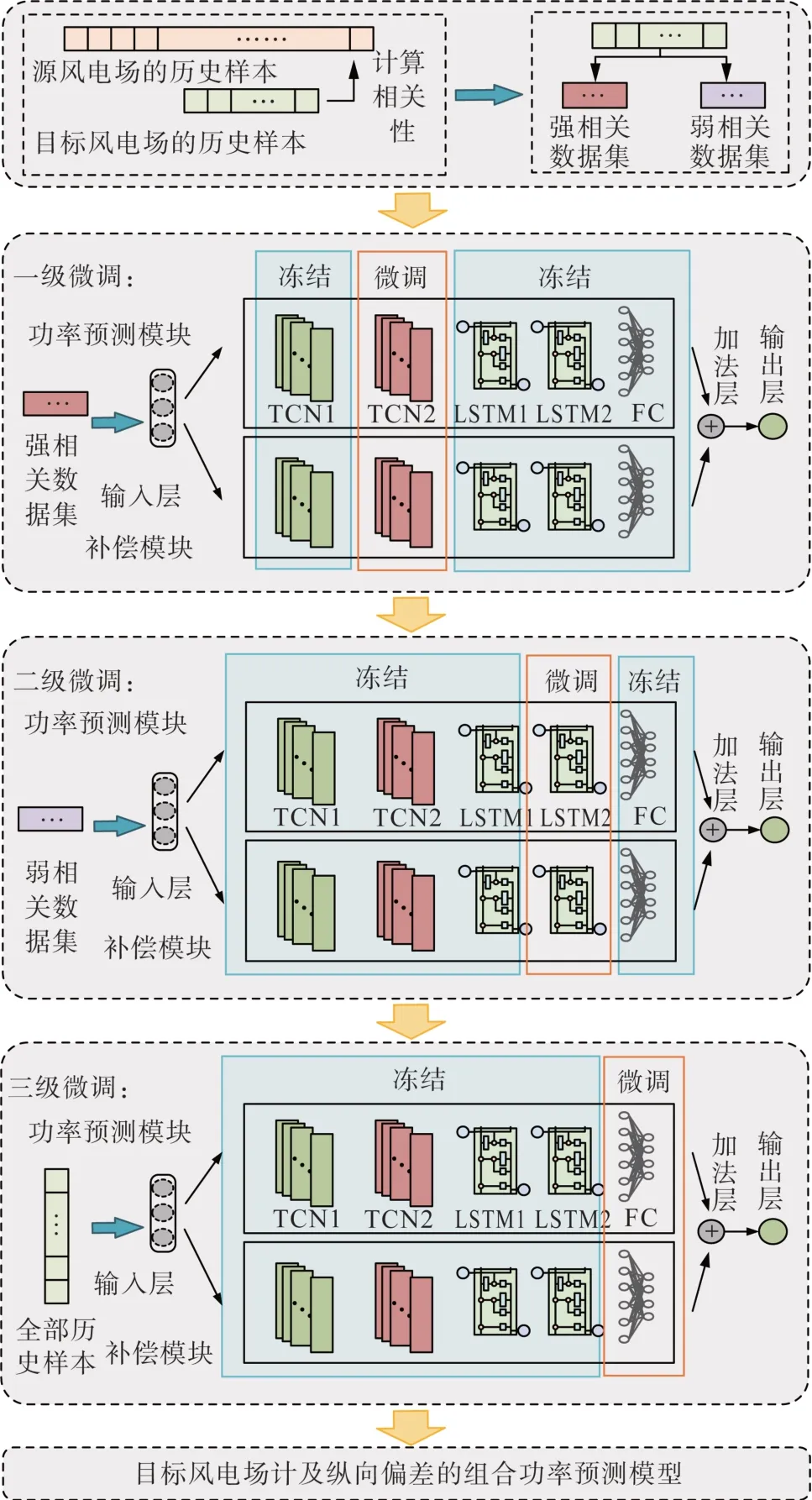
图4 基于梯级迁移策略的短期风电功率预测方法框架图Fig. 4 Framework of short-term wind power prediction method based on step transfer strategy
首先根据目标风电场历史样本与源风电场历史样本之间的相关性将目标风电场的历史样本等分为强相关数据集和弱相关数据集;再进行三级逐步微调,用强相关数据集微调TCN 模块、用弱相关数据集微调LSTM 模块、用全部样本微调尾部全连接层;最终得到迁移后的目标风电场计及偏差的组合功率预测模型。
在对TCN或LSTM 模块进行微调时,冻结位于前部的TCN残差块或LSTM 隐层,只微调位于后部的TCN残差块或LSTM 隐层。这是因为在模型迁移中同种特征模块的浅层隐层被证明主要包含适用于不同数据集的通用特征,而各数据集的独有特征则更多地被深层隐层记载。
2 算例分析
本文选取某地的两个相关风电场进行算例分析,算例分析部分使用数据长度共830 d,时间分辨率为1 h。本文的预测预见期为12 h,采用《Q/GDW 10588—2015》标准[22]推荐的均方根误差(root mean squared error,RMSE,其值用RMSE表示)和平均绝对误差(mean absolute error,MAE,其值用MAE表示)作为风电功率预测的误差评价指标。其计算公式分别如公式(1)—(2)所示。
式中:yi为i时刻的归一化功率预测实际值;ŷi为i时刻的归一化功率预测值;N为测试集中数据样本的数量;ymax为功率最大值,代表归一化过程的作用。
下列每节将先介绍对照组的模型结构、迁移策略,再给出各方法的预测结果。
2.1 目标风电场样本分布
在迁移学习阶段,目标风电场的少量样本需要依照与原风电场的相关性等分为两份。由于源风电场样本与目标风电场样本序列长度不同,在相关性计算部分,动态时间规整(dynamic time warping,DTW)算法将用于计算样本之间的距离[23]。在本节中来自目标风电场的50 d 数据按照NWP 的更新周期12 h 被分成100 个样本,其基于DTW 距离的分布如图5 所示。其中目标风电场样本和源风电场样本间的DTW 距离在8 000~12 500之间。根据梯级迁移策略定义,目标风电场样本中中距离大于9 658 的样本为强相关性样本,其余则为弱相关性样本。
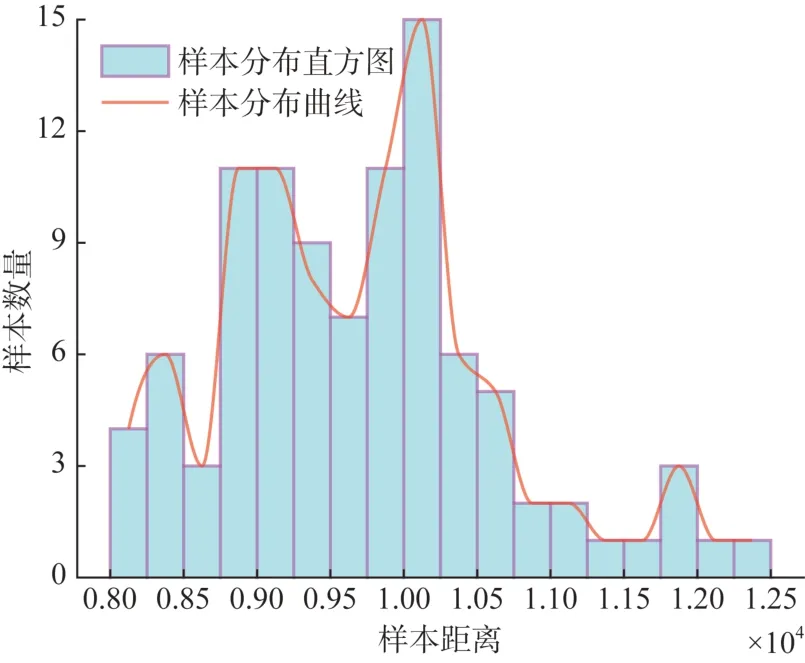
图5 基于DTW距离的目标风电场样本分布Fig. 5 Sample distribution of the target wind farm based on DTW distance
2.2 深度学习方法比较
2.2.1 对照组设置
在本节中用作算例分析的模型参数如表1 所示,本节主要用于选出预测精确度高的深度学习模型,选出的模型在之后的研究中将用作迁移学习的基本模型。
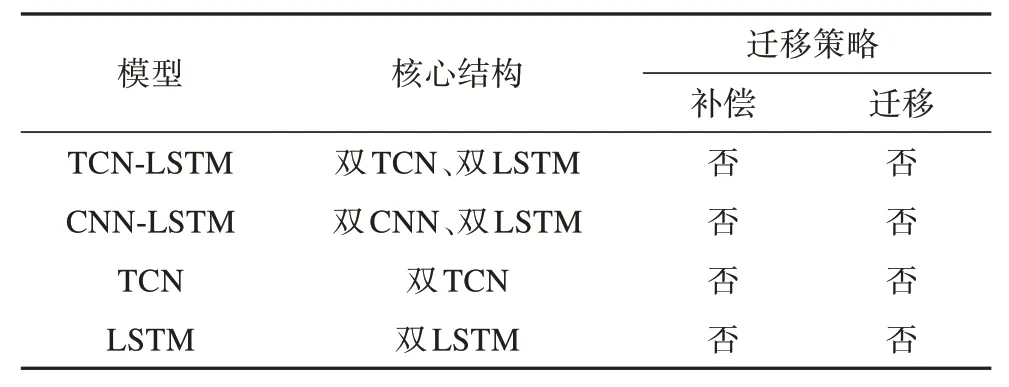
表1 基本深度学习模型参数Tab. 1 Parameters of basic deep learning models
2.2.2 预测误差结果比较
从图6 和表2 中可发现TCN-LSTM 模型的预测RMSE 和MAE 都最小,意味着TCN-LSTM 在特征提取和非线性拟合能力上比其他的对照组神经网络卷积神经网络-LSTM(convolutional neural network-LSTM,CNN-LSTM)、LSTM、TCN 更具优势。其RMSE 误差值相比与传统模型下降0.08%~0.24%。所以在接下来的迁移学习策略算例分析中将采用TCN-LSTM神经网络作为基础模型。
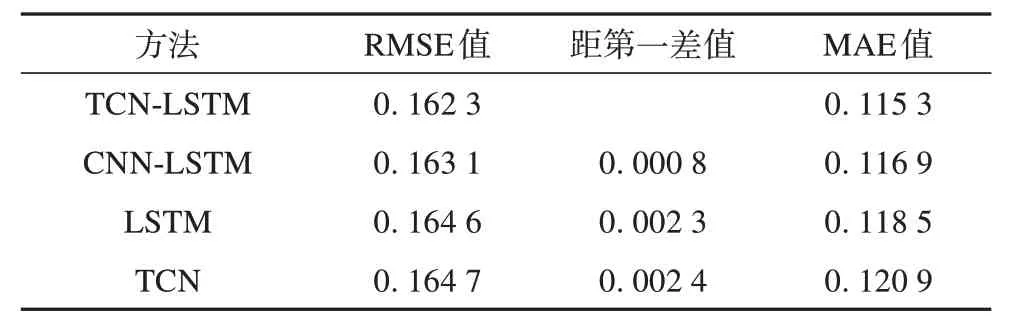
表2 基本深度学习模型直接建模预测误差对比Tab. 2 Comparison of prediction errors in direct modeling of basic deep learning models

图6 基本深度学习模型直接建模预测误差曲线Fig. 6 Prediction error curves by direct modeling of basic deep learning models
2.3 基于偏差补偿模型迁移学习预测结果分析
2.3.1 对照组设置
在本节中用作算例分析的模型参数如表3 所示,本节主要用于通过误差曲线算例比较证明所提的偏差补偿模块在新建风电场迁移学习功率预测中的有效性。

表3 不同迁移学习模型参数Tab. 3 Parameters of deep learning models with different transfer learning strategies
2.3.2 预测误差结果比较
图7 和表4 中可以发现:1) TCN-LSTM 相比于CNN-LSTM 模型在迁移学习中也具有更好的表现。2) 通过迁移学习能够有效提高新建风电场的功率预测精度,例如TCN-LSTM-直接迁移模型相比于TCN-LSTM 模型直接预测进度提升0.84%。3)误差偏差补偿结构能有效地提高风电功率迁移学习的预测精度,例如TCN-LSTM 补偿迁移模型预测精度相比于TCN-LSTM 直接迁移模型,RMSE 预测误差减小了0.21%,CNN-LSTN-补偿迁移模型相比于CNN-LSTM-直接迁移模型RMSE 预测误差下降了0.17%。

表4 基于不同迁移学习模型的预测误差对比Tab. 4 Comparison of prediction errors based on models with different transfer learning models
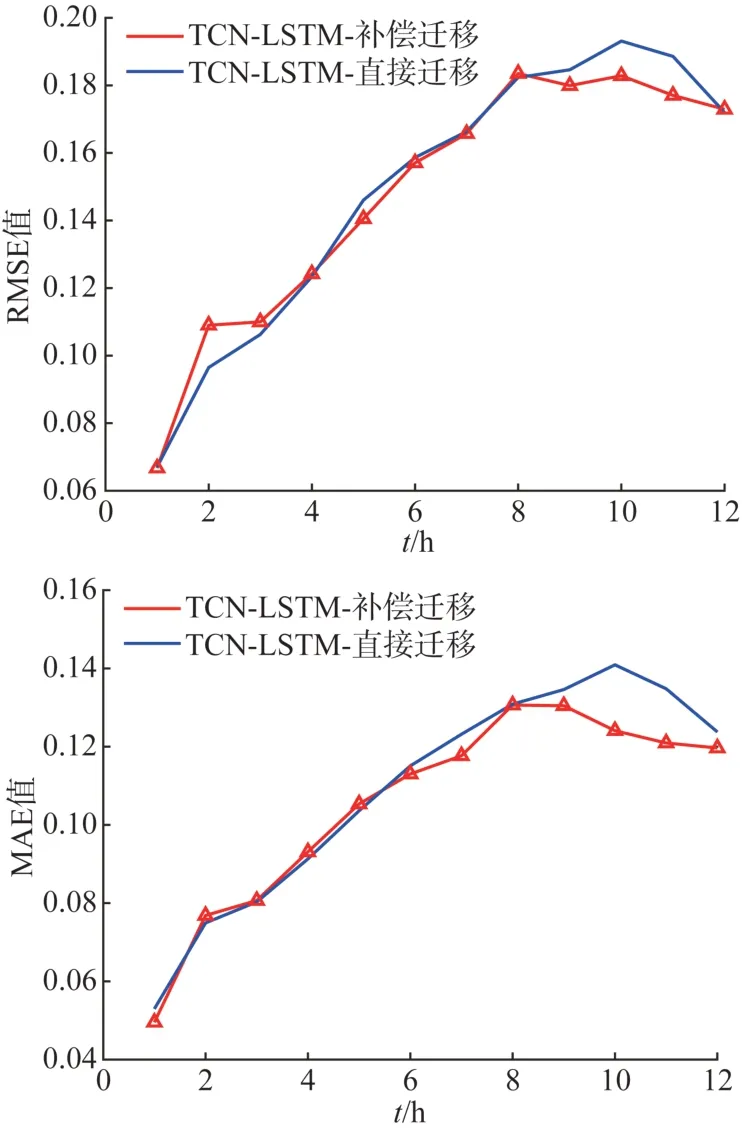
图7 基于不同迁移学习模型的预测误差曲线Fig. 7 Prediction error curves based on models with different transfer learning models
2.4 基于梯级迁移策略的预测功率比较分析
2.4.1 对照组设置
在本节中用作算例分析的模型参数如表5 所示,本节主要用于通过预测功率与实际功率曲线算例比较证明所提的梯级迁移策略在基于TCN-LSTM深度学习模型的新建风电场迁移学习功率预测中的有效性。
2.4.2 预测功率结果比较
从图8 和表6 可以发现:梯级迁移方法相比传统的单步迁移方法能有效提高迁移学习的目标任务特征提取能力,提高预测精度。TCN-LSTM-补偿梯级迁移模型相比于TCN-LSTM-补偿迁移模型RMSE预测误差减小0.18%。

表6 基于不同迁移学习策略的模型预测误差对比Tab. 6 Comparison of prediction errors based on models with different transfer learning strategies
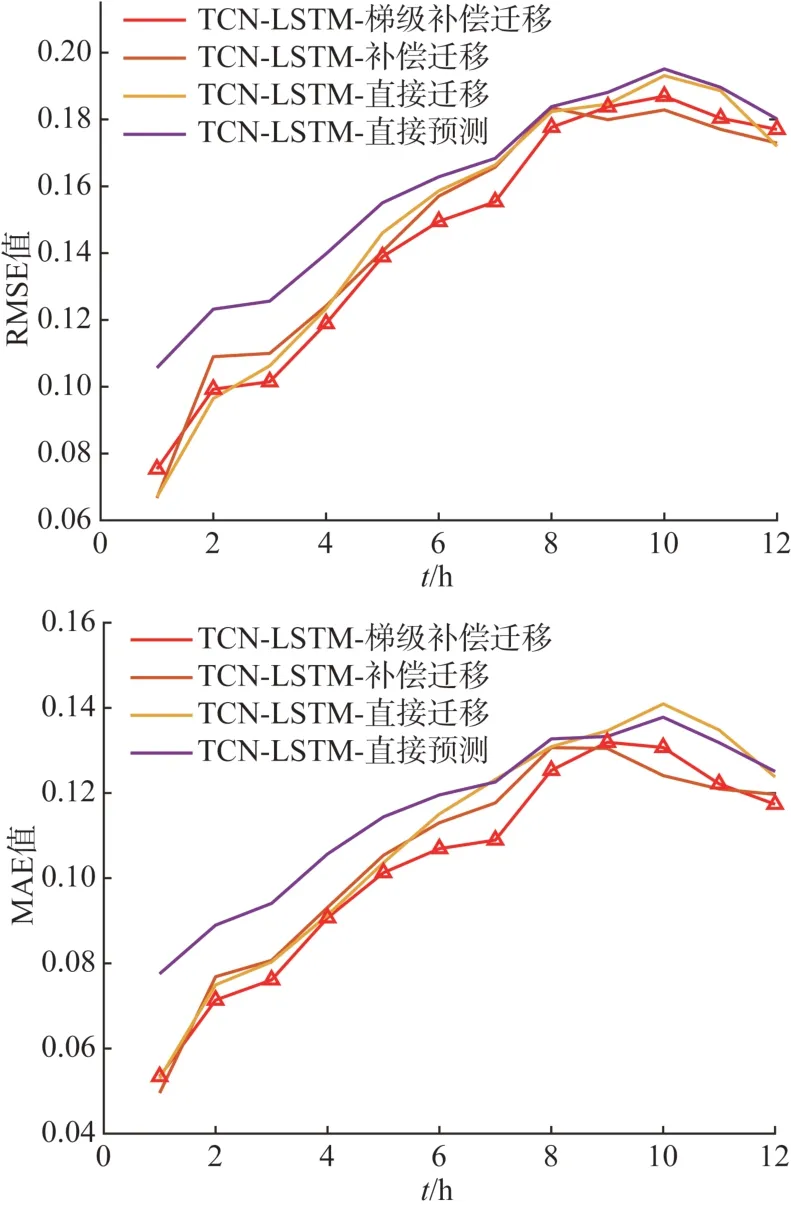
图8 基于不同迁移学习策略的模型预测误差曲线Fig. 8 Prediction error curves based on models with different transfer learning strategies
图9 中(b)、(c)、(d)子图是(a)主图的部分截取放大。从图9 中可以看出采用梯级补偿迁移的模型表现优于采用传统迁移学习方法的模型。通过补偿梯级迁移模型/补偿迁移模型,补偿迁移模型/直接迁移模型两组对照比较,梯级迁移策略和偏差补偿模块的应用都有效地提升了迁移学习预测精度。
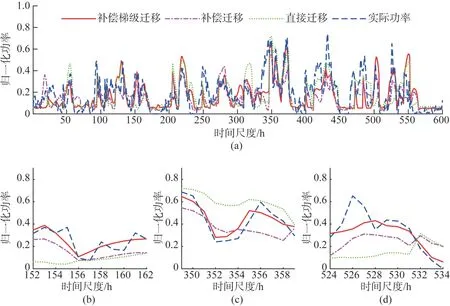
图9 基于TCN-LSTM不同迁移策略的预测功率曲线对比Fig. 9 Comparison of predicted power curves based on TCN-LSTM with different transfer strategies
3 结论
本文提出了基于偏差补偿TCN-LSTM 和梯级迁移策略的短期风电功率预测,通过3 组比较算例验证了所提出方法的有效性。本文的主要结论如下。
1) 本文提出的加入偏差补偿模块以及梯级迁移策略的TCN-LSTM 模型相较基于传统迁移学习策略的模型以及单独建模的方法,其短期风电预测精度有明显的提升。基于偏差补偿TCN-LSTM 和梯级迁移策略的短期风电功率预测模型相比于使用不足数据直接预测的TCN-LSTM、CNN-LSTM、LSTM、TCN 模型在12h 预测中精度分别提高1.23%、1.31%、1.46%、1.47%。
2) 在对新建风电场短期风电功率进行迁移学习预测的过程中,误差补偿模块的加入有效提高了迁移学习预测精度。加入误差补偿模块的TCN-LSTM 和CNN-LSTM 模型相较于单独的同类预测模型可分别提高0.21%,0.17%的短期预测精度。
3) 相较于传统的单步迁移学习方法,本文所提梯级迁移学习策略能够与误差补偿模块共同应用于迁移学习中,并有效提高短期风电功率预测精度。其中TCN-LSTM-补偿梯级迁移模型相比于TCN-LSTM-补偿迁移模型预测精度提高了0.18%。

