基于样本间潜在关系的多变量时间序列分类

唐胜唐, 吴共庆, 台昌杨, 杨 泽, 张 赞

(合肥工业大学 计算机与信息学院,安徽 合肥 230601)

0 引 言

多变量时间序列(multivariate time series,MTS)是通过监测多个指标(变量)收集的具有时间特性的一系列数据。 多变量时间序列分类(multivariate time series classification,MTSC)是将时间序列分类为预定义类别的任务,它是数据挖掘领域中一个重要且具有挑战性的问题,吸引了众多研究者的关注,已广泛应用于医疗保健、运动识别和天气预测[1]等诸多领域。

早期的MTS分类方法大多是基于距离的方法[2]和基于特征的方法[3],它们依赖于从原始MTS数据中提取特征并结合传统分类器进行分类,难以直接处理原始MTS数据,需要大量的领域专业知识和特征工程对数据进行处理。 近年来,基于深度学习的方法[4]在时间序列分类中取得了优异的表现。 其相比于传统的MTS分类方法能够更全面且自主地学习MTS数据中隐藏的丰富的有价值信息,取得更好的分类效果,然而在对MTS数据的关系利用上依旧存在不足。

MTS样本间隐藏了丰富的关系信息。 以医疗领域为例,利用心电图仪器可以对心脏活动进行实时监测并采样,从而获取一系列具有时序关系并且相互联系的MTS数据样本。 医生可以根据这些样本的关系以及相关数据的分析结果对病人病情做出判断。 然而,现有的MTS分类方法通常将MTS样本当作一个单独的个体进行处理,未考虑样本间隐藏的关系信息,难以有效提升分类性能。 同时这些方法构建的分类模型只使用了标记样本的数据进行训练,未能有效利用未标记的样本,在标记的样本较少的数据集上分类性能不佳。

为了更好地捕获MTS数据中的关系信息,一些研究者将MTS数据映射到图空间,通过图神经网络(graph neural network,GNN)挖掘数据中潜在的关系[5-6]。 近年来,图神经网络在许多任务上都取得了优异的表现[7]。 以图卷积网络(graph convolutional network,GCN)为例,它通过图结构扩展信息,引入可以优化的卷积参数对节点的邻居进行卷积操作,使每个节点都能充分利用其邻接节点的特征信息,不但获得了节点更有效的特征表示,而且能将图中未标记节点的特征信息充分利用起来,可以有效地处理节点分类任务。

为了充分挖掘MTS样本间的潜在关系,本文提出一种基于GCN的MTS分类框架,通过挖掘样本间的潜在关系和利用未标记数据来提高分类性能。 为了对样本关系进行建模,本文设计了一种基于样本相似性的关系映射准则构造样本关系图,将时间序列数据映射到图空间来获取样本间潜在关系的特征表示。 在图的构建过程中,图节点包括标记样本和未标记样本,因此,模型可以充分利用未标记样本包含的有价值的信息。 为了获得样本关系图中的多阶邻接样本特征信息,提出使用由多个不同的图卷积层组成的MTS分类模型,通过图结构聚合和更新其t阶相邻样本信息学习图的深层结构表示。 大量实验结果验证了本文提出的分类模型的有效性。 本文的主要贡献概括如下:

1) 提出一种基于图卷积网络的MTS分类框架,能够获取MTS样本的关系信息,进而将其与样本特征信息进行融合生成语义更丰富的多变量时序数据的样本表示。

2) 设计了一种基于样本相似性的关系映射准则,将MTS样本映射到图空间,获取样本间潜在关系的特征表示。

3) 本文在11个数据集上进行了大量实验,并与12种多变量时间序列分类方法进行比较。 实验结果表明,该方法在分类性能方面具有显著优越性。

1 相关工作

本文提出一种新的MTS分类模型,通过对MTS样本进行建模,将样本关系映射到图空间,使用GCN获取样本间潜在关系信息的特征表示用于分类。

1.1 多变量时间序列分类

MTS分类方法可分为基于距离的方法、基于特征的方法、基于模型的方法和基于深度学习的方法4种。

基于距离的方法采用欧几里德距离[8]、短时间序列距离[9]、动态时间规整距离(dynamic time wrapping,DTW)[10-11]及其各种变体[12-13]等利用相似性度量准则计算时间序列之间的相似性,然后根据测试实例与训练实例之间的相似性对测试实例进行分类。 基于特征的方法采用时间序列Shapelets模型[14]、多变量时间序列的符号表示模型[15]和广义多变量Shapelet模型[16]等将时间序列转换为特征向量,从原始MTS数据中提取全局或局部的特征,提供给分类器进行分类。 基于模型的方法采用高斯混合模型[17]、多变量高斯模型[18]和隐马尔可夫模型[19]等使用模型参数表示原始时间序列,根据假设模型对数据建模,通过衡量模型之间的相似度进行分类。

近年来,基于深度学习的方法在时间序列分类领域表现优异。 文献[20-22]引入自动学习特征的理念,通过神经网络中逐层的特征变换,将MTS样本在原始空间上的特征表示映射到一个新特征空间,使用这些新特征能够更容易地实现分类的目的。 与人工构造规则抽取特征、设计模型的方法相比,基于深度学习的方法可以自动地学习特征,提取数据蕴含的丰富信息以提升分类性能。

上述分类方法仅学习序列的特征信息,没有考虑序列间的复杂关系。 鉴于图模型能方便地表示对象之间的关系,本文引入图模型,用于表示序列之间的关系,通过基于图模型的挖掘方法发现序列之间的关系辅助,提升MTS分类性能。

1.2 图卷积网络

随着图神经网络[23]的兴起,基于消息传递[24]、信息传播[25]和图卷积[26]设计的GNN模型已被应用于网络分析和自然语言处理等诸多领域。 图卷积网络[26]和图注意网络[27]等学习有效的消息传递机制,对节点及其邻居节点进行加权求和,通过多层图卷积,聚合多阶节点之间的信息以表达节点的关系信息,利用最后一层卷积得到的节点特征向量执行分类或预测等任务。

已有研究工作探索将图神经网络应用于MTS处理任务。 文献[28]设计一种新的池化层MTPool,与GCN结合,捕获MTS变量之间的隐藏依赖关系和时序信息用于分类。 StemGNN[29]是实现MTS预测的深度学习框架,集成了图傅里叶变换和离散傅里叶变换,以捕获序列间的相关性。 MTGNN[30]结合了图卷积模块和时间卷积模块,捕获MTS变量之间的依赖关系用于MTS预测任务。 这些基于GNN的方法能够有效获取MTS变量之间的依赖关系,在MTS分类和预测等领域取得了较好的效果。

然而,上述方法没有将MTS样本之间的关系用于提升MTS分类任务的精度。 因此,本文探索将样本的关系信息映射到图空间,对MTS样本进行编码,利用GCN的关系获取能力和节点分类能力挖掘样本间潜在的关系信息以提升分类性能。

2 基于图卷积的MTSC模型

本节设计基于图卷积网络挖掘样本间潜在关系的多变量时间序列分类模型(MTSC based on GCN,GMTSC),详细介绍模型的组成以及基于模型的分类算法设计。 MTSC模型如图1所示。

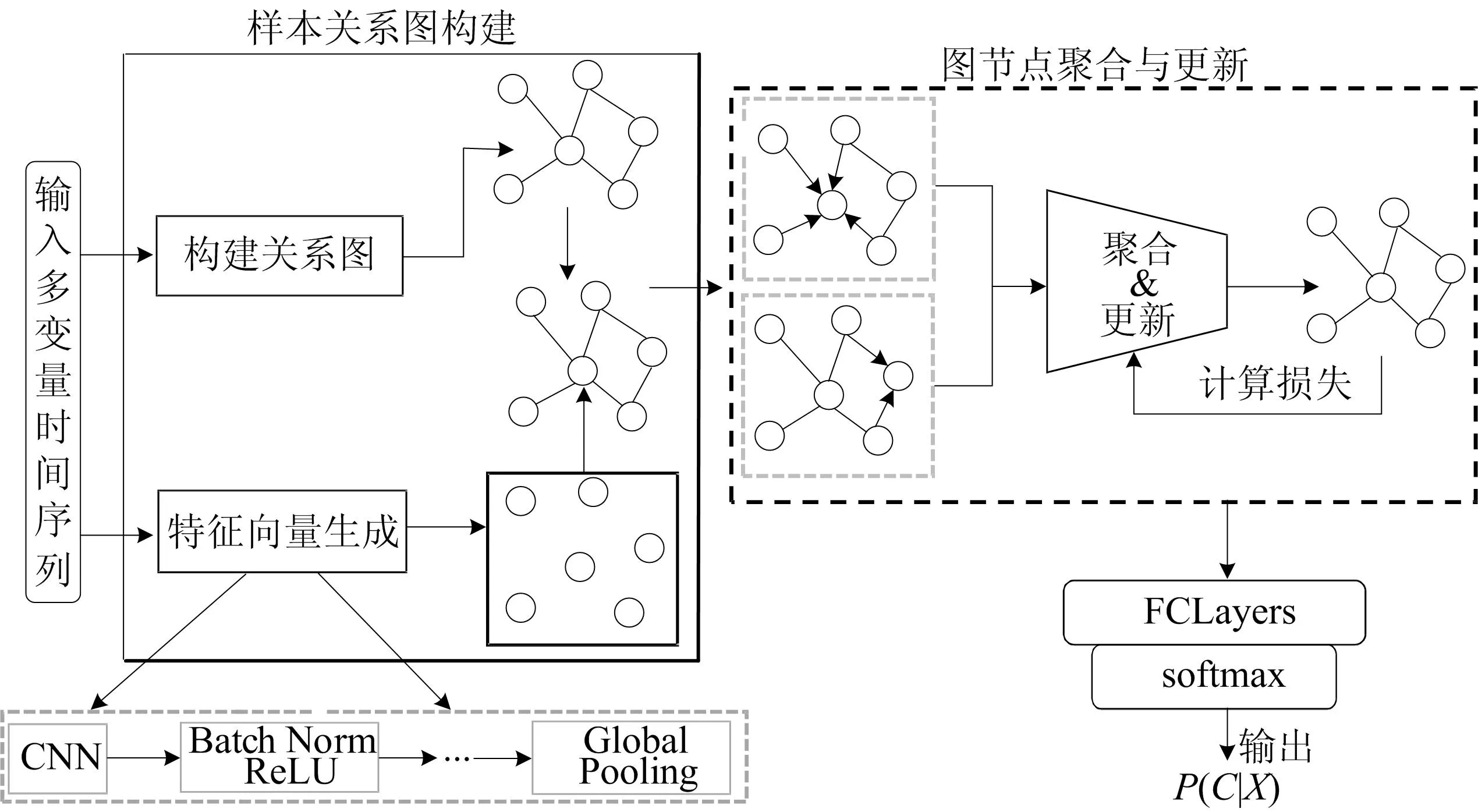
图1 GMTSC模型

2.1 GMTSC模型

直推学习在训练时会同时使用训练集和测试集数据,在训练阶段不使用测试集样本的标签,只在测试阶段使用测试集样本的标签用于性能评估,适合基于图卷积模型的学习。 本文基于直推学习范式设计了一种半监督图卷积模型GMTSC用于多变量时序样本分类。 由图1可知GMTSC包含2个模块:样本关系图构建模块以及图节点聚合与更新模块。 首先,输入原始时间序列样本数据,基于样本相似度量按照直推学习范式对训练集和测试集中的样本统一建图,将样本间的关系信息映射到图空间;然后,利用卷积神经网络对每个样本提取多个时间戳上的特征,映射为样本节点的特征向量,通过图卷积在图空间上挖掘样本间的潜在关系信息用于分类任务,此外通过迭代优化训练样本的预测值,提升模型对样本关系的获取能力,进而将关系信息有效地编码到样本的特征向量上;最后,通过一个线性分类器,将测试样本编码后的特征向量映射为该测试样本的概率向量以预测类别。

2.2 样本关系图构建

使用图卷积挖掘MTS样本之间的潜在关系信息需要预定义的图结构。 本文使用样本建立图的节点,基于样本相似性的映射准则计算样本之间的相似度量,选择每个样本的前k个最相似样本作为邻接节点,构建无向边,为整个MTS数据集构建样本关系图。

在构建无向边时,由于DTW算法能够自动规整时间序列,通过时间轴上的局部缩放,可使2个序列的形态接近以计算相似度。 因此,本文选择DTW算法进行样本的相似度量来寻找邻接节点构建无向边,生成图结构。 对于多变量时间序列样本,基于多维变量计算维度相关的DTW距离DTW,而不是单独面向每个维度进行计算,计算公式为:

DTW(t1,t2)={dis(t1,t2)+min[DTW(t1-1,t2),DTW(t1,t2-1),DTW(t1-1,t2-1)]}1/2

(1)

其中:dis(t1,t2)=(Xi(t1)-Xi(t2))2为MTS数据集任意2个样本Xi的t1时间戳和Xj的t2时间戳相对应的所有变量观察值的局部距离;DTW(t1,t2)为从Xi和Xj的第1个时间戳到Xi的t1时间戳和Xj的t2时间戳的最小累加距离。

关系图节点的数据表示形式为一维特征向量。 然而,根据样本构建的节点对应的原始样本数据是一个二维矩阵。 为了便于GCN对图的操作,需要重建节点的数据,将原始样本数据的二维矩阵映射为对应节点的一维特征向量。 向量映射准则为:① 保留原始数据之间的特征和时序性;② 映射的特征向量符合图卷积网络的输入要求;③ 每个节点特征向量的维数是统一的。

根据上述向量映射准则,设计堆叠卷积神经网络(convolutional neural network,CCN),将节点的原始二维矩阵数据映射为一维特征向量,以图中所有节点的原始样本数据作为输入,使用多个具有不同大小卷积核的卷积神经网络层提取样本中多变量和多时间戳下的特征,通过全局池化将采样的特征映射为一维向量,计算公式为:

(2)

其中:X={X1,X2,…,XN}为原MTS始样本数据的集合;N为数据集中样本数;T、M分别为每个样本的时间戳数和变量数;D为映射生成的特征向量的维度。

2.3 图节点聚合与更新

上述过程通过对样本关系进行建模生成样本关系图,将关系信息映射到图空间。 为了在分类时能充分利用样本间的潜在关系信息,本文基于图卷积模型对样本节点执行聚合和更新操作,将样本在图上多个邻接样本的特征信息结合起来作为样本特征的补足信息,并与样本自身特征融合,将潜在样本关系信息编码到节点特征向量上。 通过不断融合节点的邻接样本信息(潜在样本关系信息)来更新节点自身样本特征,直到模型达到稳定均衡。

单个节点聚合与更新操作计算公式为:

(3)

其中:i∈[1,N],Near(Xi)为样本Xi的邻居样本集合;Vu∈R1×d为Xi的邻居样本的特征向量;Vi′∈R1×d′为Xi经过邻域聚合与更新后的特征向量;d为样本原始特征长度;d′为模型预设置的输出特征维度;W∈Rd×d′为节点聚合其相邻节点特征后进行线性变换的权重矩阵;σ为激活函数。

对所有节点的聚合与更新操作计算公式为:

(4)

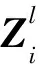
(5)

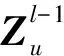
2.4 GMTSC算法

本节给出基于直推学习范式下的多变量时间序列分类算法GMTSC,算法描述如下:

输入:时间序列训练集样本和标签、测试集样本和迭代次数epoch。

输出:测试集样本的预测标签。

1) 使用训练集和测试集样本构建样本关系图;

2) 将原始MTS样本数据映射为图节点的一维特征向量;

3) 输入样本关系图到图卷积模块;

4) 迭代epoch次,每次迭代中在每层图卷积层都对样本节点的特征进行聚合和更新,得到更新后的特征向量;

5) 使用算法对训练集样本标签进行预测;

6) 根据训练集样本的预测标签与真实标签计算图卷积模块的损失;

7) 根据算法的损失优化算法的权重参数,返回步骤4)进入下一次迭代;

8) 迭代结束,根据训练好的GMTSC算法对测试集的标签进行预测;

9) 返回测试集的预测标签。

算法步骤1)～步骤3)根据式(1)～式(2)构建样本关系图,输入到图卷积模块;步骤4)～步骤7)是算法的训练过程。 首先算法步骤4)基于样本关系图,使用多层图卷积捕获图中样本节点的关系信息并编码到节点的特征向量上,然后通过一层全连接层对训练样本的标签进行预测,计算公式为:

(6)

算法步骤5)～步骤7)每次迭代利用训练样本的预测标签与它们的真实标签对比计算算法的损失,将其作为反馈信息来指导算法中权重参数的更新。 交叉熵可以用来计算学习算法分布与训练分布之间的差异,一般情况下可以收敛得到更好的局部极小值点,本文使用交叉熵函数计算算法的损失,计算公式为:

(7)

算法步骤8)～步骤9)是算法的分类过程,在算法训练结束后,通过式(6)对图中测试样本的标签进行预测以完成分类。

3 GMTSC的实验设计及结果分析

本文使用分类精度、平均精度和每种算法能达到最佳精度的数据集数量作为实验的评价指标,迭代次数epoch为100,实验环境为Intel (R) Core(TM) i7-9800x CPU@3.80 GHz CPU、32 GiB RAM、Windows 10 Pro 64,开发平台为Python 3.7。

3.1 数据集

本文从UEA&UCR时间序列数据集网站中选择了5个类别共11个公开MTS数据集,见表1所列。

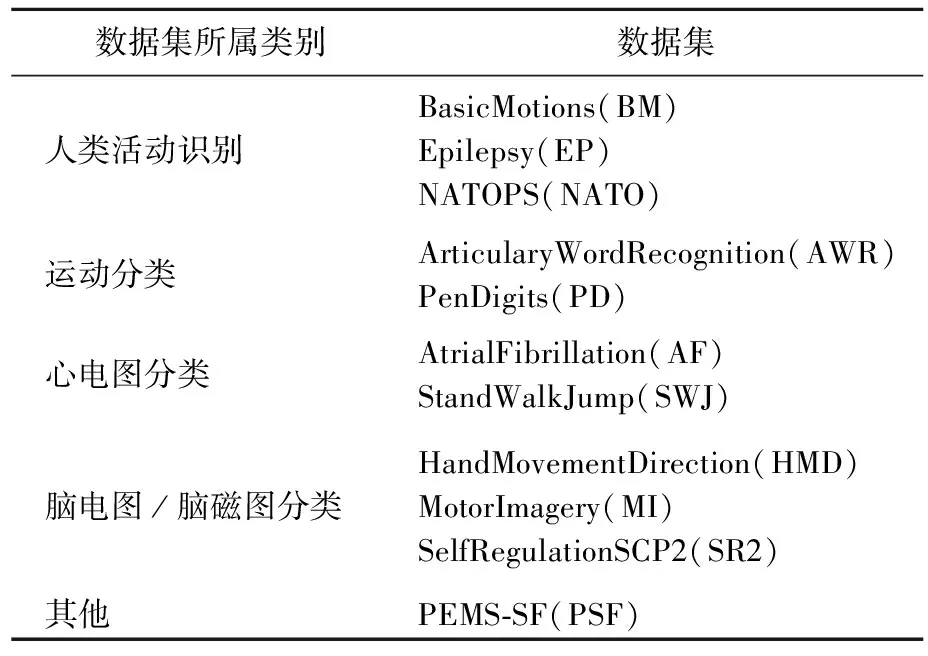
表1 数据集所属的类别

实验数据集的基本信息见表2所列。 数据集由不同应用程序收集的真实多变量时间序列数据组成,包括人类活动识别、运动分类、音频频谱分类等,包含了广泛样本、维度和序列长度的真实多变量时序数据。

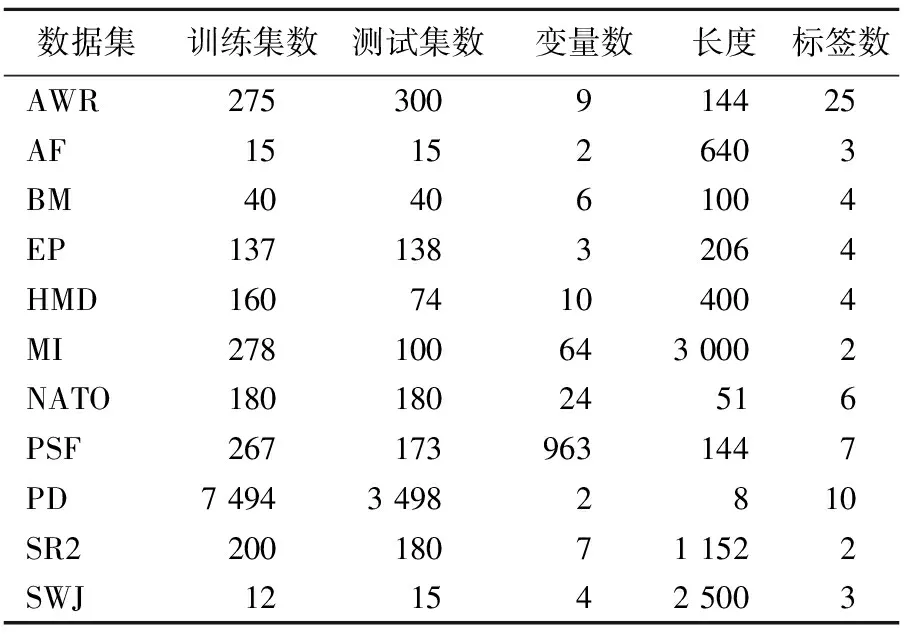
表2 实验数据集及其基本信息

数据集中的变量数量从轨迹分类数据集中的2维变量到交通流分类任务中的963维变量不等,时间序列长度在8～3 000之间,样本数量在27～10 992之间,样本数据的分布是随机的,具有代表性。

3.2 对比算法

本文对比算法选择在MTSC领域的12种代表性分类算法,包括9种监督分类算法和3种半监督分类算法。

9种监督分类算法如下:

1) 1NN-ED[8]。 使用欧氏距离作为MTS之间的距离度量的最近邻分类器。

2) 1NN-DTW-I[31]。 最近邻分类器中分别计算MTS每个维度的DTW距离,并将其总和作为分类依据。

3) 1NN-DTW-D[31]。 将每个时间戳对应的多个变量的观测值视为一个点,在最近邻分类器计算距离时,对齐过程与传统的DTW算法相同。

4) WEASEL-MUSE[32]。 使用多个窗口长度来构建一个大的特征空间,然后使用卡方检验来确定最相关的特征并将其输入到逻辑回归模型中。

5) MLSTM-FCN[4]。 将全卷积网络模型与LSTM进行结合,同时向全卷积模块中添加了压缩模块和激励模块。

6) Tapnet[20]。 设计了一个将时间序列的维度重构为组的随机组置换方法,从多变量时间序列数据中学习低维特征,利用标记样本和未标记样本设计了一个注意原型网络,有效解决了缺少标记样本训练模型的问题。

7) 1NN-ED(norm)。 1NN-ED在分类前对输入数据进行的归一化操作。

8) 1NN-DTW-I(norm)。 1NN-DTW-I在分类前对输入数据进行的归一化操作。

9) 1NN-DTW-D(norm)。 1NN-DTW-D在分类前对输入数据进行的归一化操作。

3种半监督分类算法如下:

1) 1NN-DTW-D[33]。 使用基于距离的最近邻分类器构建时间序列半监督学习算法。

2) MTL[34]。 利用已建立的多任务学习算法,将模型预测作为次要任务与主分类任务一起优化。

3) Semi-Tapnet[20]。 Tapnet的注意原型网络利用未标记数据将模型扩展到半监督模式,应用于MTS半监督分类。

3.3 实验结果与分析

3.3.1 监督分类算法的实验结果比较

GMTSC与9种监督分类算法的分类精度、平均精度和能达到最佳精度的数据集数量(获胜数)见表3所列。

表3 GMTSC和9种MTS分类算法在11个数据集上的分类精度

从表3可以看出,GMTSC不仅在8个数据集上取得了最佳分类精度,而且平均分类精度也达到了最佳(0.775),远远优于分类精度次佳的Tapnet(0.716)。 这说明GMTSC通过将样本关系映射到图空间,利用图卷积挖掘样本间的潜在关系信息用于分类,为样本提供了更多的可区分特征。 相比之下,几种传统的基于距离的方法平均分类精度只在0.650左右,这是由于它们只简单利用了与测试样本最相似的训练集样本进行分类,没有深入考虑样本间潜在的关系信息。

基于特征的分类方法和深度学习的分类方法虽然在EP和PSF等数据集中也获得了最佳的分类精度,但在11个数据集上的平均精度也只在0.68左右,远远不及GMTSC。 这是由于它们在处理每个MTS样本时,仅将其作为独立个体进行特征提取,很少考虑使用其他相似的样本特征信息来丰富自身特征表示。

此外,在AF和SWJ只有少量标记样本的数据集上, GMTSC也取得了最佳分类精度,说明GMTSC充分利用了未标记样本包含的有价值的信息,有效提升了分类性能。

本文还给出了GMTSC与9种对比算法分类性能差异的临界差值图,如图2所示,具有最佳排名的分类算法位于图中右侧。 从图2可以看出GMTSC的平均排名最高。 根据 Friedman test,若算法性能相同,则它们的平均排名也相等,图2表明GMTSC以及其他9种对比方法的性能都不相同。 使用 Nemenyi test做进一步区分,设定显著性水平α=0.05,计算出平均排名差别的临界值域(critical difference, CD),若2个算法的平均排名之差超出了该阈值说明2个算法性能有差异,图2表明GMTSC在性能上显著优于大部分方法。

图2 GMTSC与9种对比算法分类性能差异的邻接差值图

3.3.2 半监督分类算法的实验结果比较

本文选择了4个属于不同领域的数据集来评估GMTSC在不同的监督水平下的分类效果,并与1NN-DTW-D、Semi-Tapnet和MTL这3种代表性半监督分类算法进行对比。 在划分数据集时,按照0.1～1.0递增比例r,选取训练集中每个类别对应该比例的样本数标记样本进行训练,剩下的样本作为无标记样本,保证选取的训练集样本包含所有的类别。

GMTSC与其他3种算法在这4个数据集下的分类精度如图3所示。

图3 GMTSC与3种半监督分类算法的实验结果

从图3可以看出,GMTSC在分类精度上明显优于对比算法,尤其在AWR数据集上,GMTSC在只有0.1带标记样本集上训练时分类精度能达到0.983,明显优于Semi-Tapnet(0.790)、MTL(0.835)和1NN-DTW-D(0.400)。

由图3可知,随着划分比例的增加,GMTSC的分类性能稳定提升,而Semi-Tapnet、MTL和1NN-DTW-D的分类性能整体变化趋势不稳定,尤其是基于距离的半监督算法1NN-DTW-D极易受到单MTS样本(噪声数据)的影响。

上述结果表明,即使只有较少的标记样本,GMTSC通过对样本间关系信息的挖掘以及利用未标记样本,在MTS半监督分类任务中具有较好的分类性能。

4 结 论

本文提出了GMTSC算法并用于MTS分类,设计了一种挖掘时间序列样本间潜在关系的图卷积模型,该模型能捕获映射到图空间的样本间关系信息用于MTS分类,通过对样本节点执行聚合和更新操作,将潜在样本关系信息编码到节点特征向量更新节点自身特征以提高分类精度。 在11个数据集上与12种代表性算法进行对比,实验结果表明GMTSC在MTS分类任务上具有优越的性能。 未来可进一步从以下2个方面开展研究:

1) 在样本关系图构建方面,探索设计一种新的构图规则,解决基于DTW算法构建样本关系图时间复杂度过高的问题,并能够很好地衡量时间序列之间的距离以处理时间序列不等长的问题,从而提高建图质量。

2) 在模型结构设计方面,改进图卷积网络,在对节点进行聚合和更新时,将与节点相连的边的特征信息附加到节点的特征向量上一起计算,以捕获更充分的样本间关系信息,以期进一步提高MTS分类性能。